MobileNet v3 中 引用的Squeeze-and-Excite是怎么回事

MobileNet v3 中 引用的Squeeze-and-Excite是怎么回事

是什么

Squeeze-and-Excite 对应的论文是Squeeze-and-Excitation Networks
Sequeeze-and-Excitation是什么
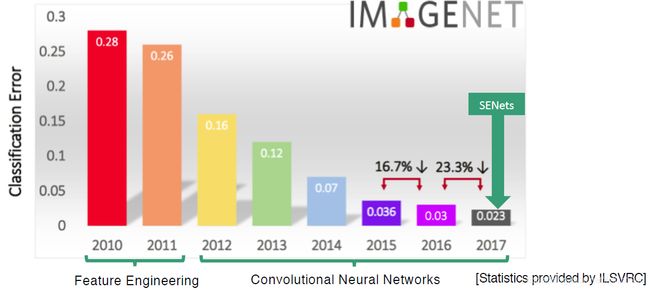
Sequeeze-and-Excitation(SE) Block是一个子模块，可以嵌到其他的模型中，作者采用SENet Block和ResNeXt结合在ILSVRC 2017的分类项目中得了第一。

层次结构

Sequeeze-and-Excitation的层次结构如下
1、AdaptiveAvgPool2d
2、Linear
3、ReLU
4、Linear
5、Sigmoid
先拆成两部分Squeeze部分和Excitation部分
Squeeze部分就是AdaptiveAvgPool2d
Excitation部分就是2到5
先是 squeeze 很形象的词挤压柠檬汁，挤压使用的函数是AdaptiveAvgPool2d(1)
就像以管理小白兔的方式挤压柠檬汁，挤压柠檬汁之后就是Excitation，汁少（ 特征少）的那就大棒伺候，汁多（特征多）的给胡萝卜，特征少的抑制它，特征多的就多多关注它。
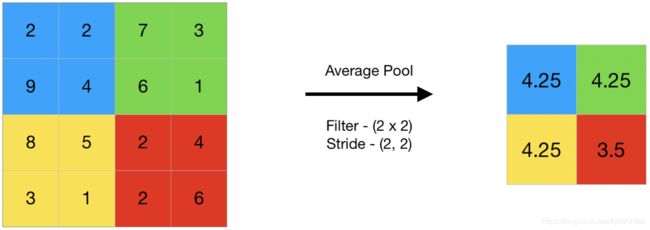
先看Pool，术语叫 池化，意思是合并 多个数要变一个数

pool是怎么多个数变一个数呢？可以是算平均Avg，也可以是取最大
下面是每4个数变一个数
最大的方式
同样的表示

平均的方式

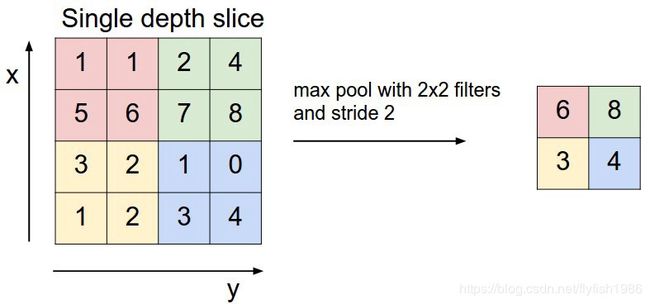
因为输出大小是可以变化的所以叫在最前面加个Adaptive
这里我们想要做的全局平均池化 global average pooling，所以AdaptiveAvgPool2d需要加参数1,就是AdaptiveAvgPool2d(1)
AdaptiveAvgPool2d(1)干了什么事呢？看下图一目了然


有avg就有max

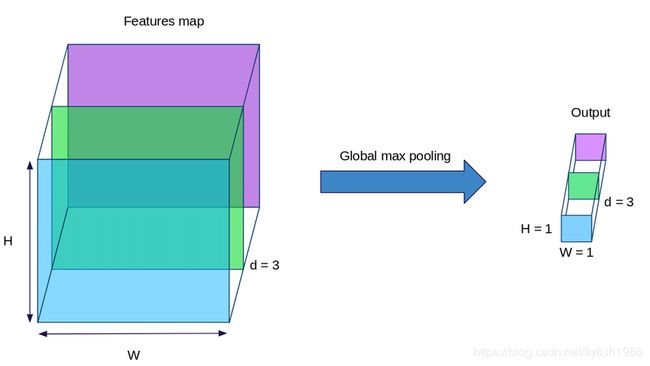
3通道（channel）的一张图片，经过AdaptiveAvgPool2d(1)，输出都是1×1×channel
全局平均池化（global average pooling）概念即使不知道经过了上面的图片展示，意思就明白了

global average pooling 来源论文《Network In Network》
我们提出了另一种称为全局平均池的策略来取代CNN中传统的全连接层（we propose another strategy called global average pooling to replace the traditional fully connected layers in CNN.）
Network in Network工作使用global average pooling来取代了最后的全连接层。

PyTorch代码实现SE块

以下简称SE块

class SELayer(nn.Module):
    def __init__(self, channel, reduction=16):
        super(SELayer, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.fc = nn.Sequential(
            nn.Linear(channel, channel // reduction, bias=False),
            nn.ReLU(inplace=True),
            nn.Linear(channel // reduction, channel, bias=False),
            nn.Sigmoid()
        )

    def forward(self, x):
        b, c, _, _ = x.size()
        y = self.avg_pool(x).view(b, c)
        y = self.fc(y).view(b, c, 1, 1)
        return x * y.expand_as(x)

dummy_input = torch.randn(1,30, 300, 300)
print(SELayer(30)(dummy_input))

SELayer(
(avg_pool): AdaptiveAvgPool2d(output_size=1)
(fc): Sequential(
(0): Linear(in_features=30, out_features=1, bias=False)
(1): ReLU(inplace)
(2): Linear(in_features=1, out_features=30, bias=False)
(3): Sigmoid()
)
)

// 的解释
// 表示 floor division
返回商的整数部分（Returns the integral part of the quotient）

>>> 5.0 / 2
2.5
>>> 5.0 // 2
2.0

分别输出forward中的y的shape是
torch.Size([1, 30])
torch.Size([1, 30, 1, 1])

AdaptiveAvgPool2d的其他使用方式
torch.nn.AdaptiveAvgPool2d(output_size)

对于任何输入尺寸，输出的大小为H x W.输出feature的数量等于输入plane的数量。

# target output size of 5x7
m = nn.AdaptiveAvgPool2d((5,7))
input = torch.randn(1, 64, 8, 9)
output = m(input)
print(output.shape)
# target output size of 7x7 (square)
m = nn.AdaptiveAvgPool2d(7)
input = torch.randn(1, 64, 10, 9)
output = m(input)
print(output.shape)
# target output size of 10x7
m = nn.AdaptiveMaxPool2d((None, 7))
input = torch.randn(1, 64, 10, 9)
output = m(input)
print(output.shape)

输出结果

torch.Size([1, 64, 5, 7])
torch.Size([1, 64, 7, 7])
torch.Size([1, 64, 10, 7])

expand_as的解释
Expand this tensor to the same size as other. self.expand_as(other) is equivalent to self.expand(other.size()).

将此张量扩展到与其他张量相同的大小
self.expand_as(other) = self.expand(other.size()).

把h-sigmoid加入到SE块的实现

class h_sigmoid(nn.Module):
    def __init__(self, inplace=True):
        super(h_sigmoid, self).__init__()
        self.inplace = inplace

    def forward(self, x):
        return F.relu6(x + 3., inplace=self.inplace) / 6.

class SELayer2(nn.Module):
    def __init__(self, channel, reduction=16):
        super(SELayer2, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.fc = nn.Sequential(
            nn.Linear(channel, channel // reduction),
            nn.ReLU(inplace=True),
            nn.Linear(channel // reduction, channel),
            h_sigmoid()
        )

    def forward(self, x):
        batch, channels, height, width = x.size()
        out = self.avg_pool(x).view(batch, channels)
        out = self.fc(out)
        out = out.view(batch, channels, 1, 1)

        return out * x



print(SELayer2(30))

输出

SELayer2(
  (avg_pool): AdaptiveAvgPool2d(output_size=1)
  (fc): Sequential(
    (0): Linear(in_features=30, out_features=1, bias=True)
    (1): ReLU(inplace)
    (2): Linear(in_features=1, out_features=30, bias=True)
    (3): h_sigmoid()
  )
)

如果按照论文的表达方式就是这样的

Squeeze-and-Excitation

整体图是这样的
下面这个图片来源于PPT，可以在下面的链接下载

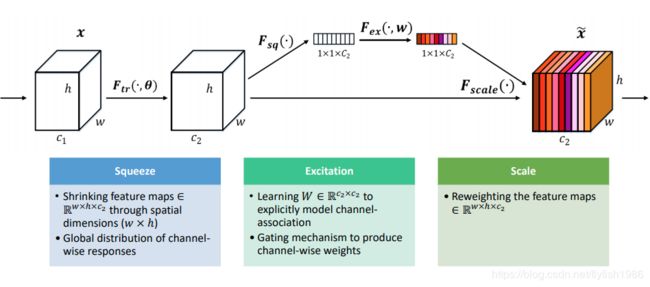
先拆成两部分Squeeze部分和Excitation部分
Squeeze之前的部分

$${\mathbf{F}}_{tr}:\mathbf{x}\to \mathbf{U},\mathbf{x}\in {\mathbb{R}}^{w^{\prime }\times H^{\prime }\times C^{\prime }},\mathbf{U}\in {\mathbb{R}}^{W\times H\times C}$$

tr这里是transformation
transformation F tr mapping an input X to feature maps U
相当于我们自己的一些卷积代码
式子虽多，就是卷积操作，卷积操作如下
$${\mathbf{u}}_c={\mathbf{v}}_c\ast \mathbf{X}=\sum _{s=1}^{C^{\prime }}{\mathbf{v}}_c^s\ast {\mathbf{x}}^s$$

$${\mathbf{v}}_c=\left[{\mathbf{v}}_c^1,{\mathbf{v}}_c^2,\dots ,{\mathbf{v}}_c^{C^{\prime }}\right]$$

$$\mathbf{X}=\left[{\mathbf{x}}^1,{\mathbf{x}}^2,\dots ,{\mathbf{x}}^{C^{\prime }}\right]$$

$${\mathbf{u}}_c\in {\mathbb{R}}^{H\times W}$$

**看论文里Sequeeze的介绍 **

式子

$$z_c={\mathbf{F}}_{sq}\left({\mathbf{u}}_c\right)=\frac{1}{H\times W}\sum _{i=1}^H\sum _{j=1}^W{u}_c(i,j)$$

Sequeeze是压缩，它压缩的是什么呢
X经过卷积输出是U （X-conv-U）
U经过什么得到 结果A，大小是 1 × 1 × C (这里A是为了理解，假设得到一个中间结果)

U -》Global Average Pooling-》A
U -》Fsq(.) -》A
U -》 Squeeze -》A
上面的U怎么得到A的过程就是Squeeze
Squeeze，图上的Fsq(.)，论文里的Global Average Pooling 都是指代一个意思

Squeeze的式子是这样的
$$z_c={\mathbf{F}}_{sq}\left({\mathbf{u}}_c\right)=\frac{1}{H\times W}\sum _{i=1}^H\sum _{j=1}^W{u}_c(i,j)$$

这里的代码是 nn.AdaptiveAvgPool2d

压缩的是 spatial dimension ( H × W )
H × W 就有了名字叫 空间维度 （spatial dimension）

Squeeze 采用了求平均的方式，将空间维度（spatial dimension上）所有点的都计算为一个值

Excitation是什么

用两个全连接来实现
一个全连接把C个通道压缩成了$\frac{C}{r}$个通道 ，这个全连接之后是ReLU，
第二个全连接再恢复回C个通道，这个全连接之后是Sigmoid，
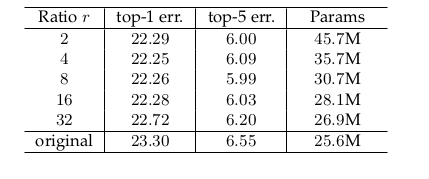
r是指压缩的比例，In the aggregate, when setting the reduction ratio
r to 16。
r是个超参数,默认是16，16平衡的好

接着Squeeze得到的A
A-》FC-》ReLU （通道数由C变成了$\frac{C}{r}$）
-》FC-》Sigmoid (通道数由 $\frac{C}{r}$ 变成了C)

$$\mathbf{s}={\mathbf{F}}_{ex}(\mathbf{z},\mathbf{W})=\sigma (g(\mathbf{z},\mathbf{W}))=\sigma \left({\mathbf{W}}_2\delta \left({\mathbf{W}}_1\mathbf{z}\right)\right)$$

$$\sigma :\text{ 表示 Sigmoid; }\delta :\text{ 表示 ReLU; }$$

输出结果是

$${\mathbf{x}}_c={\mathbf{F}}_{\text{ scale }}\left({\mathbf{u}}_c,s_c\right)=s_c{\mathbf{u}}_c$$

用1×1的卷积替换全连接层的代码实现

代码已经实现了，这里还有个“但是”，“但是”之后就是代码的另一种写法
看大神Yann LeCun说的话

Yann LeCun

In Convolutional Nets, there is no such thing as “fully-connected layers”. There are only convolution layers with 1x1 convolution kernels and a full connection table. It’s a too-rarely-understood fact that ConvNets don’t need to have a fixed-size input. You can train them on inputs that happen to produce a single output vector (with no spatial extent), and then apply them to larger images. Instead of a single output vector, you then get a spatial map of output vectors. Each vector sees input windows at different locations on the input. In that scenario, the “fully connected layers” really act as 1x1 convolutions.

我们是可以用1×1的卷积替换全连接层的
那么代码就变成了下面的样子

class SeModule(nn.Module):
    def __init__(self, in_size, reduction=4):
        super(SeModule, self).__init__()
        self.se = nn.Sequential(
            nn.AdaptiveAvgPool2d(1),
            nn.Conv2d(in_size, in_size // reduction, kernel_size=1, stride=1, padding=0, bias=False),
            nn.BatchNorm2d(in_size // reduction),
            nn.ReLU(inplace=True),
            nn.Conv2d(in_size // reduction, in_size, kernel_size=1, stride=1, padding=0, bias=False),
            nn.BatchNorm2d(in_size),
            hsigmoid()
        )

    def forward(self, x):
        return x * self.se(x)

在MobileNet v3中reduction=4，SENet原论文的设计是reduction=16
we replace them all to fixed to be 1/4 of the number
of channels in expansion layer.
因为是个SENet是个子模块就可以嵌入到其他网络结构中例如

参考
Network In Network

Global Average Pooling Layers for Object Localization

Deep Learning Cage Match: Max Pooling vs Convolutions

1D Global average pooling

2D Global average pooling

CNN | Introduction to Pooling Layer

1x1 Convolutions Demystified

How to understand the mlpconv layer in the NIN network

Squeeze-and-Excitation Networks

SENet 的PPT

Searching for MobileNetV3

原作者的代码实现

Squeeze-and-Excitation_Networks论文