简单实现哈夫曼树的建立、编码与解码

哈夫曼树建立、编码、解码

1、哈夫曼树的建立

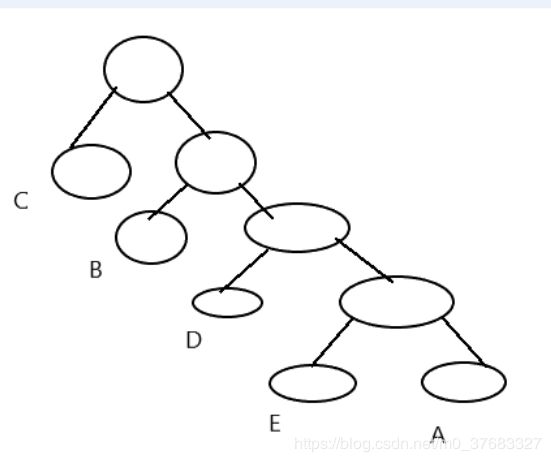
Huffman树是根据元素的权重建立的，权重较小的离根结点较远，而权重较大的离根结点较近，从而使得整个Huffman树有着最小的带权路径长度。Huffman树的具体特性请参考《数据结构》一书或者是其他博客。

首先给出Huffman树的结点类：

public class HuffmanNode {
	int weight;
	char c;
	HuffmanNode left;
	HuffmanNode right;
	//HuffmanNode parent;
	boolean isMin = false;
	
	// 构造函数
	public HuffmanNode (int weight, char c) {
		this.weight = weight;
		this.c = c;
		this.left = null;
		this.right = null;
		//this.parent = null;
		this.isMin = false;
	}
}

解释说明：weight表示权重，c表示元素，类型是char，left，right，parent分别表示当前结点的左右孩子以及其父结点，isMin是boolean的，用于在构造Huffman树时判断是否已经将其作为最小值处理过。

给出Huffman树的构造方法

public HuffmanNode buildHuffmanTree (HuffmanNode[] nodeList, int length) {
		int len = nodeList.length - length;
		HuffmanNode parentNode = null;
		for (int i = 0; i <= len-1; i++) {
			int j;
			HuffmanNode min1 = new HuffmanNode(7500, '#');
			HuffmanNode min2 = new HuffmanNode(7500, '#');
			
			// 得到权重最小的两个Huffman结点
			int isMin1Flag = -1;
			int isMin2Flag = -1;
			for (int k = 0; k < length+i; k++) {
				if (!nodeList[k].isMin) {
					if ((nodeList[k].weight < min1.weight)) {
						min2 = min1;
						isMin2Flag = isMin1Flag;
						min1 = nodeList[k];
						isMin1Flag = k;
					} else if ((nodeList[k].weight <= min2.weight)) {
						min2 = nodeList[k];
						isMin2Flag = k;
					}
				}
			}
			
			nodeList[isMin1Flag].isMin = true;
			nodeList[isMin2Flag].isMin = true;
			
			// 创建新的结点并添加到Huffman数组的末尾
			parentNode = new HuffmanNode(min1.weight + min2.weight, '#');
			
			//min1.parent = parentNode;
			//min2.parent = parentNode;
			
			parentNode.left = min1;
			parentNode.right = min2;
			
			nodeList[length+i] = parentNode;
		}
		return parentNode;
	}

解释说明：函数的参数是Huffman结点类型的数组，同时也给出了Huffman树的叶子结点的个数。可以根据叶子结点的个数确定需要建立多少个结点。根据公式：Huffman树的结点个数=（叶子结点个数*2-1）。由此可以知道需要进行多少次循环。
每一次循环都会选取当前结点中最小的两个结点进行合并。选择数组中最小的两个元素的实现程序在上一篇博客中已经介绍了，有需要的请参考博客：https://blog.csdn.net/m0_37683327/article/details/102208966
选择最小的两个结点之后将其isMin标记为true，意思是已经处理过了，之后就不再处理了！
创建一个新结点，权重是最小的两个结点权重之和，并将其设置为这两个最小结点的父结点。之后将父结点加入到Huffman结点数组的末尾。返回最后一次构建的父结点，该父结点就是整个Huffman树的根结点。
在这里，为了验证构建的是否正确，简单写了一个层次遍历，遍历一遍Huffman树。

层次遍历方法：

public void levelTraversal () {
		if (root == null) {
			return;
		}
		
		Queue queue = new LinkedList();
		
		HuffmanNode current = root;
		
		queue.offer(current);
		while (!queue.isEmpty()) {
			current = queue.poll();
			System.out.print(current.weight + " ");
			
			if (current.left != null) {
				queue.offer(current.left);
			}
			
			if (current.right != null) {
				queue.offer(current.right);
			}
		}
	}

2、哈夫曼树编码

基本思路：对于给定的字符串，依次处理其中的每一个字符，在建立成功的Huffman树中搜索，找到字符后将从根结点到该字符结点的序列输出，在这里，我设置的是向左为0，向右为1。
这里的搜索策略近似于非递归后序遍历，访问孩子结点之后再去访问父结点，这里的编码就是在此基础上修改完成的。

public String getEncodeofCharacter (char c) {
		Stack stack1 = new Stack();
		Stack stack2 = new Stack();
		String code = "";
		// 使用类似于非递归后序遍历哈夫曼树
		if (root == null) {
			return "";
		}
		
		HuffmanNode current = root;
		HuffmanNode preNode = null;
		
		while (current != null) {
			stack2.add(current);
			stack1.add("0");
			current = current.left;
		}
		
		// 多入栈了一个0,弹出栈
		stack1.pop();
		
		// 开始判断哈夫曼树结点中的字符是否是我们要查找的
		while (!stack2.isEmpty()) {
			current = stack2.pop();
			
			if (current.right == null || current.right == preNode) {
				preNode = current;
				
				// 如果找到了我们需要编码的字符就退出循环
				if (current.c == c) {
					break;
				} else {
				// 如果当前结点不是我们需要的字符，就弹出序列的栈顶元素
					stack1.pop();
				}
			} else {
			// 如果弹出的结点还不能访问，那么将其再次压入栈中，访问其右子树
				stack2.add(current);
				
				current = current.right;
				stack1.add("1");
				stack2.add(current);
				
				while (current.left != null) {
					stack2.add(current.left);
					stack1.add("0");
					current = current.left;
				}
			}
		}
		
		// 退出while循环，每次弹出栈都放在当前编码的前面
		// 这里也可以使用一个栈stack3，将stack1的元素弹出的同时压入到stack3中，最后弹出stack3栈顶元素即可。
		while (!stack1.isEmpty()) {
			code = stack1.pop() + code;
		}
		
		return code;
	}

3、哈夫曼树解码

基本思路：根据给定的编码，遍历Huffman树，当前编码值为0向左进入左子树，是1进入右子树，并且每次都要判断是否达到叶子结点。
如果达到叶子结点，输出叶子的元素值，并设置下一次解码重新从根结点开始；如果没有达到叶子结点，那么就继续按照上面的规则前进，直到到达叶子结点为止。

Huffman树解码代码：

public String getDecodeofCode (String encode) {
		String decode = "";
		int len = encode.length();
		int i = 0;
		
		HuffmanNode current = root;
		
		while (i < len) {
			if (encode.charAt(i) == '1') {
				current = current.right;
			} else {
				current = current.left;
			}
			
			if (current.left == null && current.right == null) {
				decode += current.c + "";
				current = root;
			} 
			
			i++;
		}
		return decode;
	}

4、测试用例及运行结果

public static void main(String[] args) {
		HuffmanTree ht = new HuffmanTree();
		HuffmanNode[] nodeList = new HuffmanNode[9];

		nodeList[0] = new HuffmanNode(5, 'E');
		nodeList[1] = new HuffmanNode(15, 'D');
		nodeList[2] = new HuffmanNode(40, 'C');
		nodeList[3] = new HuffmanNode(30, 'B');
		nodeList[4] = new HuffmanNode(10, 'A');

		// 前面五个元素已经初始化了，在这里把后面的元素初始化
		for (int i = 5; i < nodeList.length; i++) {
			nodeList[i] = new HuffmanNode(-1, '#');
		}

		ht.root = ht.buildHuffmanTree(nodeList, 5);
		ht.levelTraversal();

		//利用哈夫曼树进行编码
		String test = "EADBCBD";
		String Encode = ht.getEncodeofString(test);
		System.out.println("\n" + Encode);

		//利用哈夫曼树进行解码
		System.out.println(ht.getDecodeofCode(Encode));
}

运行结果：

100 40 60 30 30 15 15 5 10 
1110111111010010110
EADBCBD

构造的哈夫曼树是一个如下图的二叉树：