机器学习之逻辑回归实战---信用卡欺诈检测
一、一个完整机器学习项目的流程
1 抽象成数学问题
明确问题是进行机器学习的第一步。机器学习的训练过程通常都是一件非常耗时的事情,胡乱尝试时间成本是非常高的。
这里的抽象成数学问题,指的我们明确我们可以获得什么样的数据,目标是一个分类还是回归或者是聚类的问题,如果都不是的话,如果划归为其中的某类问题。
2 获取数据
数据决定了机器学习结果的上限,而算法只是尽可能逼近这个上限。
数据要有代表性,否则必然会过拟合。
而且对于分类问题,数据偏斜不能过于严重,不同类别的数据数量不要有数个数量级的差距。
而且还要对数据的量级有一个评估,多少个样本,多少个特征,可以估算出其对内存的消耗程度,判断训练过程中内存是否能够放得下。如果放不下就得考虑改进算法或者使用一些降维的技巧了。如果数据量实在太大,那就要考虑分布式了。
3 特征预处理与特征选择
良好的数据要能够提取出良好的特征才能真正发挥效力。
特征预处理、数据清洗是很关键的步骤,往往能够使得算法的效果和性能得到显著提高。归一化、离散化、因子化、缺失值处理、去除共线性等,数据挖掘过程中很多时间就花在它们上面。这些工作简单可复制,收益稳定可预期,是机器学习的基础必备步骤。
筛选出显著特征、摒弃非显著特征,需要机器学习工程师反复理解业务。这对很多结果有决定性的影响。特征选择好了,非常简单的算法也能得出良好、稳定的结果。这需要运用特征有效性分析的相关技术,如相关系数、卡方检验、平均互信息、条件熵、后验概率、逻辑回归权重等方法。
4 训练模型与调优
直到这一步才用到我们上面说的算法进行训练。现在很多算法都能够封装成黑盒供人使用。但是真正考验水平的是调整这些算法的(超)参数,使得结果变得更加优良。这需要我们对算法的原理有深入的理解。理解越深入,就越能发现问题的症结,提出良好的调优方案。
5 模型诊断
如何确定模型调优的方向与思路呢?这就需要对模型进行诊断的技术。
过拟合、欠拟合 判断是模型诊断中至关重要的一步。常见的方法如交叉验证,绘制学习曲线等。过拟合的基本调优思路是增加数据量,降低模型复杂度。欠拟合的基本调优思路是提高特征数量和质量,增加模型复杂度。
误差分析 也是机器学习至关重要的步骤。通过观察误差样本,全面分析误差产生误差的原因:是参数的问题还是算法选择的问题,是特征的问题还是数据本身的问题……
诊断后的模型需要进行调优,调优后的新模型需要重新进行诊断,这是一个反复迭代不断逼近的过程,需要不断地尝试, 进而达到最优状态。
6 模型融合
一般来说,模型融合后都能使得效果有一定提升。而且效果很好。
工程上,主要提升算法准确度的方法是分别在模型的前端(特征清洗和预处理,不同的采样模式)与后端(模型融合)上下功夫。因为他们比较标准可复制,效果比较稳定。而直接调参的工作不会很多,毕竟大量数据训练起来太慢了,而且效果难以保证。
7.上线运行
这一部分内容主要跟工程实现的相关性比较大。工程上是结果导向,模型在线上运行的效果直接决定模型的成败。 不单纯包括其准确程度、误差等情况,还包括其运行的速度(时间复杂度)、资源消耗程度(空间复杂度)、稳定性是否可接受。
这些工作流程主要是工程实践上总结出的一些经验。并不是每个项目都包含完整的一个流程。这里的部分只是一个指导性的说明,只有大家自己多实践,多积累项目经验,才会有自己更深刻的认识。
二、信用卡欺诈检测
1、抽象成数学问题
所谓信用卡欺诈检测就是对给定的一次交易进行判定其是否是一次欺诈交易,结果只有两种,即是被欺诈交易或者是正常的交易,所以我们的目的就是进行二分类,所以对于信用卡欺诈检测分为二分类问题。
2、获取数据
此处,数据已经提供好了:
3、特征处理与特征选择
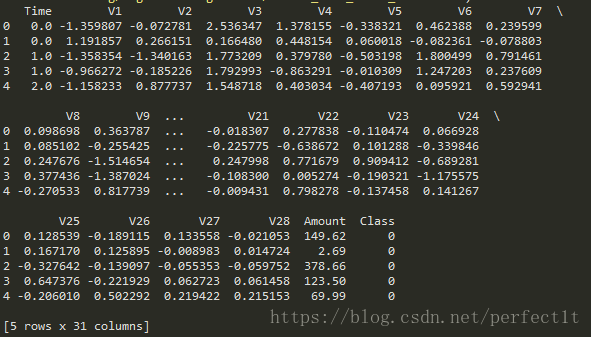
首先我们对第二步的数据进行查看分析,因数据较大,此处只看其前5个的数据,如下所示:
从上图中,我们看出来:从V1到V28,每列的数据的波动幅度不大,即都在-1点多到正2左右,而Amount列的数据却浮动很大,即从几到300多,那么我们就需要对其进行一个预处理,即对Amount列的数据进行标准化处理,让其均值为0,方差为1,因为机器学习很容易存在偏好,即偏向于大的数据。同时,我们还知道,对于Time列(特征)对我们进行预测没有任何的影响,所以我们将把其Drop掉。我们又在原来的基础上添加了Amount列的标准化之后的数据进去,所以把Amount列的数据Drop掉。
最后把处理好的数据的特征和标签分开,X代表特征集,而y表示标签集。代码:
def loadDataSet(filename):
'''
函数说明:读取数据
参数:
filename :数据文件名
返回:data :数据集
'''
data = pd.read_csv(filename)
print(data.head()) # 显示前5个样本
return data
def plotDataSet(data):
'''
函数说明:图形显示正反样本的个数
参数:data:数据集
'''
# 对class列的值的个数进行统计,即此处为统计1和0的各自出现的次数
count_classes = pd.value_counts(data["Class"], sort=True).sort_index()
count_classes.plot(kind = "bar") # 使用pd自带的画图函数数据进行可视化,采用条形图
plt.title("Fraud class histogram")
plt.xlabel("Class")
plt.ylabel("frequency")
print(count_classes)
def dataPreProcess(data):
'''
函数说明:数据预处理
参数:data:原数据集
返回:
data :预处理之后的整个数据集
X :特征集
y : 标签集
注:一般来说,我们的数据集中会存在缺失值,还应进行缺失值处理,
但该数据集已经是进行过处理的数据集,没有缺失值,所以不用进行缺失值处理
'''
# 对data中特征Amount的值进行标准化处理,均值为0,方差为1,并添加到data中
data["normalAmount"] = StandardScaler().fit_transform(data["Amount"].values.reshape(-1, 1))
# axis=1,表示对列进行操作,即drop(丢掉)Time和Amount两个特征
data = data.drop(["Time", "Amount"], axis=1)
print(data.head()) # 查看是否标准化和drop成功
X = data.iloc[:, data.columns != "Class"] # 取出特征集
y = data.iloc[:, data.columns == "Class"] # 取出标签集
return data, X, y4 训练模型与调优
一般对于数据,如果存在类别不平衡,则进行类别平衡处理,为什么要进行处理呢?是因为许多模型的输出类别是基于阈值的,例如逻辑回归中小于0.5的为反例,大于则为正例。在数据不平衡时,默认的阈值会导致模型输出倾向与类别数据多的类别。因此可以在实际应用中,解决办法包括:
- 调整分类阈值,使得更倾向与类别少的数据;
- 选择合适的评估标准,比如ROC、recall或者F1,而不是准确度(accuracy);
- 过采样法(sampling):来处理不平横的问题。分为欠采样(undersampling)和过采样(oversampling)两种,
最常用的方法有欠采样和过采样。关于欠采样和过采样处理类型不平衡问题,以下是几点经验:
- 采样方法一般比直接调整阀值的效果要好;
- 使用采样方法(过采样和欠采样)一般可以提升模型的泛化能力,但有一定的过拟合风险,应搭配使用正则化模型;
- 过采样的效果比较稳定,作为升级版的过采样方法,SMOTE也是不错的处理方式,大部分时候和过采样的效果类似;
- 过采样大部分时候比欠采样效果好,但很难一概而论那种方法最好,还是需要根据数据的特性(如分布)具体讨论;
- 和采样法配合使用的模型最好可以很好的处理过拟合问题。
在此,我们尝试下采样方法,与SMOTE过采样方法。
下采样方法:
def subSampled(data):
'''
函数说明:
对数据进行下采样处理
参数:
data : 数据集
返回:
under_sample_data :下采样后得到的整个数据集
X_undersample :下采样后得到的特征集
y_undersample :下采样后得到的标签集
'''
# 获取标签中为1的长度/个数
number_records_fraud = len(data[data.Class == 1]) # data的类型为DataFrame类型
# 获取标签中为1的下标,并把列表转成array类型
fraud_indices = np.array(data[data.Class == 1].index)
# 获取标签中为0的下标(正常交易),并把列表转成array类型
normal_indices = data[data.Class == 0].index
# 采用下采样(欠采样)方式处理数据,从正常的数据下标中选取不正常个数的下标
# 即从正常数据(多)中随机抽取n个下标,使得正常的数据与不正常的数据的样本数相等
random_normal_indices = np.random.choice(normal_indices, number_records_fraud,
replace = False)
random_normal_indices =np.array(random_normal_indices) # 转成Array数组
# 把两个数据集的下标合并成一个
under_sample_indices = np.concatenate([fraud_indices, random_normal_indices])
# 抽取出下采样后的数据集,并分成特征集和标签集
under_sample_data = data.iloc[under_sample_indices, :]
X_undersample = under_sample_data.iloc[:, under_sample_data.columns != "Class"]
y_undersample = under_sample_data.iloc[:, under_sample_data.columns == "Class"]
# 打印正常以及别欺诈的数据的比重以及总数据的样本数
# print("Percentage of normal transactions: ", len(under_sample_data[under_sample_data.Class == 0])/len(under_sample_data))
# print("Percentage of fraud transactions: ", len(under_sample_data[under_sample_data.Class == 1])/len(under_sample_data))
# print("Total number of transactions in resampled data: ", len(under_sample_data))
return under_sample_data, X_undersample, y_undersample把数据集进行切分,使其分成训练集和测试集:
def dataSegmentation(X, y, test_size = 0.3):
'''
函数说明 :
对数据进行切分,分成train和test两部分
参数:
X : 需要切分特征集
y : 需要切分标签集
test_size : test数据的大小,默认0.3
返回:
X_train : 切分后得到的用于训练的特征集
X_test : 切分后得到的用于测试的特征集
y_train : 切分后得到的用于训练的标签集
y_test : 切分后得到的用于测试的标签集
'''
# 对整个数据集进行train : test = 7 : 3
# 调用sklearn.cross_validation的train_test_split模块
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size = test_size,
random_state = 0)
# 打印切分后的数据的长度,以及总长
# print("Number transactions train dataset: ", len(X_train))
# print("Number transactions test dataset: ", len(X_test))
# print("Total number of transactions: ", len(X_train)+len(X_test))
return X_train, X_test, y_train, y_test在此例中使用Recall(召回率)评估模型,计算公式为: Recall = TP / (TP + FN) ;召回率 = 真正 / (真正 + 错假 = 原数据的正的个数):
# Recall = TP / (TP + FN) 召回率 = 真正 / (真正 + 错假 = 原数据的正的个数)
def printing_Kfold_scores(x_train_data, y_train_data,
k=5, c_para_list = [0.01, 0.1, 1, 10, 100]):
'''
函数说明:
进行k折交叉验证,并找出提供c参数中最优的值
参数:
x_train_data : 用于训练的特征集
y_train_data : 用于训练的标签集
k : 折数,默认5折
c_para_list : 超参数C的可选值列表, 默认为[0.01, 0.1, 1, 10, 100]
返回:
best_c : 最优的超参数c
'''
# 对数据进行分层
fold = KFold(len(y_train_data), k, shuffle=False)
# 不同的c超参数值,C用在正则化项
c_para_range = c_para_list
results_table = pd.DataFrame(index = range(len(c_para_range), 2),
columns = ['C_parameter', 'Mean recall score'])
results_table["C_parameter"] = c_para_range # 把超参数c的列表加入到C_parameter列中
# the k-fold will give 2 list: train_indices = indices[0], test_indices = indices[1]
j = 0
for c_param in c_para_range:
print("------------------------------------")
print("C parameter: ", c_param)
print("------------------------------------")
print("")
recall_accs = []
# 进行k折交叉验证
for iteration, indices in enumerate(fold, start=1):
# 实例化一个logistics regression 模型,采用l1正则化
lr = LogisticRegression(C=c_param, penalty='l1')
# Use the training data to fit the model, In this case, we use the
# portion of the fold to train the model with indices[0]. We the
# predict on the assigned as the 'test cross validation' with indices[1]
lr.fit(x_train_data.iloc[indices[0], :],
y_train_data.iloc[indices[0], :].values.ravel()) # .ravel()表示扁平化,变成向量
# Predict values using the test indices in the training data
# 用训练集中的验证部分进行预测
y_pred_undersample = lr.predict(x_train_data.iloc[indices[1], :].values)
# Calcuate the recall score and append it to a list for recall scores
# representing the current c_parameter
recall_acc = recall_score(y_train_data.iloc[indices[1], :].values,
y_pred_undersample)
recall_accs.append(recall_acc)
print("Iteration ", iteration, ": recall score = ", recall_acc)
# the mean value of those recall scores is the metric we want to
# save and get hold of.
results_table.loc[j, 'Mean recall score'] = np.mean(recall_accs)
j += 1 # 对当前的超参数c做完k折交叉验证,j增1
print("")
#打印当前c值的k折交叉验证的recall(召回率)值的平均值
print("Mean recall score ", np.mean(recall_accs))
print("")
'''
The main problem:
1) the type of "mean recall score" is object, you can't use "idxmax()" to calculate the value
2) you should change "mean recall score" from "object " to "float"
3) you can use apply(pd.to_numeric, errors = 'coerce', axis = 0) to do such things.
'''
# 获取最优的c值
new = results_table.columns[results_table.dtypes.eq(object)] #get the object column of the best_c
results_table[new] = results_table[new].apply(pd.to_numeric, errors = 'coerce', axis=0) # change the type of object best_c
best_c = results_table.loc[results_table["Mean recall score"].idxmax()]["C_parameter"]
#Finally, We can check which C parameter is the best amongst the chosen.
print('********************************************************************************')
print("Best model to choose from scross validation is with C parameter = ", best_c)
print('********************************************************************************')
return best_c混淆矩阵可以让我们直观的看出召回率的情况,绘画混淆矩阵的函数如下:
def plot_confusion_matrix(cnf_matrix, classes, title="Confusion matrix", cmap=plt.cm.Blues):
'''
函数说明:This function prints and plosts the confusion matrix.
打印和画混淆矩阵
参数:
cnf_matrix :需要绘画的混淆矩阵
classes : 类别(一般list类型)
title : 图形名称,默认为"Confusion matrix"
cmap :颜色映射默认为plt.cm.Blues
返回:
无
'''
plt.imshow(cnf_matrix, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
'''
plt.xticks([-1,0,1],['-1','0','1']) #第一个:对应X轴上的值,第二个:显示的文字
'''
plt.xticks(tick_marks, classes, rotation=0) # rotation:旋转
plt.yticks(tick_marks, classes)
thresh = cnf_matrix.max() / 2
for i,j in itertools.product(range(cnf_matrix.shape[0]), range(cnf_matrix.shape[1])):
plt.text(j, i, cnf_matrix[i, j],
horizontalalignment='center',
color='white' if cnf_matrix[i, j] > thresh else 'black')
'''
补充知识点:https://matplotlib.org/api/pyplot_api.html
matplotlib.pyplot.text(x, y, s, fontdict=None, withdash=False, **kwargs)
x, y:表示坐标;
s:字符串文本;
fontdict:字典,可选;
kwargs:
fontsize=12,
horizontalalignment=‘center’、ha=’cener’
verticalalignment=’center’、va=’center’
fig.text()(fig = plt.figure(…))
ax.text() (ax = plt.subplot(…))
'''
plt.tight_layout()
plt.ylabel("True label")
plt.xlabel("Predicted label")data = loadDataSet("creditcard.csv") # 加载数据
plotDataSet(data) # 图形显示数据
# 由数据图可知,我们发现数据出现极度的类型不平衡
# 一般对于这种情况,可以进行下采样和过采样处理,使得数据重新达到平衡
data, X, y = dataPreProcess(data) # 对数据进行预处理
# 下采样方法:
under_sample_data, X_underSample, y_underSample = subSampled(data)
# 对整个数据集进行切分:train : test = 7:3
X_train, X_test, y_train, y_test = dataSegmentation(X, y, test_size = 0.3)
# 对整个数据集进行切分:train : test = 7:3
X_under_train, X_under_test, \
y_under_train, y_under_test = dataSegmentation(X_underSample, y_underSample, test_size = 0.3)
###########################################################################
# 进行交叉验证选择最优的C参数,在下采样数据下
best_c = printing_Kfold_scores(X_under_train, y_under_train, 5, [0.01, 0.1, 1, 10, 100])
# 构建基于最优c参数的lLogistics Regression Model
lr = LogisticRegression(C=best_c, penalty='l1')
lr.fit(X_under_train, y_under_train.values.ravel()) # 训练模型
y_pred_under = lr.predict(X_under_test.values) # 用训练好模型对测试进行预测
# Compute confusion matrix,计算混淆矩阵
cnf_matrix = confusion_matrix(y_under_test, y_pred_under)
# 作用:确定浮点数字、数组、和numpy对象的显示形式。
np.set_printoptions(precision=2) # 精度为小数点后4位
print("Recall metric in the testing dataset: ",
cnf_matrix[1, 1] / (cnf_matrix[1,0] + cnf_matrix[1, 1]))
# plot non-normalized confusion matix
class_name = [0, 1]
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_name, title="Confusion matrix -- under data")
plt.show()
# 对整个完整数据的测试部分进行预测
y_pred_all = lr.predict(X_test.values) # 用训练好模型对测试进行预测
# Compute confusion matrix,计算混淆矩阵
cnf_matrix = confusion_matrix(y_test, y_pred_all)
# 打印召回率
print("Recall metric in the testing dataset: ",
cnf_matrix[1, 1] / (cnf_matrix[1,0] + cnf_matrix[1, 1]))
# plot non-normalized confusion matix
class_name = [0, 1]
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_name, title="Confusion matrix -- all data")
plt.show()
###########################################################################
############################ 不做下采样处理训练预测 ########################
best_c = printing_Kfold_scores(X_train, y_train)
lr = LogisticRegression(C = best_c, penalty = 'l1')
lr.fit(X_train,y_train.values.ravel())
y_pred_undersample = lr.predict(X_test.values)
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test,y_pred_undersample)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
, classes=class_names
, title='Confusion matrix')
plt.show()
###########################################################################
########################### 修改阀值进行对比 ###############################
lr = LogisticRegression(C=0.01, penalty='l1')
lr.fit(X_under_train, y_under_train.values.ravel()) # 训练模型
'''
假定在一个k分类问题中,测试集中共有n个样本。则:
predict返回的是一个大小为n的一维数组,一维数组中的第i个值为模型预测第i个预测样本的标签;
predict_proba返回的是一个n行k列的数组,第i行第j列上的数值是模型预测第i个预测样本的标签为j的概率。
此时每一行的和应该等于1。
'''
y_pred_undersample_proba = lr.predict_proba(X_under_test.values)
print("y_pred_undersample_proba :", y_pred_undersample_proba)
threshholds = [0.1, .2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]
plt.figure(figsize = (10, 10))
j=1
for i in threshholds:
y_test_predictions_high_recall = y_pred_undersample_proba[:, 1] > i
plt.subplot(3,3,j)
j += 1
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_under_test, y_test_predictions_high_recall)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ",
cnf_matrix[1, 1] / (cnf_matrix[1, 0] + cnf_matrix[1,1]))
# Plot non-normalized confusion matrix
class_names = [0, 1]
plot_confusion_matrix(cnf_matrix,
classes = class_name,
title="Threshold >= %s" % i)
###########################################################################过采样的代码:
############################## 过采样 方法 ################################
credit_cards=pd.read_csv('creditcard.csv')
columns=credit_cards.columns
# The labels are in the last column ('Class'). Simply remove it to obtain features columns
features_columns=columns.delete(len(columns)-1)
features=credit_cards[features_columns]
labels=credit_cards['Class']
features_train, features_test, \
labels_train, labels_test = train_test_split(features,
labels,
test_size=0.2,
random_state=0)
oversampler=SMOTE(random_state=0)
os_features,os_labels=oversampler.fit_sample(features_train,labels_train)
os_features = pd.DataFrame(os_features)
os_labels = pd.DataFrame(os_labels)
best_c = printing_Kfold_scores(os_features,os_labels)
lr = LogisticRegression(C = best_c, penalty = 'l1')
lr.fit(os_features,os_labels.values.ravel())
y_pred = lr.predict(features_test.values)
# Compute confusion matrix
cnf_matrix = confusion_matrix(labels_test,y_pred)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
, classes=class_names
, title='Confusion matrix')
plt.show()
###########################################################################因为这是博主我刚学的机器学习,所以关于第5-7步也没有自己弄过,就不多说了,上面完整的步骤还是参考别人的。
最后:
原码:都在logistics regression的文件夹里。https://github.com/davidHdw/machine-learning/tree/master/Logistitc%20Regression
其中:Credit_card_fraud_detection是博主,tangyudi是唐宇迪老师的原版。
数据:链接:https://pan.baidu.com/s/1fzy0Gxp8a5f6m2H6LRQ-3w
提取码:rsit