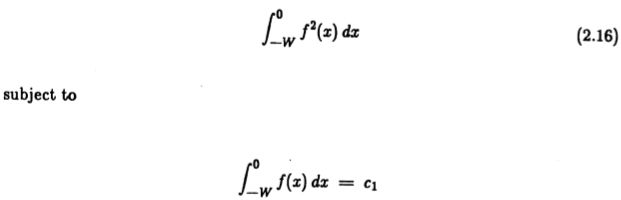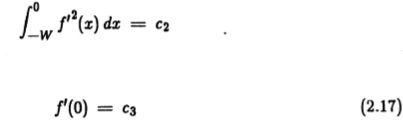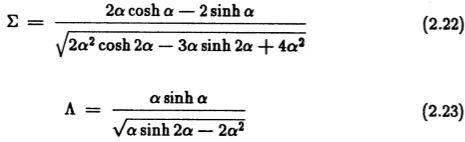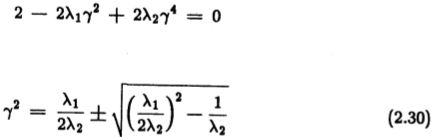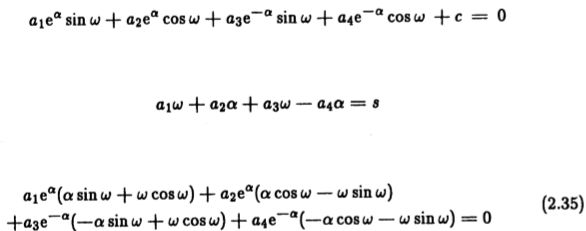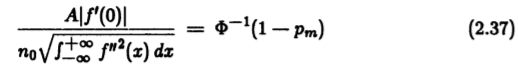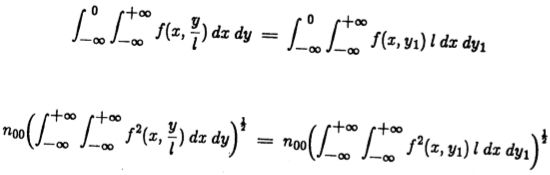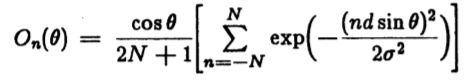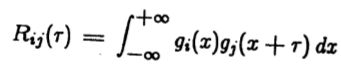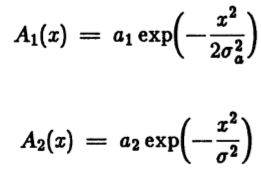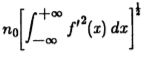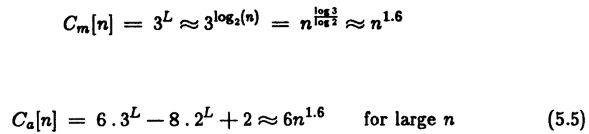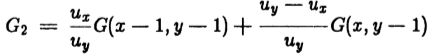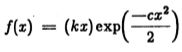此主要讨论图像处理与分析。虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来，但鉴于它们与计算机视觉的紧密联系，以 及它们的出处，没有把它们纳入到图像处理与分析中来。同样，这里面也有一些 也可以划归到计算机视觉中去。这都不重要，只要知道有这么个方法，能为自己 所用，或者从中得到灵感，这就够了。
8. Edge Detection
边缘检测也是图像处理中的一个基本任务。传统的边缘检测方法有基于梯度 算子，尤其是 Sobel 算子，以及经典的 Canny 边缘检测。到现在，Canny 边缘检 测及其思想仍在广泛使用。关于 Canny 算法的具体细节可以在 Sonka 的书以及 canny 自己的论文中找到，网上也可以搜到。最快最直接的方法就是看 OpenCV 的源代码，非常好懂。在边缘检测方面，Berkeley 的大牛 J Malik 和他的学生 在 2004 年的 PAMI 提出的方法效果非常好，当然也比较复杂。在复杂度要求不高 的情况下，还是值得一试的。MIT的Bill Freeman早期的代表作Steerable Filter 在边缘检测方面效果也非常好，并且便于实现。这里给出了几篇比较好的文献， 包括一篇最新的综述。边缘检测是图像处理和计算机视觉中任何方向都无法逃避 的一个问题，这方面研究多深都不为过。
[1980] theory of edge detection
[1983 Canny Thesis] Finding Edges and Lines in Images by Canny
[1986 PAMI] A Computational Approach to Edge Detection
[1990 PAMI] Scale-space and edge detection using anisotropic diffusion
[1991 PAMI] The design and use of steerable filters
[1995 PR] Multiresolution edge detection techniques
[1996 TIP] Optimal edge detection in two-dimensional images
[1998 PAMI] Local Scale Control for Edge Detection and Blur Estimation
[2003 PAMI] Statistical edge detection_ learning and evaluating edge cues
[2004 IEEE] Edge Detection Revisited
[2004 PAMI] Design of steerable filters for feature detection using canny-like criteria
[2004 PAMI] Learning to Detect Natural Image Boundaries Using Local Brightness, Color, and Texture Cues
[2011 IVC] Edge and line oriented contour detection State of the art
翻译
用Canny查找图像中的边和线
作者：John Francis Canny
摘要 -在视觉上检测图像强度变化的问题是规范的。边缘检测算子通常设计为在某些（通常很小）的支持上最优估计一阶或二阶导数。还提出了其他标准，例如输出信噪比或带宽。本论文试图制定一组边缘检测标准，以尽可能直接地捕获边缘算子的所需属性。使用变分技术在所有线性移位不变算子的空间上找到一个解。第一个标准是检测器具有较低的错误概率，即无法标记边缘或错误地标记非边缘。第二个是标记的点应尽可能靠近真实边缘的中心。第三个标准是，对单个边缘的一个以上响应的可能性应该很小。该技术用于为阶梯边缘和扩展的脉冲轮廓（二维的波峰或波谷）找到最佳算子。然后讨论一维运算符到二维的扩展。结果是一组宽度，长度和方向不同的运算符。讨论了将这些输出组合为单个描述的问题，并给出了一组用于集成的启发式方法。
致谢
首先，必须感谢我的主管米特·布雷迪（Mite Brady），他对这项工作的热情几乎是无限的，并且弥补了我不愿查阅文献的不足。 Mike还作为系统的主要用户提供了宝贵的反馈。
目录
1.简介
2.台阶边缘的一维公式
2.1不确定性原则
2.2步骤的最佳算子
2.3消除多重反应
2.4通过随机优化找到算子
3.二维及以上
3.1需要多种宽度
3.2对定向运营商的需求
3.3噪声估计
3.4滞后阈值
3.5对平滑渐变的敏感度
4 查找线条和其他特征
4.1标准的一般形式
4.2二维
5.实施细节
5.1离散化的影响
5.2高斯卷积
5.2.1 离散二维卷积
5.2.2 使用一维分解进行卷积
5.2.3 递归过滤
5.2.4 多项式逼近
5.2.5 快速卷积
5.2.6 子摘要
5.3非最大抑制
5.4 映射功能
6 试验
6.1噪声中的阶跃边缘
6.2 操作员集成
6.2.1 不同掩模宽度的集成
6.2.2 方向罩的集成
6.3寻线器
6.4 心理物理学
7 相关工作
7.1 表面拟合
7.2导数估计
7.3频域方法
8.进一步工作的结论和建议
附录I.微分中使用的定积分
参考文献
1.简介
边缘检测是许多视觉模块中的第一阶段，任何边缘检测器都应在适当的环境下制定。然而，许多模块的要求是相似的，似乎应该可以设计一个在几种情况下表现良好的边缘检测器。设计这种探测器的关键的第一步应该是捕获这些要求的一组性能标准的规范。这些标准的规范以及从中得出的最佳算子构成了本报告的主题。
边缘检测器的操作最好由图（1.1）中的示例说明，该示例由本报告中描述的检测器产生，该检测器接受离散的数字化图像并生成“边缘图”作为其输出，该边缘图包括关于边缘的位置和强度，其方向以及发生变化的“比例”的明确信息。尽管未明确显示，但也可以根据数量计算边缘的位置或强度的不确定性图（1.1）中的示例仅包含位置信息。
图1.1边缘检测器提供的位置信息应用于某些机械零件的图像
数字化图像包含大量冗余。信息理论上有冗余（可以将采样数据压缩为更少的位数，而不会显着更改重构的图像）。即使经过有效编码，剩下的大部分内容也对以后的视觉模块无用。这些模块通常需要结构信息，即表面取向的详细信息以及可见表面所包含的材料。在表面光滑且反射率均匀的情况下，可以应用阴影形状（Horn 1975）来获得表面方向。在许多其他模块中，例如运动产生的形状（Ullman 1979和Hildreth 1983），运动产生的轮廓（Stevens 1980），运动产生的形状（Witkin 1980）和立体声（Marr和Poggio 1979，Grimson 1981），下面的表面的结构特性是从边缘轮廓推断。特别地，强度的阶跃变化很重要，因为它们通常对应于锐利的方向或材料的变化或物体边界的变化。边缘检测是一种生成紧凑描述的方法，该描述将图像中的大多数结构信息保留下来。
某些先前的公式已选择一阶或二阶导数作为表征阶跃边缘的适当量，并在某种支持下形成了对该导数的最佳估计。一阶导数算子的例子是Roberts（1965）和Macleod（1970）的算子，而Modestino和Fries（1977）在较大的支持下形成了二维拉普拉斯算子的最佳估计。 Marr和Hildreth（1980）提出了广义高斯的拉普拉斯算子，因为它优化了本地化和带宽的权衡。但是，拉普拉斯算子存在问题，并且导数估计的整个概念似乎基础很差。这些批评将在第7章中具体说明。
存在第二主要类别的公式，其中图像表面由一组基函数近似，并且边缘参数从建模的图像表面估计。这种技术的例子包括Prewitt（1970），Hueckel（1971）和Haralick（1982 ）的著作。这些方法允许对边缘属性（例如位置和方向）进行更直接的估计，但是由于基本功能通常不完整，因此这些属性仅适用于实际图像表面在基本功能所覆盖的子空间上的投影。但是，基本功能是操作员性能的主要因素，尤其是其对边缘进行定位的能力。
在本报告中，我们从传统的高斯白噪声阶跃边缘模型开始，并尝试精确地制定有效边缘检测的标准。 我们假设检测是通过将噪声边缘与空间函数 f（x）卷积（我们正在尝试找到）并在此卷积输出的最大值处标记边缘来执行的。 然后，我们在此运算符的输出上指定三个性能标准。
（i）良好的检测。不能标记真实边缘点的可能性较低，并且错误标记非边缘点的可能性较低，因为这两个概率都是输出信号信噪比的单调递减函数，因此该标准对应 最大化信噪比。
（ii）良好的定位：操作员标记为边缘的点应尽可能靠近真实边缘的中心。
（ii）仅对单个边缘的响应：由于两个附近的操作员对同一边缘做出响应，因此在（i）中隐式捕获了该响应，因此必须将其中一个视为假边缘。但是，第一个准则的数学形式并未满足多重响应要求，因此必须明确。
分析阶跃边缘的第一个结果是（i）和（ii）相互冲突，并且它们之间存在折衷或不确定性原则。广泛的运营商具有良好的信噪比，但定位较差，反之亦然。对于定位标准的数学形式的简单选择给出了定位项和恒定的信噪比的乘积。函数 f（x）的空间缩放将改变信噪比和定位的各个值，但不会改变其乘积。给定检测函数的解析形式，理论上我们可以通过缩放而不是同时从缩放中获得任意良好的信噪比或本地化。从分析中我们可以得出结论，函数 f 有一个最佳形状，该形状可使乘积最大化，并且如果我们对其进行缩放以实现其中一个准则的某个值，则它将同时为另一个准则提供最大值。为了处理各种图像，边缘检测器需要使用几种不同宽度的运算符，并以连贯的方式将它们组合在一起。通过将边缘检测的标准形成为未知算子 f 的一组功能，我们可以使用变分技术来找到使标准最大化的函数。
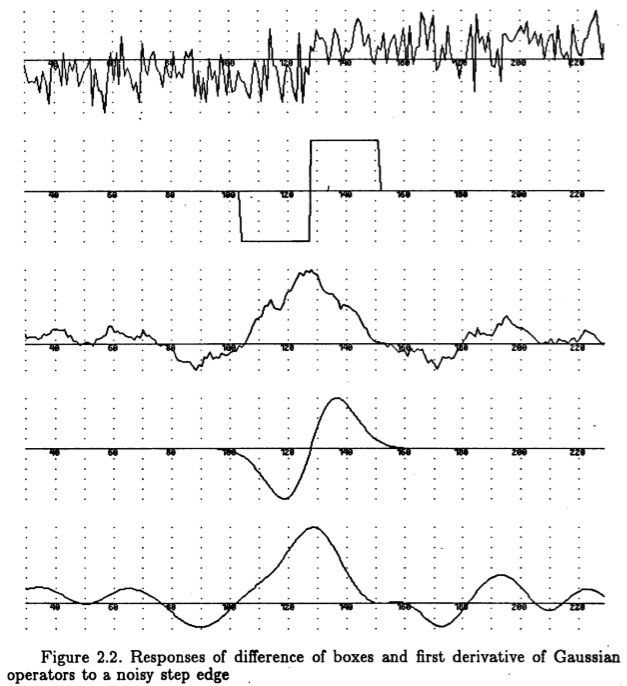
第二个结果是标准（i）和（ii）本身不足以产生有用的边缘检测器。 似乎我们可以通过使用盒子运算符的差异来获得最大的信噪比和任意良好的定位。 Rosenfeld和Thurston （1971）提出了盒子的差异（见图2.2），Herskovits和Binford（1970）曾使用过盒子的差异，如果我们仔细观察这样一个算子对嘈杂的阶跃边缘的响应，我们会发现存在 输出最大值靠近边缘的中心，但是附近可能还有许多其他值。我们没有取得很好的定位，因为无法分辨出最大值中的哪一个与真实边缘最接近。 ）使操作员响应单个边缘给出多个最大值的可能性非常低，并且还导致定位和信噪比乘积的有限极限。
第三个结果是运算符的解析形式，它是四个复指数的和，可以用高斯的一阶导数近似。首先使用随机爬山技术找到了对此函数的数值有限维近似。这样做是因为，将确定性形式的多重响应标准写为数值优化方法比f函数更容易。具体而言，数值优化器提供候选输出以进行评估，而对其中一个输出的最大值进行计数是一件简单的事情。为了解析地表达此约束，我们需要找到对边的响应中的最大值的期望值，并将其表达为f上的函数，这要困难得多。以前曾提出过高斯的一阶导数（Macleod 1970）。还值得注意的是，在一个维度上，该一阶导数运算符的输出的最大值对应于一二阶导数运算符的输出的零交叉。
其他一些结果涉及将操作员扩展到两个（或多个）维度。可以粗略地概括它们，说检测器应该是定向的，如果图像允许，定向越多越好。非方向性（拉普拉斯）与方向性边缘算子的问题一直是争论的话题，例如将Marr（1976）与Marr and Hildreth（1980）进行比较。结果表明，与拉普拉斯算子相比，本地化更好，信噪比更好，如果使用有效的算法，则计算方向分量所需的计算量很小，最后，将多个方向的算子组合在一起的问题很困难，但并非难事。例如，要合并不同大小的运算符的输出要困难得多，因为它们的支持明显不同。对于给定的运算符宽度，信噪比和本地化都随着运算符的长度（平行于边缘）而提高当然，只要边缘不偏离直线就可以增加。当图像确实包含较长的近似笔直的轮廓时，高度方向性的运算符是最佳选择。这意味着将需要几个操作员来覆盖所有可能的边缘方向，并且还需要较少方向性的操作员来处理局部不直的边缘。
以与操作员推导类似的方式来解决组合不同的操作员宽度和方向的问题。我们从同一套标准开始，然后尝试选择能够提供良好信噪比和最佳定位的运营商。我们设置了最小可接受的错误率，然后选择信号噪声比错误率确定的阈值更大的最小运算符。这样，全局错误率是固定的，而特定边缘的定位将取决于局部图像信噪比。从一组方向算子中选择最佳算子的问题比较简单，因为只有一个或两个会响应特定方向的边缘。在方向性较长的操作员和方向性较小的操作员之间进行选择的问题在理论上很简单，但在实践中却很困难。高度方向性的运算符显然是更可取的，但不能用于局部弯曲的边缘。有必要将拟合优度与每个操作员相关联，以表明图像与线性扩展步骤模型的拟合程度。当边缘足够好时，将使用定向运算符输出，并且将抑制定向性较差的邻居的输出。
虽然台阶边缘的检测是该报告的主要目标，但第4章给出了最佳性标准的一般形式。使用这种通用形式，可以为任意特征设计最佳算子。在给定要检测的输入波形的情况下，使用数值优化来查找操作员的脉冲响应。通过推算山脊，屋顶和台阶边缘的运算符可以说明该技术。其中的脊和阶跃检测器已在真实图像上进行了测试。讨论了将一维脊线算子扩展到二维的特殊问题，以及对阶跃和脊线检测器输出进行积分的问题。
在分析之后，我们概述了一些简单的实验，这些实验似乎表明人类视觉系统正在执行类似的选择（在某些计算级别上），或者至少表明其执行的计算具有相似的目标集。图像的模糊会导致图像细节模糊，这与操作员的几种尺寸一致。更有趣的是，噪声的添加可能使人们能够大规模感知变化，即使这些变化存在于原始图像中，但由于存在锐利的边缘而很难感知。噪声的加入也降低了我们感知近似笔直边缘的微小波动的能力，但笔直边缘的印象却没有。
作为读者的指南，第2章和第3章构成了阶跃边缘分析的核心，它们还包含了大多数信号理论，普通读者可能希望略过它们。第3章的第一部分应该阅读 但是，因为它包括将理论运算符转换为实用算法。 第4章比较容易理解，并且包含有关最优性标准的更一般形式。 它提供了解决屋顶和山脊边缘变化问题的示例。 第5章的标题为“实现细节”，可能会想避免将其级别太低，但是它包含几种用于高斯卷积的有效算法，并且可能在本工作范围之外具有应用。最后，第6章 和7通过显示操作员在真实图像上的性能并将其与其他一些边缘检测器在实验和理论上进行比较，从而对分析进行了加权。
2. 台阶边缘的一维公式
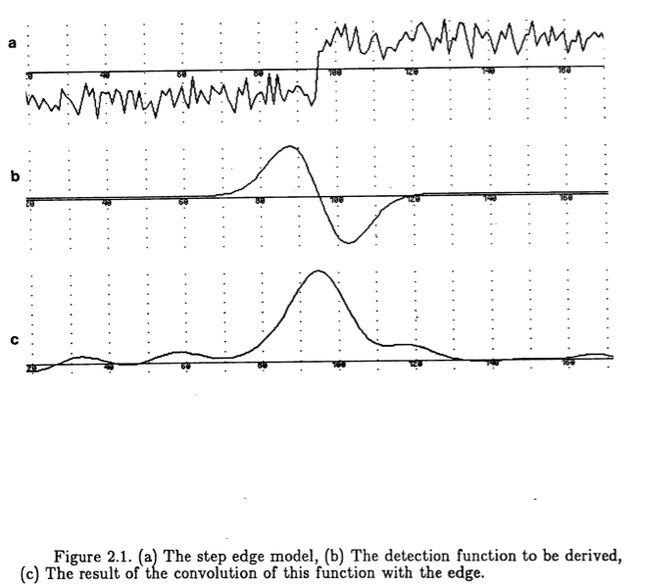
基本设计问题如图（2.1）所示。我们试图检测浸入高斯噪声的阶梯边缘，如图（2.1a）所示。我们用一些空间函数（2.1b）进行卷积，并在此卷积（2.1c）的结果中将最大值标记为边缘。目的是找到给出“最佳”输出的空间函数（称它为 f），其中最佳是由台阶边缘检测的一组精确标准定义的。
图2.1：（a）阶梯边缘模型，（b）要导出的检测函数，（c）该函数与边缘的卷积结果。
关于符号的一些初步说明；当我们说边缘检测“算子”时，是指从一维或二维强度函数（图像或穿过它的线性切片）到相同维度的强度函数的映射。如果算子是线性的且位移不变，则可以用强度函数与算子的“脉冲响应”（一维）或“点扩展函数”（二维）的卷积来表示，这就是结果移不变性显然是边缘算子的一个理想特性。首先，我们将仅考虑线性移位不变算子，随后我们将决策程序应用于其输出，这将导致移位不变非线性算子。描述从图像到边缘轮廓的最终表示的映射的操作员称为“边缘检测器”。
设计有效边缘运算器的关键是对其性能的准确评估。如果我们可以用封闭的数学形式写下评估函数，则可以应用标准工具（例如，变化的演算）来找到将其最大化的运算符。与许多优化问题一样，获得有用答案的关键是提出正确的问题。边缘检测问题也不例外，这在推导过程中将变得显而易见。必须先对评估功能进行几项操作，然后才能发现该功能已关闭所有漏洞”，并排除了出于“显而易见”原因而不切实际的运算符。这并不是说问题已成为提出适合所建议解决方案的问题之一，而是问题始终是相同的，只是很难用封闭形式表示，该形式足够简单以产生变分问题可以解决的。相比之下，使用蒙特卡洛优化来获得类似的解决方案相对容易，因为可以直接在候选算子的输出上进行评估。那么，真正的问题是将直观的性能目标转换为直接取决于操作员形式的功能。本节介绍翻译过程中的主要阶段。
2.1 不确定性原则
我们首先考虑一维边缘检测问题，目标是检测并标记包含加性白噪声的信号中的阶跃变化。我们假设信号在不连续的两面都是平坦的，并且没有其他边缘足够靠近以影响运算符的输出（见图2.1）。我们需要以某种方式将准确检测和定位的两个目标结合到一个评估功能中。检测标准很容易用操作员输出中的信噪比来表示，即响应于阶跃输入的输出与仅响应噪声的输出之比。定位标准比较困难，但是合理的选择是真实边缘与检测器标记的边缘之间的距离的倒数。对于距离测量，我们将在操作员输出最大值的位置使用标准偏差。通过使用局部最大值，我们正在做出从线性算子输出到检测器输出的映射中似乎是任意的选择。但是，映射必须包含一些局部谓词，并且由于我们正在设计一个线性运算符，该线性运算符将强烈响应阶跃边，因此其响应最大值是一个合理的选择。
令步幅为A，使噪声为 n（x）。那么输入信号 I（x）可以表示为
其中
是定义为的单位步长函数
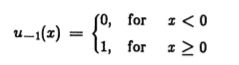
让我们要寻找的算子的脉冲响应由函数 f（x）表示。 然后，由卷积积分给出运算符对输入 I（x）的应用的输出 O（x0），
我们可以使用卷积的线性度将此积分分为仅由于阶跃和噪声引起的贡献。 仅由于该步的输出是（在该步的中心，即x0 = 0）
虽然仅对噪声分量的均方响应为
其中E [y]是y的期望值。 如果噪声为白噪声，则上述内容简化为
其中，对于所有x，
，
是输入噪声的方差。我们将输出信噪比定义为仅对阶跃响应的商和均方根 平方噪声响应。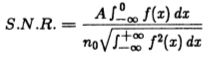
根据该表达式，我们可以定义操作员的信号至噪声性能的量度
，该量度与输入信号无关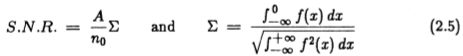
这就是我们双重标准的第一部分，找到使它最大化的脉冲响应f 对应于找到仅用于检测的最佳算子。
对于本地化标准，我们进行如下操作。回想一下，我们选择在运算符的输出中标记最大值处的边。对于理想的步骤，我们希望边缘的中心有一个最大值。由于信号I（x）包含噪声，因此我们希望此最大值从边缘的真实位置（在本例中为原点）处移开。为了获得随操作员的定位能力提高而提高的性能度量，我们使用实际最大值与真实边缘中心的距离的标准偏差的倒数。这不是一个任意选择，因为它提供了一个与规模无关的复合性能标准，正如我们将看到的。
运算符的输出O（x0）的最大值对应于该输出的空间导数的零交叉。 我们希望找到 x0 的位置
通过卷积的微分定理可以简化为
为了找到 x0，我们再次将输出
的导数分为阶跃和仅由于噪声（分别称为
）而组成。
导数滤波器仅对噪声的响应（在任何输出点）将是高斯随机变量，其均值为零且方差等于均方输出幅度
现在，我们添加了约束，即函数f应该是反对称的。 任意函数始终可以分为对称和反对称分量，但是应该清楚的是，对称分量对操作员的检测或定位能力没有任何影响，但会对影响两者的噪声分量有所贡献。 
关于原点的泰勒展开式给出
对于输出
的零交叉，我们要求
用（2.7）和（2.8）的两个输出代替，我们得到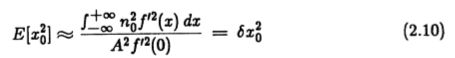
其中
是实际最大值与真实边距的标准偏差的近似值。局部化定义为的倒数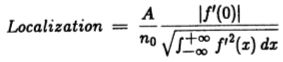
同样，我们定义一个绩效度量
，它仅是运营商的一个属性
获得了我们两个期望的标准后，我们现在遇到了以下问题：
以有意义的方式将它们结合起来。 事实证明，如果我们使用这两个标准的乘积，我们将获得一个与幅度和比例无关的度量。 该度量仅是脉冲响应f的形状的属性，并且对于通过空间缩放从f 获得的所有函数 
都是相同的。 实际上，组合的选择不会影响解决方案的形式，因为变分方程仅取决于准则中的各个术语。 这两个条件的乘积是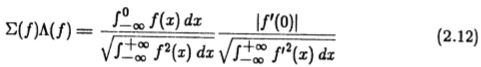
为了说明该准则在尺度变化下的不变性，我们考虑脉冲响应为的算子的性能，其中
。
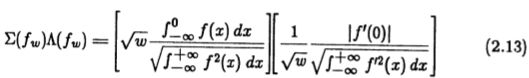
其中带括号的术语对应于检测和定位标准。从这种形式我们可以看到，运营商的信噪比随
变化，而定位随的倒数而变化。具有宽脉冲响应的操作员将具有良好的信噪比，但定位较差，反之亦然。但是，使用这种形式的复合标准，检测和定位项的乘积对于所有都是相同的。
该结果表明，有几类具有最佳性能的运算符，并且它们与空间比例相关。实际上，该结果与标准组合的选择无关。为了看到这一点，我们假设有一个函数f给出了特定
的最佳位置
。也就是说，我们找到f 使得
现在假设我们寻找第二个函数，该函数给出最佳的可能定位，同时将其信噪比固定为一个不同的值。
如果我们像以前那样定义，则
，如果设置为
然后，在（2.15）中对 的约束转化为对f的约束，该约束与（2.14）相同。 因此，为了解决（2.15），我们找到f 使得
具有与（2.14）相同的解决方案。因此，如果我们找到一个这样的函数f ，则可以通过缩放f获得任何固定信噪比的最大局部化。因此，我们对复合标准的选择不是任意的，而是强调了自然约束或“不确定性原理”，用于检测噪声中的阶跃边缘。我们可以通过缩放获得任意良好的定位或检测，但不能同时获得两者。
我们将（最终）发现上述分析是有效的，但所给出的标准仍未明确。尽管确实导致了合理的解决方案，但是性能仍然很差，因为到目前为止我们都忽略了检测过程的重要方面。即，检测器不应响应单个边缘而产生多个输出。在下一部分中，我们将找到上述优化问题的解决方案，并着重说明它们在多重边缘响应方面的弱点。
2.2 步骤的最佳算子
最优边缘检测算子现在已经由等式（2.12）隐含地定义。剩下的就是找到一个最大化此大型表达式的函数。我们必须先进行一些简化，然后才能使用变化演算找到解决方案。由于每个方程都取决于f（zx），因此我们无法直接找到使方程（2.12）中的积分商最大化的函数。相反，我们以类似于拉格朗日乘数法的方式将除一个积分外的所有积分都设置为未确定的常数。然后，我们根据未确定的常数找到相关积分的极值（因为它将对应于总表达式中的最大值）。然后选择常量的值，以便最大化表达式其余部分的值，该表达式现在仅是三个常量的函数。给定这些常数，我们可以完全唯一地指定函数 f（x），该函数给出准则的全局最大值。
第二个简化涉及积分的极限。分母（2.12）中的两个积分在正无穷大处有极限，而分子的积分在零无穷大而在负无穷大处有一个极限。由于函数f应该是反对称的，因此我们可以对所有积分使用后者的极限。分母积分在该子范围内的值将是它们在f 范围内应有的值的一半。而且，这使得能够将 f'（0）的值设置为边界条件，而不是表示为f” 的积分。负无穷大时所有积分的下限应设置为某个有限的负值，例如-W，因为我们将处理有限范围的算符。这些简化使我们能够利用等压约束条件（请参见Courant和Hilbert 1953）。这使我们能够将一组约束积分组合在一起，这些约束积分与被积分的极限具有相同的极限，成为一个变分方程。
因此，找到方程（2.12）的最大值的问题减少为在S.N.R.的分母中找到积分的最小值的问题。 项，但要遵守其他积分保持不变的约束。 根据互惠原则，我们可以选择对任何一个积分求极值，同时保持其他积分不变，但解应相同。 我们从允许函数的空间中寻找一些函数f，该函数应使积分最小化
在这种情况下，允许函数的空间将是满足某些边界条件的所有连续函数的空间，即 f（0）= 0 和 f（-W）= 0。这些边界条件对于确保在有限极限上评估的积分准确地表示无限卷积积分是必要的。也就是说，如果f的n阶导数出现在某个整数中，则该函数的（n-1）st导数必须在（一oo，+ oo）范围内是连续的。这意味着 f 及其一阶（n-1）导数的值在积分极限时必须为零，因为它们在此范围之外必须为零。
要最小化的函数的形式为
，我们有一系列约束可以以
的形式编写。由于约束是等距的，即它们与最小化的积分具有相同的积分极限，因此我们可以形成复合函数
作为表达式中出现的函数的线性组合。 （Courant and Hilbert 1953）。为这个不受约束的问题找到解决方案等同于为受约束的问题找到解决方案。复合功能是
代，
从该方程的形式可以看出，对哪个积分进行了极值的选择和哪些约束是任意的，其解将是相同的。 这是变分问题中所谓的互惠的一个例子。 从分母中选择积分非常方便，因为欧拉方程的标准形式适用于最小化问题。 对应于该函数的欧拉方程为
其中
表示
相对于f 的偏导数。
这个微分方程的一般解是
其中
且常数 a1 和 a2 由边界条件f（0）= 0 和f（-W）= 0 确定。 添加这些约束后，函数f 可以用以下形式编写：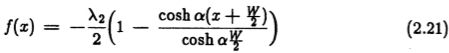
从中我们可以得到信噪比和定位的表达式，该表达式是参数入1和入2的函数。 为了简化表达式，我们将假设宽度W为2，并利用公式（2.13）的缩放比例属性。 这给
这两个表达式仅是
的函数，我们可以研究f的行为，因为趋于其极限值0和+ oo。当a趋于零时，我们发现函数f趋于方程为
信噪比和定位的相应值为
当一个值接近无穷大时，我们发现该函数在（-2,0）范围内接近一个常数（回想W = 2），并且信噪比趋于1。 趋于零，相对于相应值的增加很小。 但是，本地化术语会无限增加。 从这个结果看来，盒函数的差异（派生函数在范围[-2,2]上的反对称扩展）给出了最佳的信噪比，并且具有良好的局部性。 实际上，该功能是阶梯边缘的最佳维纳滤波器。
该运算符由于其简单性和易于计算而被广泛使用，如Rosenfeld和Thurston（1971）的工作，并与Herskovits和Binford（1970）的横向抑制相结合。然而，它具有非常高的带宽，并且倾向于对嘈杂的台阶边缘表现出许多最大值，这在成像系统添加噪声或图像本身包含纹理化区域时是一个严重的问题。根据我们的第一个标准，这些额外的边缘应被认为是错误的。但是，该标准的解析形式是从单个点（边缘的中心）处的响应派生的，并且没有考虑多个附近点处响应的交互作用。我们需要通过在解决方案中添加进一步的约束来使其明确。
2.3 消除多重反应
如果我们检查盒子边缘检测器差异的输出，我们发现对噪声阶跃的响应是一个近似三角形的峰值，在边缘附近有许多尖锐的最大值（见图2.2）。这些最大值非常接近，以致于不可能选择一个作为对步的响应，而将其他识别为噪声。我们需要在标准中添加以下要求：函数f对a的响应不会“太多”台阶附近的单个台阶边缘。我们需要限制响应中的峰值数量，以便声明多个边缘的可能性很小。理想情况下，我们希望使噪声响应中的峰值之间的距离近似于操作员响应的宽度一步。该宽度将与操作员宽度W大致相同。
为了将其表示为对f的功能约束，我们需要获得相邻噪声峰之间距离的表达式。 我们首先注意到输出中相邻最大值之间的平均距离是算子输出导数中相邻零交叉之间距离的两倍。 然后，我们利用Rice（1944,1945）的结果得出，函数g 对高斯噪声的响应的零交叉点之间的平均距离为
其中
是g的自相关函数。在我们的案例中，我们正在寻找函数 f' 的平均零交叉间距。 现在，因为
f' 的零交叉之间的平均距离为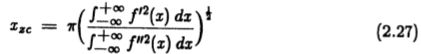
f的噪声响应中相邻最大值之间的距离（表示为
）将为
的两倍。 我们将此距离设置为运算符宽度的几分之一k。
图2.2： 盒子和高斯算子的一阶导数之差对噪声阶跃边缘的响应。
由于
的积分已从本地化准则开始出现在
中，因此这一新约束仅向复合函数添加了一项。 虽然在原始函数中此积分出现在要最大化的量的分母中（即定位准则），但现在它出现在最大值之间的平均距离的分子中，这是对解的约束。 现在不再清楚其拉格朗日乘数应该是什么符号。 正如我们将看到的，这为f提供了几种可能的解决方案。 新功能由
对应于二阶泛函的欧拉方程为
当上述代入欧拉方程后，我们得到
此微分方程的解是一个常数和一组
的四个指数的总和，其中
是从相应齐次微分方程的解中得出的。 现在
根据
的值，该方程可能具有纯虚数，纯实数根。根据复合函数
，我们可以推断
为正（因为
将被最小化），但不清楚
符号或 的大小应该是。 欧拉方程为存在最小值提供了必要条件，但它不是充分条件。 通过制定这样的条件，我们可以解决入值的歧义。 为此，我们必须考虑功能的第二种变化。让
然后根据泰勒定理，
其中p 是介于0和
之间的某个数字，而g 是从允许函数的空间中选择的，其中
请注意，J1 仅不过是g的f 的欧拉方程的积分（乘以部分积分变换），并且如果 f 满足欧拉方程，则J1 将为零。 现在我们可以将第二个变化
定义为
最小值的必要条件是>= 0。 我们可以用（2.29）代替的二阶偏导数，得到
我们通过零件集成将其转换为
可以写成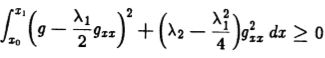
如果对所有x积分的表达式均为正，则保证积分为正，因此，如果
那么对于所有x 和任意g ，积分将为正，并且极值必定为最小值。 如果我们回到（2.28），我们发现这个条件恰好是的复数根，因此我们既保证了最小值的存在，又以解的形式解决了可能的歧义。 现在，我们可以继续推导，并假设形式为
的四个复数根，其中
，w 为实数，使得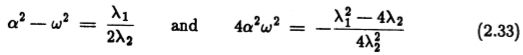
现在可以编写一般解决方案
此功能受边界条件的限制
其中s 是一个未知常数，等于函数f在原点的斜率。 这四个边界条件使我们能够根据未知常数，w，c 和s 求解 a1 至a4 的量。 边界条件可能会被重写
这些方程在四个未知数a1，a2，a3，a4 中是线性的，求解后得出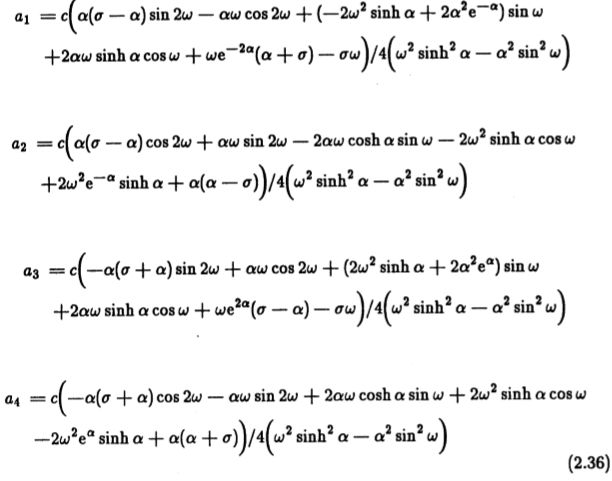
其中
是原点处的斜率s 除以常数c 。 通过检查这些表达式，我们可以看到，可以通过将a3 替换为一个 -来从a1中获得
，类似地，可以从a2中获得a4。
现在根据常数，w，和c对函数f 进行了半参数化。我们仍然需要找到这些参数的值，以使构成我们的复合准则的积分商最大化。为此，我们首先用常数表示每个积分，由于这些积分非常长且无趣，因此不给出它们在这里，但是为了完整起见，它们被包含在附录I 中。我们已经将函数的无穷维空间上的优化问题简化为三个变量数，，和（如预期的那样，是组合准则）的非线性优化。不依赖于c）。不幸的是，仍然必须满足多重响应约束的结果准则可能太复杂而无法解析解决，必须使用数值方法来提供最终解决方案。
实际上，对于给定的W，确实有一个最佳函数f ，因为它的形状将取决于多重响应约束，即它将取决于我们强制相邻响应的距离。图（2.3）显示了该距离的特定选择所产生的运算符。回想一下，对于任意w，没有单个最佳函数，而是通过缩放原型获得的一系列函数，用w函数随着图像中信噪比的降低。我们希望将响应进一步拉开，并且不清楚单个操作员的信噪比值是多少。但是，这种设计是基于使用多个宽度的运算符，并基于一个决策程序，该程序选择输出信噪比高于给定阈值的最小运算符。这要求所有操作员将大部分时间的操作剂量花费在其输出E阈值上。因此，我们应该尝试选择一个在这些条件下能给出可接受的多重响应行为的间距。
可以如下形成对真实最大值附近的虚假最大值的概率的粗略估计。 回想一下，运算符输出中的最大值对应于该输出的导数中的腐蚀。 如果我们看一看对理想步骤的响应的一阶导数，我们会发现它在步骤中心附近近似线性。 如果此响应的斜率大于仅对噪声的响应的斜率，则将只有一个航空降噪效果。 后一个斜率仅是对噪声响应的二阶导数，并且是具有标准偏差的高斯随机变量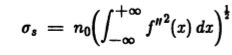
而边缘中心的零交叉的斜率是
。 前斜率超过后者的概率
由正态分布函数
给出
我们可以为此概率选择一个值作为可接受的错误率，这将确定f（0）与
的比率。
我们可以看到此约束对图像信噪比的显式依赖。 我们可以通过将多重响应 的概率与错误定义边缘pf 的概率相关联来消除这种依赖性，
我们终于有了
其中k是由两个概率的值确定的常数。 如果我们选择将设置为pf，则k的值为1。 不幸的是，可以使用约束数值优化获得的k的最大值约为58。这对应于最大间距为1.2（以W为单位）。 这是我们将使用的线性运算符的最终形式。 它在图（2.3）的系列图的最后一部分中进行了说明。 它的性能由
的乘积给出，并且具有
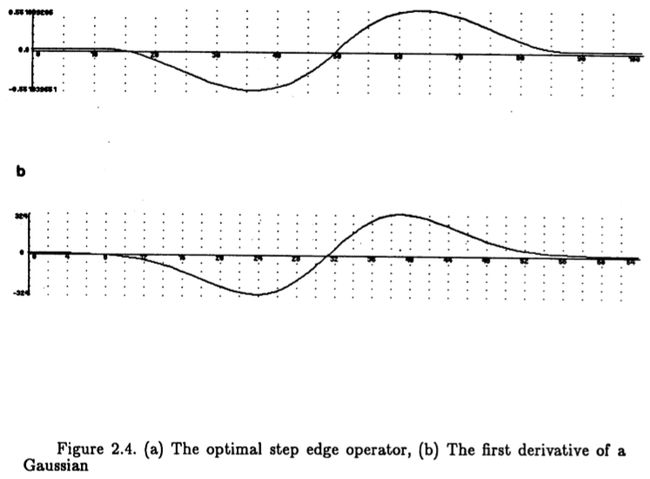
对图（2.3）中该算子的形状的检验表明，可能可以使用高斯G'的一阶导数对其进行近似，其中
这样做的原因是，如果可以将滤波器表示为高斯的某种导数，则有非常有效的方法来计算滤波器的二维扩展。 这将在第5章中详细讨论。现在，我们将高斯滤波器的一阶导数与最优算子的性能进行比较。 滤波器的脉冲响应现在为
绩效标准中的条款具有价值
图2.3：各种k值的最佳阶梯边缘算子，从上到下分别为k = 0.075、0.15、0.25、0.5、0.65、0.7
该运营商的整体绩效指数是
尽管此文件的k值为（2.38），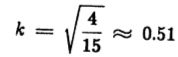
该运算符的性能比最佳运算符的性能差约20％，而其其多重反应量度k 的性能差约10％。 通过在真实图像上观察两个算子的性能来检测这种幅度的差异可能是困难的，并且因为可以在两个维度上用更少的精力来计算高斯算子的第一阶导数（但请参见第5.2 节）， 它仅用于实验中。 可以将两个算子的脉冲响应进行比较（图2.4）。
2.4 通过随机优化找到算子
图2.4 （a）最佳阶梯边缘算子，（b）高斯的一阶导数
上一节包含了用于阶梯边缘的最佳边缘检测器的“闭合形式”的推导，即使在为操作员推导此闭合形式时，也必须进行数值优化以获取以其解析形式出现的系数。看到这种方法需要求解非常复杂的非线性方程组的系统，如果将该技术应用于其他探针，则极有可能为运营商找不到封闭的解决方案。但是，这并不意味着不能使用这些技术得出有用的运算符。有两种替代方法，这两种方法都用于推导阶跃边缘算子，并且当表达式变得太复杂而无法求解时，可以应用这两种方法。
（i）第一部分在上一节中使用过，一旦解决方案简化为参数形式，就涉及使用数值方法来确定一些有限数量的参数值。实际上，如果满足对（无限滤波器的）带宽的适当约束，则即使是无限维的对象，例如滤波器的脉冲响应，也可以由有限维的离散滤波器来近似。所需要的只是确定性标准，该确定性标准可以应用于操作员的参数形式，并且可以根据该标准测量操作员的“好”。
（ii）当甚至不可能为最优性标准写下封闭形式时，第二种方法是必要的。 当图像模型包含一些随机成分（例如高斯噪声）时，就会出现此问题，然后有必要形成一些标准，以反映一些有意义的统计量，这些统计量是关于运营商在影像整体上的行为的。 高斯独立的随机过程特别容易分析，但是即使有了高斯统计量，阶跃边的封闭形式标准也导致了非常复杂的解。 但是，在本文的进一步工作部分，我们将提出一种将涉及某些平稳过程的问题转换为仅涉及高斯独立过程的等效探针的方法。
实际上，在撰写本报告之前，已经成功使用了第二种方法，然后才获得使用第一种方法的封闭式解决方案。 这几乎可以肯定是规则，而不是例外。 尽管充其量来说，随机方法可以得出近似解，并且如果参数空间的条件差，则可能不可行，但仍认为这是一种有用的技术，可以指导寻找解析解。
与分析方法一样，随机方法从图像模型开始。 再次，我们考虑了具有叠加高斯白噪声的阶梯边缘。 我们寻求一个滤波器f，该滤波器可以最大化某些准则，但是在这种情况下，我们无法通过其（无限）脉冲响应来表征滤波器。 相反，我们考虑使用离散滤波器，即通过在位置
等处采样的脉冲响应来表示滤波器。 假设相应的连续脉冲响应滤波器的带宽小于奈奎斯特频率
，则连续滤波器可以用其离散逼近来完全描述。 事实证明，对于带宽较小的阶跃边缘算子，仅需要大约12个样本。 在完成优化之前这是未知的，并且将32个样本用于离散滤波器。
优化算法本质上是对可能的过滤器空间进行爬山搜索。 通过连续迭代以下步骤来进行
（i）通过将高斯随机数添加到阶跃边缘的采样值来创建（离散的）噪声边缘。
（ii）将滤波器与此边缘卷积，并评估响应。
（iii）少量干扰滤波器系数（采样值）。
（iv）使这个新的滤波器与边缘卷积，并评估新的响应。
（v）根据（iii）中的扰动效果更换过滤器。
请注意，即使在解析解空间为凸形的情况下，也不能保证此过程会导致解。 它与确定性爬山程序不同，因为“小山”（参数空间中恒定评估的轮廓）不是固定的，而是随迭代而变化的。 在任何特定的评估中，由于建模图像中存在噪声而导致存在随机成分。 我们只能说，许多此类评估的平均值的极限将是从确定性标准中获得的轮廓。 实际上，由于滤波器系数的扰动，由图像变化引起的变化的幅度大大超过了变化的幅度。 因此，将干扰的和原始的滤镜应用于同一图像非常重要。
为了了解该方法何时收敛，我们假设存在确定性评估函数。 F在参数空间上，这样我们就可以局部估计参数
的n元组的评估为
其中r是来自某个未知分布的随机变量，该随机变量对图像噪声的影响进行建模。 如果我们现在将滤波器系数微调到
，我们将获得新的评估
假设 r 的值在的某个小邻域内是恒定的（图像未改变）。如果我们从 E2减去E1并除以 ||
现在
其中
是 方向上的单位向量。 通过使用n 个法向扰动i 和n个对应的单位向量i 并形成和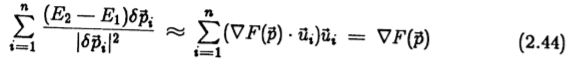
我们在参数空间中的点
处形成了评估函数梯度的估计。 估计
的另一种方法是使用随机分散的扰动。 通过随机分布，我们的意思是 的每个分量都是一个独立的随机变量，均值为零，方差
。 然后，由于评估变化而扰动的期望值是
因此，我们还可以通过对滤波器系数进行随机扰动并通过评估的变化对这些扰动进行加权来估算的梯度。 与对正交扰动的特定选择相比，此方法提供了一个在单个偏旁器空间点周围的邻域的更均匀的覆盖范围。 该实现使用随机扰动和短期平均滤波器来获得对多个迭代的F 梯度的估计。 所使用的滤波器具有单极点（即其对脉冲的响应是指数衰减序列），可以用差分方程式来描述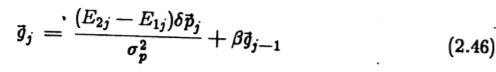
其中
是f 在第j 次迭代中f的梯度的估计，下标量
是在第j 次迭代中这些量的值。
是介于0和1之间的时间常数，它确定系统的“惯性”。
该算法通过在每次迭代中获取梯度的估算值并将其倍数与的当前值相加来执行简单的爬坡。但是，我们已经（有必要）在的估算器中添加了一个时间常数，以便我们可以获得不断更新的估算值，同时使用现有估算值进行爬升。现在，我们有了一个系统，它既具有先前迭代中的平均值的“惯性”，又具有由于该平均值随时间衰减 （假设小于1）而引起的“粘度”。因此，它有可能超过最小值，甚至在达到最小值之前振荡几次。有必要凭经验设置时间常数，以便获得准确的坡度估算值而又不过分。该系统的行为大致类似于在重力影响下沿轮廓表面滚动的球，具有完美的粘性阻力。
求助于随机方法进行优化的主要原因是评估标准是特定响应的函数，而不是对大量输入上的滤波器行为的估计。但是抽象标准应该相同。启发式准则应评估错误率和操作员的定位能力。实际使用的标准是
其中
是在固定边缘附近出现的局部最大值的数量，而
是最强最大值与真实边缘中心的距离。 注意，表达式中的两个术语是“惩罚”措施，因此是两个否定。
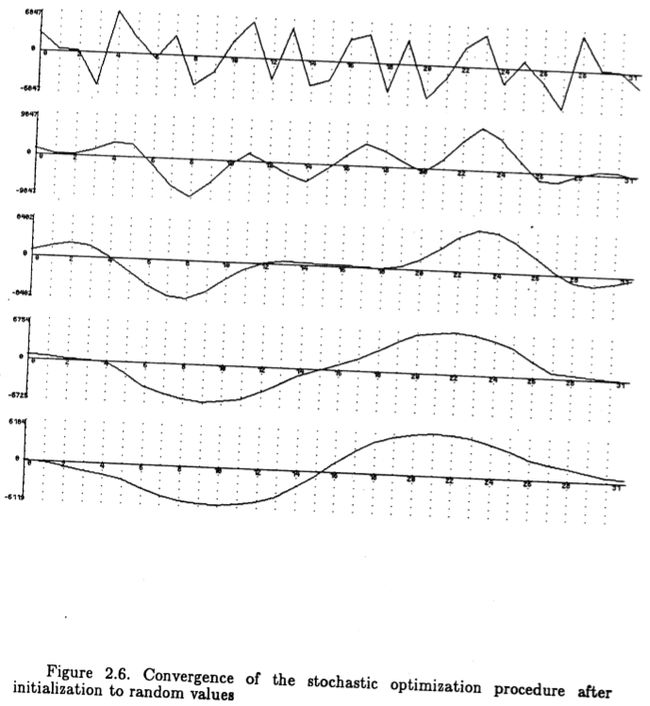
图（2.5）显示了在将滤波器初始化为不同的盒子之后，算法收敛到一个解。 在图（2.6）中，初始滤波器系数是随机且独立的。 值得将图（2.5）与图（2.3）进行比较，图（2.3）显示了算子在各种最大距离之间的最佳解析形式。 似乎随机方法以这样一种方式在参数空间中移动，即它在达到全局极值之前先经过了这些解析最优形式中的几种。 两种方法产生的解决方案相似，即使它们的标准略有不同。 有力的证据表明，最佳检测器的形式相对于准则的实际选择是可靠的，只要准则同时取决于错误率和定位能力即可。 在后面的章节中，我们将在Shanmugam等人（1979）的工作中看到更多的证据。
图2.5：随机优化过程在初始化后收敛到不同的盒子
图2.6：初始化后随机优化程序收敛到随机值
3.二维及以上
在一个维度上，我们可以使用一个位置坐标来表征空间中的阶梯边缘。在二维中，边缘也具有方向。在本章中，我们将使用“边缘方向”一词来表示边缘在二维中定义的轮廓的切线方向。假设我们希望检测特定方向的边缘，为此我们创建了一个二维蒙版。通过将垂直于边缘方向对齐的线性边缘检测函数与平行于边缘方向的投影函数进行卷积来确定方向。如果投影函数是与（的一阶导数相同的o的高斯分布，则可以大大节省计算工作量）高斯用作检测函数，可以通过将图像与对称的二维高斯进行卷积然后对边缘方向的法线进行微分来创建这样的遮罩，实际上，我们不必对每个可能的边缘方向的法线进行微分，因为光滑表面在任何方向上的斜率都可以根据其在两个方向上的斜率精确确定，检测器的最简单形式就是使用此方法。
在将图像与对称高斯卷积之后，从平滑的图像强度表面的梯度估计边缘方向。然后在该方向上非最大程度地抑制梯度大小。有向非最大抑制等同于以下非线性差分谓词的应用
其中S = G * I，其中I 是图像，G是对称高斯。 这很容易通过替换来解决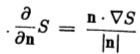
在（3.1）中被证明使用的非线性二阶导数算子的形式与Havens和Strikwerda（1983），Torre and Poggio（1983）和Yuille（1983）提出的形式相同。 在边缘增强的背景下，它也出现在Prewitt（1970）中。
通过在边缘方向上的二阶导数中找到零交叉点，该算子实际上可以找到最大值或最小值。原则上，通过首先将图像与对称的n维高斯卷积，可以将该运算符用于以任意数量的维度实现边缘检测器。由于高斯可分解为n个线性滤波器，因此使用n维高斯进行卷积非常高效。
使用平滑投影功能（例如高斯）还有其他更紧迫的原因。当我们将线性算子应用于二维图像时，我们在输出的每个点上形成一些输入值的加权和。对于此处描述的边缘检测器，该总和将是边缘不同侧面的局部平均值之间的差。在非最大抑制之前，此输出表示图像的一种移动平均值。从概念上讲，我们希望使用无限的投影函数，但实际边缘的范围有限。因此，有必要使投影函数窗口化（请参见Hamming 1983）。如果窗口功能突然被截断（例如，如果它是矩形的），则由于该窗口的带宽很高，因此滤波后的图像将不平滑。该结果类似于傅里叶理论中的吉布斯现象。当应用非最大抑制时，这些变化将趋向于产生“飘移”或在严重情况下甚至不连续的边缘轮廓。
解决方案是使用平滑窗口功能。在信号处理中，使用的典型窗口是汉明和汉宁窗口。高斯是这两者的合理近似值，并且对于给定的空间宽度，它肯定具有非常低的带宽（高斯是具有最小带宽和频率乘积的唯一函数）。对于较大的操作员规模，窗口功能的效果变得非常明显，这可能是在Marr和Hildreth在高斯拉普拉斯算子上进行工作之前，具有大量支持的操作员才是不实际的最大单一原因。敏锐的读者可能会看到投影函数中这些平滑性约束之间的相似性，以保持轮廓在边缘方向上的连续性，而检测函数的平滑性则由多重响应约束的添加所隐含。
在这里有必要将这种有向二阶导数算子的性能与拉普拉斯算子进行比较。首先我们注意到，二维拉普拉斯算子可以在两个任意正交方向上分解为二阶导数的分量。如果我们选择在主梯度方向上采用导数之一，则会发现运算符输出将包含一个与上述运算符基本相同的贡献，以及一个沿边缘方向对齐的贡献。第二个成分对定位或检测没有任何帮助（表面在该方向上大致恒定），但会增加输出噪声。这将在第7章中进行分析验证。
使用高斯卷积后再进行定向非最大抑制的一种检测器已经实现并执行得很好。 其输出示例将在第6章中给出。虽然完整的检测器包括多个操作员宽度，方向和长宽比，但它们是简单检测器中使用的操作员的超集。 在典型的图像中，大多数边缘由宽度最小的算符标记，而大多数则由非伸长的算符标记。 但是，正如我们将在以下各节中看到的那样，在某些情况下，应使用更大或更多个定向运算符，并且在适用时它们可以提供更好的性能。 使这种复杂的检测器产生相干输出的关键在于设计有效的决策程序，以便在图像中每个点之间的操作员输出之间进行选择。
3.1 需要多种宽度
在确定了操作员的最佳形状之后，我们现在面临选择操作员宽度的问题，以便在特定应用中提供最佳的检测/定位权衡。 通常，信噪比对于图像内的每个边缘将是不同的，因此在该方案中将需要合并几个宽度的运算符。 必须由算法动态决定使用哪个运算符，这需要在候选边缘周围的区域中对噪声能量进行局部估计。 一旦知道了噪声能量，就将知道每个操作员的信噪比。 如果然后使用噪声的概率分布模型，则可以有效地计算候选边缘为假边缘的概率（对于给定的边缘，此概率对于不同的运算符宽度将有所不同）。
由于先验地与错误地凹入的边缘相关联，而与边缘强度无关，因此，根据错误的概率而不是响应的大小对检测器输出进行阈值化是合适的。 一旦设置了概率阈值，就可以确定最小可接受的信噪比。 但是，可能会有几个操作员的信噪比高于阈值，在这种情况下，应选择最小的操作员，因为它可以提供最佳的定位。 我们可以对阈值的设置保持保守，因为最小的运算符错过的边缘可能会被较大的运算符拾取。 实际上，由于选择了较高的信噪比阈值会导致较低的错误率，因此仍然保留了错误率和定位之间的权衡，但是由于从较小的操作员处记录的边沿较少，因此倾向于提供较差的定位。
总而言之，在操作员输出之间进行选择的第一种启发式方法是，每当操作员有足够的
时，都应使用较小的操作员宽度。这类似于Marr和Hildreth（1980）提出的在高斯通道的不同拉普拉斯算子之间进行选择的选择标准。 在他们的情况下，该论据基于以下观察：较小的信道具有较高的分辨率，即来自相邻边缘的干扰的可能性较小。 该论点在当前情况下也非常重要，因为迄今为止，尚未考虑给定的操作员支持中有多个优势的可能性。 有趣的是，Rosenfeld和Thurston（1971）在选择纹理边缘检测算子时提出了完全相反的标准。论据是，较大的算子可以提供更好的平均，因此（大概）可以提供更好的信噪比。
以此为出发点，我们需要形成一个本地决策程序，当邻居中的几个操作员响应时，我们可以决定是否标记一个或多个边缘。 如果信噪比高于阈值，则应立即在该点标记一个边缘。 现在我们面临的问题是，几乎肯定会有较大的运算符标记的边，但是这些边可能不会与第一个边恰好重合。 对此的可能答案是抑制所有附近操作员的输出。 这具有防止大通道对叠加在锋利边缘上的“ 模糊” 边缘作出响应的不良效果。
取而代之的是，我们使用“特征合成”方法。首先标记最小运算符的所有边缘。根据这些边缘，我们合成了较大的运算符输出，而不是图像中仅有的边缘。实际的运算符输出到合成输出仅当大型运算符的响应比我们从合成输出所预测的要大得多时，才标记其他边。产生合成输出的最简单方法是采用由小运算符标记的边并在特定方向上与该算符垂直于边缘方向的高斯进行卷积，该高斯的
应与大通道检测滤波器的相同。
可以重复应用此过程，首先标记第二个最小比例尺的边缘，而第一个最小的边缘没有标记，然后从第三个比例尺中找到前两个标记中的任意一个都不标记的边缘。因此，我们建立了通过在每个比例尺上未用较小比例尺标记的边缘相加来创建累积边缘图。结果表明，在许多情况下，大多数边缘将由最小通道拾取，而较后的通道则主要标记阴影和阴影边缘或纹理区域之间的边缘。
3.2 对定向运营商的需求
到目前为止，我们已经假定投影函数是一个高斯函数，与用于检测函数的高斯函数具有相同的。 实际上，随着投影功能的长度增加，操作员的检测和定位都得到改善。 现在，我们针对操作员信噪比证明这一点。 本地化的证明是类似的。 我们将考虑在x方向上穿过原点的阶梯边缘。 该边缘可用等式表示
其中
是单位步长函数，A 是边缘的振幅，如前所述。 假设存在每单位面积均方值
的加性高斯噪声。 如果我们用一个脉冲响应为 f（x，y）的滤波器对该信号进行卷积，则对边缘的响应（在原点处）为
仅对噪声的均方根响应为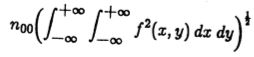
信噪比是这两个积分的商，用A表示。我们已经看到，如果将函数垂直缩放到边缘（方程2.13），会发生什么。 现在，我们通过替换
对投影函数f（x，y）执行相同的操作。 积分变成
两者之比现在为
。本地化
也提高为
。显然希望我们使用尽可能大的投影函数。对此显然有实际的限制，特别是图像中的所有边缘都是有限的，很少是完全线性的。但是，大多数边缘会持续一段距离，实际上比大多数边缘算子的3或4像素支撑要远得多。即使是弯曲的边缘，也可以通过足够小的比例的线性段来近似。考虑到这些优点，显然最好在任何适用的情况下使用定向运算符。唯一的条件是检测方案必须确保仅在图像适合线性边缘模型时才使用它们。
本算法通过形成拟合估计的良好性来测试每个方向性掩模的适用性。它在计算遮罩本身的同时执行此操作。形成长方向性遮罩的一种有效方法是对具有相同方向的未拉长遮罩的输出进行采样。该输出在平行于边缘方向的直线中以固定间隔采样。如果样品靠得很近（相距小于2），则所得的遮罩在其沿边缘方向的大部分范围内基本上是平坦的，并且在其端部会平滑地降至零。这种面罩的两个横截面如图（3.1）所示。在该图中（与本实施方式相同），操作员支持上有五个样本。
与掩模的计算同时，可以通过简单的平方误差度量来建立拟合的优度。由于估计生产面罩的数量是一些值的平均值，因此平方误差就是这些值的方差，然后我们消除那些方差大于平方输出的某个分数的算子输出。如果没有定向算子在一点上具有足够的拟合优度，则该算法将测试较少定向算子的输出。这种简单的拟合度优度足以消除传统上困扰定向运算符的问题，例如对高度弯曲的边缘的错误响应以及边缘超出拐角的扩展，请参见Hildreth（1980）。
投影函数的这种特殊形式，即在某个范围内具有恒定值的函数，该函数在两端大约用两个半高斯衰减到零，这与汉宁窗的常用扩展非常相似。后一种功能在一段距离上是平坦的，并在两端用两个半余弦铃逐渐衰减为零（BingHam，Godfrey和Tukey 1967）。因此，我们可以期望它作为移动平均估计器具有良好的属性，正如我们在本章开始看到的那样，它是投影函数所扮演的重要角色。
图3.1方向阶梯边缘（a）平行于边缘方向的横截面，（b）垂直于边缘方向的横截面，（c）多个掩模的二维脉冲响应
定向算子的设计中要做的所有工作就是确定方向数，或者等效地确定两个相邻方向之间的角度。为了确定后者，我们需要确定方向性操作符的角度选择性，该角度选择性取决于边缘方向和操作符的首选方向之间的角度0。假设我们通过取 2N + 1 个奇数样本构成算子。令样本数为n，其中 n 在 -N ... + N 范围内。回想一下，方向算子是通过与对称高斯卷积，垂直于算子的首选边缘方向微分，然后沿首选方向采样而形成的。区别表面将是与优选边缘方向成
角的脊。它的高度将随cos的变化而变化，第n个样本距脊中心的距离将为 nd sin
，其中d是样本之间的距离。归一化的输出将是
如果存在m个操作员方向，则两个相邻操作员的首选方向之间的角度将为180 / m。因此，边缘与最近的首选操作员方向之间的最坏情况角度为90 / m。在当前实现中，d / 的值约为1.4，有6个操作员方向。的最坏情况是15度，在这种情况下，操作员的输出将降至其最大值的85％。
3.3 噪声估计
为了估计来自操作员输出的噪声，我们需要能够将其对噪声的响应与阶跃边缘引起的响应分开。由于系统的性能将严重取决于此估计的准确性，因此也应将其表述为优化。维纳滤波是一种最佳估计两分量信号中一个分量的方法，可以在本应用中发挥优势。它需要了解两个组件的自相关函数以及组合信号。一旦噪声成分被最佳分离，就将其平方并进行局部平均。实际上，我们可以在平滑阶段进一步改善分离效果，因为当我们使用噪声估计时，我们会将其与边缘检测算子在局部最大值处的响应进行比较。 我们知道在检测算子的中心附近有一条边，并且该边将在噪声分离滤波器中产生一个已知的响应（噪声分离不会很完美）。 我们可以使用两个响应的位置对应关系，使局部平均滤波器由于其中心处的阶跃边缘而与输出正交。 理想情况下，当不存在噪声时，它应在边缘中心给出零输出。
令 g1（x）为我们要检测的信号（在这种情况下为噪声输出），g2（x）为某些干扰（边缘响应），然后将g1的自相关函数表示为R11
，将g2 的自相关函数表示为R22 ，它们的互相关为R12，其中两个实函数的相关定义如下
在这种情况下，我们假设信号和干扰是不相关的，因此R12 =0。最佳滤波器为K（x），其中K定义如下（Wiener 1949）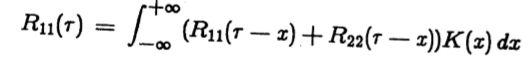
由于响应白噪声的滤波器输出的自相关等于其冲激响应的自相关，我们有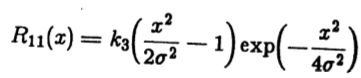
g2是在（2.38）中推导的运算符对阶跃边缘的响应，则我们将得到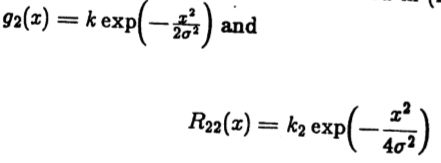
在边缘的幅度比噪声大的情况下，R22+ R11近似为高斯，R11是相同的高斯的二阶导数。 那么，K的最佳形式是增量函数的二阶导数。
上面的滤波器K与边缘检测算子的输出进行卷积，结果取平方。 下一步是平方噪声值的局部平均。 平均滤波器基本上是广义的高斯滤波器，但是在此应用中，通过将其与阶跃边缘响应正交可以提高其精度。 让平均滤波器表示为 A1（x）-A2（x）其中
A2表达式中的与检测过滤器相同。 （实际上，A2的最佳形状是高斯二阶导数的平方，但是使用此函数使该方案对检测滤波器最大位置的微小变化非常敏感）。 选择常数a1和a2，使得对平方滤波后阶跃响应的净响应为零，即。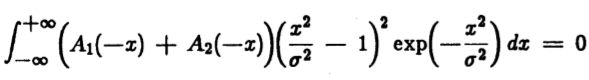
在对每个点的本地噪声能量进行估算之后，我们现在可以解决设置操作员阈值以实现最小错误率的问题。这是下一部分的主题。
3.4 滞后阈值
迄今为止，几乎所有的边缘检测方案都使用某种形式的阈值处理。 如果阈值不是先验固定的，而是由算法以某种方式确定的，则称检测器采用自适应阈值。 唯一的例外是Marr Hildreth方案，其中在高斯滤波器的拉普拉斯算子的输出中，在任何零交叉处标记边缘。 这是不切实际的主张，因为即使噪声具有消失的能量，对纯噪声的响应也具有非常高的过零密度。 此方案的大多数实际实现都使用基于零交叉的斜率的阈值处理。
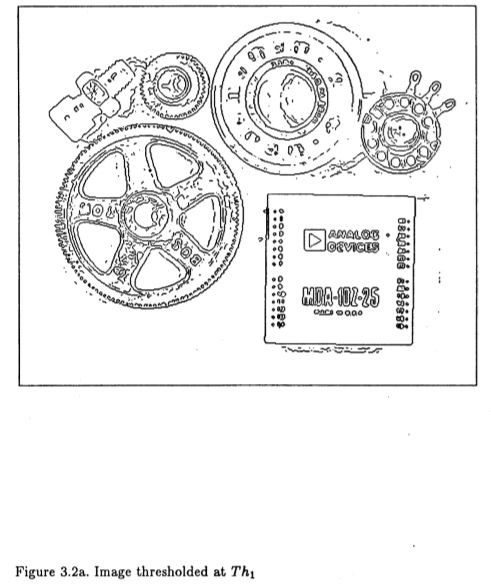
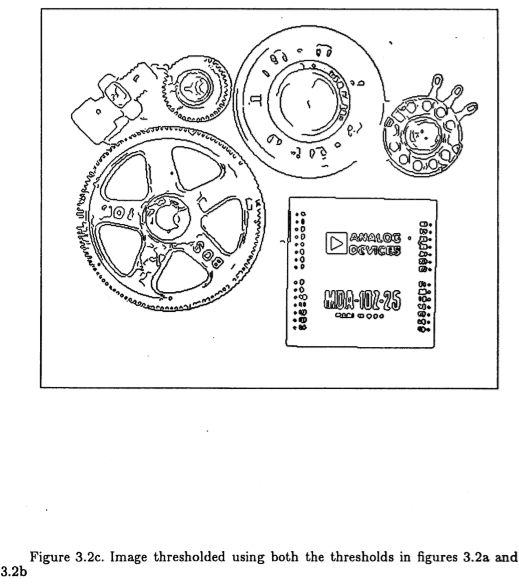
本算法基于图像噪声的局部估计来确定阈值，因此属于自适应阈值算法的类别。它具有额外的复杂性，它需要两个阈值来处理条纹问题。条纹是由于操作员的输出沿着轮廓的长度在阈值之上和之下波动而导致的边缘轮廓破裂。假设我们在Ath 处设置了一个阈值，并且图像中存在一个边缘，以便操作员以Ath 的平均输出幅度对其进行响应。即使噪声是非常轻微。我们期望轮廓仅在暂停时间左右才高于阈值。这会导致边缘轮廓破裂。虽然这是一种病理情况，但在阈值边缘检测器中，条纹是一个非常普遍的问题。设置这样的阈值是非常困难的，以便在保留高灵敏度的同时标记噪声边缘的可能性很小。图（3.2）给出了具有滞后的阈限效应的例子。
图3.2a：Th1阈值处的图像
图3.2b：图像阈值为2 Th1
图3.2c：同时使用图3.2a和3.2b中的阈值对图像进行阈值处理
Pentland（1982）与Mar Hildreth 过零点一起使用的对此问题的一种可能解决方案是，在轮廓的一部分长度上平均轮廓的振幅。如果平均值高于阈值，则标记整个段。如果平均值低于阈值，则轮廓中不会出现任何部分。通过以最大曲率断开轮廓来分割轮廓。在零交叉的情况下，这种分割是必要的，因为零交叉始终会形成闭合轮廓，显然这些闭合轮廓并不总是与图像中的轮廓相对应。
在当前算法中，未尝试对分段进行预轮廓。取而代之的是通过滞后进行阈值处理。如果轮廓的任何部分都高于高阈值，则立即输出该点，轮廓的整个连接段也将被输出，包含该点且位于低阈值之上。产生条纹的可能性大大提高，因为要使轮廓破裂，它现在必须在高阈值之上和低阈值之下波动。另外，由于可以提高高阈值而不会冒偷装的危险，因此降低了误食的可能性。高阈值与低阈值之比通常在二或三比一的范围内。
3.5 对平滑渐变的敏感度
在Binford-Hora（1973）中已经指出，图像经常包含缓慢的梯度，并且对这些梯度敏感的边缘检测器易于在梯度较高的区域中标记多个边缘。 上一章中得出的边缘算子对图像梯度很敏感，我们现在应该问是否有可能在不影响性能的情况下消除这种敏感性。 一种可能性是使用算子，该算子是最优算子的两个不同宽度的线性组合，使得所得算子对梯度不敏感。 假设函数f 由
然后我们发现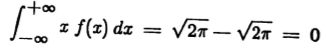
因此，该函数当然对梯度不敏感，其性能将由公式（2.12）给出。 现在信噪比和本地化
随着2趋于无穷大，上述表达式趋于极限值
与方程（2.40）给出的高斯简单一阶导数具有相同的总体性能。实际上，使用大约31 的2 值可减少计算费用，并防止操作员由于其强大的支持能力而对附近的边缘变得过于敏感。在这种情况下，整体性能EA
30％。还要注意，当2接近1时，我们获得了高斯的三阶导数，类似于有时用来估计Marr-Hildreth过零强度的算子。但是在这种情况下性能会降低，如第7章所示。
f 对梯度不敏感的事实意味着f 可以表示为平均值为零的函数g 的导数，并且函数f是对称的，因为f是反对称的。如Binford（1981）所述，可以将平均值为零的对称函数g 视为横向抑制算子。提出了侧向抑制作为降低梯度敏感性的机制。但是，横向抑制算子的形式实际上并不能直接影响性能，因此无法通过分析确定。
4 查找线条和其他特征
本书的第二章和第三章详细介绍了高米噪声阶跃边缘的最优算子的推导。 该运算符的解析形式的推导是相当繁琐的，最后，我们到达了参数形式，不得不求助于数值方法来找到参数a的最佳值。 寻找操作员的另一种方法是通过蛮力随机优化，甚至不使用解析表达式来确定最优性。 后一种方法更易于实现，但解决方案花费的时间更长，从理论上讲更普遍，因为找到一个针对不同输入波形的算子，只需更改其边缘模型即可。 尚未尝试过，修改随机优化器并获得解决方案所需的时间花费似乎没有道理。
如果有一个更通用的方法可以提供快速解决方案，并且易于适应新波形，那将非常有用。考虑针对其他功能的最佳检测器有几个原因。首先，已经指出（Herskovits和Binford 1970，Marr 1976），阶跃边缘不是发生的唯一强度变化，而是重要的。他们特别提到“屋顶”和“条形”轮廓在实际图像中很常见，这些轮廓在寻找最佳检测器时都会带来新的问题。
即使我们正在考虑台阶边缘轮廓，也可以为使用非白色高斯噪声模型提供强有力的理由。我们可以消除频谱平坦度约束，并且仍然可以使用相同的设计技术，只要可以将噪声建模为响应白高斯噪声的某些滤波器的输出即可。实际上，如果我们知道随机过程的自相关，则可以推导具有相同自相关的因果滤波器（线性预测变量）。通过将此滤波器的逆应用于要检测的噪声波形，我们获得了一个不同的波形，但是现在它陷入了白高斯噪声中。我们可以对新波形应用相同的设计技术，原始波形的最佳检测器是滤波后的波形和逆噪声滤波器的卷积。因此，我们已经将在非白高斯噪声中找到阶跃边缘的问题映射到了在白噪声中寻找其他边缘轮廓的问题。
4.1 标准的一般形式
当我们在第二章中得出台阶边缘的分析标准时，只有两个地方的输入波形形式实际影响了标准。 通过插入通用特征代替阶梯边缘，我们可以轻松获得通用准则。 回想一下，信噪比E的定义是操作员对输入波形和仅对噪声的响应的商。 对于具有脉冲响应f（x）的算子，噪声的响应将由公式（2.4）给出，即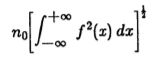
该运算符在任意波形 F（x）的“中心”处的响应类似于公式（2.3），仅
所以 f 和任何特征 F 的信噪比是（假设n0 = 1）
确定算子本地化的方法也与第2章中使用的方法类似，在此我们将不对其进行完整描述。 回想一下，定位被定义为标记边缘相对于真实边缘位置的标准偏差的倒数。 为了在操作员响应中找到最大值，我们实际上在其响应的导数中定位零交叉。本地化定义为微分响应中零交叉斜率与均方根噪声的商。 后者由公式（2.7）给出并具有值
差异化运营商响应的斜率是
因此，本地化
变为（假设n0 = 1）
现在可以将复合准则的最终形式写为（4.1）和（4.2）的乘积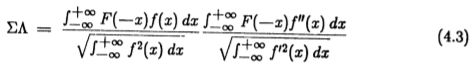
因此，找到一个任意的特征检测器需要最大化这个功能，可能会受到一些辅助约束的影响，例如多重响应约束（2.25）。 即使特征F是特别简单的，例如阶梯边缘，这通常也很难。 然而，功能（4.3）的形式非常简单，以至于给定候选特征检测器，我们可以容易地通过分析来评估其性能。 如果操作者冲激响应f 和特征F 都表示为采样序列，则（4.3）的评估仅需要计算序列之间的四个内积。
这表明可以直接对采样的算子脉冲响应进行数值优化。 可以预期该方法比随机优化要快得多，因为对性能的评估是精确的，并且可以准确地估计函数空间中每个点的梯度。 同时，非常普遍的是，对任何波形的优化仅需要波形的采样版本。
对于操作员而言，输出将不是解析形式，但是针对感兴趣特征的检测器的实现将始终需要离散的点扩展函数。 也可以通过使用惩罚方法来添加其他辅助约束（请参阅Luenberger 1973）。 在这种方法中，约束优化被简化为一个（或可能是几个）无约束优化。 对于每个约束，我们定义一个惩罚函数，当违反其中一个约束时，惩罚函数的值将为非零。 然后，我们找到最大
其中P是仅当违反约束时才具有正值的函数。 ui的值越大，满足约束的可能性就越大，但是与此同时，该方法变得病态的可能性就更大。可能需要使用ui值序列，每个优化的最终值都将用作下一个的起始值。在每次迭代中增加u，以便减小 P（f）的值，直到“几乎”满足约束条件为止。
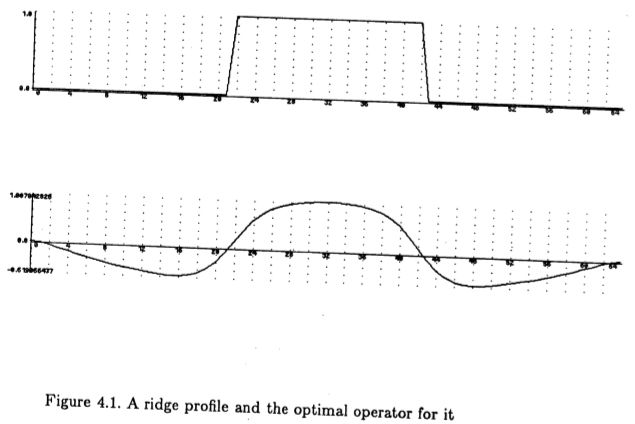
图（4.1）中显示了一个用于解决“山脊”轮廓问题的方法的例子，山脊的函数F被定义为一个宽度为w的平坦平台，两端的步长过渡为零。辅助约束是
（i）多重响应约束。该约束直接取自方程式（2.25），因为它不依赖于特征的形式。
（ii）操作员的直流分量应为零，即恒定输入的输出应为零。
由于脊的最优算子也是对称的，因此它对恒定梯度的响应为零。这意味着它可以表示为有限范围函数的二阶导数，这反过来意味着可能存在经济的计算方法二维的多个方向的算子。
图4.1：脊轮廓及其最佳算子
该图显示了为同一功能派生的两个不同的运算符。这两个算子在可能的支撑大小上有所不同。第二个被约束在位于山脊宽度两倍的区域内，而第二个在支撑上是山脊宽度的三倍。第二个运算符的性能比第一个运算符的性能稍差。但是，它需要较小的支撑这一事实意味着它不太可能受到相邻特征的干扰。性能的这一方面在很大程度上取决于支持的宽度，但其他方面的性能则不然。因此，我们选择操作员支撑为脊宽的三倍，因为如果脊之间的距离等于脊宽，即，如果脊和谷具有相同的宽度，则在该宽度处将不会产生干扰。
由于操作员的宽度直接由脊的宽度决定，因此建议应使用多个宽度的操作员。然而，这在本实施方式中并未完成。使用这种脊模型，可以将宽脊视为两个紧密间隔的边缘，并且该实现中已经包括针对这些边缘的检测器。使用脊线检测器的唯一原因是图像中的脊线太小而无法由最窄的边缘算子有效处理。由于存在许多特征（例如划痕，裂缝或印刷品），这些特征导致仅几像素宽的离散轮廓而经常发生。
图4.2：屋顶轮廓和屋顶的最佳操作员
使用类似的过程找到屋顶边缘的最佳算子。这些特征通常出现在对象的两个平面的凹面连接处。结果如图（4.2）所示。同样，存在两个辅助约束，一个约束对多个输入，一个约束对恒定输入的零响应。请注意，这两个算子之间的区别本质上是它们与各自输入的“相似性”，我们可以从维纳滤波理论中预期到这一点。对于高斯白噪声信号，最佳的维纳滤波器只是时间反转信号。然而，滤波仅考虑信噪比，并且定位和多个响应标准对操作员施加了有效的平滑度约束。
屋顶边缘检测器尚未被并入当前边缘检测器中，因为发现理想的屋顶边缘相对较少。在任何情况下，脊形检测器都是理想屋顶检测器的近似值，足以应付它们。对于专门设计用于处理多面体图像的边缘检测器（例如Binford-Horn寻线器（1971）），情况可能有所不同。在这里，可能需要几个宽度的屋顶操作员来处理图像中不同的信噪比。
上面描述的方法已经被用来找到针对脊和屋顶轮廓的最优算子，此外，它成功地找到了第2章中推导的最优阶梯边缘算子。应该可以使用它来找到针对任意特征和最优算子的算子。步进操作器应对非白噪声。例如，检测“蓝”噪声（已通过完美微分器的不相关噪声）中的台阶边缘的问题减少了检测白噪声中的屋顶边缘的问题，因此，在这种情况下，台阶边缘的最佳检测器是最佳屋顶算子的导数，请注意，它与我们在此推导出的屋顶算子不一样，因为后者包括零直流响应约束，这对阶跃算子没有任何帮助。
4.2 二维
现在，我们面临将一维脊算子扩展到二维的问题。 与具有台阶边缘的情况一样，扩展部分是一个运算符，由垂直于山脊方向的检测函数和与其平行的投影函数组成。 如前所述，我们使用此遮罩垂直于边缘方向非最大程度地抑制了图像卷积的输出。 然后可以对最大点进行阈值化（具有滞后作用），并且可以将标记的山脊轮廓与边缘贴图组合在一起。
然而，在脊的情况下，要获得准确的脊方向的难度要大得多。没有像梯度方向这样的简单度量可以与法线对齐。的确，较大的主曲率将垂直于脊线方向，但即使从平滑的图像进行测量，其可靠性也要低得多。请记住，脊线检测器将在最小阶梯边缘算子的分辨率以下工作，因此平滑度将是轻微的。这表明有必要在每个点上使用多个定向遮罩，并选择最适合局部的遮罩。已经发现这是不适当的解决方案，因为当脊高度弯曲时，它的性能如此差，通常是印刷文本的情况。尽管高度定向的遮罩对于长的直脊具有优势，但它们不足以作为一般的脊检测器。
实际上，必须使用类似于曲率的量度。主曲率方向不能直接使用，不仅因为它是一种嘈杂的测量。脊的峰应在脊方向上大致平坦，但垂直于此方向高度弯曲。但是，在山脊的侧面上有些点是近似平面的。这里最大曲率的方向将是任意的。它很可能会平行于山脊方向，并且在该方向上可能会略有最大值，因此将标记山脊点。
为了防止标记这些错误点，有必要修改山脊方向估计，以便考虑到垂直于最大曲率方向的山脊的斜率。如果该点位于山脊的顶部，则该斜率大约为零，但对于山脊侧面上最大曲率可能平行于山脊方向的点，该法线的斜率（即此时的山脊面很大）。因此，我们不是使用最大曲率方向上的非最大抑制，而是使用最大化
其中
是n的法线，
是一些正常数。
因此，在曲率低的区域中，上述措施选择的斜率较大的方向，这是对脊侧面的点的正确行为。该方法已被使用，即使在困难的山脊数据（例如，精细打印的文本）上也表现得很好。第6章提供了在某些文本图像上的性能示例。
脊运算器使用非最大抑制的第二个问题是，它对理想脊的响应具有两个与其主峰符号相反的旁瓣。在真实的山脊的任何一侧都将标记出负的山脊或山谷，反之亦然。实际上，台阶边缘任一侧的脊检测器输出中也将存在最大值，显然这些点不应标记为脊。我们开始遇到集成不同功能的描述的问题，这比集成来自不同运营商的同类功能的数据要困难得多。图像中的典型特征将导致来自几种不同类型的特征检测器的响应，并且必须对哪个特征最能代表图像做出决定。
Marr（1976）较为详细地讨论了Teature集成的问题，他强调了产生强度变化的单个连贯表示的重要性，即“ Primary Sketch”。这并入了对几种特征的描述，包括边缘，宽条和细条。 Marr并未开发出用于组合任意特征的有效算法，而是将选择标准应用于每个点的特征检测器输出。实际上，两个特征检测器的响应在空间上可能并不完全一致，尚不清楚如何修改选择标准。在这种情况下，表面拟合是一种有用的技术，如Haralick（1983）的“地形学原始草图”中所示。在这里，每种可能的解释都与误差度量相联系，该误差度量反映了真实图像与建模表面之间的差异。描述每个图像点是误差最小的点。
目前，尚未令人满意地解决将脊描述与边缘检测器输出集成的问题。已经实现了第3.1节中描述的特征综合方法的一般化，并在某些图像上给出了可接受的结果，但不够鲁棒，无法普遍使用。在组合运算符输出的情况下，总是优先考虑较小的运算符，并且特征合成始终沿一个方向进行。对于合并特征描述，在没有先验理由偏爱一个特征而不是另一个特征的情况下，应该对称。
例如，假设脊检测器和台阶边缘检测器都对大致为台阶边缘的特征做出响应。从边缘检测器标记的边缘点，我们合成了如果图像实际包含阶跃边缘会发生的脊检测器输出。然后，将脊检测器的输出与合成输出进行比较，如果不明显大于脊输出，则不会标记脊点。类似地，根据脊检测器的输出，我们重建了边缘检测器的输出，如果脊检测器准确地描述了图像，该边缘检测器的输出就会发生。边缘检测器输出（在此示例中）将比合成输出强得多，因此将标记一个边缘点。该方法的优点在于，可以在图像的一点上标记多于一种类型的特征的出现。已经发现这样的点确实出现在图像中（Herskovits and Binford 1970），特别是屋顶边缘经常叠加在台阶变化上，类似于山脊的“边缘效应”也经常伴随台阶变化。
由于检测器可能会在图像中的单个特征附近输出两种解释，因此有必要将脊和谷视为不同的特征。 必须使用某种形式的集成技术，例如特征综合或拟合优度测试。 在本实施方式中尚未做到这一点，本实施方式仅将这些特征之一与阶梯边缘图集成在一起。 这是一个仍有很多工作要做的领域，需要尝试几种功能集成技术。
5.实施细节
任何边缘检测器的最终测试都是其在真实影像上的某些应用中的性能。将派生的运算符转换为程序并非易事。尽管该程序的运行版本实际上很小，但仍是许多改进的结果。与前四章介绍的理论分析一样，这些改进也是边缘检测器设计的一部分。本章的目的不是描述任何此类程序。它将以抽象的方式描述几种算法，以实现边缘检测器所需的某些处理。作者认为这是必要的，原因如下：
（i）由于边缘检测器涉及大量计算，尤其是卷积运算，因此，要在合理的时间内运行，必须使用有效的算法，这一点很重要。
（ii）由于图像可能包含非常精细的细节，因此重要的是，本地操作涉及最少的像素数，但要提供最佳的像素精度。这尤其适用于诸如方向导数的计算和非最大抑制之类的操作。
（iii）边缘检测器不是视觉程序。 实现者应记住，检测器只是更大系统中的第一级，并应考虑选择其输出的表示形式。
本章将不会详细描述本边缘检测方案的所有方面，实际上，所提供的某些算法甚至不构成该方案的一部分，而是可以在将来的实现中使用。 取而代之的是，它将着重于实现过程中两个或三个更关键的方面，特别是与高斯进行卷积的有效方法，以及非最大抑制方案的细节。 它将以用于该程序广泛使用的本地并行操作编程的控制抽象的细节结束。
5.1 离散化的影响
迄今为止，所有分析都假设图像是连续的可微表面，并且边缘算子同样是连续的函数。由于数字计算机上检测器的大多数实现都将离散滤波器应用于采样图像数据，因此有必要找到连续滤波器的精确离散近似值。考虑在采样之前应用于图像的平滑滤镜（如果有）的效果也很重要。为了防止采样信号中的高频成分混叠，必须使用平滑滤波器。假设使用离散滤波器对图像进行平滑，采样和卷积。通过卷积的关联性，这等效于使用平滑器和离散滤波器进行卷积的结果用滤波器对图像进行卷积。如果可以使用高斯平滑函数对图像进行平滑处理，则无需以该比例进行卷积。
用离散滤波器近似连续滤波器的最简单方法是采样前者。如果此方法成功，则必须确保采样不会引入锯齿。考虑形式为高斯滤波器的连续一阶导数
假设以
的间隔采样图像（对于离散卷积，还必须以该速率采样滤波器），则奈奎斯特频率为
。滤波器的有效带宽应小于该频率的一半，以防止混叠。 该滤波器的傅立叶变换为
截止频率为
，代入我们发现截止频率为
对于较大的w ，此函数永远不会达到零振幅，但确实会非常快地接近零。我们可以在该函数下降到最大值的0.01时设置有效截止频率。这限制了可用于给定采样率的o的小值。 
的最小值约为。实际上，这是本实施方式中最小的操作员。
当我们尝试用有限脉冲响应滤波器近似无限高斯时，就会出现第二个问题。再一次，我们可以利用一个事实，即瓜斯在空间域中非常迅速地衰减到零。在当前的实现中，高斯被截断为其峰值的大约0.001。这限制了（离散）脉冲响应中采样数与滤波器宽度的比值。该比率通常为8，例如，若要近似滤光片的为2.0，则必须使用至少16个样本。
最后，应该提到的是，有时有可能完全省去卷积步骤。如果的期望值远小于，则离散卷积是不实际的。但是，可以在采样图像之前使用连续滤波器（平滑滤波器）执行等效卷积。由于理论上无论如何都需要平滑步骤，因此不需要额外的计算工作。实际上，我们发现平滑功能决定了随后的边缘检测器的性能，而高斯平滑的使用应提供接近最佳的阶梯边缘检测。
5.2高斯卷积
看到一整节专门介绍看起来非常直接和具体的计算，也许令人惊讶。 但是，二维高斯函数有几个有趣的属性，这些属性建议了卷积的快速算法。 特别地，中心极限定理意味着，利用任何有限滤波器的重复卷积趋向于对高斯卷积的限制。 我们首先回顾离散卷积。
5.2.1 离散二维卷积
二次求和给出了带有二维滤波器 f（i，j）的离散图像 I（n，m）的卷积输出
假设滤波器f在两个维度上具有相同的尺寸M。 对于每个计算出的输出点，此方法需要M2个乘法，并且加法略少。 这是一种通用方法，可与任何二维有限脉冲响应滤波器一起使用。
5.2.2 使用一维分解进行卷积
现在我们考虑一种更特殊的卷积形式，它适用于二维滤波器的有限子类。 子类是可分离的二维过滤器的类。 该类的特征是将其脉冲响应分解为独立的线性滤波器
其中*表示卷积，并且滤波器fx 和fy 仅具有M个非零分量。 通过使用卷积的关联性，我们将带有二维滤波器的图像的卷积分解为带有线性滤波器的两个卷积
此方法仅需要2M乘法，并且每个点的加法次数大致相同。 对于较大的运算符大小（M的值通常为64），此方法比朴素的方法快得多，但仅限于可分离的滤波器。 此类的有用成员的数量实际上很少，高斯实际上是唯一可以以这种方式分解的二维对称函数。 其他有用的可分离函数包括高斯在x 和y 方向上的一阶导数。
5.2.3 递归过滤
到目前为止，我们已经使用有限脉冲响应滤波器来逼近无限高斯函数。 如果我们改为使用ininite脉冲响应（递归）文件，则近似值可能会更准确。 我们再次利用二维高斯的可分离性，从而可以将滤波器设计问题重新归因于设计近似高斯的一维滤波器的问题。 惯性脉冲响应（lIR）滤波器的特征在于
其中 x（n）和 y（n）分别是第n个点的输入和输出。该滤波器大致等同于具有P 极和Z 零的连续滤波器。极点的位置由系数bj 确定，而零点由ai 确定。
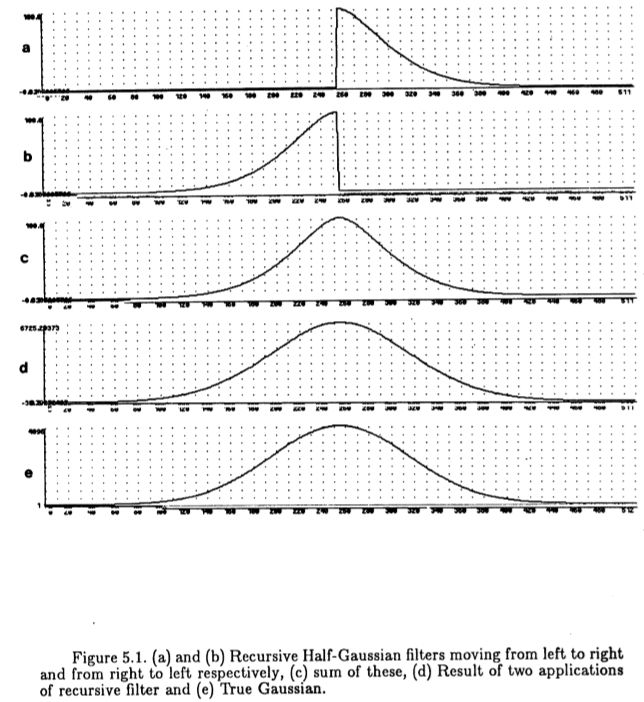
使用这种滤波器接近高斯滤波器的直接缺点是该滤波器“仅在一个方向上”是无限的，并且高斯滤波器具有在两个方向上都延伸到无穷大的脉冲响应。图（5.1）说明了这个问题的解决方案。我们使用两个沿相反方向移动的递归滤波器，每个递归滤波器的脉冲响应约为半高斯。然后，我们将两个响应相加（并减去中心点处的分量，该分量被加倍），并与对称高斯近似。如果我们希望对滤波后的图像重复此过程，并且（通过中心极限定理）我们将获得非常接近高斯的近似值，如图（5.1）的最后一帧所示。
图5.1：（a）和（b）分别从左向右和从右向左移动的递归半高斯滤波器，（c）这些求和，（d）递归滤波器两次应用的结果，以及（e）真高斯。
半高斯近似于阻尼指数余弦，在递归滤波器中需要两个极点和两个零。通过考虑响应的零交叉附近的四个离散输出值来得出b系数。我们选择的值是
将方程式（5.2）应用于前三个值和最后三个值，得出两个方程式，每个方程式仅涉及bj 之一，其解为
其中 a和w 分别是阻尼指数余弦响应的衰减常数和角频率。 a和w 的典型值为
其中是等效高斯的标准偏差。 ai 确定滤波器的增益及其在原点处的一阶导数。 对于单位增益和对高斯斜率的最佳近似，我们使用
该方法的有趣之处在于它的复杂度与无关。实际上，对于单步逼近，每个点仅需要12次乘法和加法（每个3次用于四个方向的滤波）。它还需要极少量的数组引用，并且可以通过将先前的 x和y 值保存在寄存器中来减少数量（仅需要三个）。每个点仅使用 4个参考即可实现该算法。实际上，通常最好在图像上进行两次通过，因此上述数字应加倍。
当然，此特定方法比以前的方法更加专业，并且仅对高斯函数和某些其他无限函数有用。但是，它具有所讨论的所有算法中最低的复杂性，并且在内存引用方面非常经济。另一个优点是，可以通过简单地更改某些参数的值来改变过滤器的大小，而不会影响算法的执行。对于将来的任何实现，它似乎都是首选。
5.2.4 多项式逼近
在最后两个小节中，我们看到了通过使用高斯的特殊属性，我们能够减少执行卷积所需的乘法次数。产生的算法不再是一般的卷积，而是局限于二维过滤器的子类。通过利用中心极限定理的全部能力，可以产生根本不需要乘法的算法。回想一下，使用任何受空间限制的滤波器进行的重复卷积都趋向于等效的高斯卷积。如果选择将两个相邻点相加的滤波器，并且重复多次相加，则无需乘法即可获得高斯近似。
该方法的一个有用类比是利用离散卷积和多项式乘法的等价性。由两个连续样本相加产生的滤波器与多项式（x + 1）相乘。如果应用n次滤波器，则相当于乘以多项式（x + 1）n。该多项式的系数由二项式定理给出。然后，我们使用以下事实：对于大的n，二项式分布可以由高斯近似。就乘法而言，该方法是经济的，但是其复杂度较高。由于在对卷积进行卷积时两个分布的方差相加，因此标准偏差仅随着卷积数的平方根增加。应用加法滤波器n次后的值为
为了用本节其余部分中的术语表述此结果，我们找到了等效离散卷积所需的样本数 M。 由于M通常为8，因此每点 n 的相加次数与等效蒙版大小之间的关系为
该算法用于二维卷积的总体复杂度（假设将其与分解配合使用）为每点
M2 加法，其中内存引用的数量大致相同。 这听起来像是一个非常大的购物中心编号，但是指数很高。 可能会使用的M 的最小值为8，因此使用此方法的最小加法数为18。但是，即使我们正在利用可分离性，加法的数量和内存引用的数量也会随M2 的增长而增加。。 由于浮点加法所需的时间通常不会比乘法的时间低很多，因此随着M的增加，此方法很快变得没有吸引力。
5.2.5 快速卷积
近年来，已经为整数多项式乘法开发了非常快的算法（Schonhage和Strasen 1971）。渐近算法的整数倍长度为 O（n）。对于卷积，我们通常使用比输入长度短得多的滤波器，因此我们应该期望卷积的渐近时间与滤波器长度无关。然而，试图达到渐近复杂性附近的任何地方，都会引入过高的常数。
但是，一切并没有丢失。通过使用最简单的快速乘法形式，我们可以以相对较低的开销获得非常有用的加速。考虑要卷积的两个数字序列。我们假设A的序列长度为2n，并将每个序列分为两个长度为n的子序列。假设两个序列分别为 x和y，并将子序列分别表示为 x1，x2和y1和y2。然后
其中
表示序列左移 n 。然后，我们使用卷积对加法的分布，我们有
由此看来，计算 2n个长度卷积需要4个长度为n的卷积，这意味着n2的增长顺序。 但是上面的表达式也可以写成
它只需要3个长度为n 的卷积，加上一些额外的加法和减法。 我们可以递归地应用该技术来计算这些较短的卷积，然后得出一种算法，其增长阶次小于n2。 这会导致执行长度为n 的卷积的乘法和加法的递归关系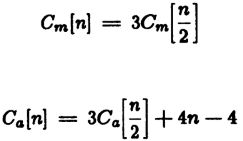
其中Cm是乘法数，Ca是n点卷积的加法数。 当这些递归得到扩展和简化时，我们获得了乘法和加法复杂度
其中L是大于或等于 log2（n）的最小整数。 为了将这些结果转换为长序列（例如长度n1）与短序列（长度n2）的卷积，我们假设n = n2。 我们将需要
个这样的卷积，每个卷积将需要
乘积，结果复杂度为
，因此，我们发现复杂度在较长序列的长度上是线性的，但仅随较短序列的平方根（大约）而变化。对于二维卷积，保持相似的结果，并且乘积精度为每点M1.2 乘积，而加法复杂度约为此乘积的六倍。
因此，我们得出了惊人的结果，该方法的复杂度几乎与一维分解的卷积相同，但是使用了完全通用的二维蒙版。该算法已实现，早期测试表明，它在n = 16 左右的天数卷积上开始表现出降低的复杂性。在n = 1024 时，加速是五至六倍。它可以在6n 空间中实现，并且内存引用的数量与添加的数量大约相同。
复杂度常数的低值使该方法比对n小于16000的值进行快速傅里叶变换的卷积更快（警告：此数字与硬件密切相关）。由于它具有自然的递归定义，因此它也比FFT编码容易一些。很可能这是对16到16000范围内的n进行一般卷积的最快方法。该方法可以使用具有最佳边缘检测算子形式的二维掩码，而不是高斯近似值。尽管快速卷积算法尚未被纳入边缘检测器中，但它确实值得进一步实验。
5.2.6 子摘要
希望本节强调了这样一个事实，即似乎有平凡的操作（例如卷积）经常有很多有趣的实现。但这还有另一个目的。在尝试解决视觉问题时，首要考虑应该是激励性的，即该算法应计算的内容。第二个是可行性，例如可以从图像中计算出什么。仅在处理了这两个问题之后，才应考虑到易处理性施加的任何约束，即可以在合理时间内计算出的约束。在对实现进行了很多考虑之前，并且仅当似乎没有高效的算法可用于计算时，才应考虑有效性的存在而影响算法的选择。这个主题是Marr（1976）的工作的特征，他运用上述考虑强烈地主张要解决图像处理问题。
5.3非最大抑制
最佳边缘算子是在以下假设下得出的：边缘将在其输出中标记为最大值。对于二维图像，找到这些方向最大值很简单，但是已经进行了各种非最大值抑制方案的大量实验。该操作应尽可能本地化，即应依赖于靠近潜在边缘点的像素，但操作也应鲁棒且准确。
这里描述的非最大抑制方案可以以两种方式之一使用。在第一种情况下，边缘方向是通过简单地在x和y方向上进行微分而从高斯平滑的图像表面的梯度中估算出来的。然后在梯度方向上非最大地抑制梯度大小。这只是方程式（3.1）的可能实现。在第二种情况下，该算法用于定向掩模输出的非最大抑制。在此，梯度方向是固定的，是操作员的财产。我们再次非最大地抑制梯度幅度，在这种情况下，梯度幅度是该算子的响应幅度。
图5.2：非最大抑制运算符的支持
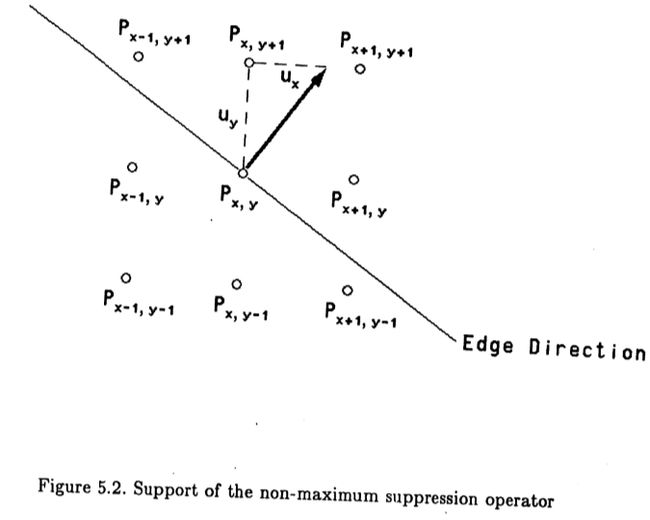
无论哪种情况，算法都是相同的。 它使用一个九像素的邻域，如图（5.2）所示。 边缘方向的法线（渐变或首选的操作员方向）显示为箭头，并且具有分量（ux，uy）。 我们希望非最大程度地抑制该方向上的梯度大小，但我们在点Pi，j 处仅具有离散的梯度值。 对于非最大抑制，我们需要三个点，其中一个将是Px，y，另外两个应是对向量u从Px，y 偏移的点处的梯度量的估计。
现在，对于任何u，我们都考虑Px，y在8像素附近的两个点，它们在u方向上最接近通过Px，y的线。 这两个点处的梯度大小与点Px，y处的梯度一起定义了一个平面，该平面切开了这些点处的梯度大小表面。我们使用该平面局部近似曲面，并估计直线上某个点的值。 例如，在图（5.2）中，我们估计在线上Px，y+1 和Px+1，y+1 之间的一个点的值。 插值梯度的值为
类似地，在Px，y的对侧上的一点的插值梯度为
如果G（x，y）> G1 和 G（x，y）> G2，则将点Px，y 标记为最大值。插值在其他梯度方向上相似，并且将始终包含一个对角线和一个非对角线点。实际上，我们可以通过乘以uy 来避免除法。
该方案每个点涉及五个乘法，但这并不过分，并且比将点Px，y 与两个邻居进行比较的简单方案要好得多。它也比使用沿边缘的梯度平均值而不是仅使用Px，y 的平均值的方案更好。
5.4 映射功能
在本章结束时，我们将简要讨论图像处理算法程序结构的一般方法。低级视觉程序的开发需要在图像的每个点上进行很多重复的操作。这些计算的结果之间将存在一些依存关系，这意味着存在自然的（部分）计算顺序，并且必须计算某些中间结果并将其保存在某处。除了对硬件（或目标代码）的考虑之外，还有两种基本的方法可以为这种处理实现软件接口。
第一种也是最明显的方法是提供一组原始数组操作，例如加法或卷积，它们将数组作为参数并将结果存储到数组中。 使用这些原语编写的程序看起来像普通的顺序汇编代码，除非存在一些必须以非标准方式在数组上移动的复杂函数（从原语构建）。 在这种情况下，每次调用基元时都必须重复描述函数移动方式的参数。 这导致麻烦且非正交的代码。
第二种方法是提供一种映射函数，该函数将局部图像处理函数作为参数，并通过其他参数指定的运动将其移动到一定数量的数组上。 映射和本地计算的两个操作现在由单独的功能处理。这种方法使人联想到Lisp中的MAP功能（Moon，Stallman和Weinreb 1983），并且在哲学上与CLU中的迭代器概念相似（Liskov等人，1979）。 它在用户级别具有许多优势。 首先是本地函数可以用源语言编写，例如Lisp（即使映射函数将其转变为完全不同的东西）并可以在一组示例参数上进行测试，而无需生成测试图像。 源代码更紧凑，更不容易出错，并且主观上更具可读性。 如果可以使用并行处理硬件，则使用第一种方法，源代码将编译为类似代码的内容。 两种方法的执行效率不会有显着差异。
但是，对于连续加工，直接实施类似第二种方法的东西有具体的优势。由于局部功能在移至下一个之前会在一个点上进行完全评估，因此每个中间结果只需要一个存储位置。这与前一种方法形成对比，后者需要为每个中间结果存储一块数据。中间值可以保存在高速存储设备（寄存器或高速缓存）中，这大大减少了将功能应用于完整图像所需的内存访问次数。当局部函数使用条件分支时，还有非常大的加速可能，因此处理图像点的时间很大程度上取决于该点的数据值。对于（大多数）并行机，将功能应用于n点的时间将是单点应用的最坏情况。有条件的分支必须通过为要跳过的代码长度设置一个非执行标志来完成。稀疏数据或递归过滤等计算快捷方式无法利用。
根据作者的经验，后一种样式使代码开发变得更加容易（这是算法实现中的一个认真考虑，其中很多都是用Lisp机器微代码编写的）。在一定程度上是正确的，因为纯粹的代码量，某些较复杂的功能（例如稀疏的定向掩码）可能无法使用第一种方法来实现。边缘检测器已使用第一种方法部分实现，并完全使用了映射功能（已对其微码编码）。映射函数映射到任意数量的数组上，每个数组具有任意增量，并且如果要映射的函数返回多个值，则可以将结果存储到多个输出数组中。 两种方法之间的执行时间差异很小，但是第二种方法使用的数组存储量少得多，而源代码则短得多。
6 试验
已经强调，边缘检测只是视觉系统的第一步，检测器的性能只能在其上下文中进行评估。也有人争辩说，许多后来的模块的要求都与在某种程度上应该设计一种在几种情况下都能正常工作的检测器相似。从这个假设出发，我们基于一组精确的性能标准设计了一个探测器，这些标准似乎是这些后续模块所共有的。在第2章和第4章中，我们很难准确地捕捉到我们最初定义的“直观”标准。实际上不可能在有限的一组标准中捕获边缘检测的所有理想属性，并且在最终分析中，唯一有效的标准是检测器对真实数据的性能。本章涉及在实验级别评估性能，并将包括与其他一些边缘检测算法的比较。评估分为三个阶段：
（i）验证分析绩效标准。操作员经过精心设计，可以最佳地检测高斯噪声中的台阶边缘。它应该在步骤的综合图像上表现良好。
（ii）对真实图像性能的主观评估。这里的目的是验证算法的各个部分的操作，特别是对不同算子宽度和方向的集成。无法通过检查检测器的输出来验证它们，但是通常可以通过这种方式隔离其操作中的缺陷。也就是说，我们无法通过查看输出来判断检测器是否工作正常，但是我们可以确定检测器出现故障的地方。
（iii）在某些情况下评估探测器的性能。由于边缘检测器是许多视觉程序的第一步，因此比较边缘检测器是合适的，方法是比较使用两个检测器的程序的性能。如果最初的假设是许多视觉模块具有相似的条件是正确的，则使用这些标准设计的检测器应在所有模块上均表现良好。
最后，我们将展示一些人类视觉系统的简单演示，这些演示与此处介绍的边缘检测器一致。尽管这不能证明人类视觉系统执行了相同的计算，但确实表明这两个系统具有相同的目标集。它加强了性能标准的选择，并证明使用这些标准设计的边缘检测器可以在各种图像上表现良好。
6.1 噪声中的阶跃边缘
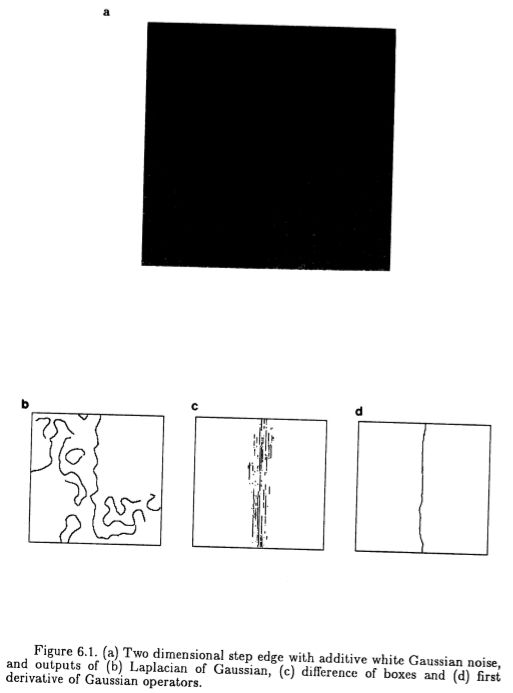
在第7章中，我们将证明有方向的二阶导数边缘算子在应用于高斯平滑图像时会比Laplacian更好地定位。我们还声称（第2章）盒算子的不同会给嘈杂的步幅带来不可接受的多重响应性能边缘。我们现在应该实验性地测试这些结果。在图（6.1）中，我们有一个二维阶跃边缘，具有加性白高斯噪声。连续的帧显示了盒子的差异，高斯的拉普拉斯算子和高斯算子的有向一阶导数的响应。图像的信噪比（定义为阶跃幅度与每个像素处的噪声标准偏差的比）约为0.2，图像的256 x256。Laplacian和一阶导数的高斯运算符的
均为8.0像素，而框掩码的x和y长度为32像素。
在卷积步骤之后，对盒运算符的差的输出的处理与有向一阶导数运算符是相同的，即，它是非最大的，并具有滞后阈值。 对于高斯的拉普拉斯算子，顺序略有不同。 首先在卷积输出中的零交叉处标记边缘，然后计算卷积输出的梯度，并使用磁滞对梯度幅度进行阈值化。
图6.1：（a）具有加性高斯白噪声的二维阶梯边缘。 （b）高斯的拉普拉斯算子，（c）盒子的差分和（d）高斯算子的导数。
对于每个操作员，都有两个根据经验设置的阈值以提供最佳的主观输出。 图（6.1）给出了每个操作员的定位和多重响应性能的指南。 正如我们所期望的那样，有向一阶导数算子在主观上要比拉普拉斯算子更好地定位，并且盒子的差异会响应单个边缘而产生多个轮廓。
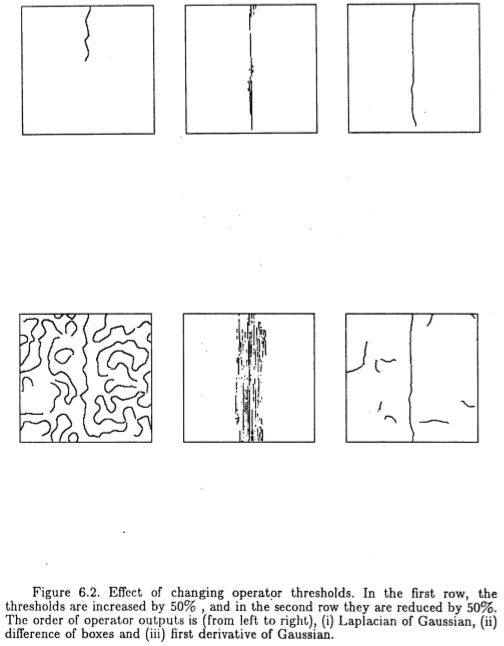
图6.2：更改操作员阈值的效果。 在第一行中，阈值增加了50％，在第二行中，阈值减少了50％。 运算符输出的顺序是（从左到右），（i）高斯的拉普拉斯算子，（i）方差和（ii）高斯的一阶导数。
为了对操作员的检测性能（即信噪比）有所了解，我们可以看到随着我们从最佳值更改阈值而产生的输出变化。 图（6.2）的第一行显示了将所有阈值提高50％的结果，在第二行中，阈值从最佳水平降低了50％。 从这些我们可以推断出箱形算子的差异具有最佳的信噪比，因为对于所有阈值水平，它仅在阶梯附近标记边缘。 当然，信噪比只是检测性能的一个组成部分，而缺乏多重响应的是另一个。 在这方面，盒子的差异表现非常差，并且随着阈值的降低而变差。 与其他两个相比，高斯的拉普拉斯算子显示出较差的信噪比，并且无法设置阈值，以便标记边缘轮廓的整个长度而不会由于噪声而引入轮廓。
可以说，可以通过对输出使用“修剪”启发法来规避高斯拉普拉斯算子或盒子运算符差异的问题。例如，可能会认为有可能消除“接近”边缘的盒子输出差异的错误最大值，或者使用高斯通道的不同拉普拉斯算子的输出来加强边缘的证据。这个论点没有讲到重点。当非最大抑制之后，此处导出的最佳算子或高斯近似的一阶导数为单个线性算子提供最佳性能。为了提高其他运算符的性能，必须应用非本地谓词，从某种意义上说，这会使滤波步骤变得多余。
6.2 操作员集成
我们认为，为了处理各种图像，边缘检测器应包含不同宽度的运算符。当适用时，我们还主张使用高度定向的蒙版。所有这些运算符都对相同类型的功能（一个阶跃边缘）做出响应，并且其中几个对相同的边缘做出响应时，检测器必须仅标记单个边缘。集成不同运算符输出的问题非常严重。实际上，许多反对方向运算符的论点都是务实的，即很难组合定向运算符并产生一致的输出。组合不同宽度的运算符输出的问题更加严重，因为响应单个边缘的两个运算符的输出最大值可能会与其他提示分开。第3章将特征综合描述为一种组合多个特征检测器输出的方法。该方法用于边缘检测器的实现中，现在我们探索它在某些测试图像上的性能如何。
6.2.1 不同掩模宽度的集成
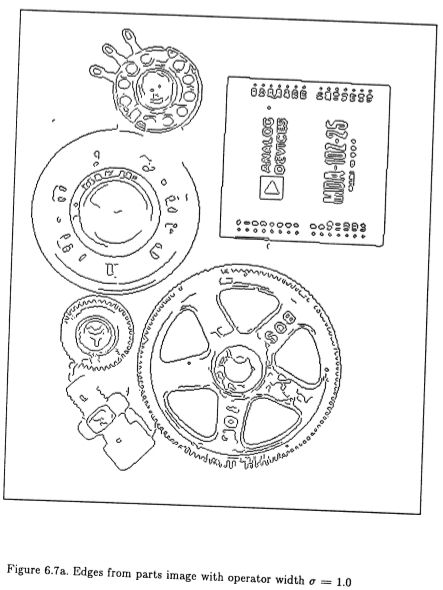
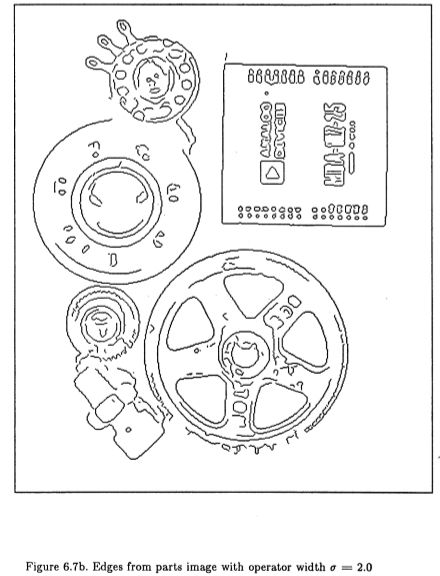
读者可以通过参考图（6.4）轻松了解图像中不同比例出现的各种细节。该图显示了在穿孔清洁布的图像上由两个操作员标记的边缘。遮罩宽度分别为= 1.0和= 5.0。这两个比例尺的边缘实际上是独立的。相比之下，图（6.7）在某些机械零件的图像上显示了用算符 = 1.0和 = 2.0标记的边缘。在此图像中，几乎所有细节都由较小的操作员拾取，并且仅在某些阴影边界上失败。这两个图说明了特征集成问题的实质。理想情况下，应标记图像中的每个特征，但只能标记一次。
图6.3：（a）清洁布图像
图6.4：（a）清洁布边缘的图像，操作员的宽度为（b）边缘清洁剂的 = 5.0
图6.5：（a）使用特征合成将清洁图像中的边缘合并，（b）两组边缘的叠加
图6.6：（a）零件图
图6.7a：零件宽度为 = 10的零件的边缘
图6.7b：零件边缘的图像，操作员宽度为 = 2.0
图6.8 a：使用特征综合的零件图像组合边缘
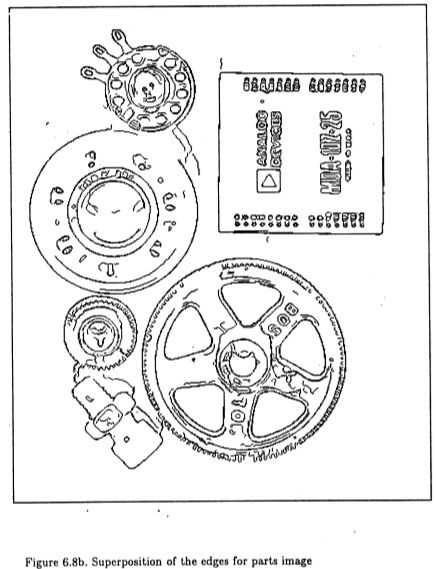
图6.8 b：零件的边缘重叠图像
我们的基本宽度选择标准，即使用具有足够信噪比的最小运算符，应该在零件图像上做正确的事情。首先将标记较小比例尺的边，然后将较大的算子输出进行合成，最后，将添加较大算子输出中与合成输出不一致的所有边。结果如图（6.8a）所示。此图与图形（6.7a）之间的唯一区别是添加了一些阴影边缘，并且扩展了某些阴影边缘。同样，图（6.5a）显示了图（6.3）中边缘的组合输出。由于较小的算子看不到图像中的长阴影线，因此不会合成与之对应的大算子特征。当它们出现在实际的大型操作员输出中时，它们会在检测器输出中标记出来。
特征合成方法在合成算子输出的“抑制”效果方面有一定的自由度。回想一下，要标记边沿，实际的运算符输出必须显着大于合成的输出。在本实施方式中，首先获取实际梯度与合成梯度之间的矢量差，并且如果该差的大小大于合成装置的磁通量，则标记新的边缘。通过将比例因子引入比较中，可以改变标记新边缘的可能性。该因素必须根据经验确定。上面的两个图像在因素上提出了相互矛盾的要求。如果太大，则会错过布料纹理中的模糊边缘。如果太小，则零件图像中会出现边缘点重复，从而导致边缘轮廓变脏。发现单个值，该值给出了两个图中所示的结果。为了进行比较，此值在所有尝试的图像上都给出了良好的结果，并且不需要对特定图像进行“调整”。为了进行比较，在图（6.5）和（6.8）中的每个组合边缘贴图下方是来自哪些地图已形成。
最后两点。 为了使特征合成在布料纹理图像上有效，应由较小的比例尺的边缘生成操作员，该操作员对慢梯度不敏感，如第（3.5）节所述。 否则，合成的大型运算符输出将包含一个缓慢变化的分量，即使小型运算符未标记慢速边缘，该分量也将防止标记新边缘。 这个分量是由于缓慢的梯度“泄漏”了较小的运算器的大量紧密间隔的边缘，通常来说，当两个特征独立时，特征合成最有效。
组合输出还显示出长轮廓的条纹。 这是因为当前使用单个比例因子来比较实际和合成输出。 可以将此因素视为一种阈值，因此应该通过使用两个值（即通过使用滞后进行阈值化）来改善性能。 在撰写本文时尚未对此进行尝试。
6.2.2 方向罩的集成
从第（3.2）节回想起，只要高度伸长的方向算子具有足够的图像拟合优度，它们是首选。 它测量的好处仅仅是沿定向遮罩的长度在几个点上的梯度值的标准偏差。仅当这些值的总和超过其标准偏差的某个固定倍数时，定向操作员才能标记边缘。 这样可以防止定向操作员对弯曲的边缘做出反应或使边缘轮廓超出拐角。
这也使操作员集成更加容易。 一方面，很少有两个以上的方向运算符响应特定方向的边缘。 同样，如果定向操作符产生的边缘点的宽度相同，则它们不会相对于较少定向操作符产生的边缘明显偏移。 这是因为，只有在边缘明显弯曲的情况下，才能移动边缘点，但这会立即阻止定向操作员对此做出响应。 特征合成对于定向算子集成不是必需的，并且简单的非最大方案就足够了。
图6.9：Dalek图像，大约700 x 500像素
Figure 6.10a.Edges from Dalek image ato=2.0
图6.10 a：Dalek的边缘， = 2.0
图6.10：Dalek图像在 = 2.0时的方向边缘，其中的算子在六个方向上
非最大抑制方案在第（5.3）节中进行了描述。对于定向算子，非最大抑制的唯一特性是，对于每个掩模，非最大抑制的方向是先验固定的。它垂直于面罩的长轴。一旦所有的边都被方向算符标记，就可以计算出简单的梯度幅度。复合梯度形成为简单梯度的最大值和方向梯度的大小。然后，该复合梯度在梯度方向上被非最大抑制。形成复合渐变的效果是防止将简单（非方向性）边缘标记为与方向性边缘相邻。图（6.10）给出了该方案的性能示例。 （6.10）的第一帧显示了使用简单梯度非最大抑制进行标记的边缘；第二帧显示了相同比例的方向算子的添加；第二帧中显示了多个其他拉长的边缘，没有拉直的迹象弯曲的边缘或边缘超出角的延伸。
边缘检测器已被作者在实际系统中广泛使用。其中第一个是轮廓跟踪器，该轮廓跟踪器可定位电视摄像机图像中的边缘轮廓，并为遵循该轮廓的机器人操纵器规划轨迹。第二个系统在机器人工作区的俯视图像中形成对象边界轮廓的多边形近似值。图（6.11）给出了该系统的一个例子。然后将这些用于规划通过工作空间的路径，以避免障碍。其他人也曾在形状描述中使用过它（Brady和Asada 1983）。 它已被用作Marr Poggio立体算法（Grimson 1981）的实现的前端，但在此应用中尚未与高斯零交叉的Laplacian进行定量比较。 检测器输出（如所承诺的）各种图像，这些图像显示在（6.12）至（6.15）中，图像全都约为700 x 500像素，并且在装有MIT Lisp的计算机上处理每个图像的时间约为10分钟 没有特殊的硬件。
图6.11（a）：某些纸张形状的图像，（b）从操作员宽度 = 1.0开始的边缘，（c）将多边形逼近边界
图6.12a：卡西莫多图片
图6.12b：Quasimodo图像的边缘，使用操作符宽度= 1.0，其中边缘强度由增加的亮度表示。
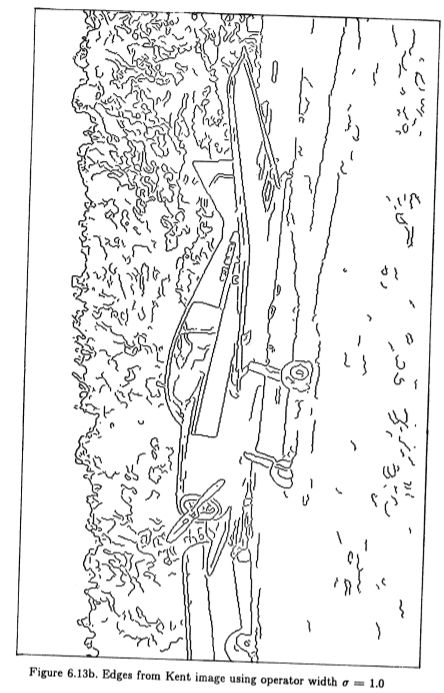
图6.13a：肯特图像
图6.13b：使用算子宽度 = 1.0的肯特图像边缘
图6.14a：威斯敏斯特图像
图6.14b：威斯敏斯特图像的边缘，操作员宽度 = 1.0
图6.15a：海洋图像
图6.15b：操作员宽度 = 1.0处的边
6.3 寻线器
在第4章中推导出了一个最佳的山脊算子。指出该算子向二维的扩展比边缘检测器更加困难，因为它缺乏自然属性（例如梯度），可以用于确定山脊的方向。脊检测器必须依靠更多的噪声量（大约是最大曲率的方向）来执行非最大抑制。由于方向和宽度的变化以及接合处的存在，印刷文本对于脊形检测器来说是一个困难的测试案例。图（6.16）给出了一些印刷文本上的脊线检测器输出。它使用高斯的二阶导数来近似在第（4.1）节中得出的最优算子。作为参考，图（6.17）给出了同一图像上的边缘检测器输出。脊线检测器的输出在主观上更清晰，但是在许多地方，轮廓部分是不正确的。
原则上，应该可以使用特征合成（或某些其他特征集成方法）将脊形检测器输出合并到阶梯边缘检测器中。到目前为止，这尚未完成，仍然是低视力计划的挑战。
图6.16a：（a）文字图像，（b）使用= 0.7的负脊检测器输出
图6.17：边缘检测器在文本图像上的输出，= 1.0
6.4 心理物理学
我们已经为有效边缘检测器上的一组特定标准提出了理由，并且我们声称这些标准对于各种应用都是通用的。从理论上讲，在这些应用中使用的任何边缘检测器都应使用相似的标准，以及与这些标准一致的算法。人类视觉系统为以后的过程提供有关视野的结构信息，并且人类擅长立体深度感知。有理由认为它应该在早期执行边缘检测。
从第3章给出的论点来看，建议使用各种操作符宽度和方向也是合理的。因此，当小型运营商具有足够的信噪比时，应优先考虑它们。为了检验这个假设，我们需要以某种方式产生一个图像，该图像在两个尺度上具有不同的细节，然后添加噪声以查看感知是否改变。这样的图像是Harmon和Julesa（1973）使用的Abraiam Lincoln的粗糙采样图片。粗采样的效果是在小范围内引入无关的细节。细节使图像难以感知，除非模糊。
图6.18：一张人脸的图像，其中有不同数量的加性高斯白噪声。
如果将噪声添加到图像中，则应观察到相同的效果，因为小运营商的信噪比将在大运营商之前变得无法忍受，因此在高噪声水平下应忽略较小的信道，而较大的信道仍然会包含连贯的信息。图（6.18）显示了一个众所周知的立体声类型（不是林肯）的粗略采样图像。连续的帧没有被模糊，但是包含越来越多的加性高斯白噪声。后面的帧更容易被感知为人脸。因此，我们有一种特殊的情况，即在这样的图像上添加非相干噪声会使其更容易察觉。
图6.19：具有正弦变化和加性高斯噪声的近似平行线的图像
第3章中分析的第二个结果是，定向性较高的算符比定向性较低的算符具有更好的信噪比。方向性强的操作员对边缘轮廓的方向的快速变化不太敏感，并且倾向于使快速变化的轮廓看起来更直。图（6.19）包含一系列平行线，这些平行线在其长度上局部弯曲，但整体上呈直线。线之间的间距很近，因此较大的通道宽度（也可能会主观地使轮廓变直）将具有较差的信噪比。 将噪点添加到此图像时，线条会明显拉直。
与本发明的检测器相反，这将表明一种方案，当它们具有足够的信噪比时，优先选择定向性较低的算子。 但是，如果我们对定向算子使用更复杂的适用性测试，则可以解决明显的不一致问题。在本算法中，由于等值线与直线的近似性较差，方向性运算符将不适用于图（6.19）中的任何一个帧。 如果边缘轮廓不是笔直或在拐角处断裂，则简单的标准偏差适用性度量就很差。 如果图像有噪点，也很差，但是在这种情况下，定向运算符同样适用。 如果在适用性度量标准中考虑了图像噪声，我们期望增加噪声会增强定向算子的适用性，与（6.19）一致。
7 相关工作
既然我们已经详细研究了使用变分技术的边缘检测器的设计，就其设计目标和实现这些目标的方法，我们可以将其与其他方案进行对比。为了考虑已经提出的各种边缘检测方案中的任何可观的部分，有必要对这些方案进行分类。实际上，大多数方案并不完全属于这些类别之一，而是保留了其中几个方面。我们将基于它们对以下目标的明显承诺来研究几个探测器
（i）根据近似真实图像表面的最适合表面，确定边缘的存在及其位置的估计。
（ii）为了最佳地估计图像中每个点上通常是一阶或二阶的一些导数，并在这些导数输出的局部特征处标记边缘，例如，二阶导数的零交叉或一阶导数的最大值。
（iii）频域技术，尝试通过滤波增强边缘。在这里，滤波器是使用频域技术设计的，通过假定背景的某些频率分布，可以最佳地将阶跃边缘与背景区分开。
所有比较都是理论上的，并且通常是定量的，因为对于早期视觉而言，算法的性能水平至关重要。 对于更广泛的调查，读者可以参考Davis（1975）。 为了进行实验比较，读者应该看Fram和Deutsch（1975），该书比较了应用于噪声阶跃边缘的几种算子，并包括了在相同合成图像上与人的表现的比较。 Abdou和Pratt（1979）根据品质因数比较了局部差分运算符和模板匹配运算符，该品质因数与本检测器中使用的性能标准非常相似。品质因数由Pratt（1978，p495）提出，由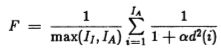
其中，II 和IA 是理想边缘点和实际边缘点的数量，d（i）是第 i 个像素与真实边缘的距离，而A是确定检测和定位之间权衡取舍的比例常数。
7.1 表面拟合
有许多基于某种图像表面建模的边缘检测器。这些方法通常包括根据一组基本函数对图像表面进行初始参数设置，然后根据参数a估计最合适的阶跃边缘的幅度和位置。这种方法的最早例子之一是Prewitt运算符（1970），它使用了二次函数的基函数集。另一个早期的例子是Hueckel（1971）的探测器。休克尔的方法将基函数与圆形支撑配合使用，并尝试将单个台阶边缘拟合到每个圆形区域。选择基函数以便给出圆形区域的近似傅立叶变换。但是，与大多数曲面拟合方案一样，基集并不完整（在52个像素的支持上只有8个基函数），并且实际上将边缘设置为原始曲面的平滑版本。提出了这样一种论据，即选择基函数完整空间的低频子集不会损害操作者检测和定位边缘的能力，但是没有给出证明。相反，有人认为应该忽略高频分量，因为它们将包含很多图像噪声。
这种方法的另一个示例是Haralick的工作。 在Haralick的1980年文章中，他提出了通过小的平面或“小平面”对图像进行拟合的方法，当两个表面的参数不一致时，在属于两个小平面的点上标记边缘。 每个表面在其邻域内的优度，并使用x平方统计量。再次，初始表面拟合包含一组不完全代表图像表面的参数，在这种情况下，一个正方形支撑上有3个参数，介于 实际上是4个像素和25个像素，这三个参数实际上是对x和y斜率以及支撑物上的平均值的估计。
在随后的使用更通用的表面拟合技术进行边缘检测的工作中，Haralick（1982）使用了具有较大运算符支持的高阶多项式基函数。 后一种方案在建模图像表面的二阶导数中沿图像梯度方向在零交叉处定位边缘。 它使用三次多项式（在x和y中）作为（通常）121个像素的平方支持的基函数。 有趣的是，基函数的这种选择产生了一个运算符，可以证明该运算符与本报告中描述的运算符非常相似。 但是，如果使用高阶或低阶多项式，性能将会变差。 现在我们证明这种相似性。
所使用的多项式是离散的Chebychev多项式，表示为Pi（r），为简单起见，我们将考虑一维问题。 表面拟合的目的是找到系数ai 以使总和
给出与实际采样图像表面 I（r）的最佳平方误差拟合。 那就是我们试图使...的价值最小化
我们通过将每个aj 的e2 的偏导数设置为零来实现。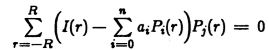
这导致了aj 中线性方程组的解，但是在多项式正交的情况下，该系统是对角线的，并且该解很简单
其中
然后，该方法估计此建模曲面的第一和第二部分导数。 例如，第一部分导数是
将公式（7.10）代入（7.11），我们得到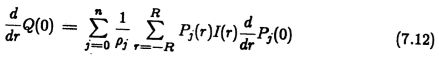
关于该方程式要注意的重要一点是，它在采样的图像强度中是线性的，因此可以将表面拟合操作后进行导数估算的过程表示为单个卷积。 我们从（7.12）找到了用于该卷积的等效滤波器。 由于该表达式具有r 上离散卷积的形式，通过去除r 和输入项 I（r）的和，可以得到等效滤波器的脉冲响应
第二方向导数的表达式的推导是相似的。 表面拟合方法的下一步是在第二方向导数的零交叉处标记边缘。 这些将对应于上面给出的一阶导数中的最大值。 这使我们处于能够直接将表面拟合方法与本报告中所述的变分方法进行比较的位置。 两种方法都使用一些线性算子有效地标记了图像卷积输出中最大值处的边缘。 我们可以使用为阶梯边缘定义的最佳标准来（解析地）评估曲面拟合算子的性能。
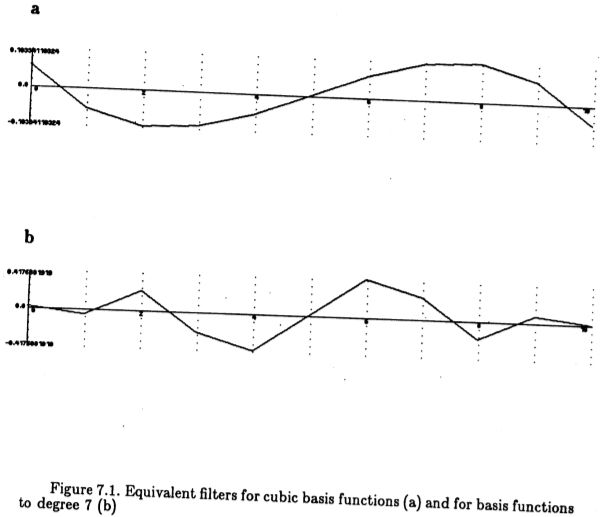
等效滤波器的形式直接取决于基函数Pi 的选择。切比切夫基多项式的三阶等效滤波器如图（7.1）所示。事实证明，三次基多项式的选择为该报告中得出的最优算子提供了最佳近似。敏锐的读者可能会注意到，表面拟合和坡度估计过程等同于与最近似于导数函数的函数（在基本函数所施加的约束范围内）进行卷积，即滤波器的脉冲响应为第一个三角函数的导数。参考（7.13）表明，随着基函数的阶数变大，滤波器 f（r）趋向于一个简单的局部梯度估计器，类似于3像素的Prewitt算子。图（7.1）的第二帧显示了n = 7的等效滤波器。
图7.1：用于三次基函数（a）和7级基数（b）的等效滤波器
因此，这种方法使三阶Chebychev多项式表现出最佳性能，而高阶多项式导致的算子近似于局部导数算子。这回答了Haralick在其文章中提出的关于多项式函数的最佳顺序的问题之一。提出了另一个问题的答案，即。也可以回答使用哪种形式的基本函数，因为他的绩效标准与我们的基本相同。请注意，这些标准用于实验评估表面拟合算子的性能，但在设计中并未明确显示。台阶边缘的最佳曲面拟合算子将使用一个单基函数，该函数是此处导出的高斯的一阶导数。使用此单基函数进行拟合和梯度估计等效于使用相同函数进行卷积。
因此，我们看到表面拟合方法的最终性能完全取决于基函数的选择。 但是，在Haralick（1980）或Hueckel（1970）中没有对它们各自功能的最优性进行分析。 表面拟合方法的其他倡导者对基础函数进行了更详细的分析。 例如，Hummel（1978）建议将Karhunen-Loeve主成分用于基本函数。
7.2 导数估计
由于理想的阶跃边缘是从一个强度值到另一个强度值的快速过渡，因此，检测边缘的合理方法似乎是估计图像强度表面的某种导数。一阶导数检测器已由Roberts（1965），Prewitt（1970），Rosenfeld和Thurston（1971），Macleod（1970）等提出。估计图像强度的二阶导数的算子也引起了人们的兴趣。 Modestino和Fries（1977）的运算符使用计算效率高的递归滤波算法来估计高斯平滑的拉普拉斯算子。 Herskovits和Binford（1970）使用一种侧向抑制的形式来降低其操作员对缓慢梯度的敏感性，然后进行一阶和二阶导数估计来定位边缘。近年来，对在零方向上沿梯度方向定位二元交点的算子产生了兴趣，即Havens和Strikwerda（1983），Tore和Poggio（1983），Yuille（1983）和Haralick（1982）。
我们应该注意到，第2章和第3章派生的运算符与上述两个运算符有非常强的相似性。特别是，我们一直在使用高斯的一阶导数来逼近第2章中推导的最优算子。它的最简单的二维扩展是使用高斯投影函数，该函数导致了一个二维算子，该算子与麦克劳德的。正如我们稍后将看到的，它至少在一个维度上与Marr-Hildreth算子非常相似。
在本报告中已经论证了最佳边缘检测函数应该是不对称的（请参阅第2.1节），因此可以将其视为一阶导数算子。但是，它并不是为了最佳估计梯度而设计的，而是用于检测台阶边缘的。这种区别是微妙的，但在这一点上应该强调。用于导数估计的论点是图像梯度在台阶边缘的中心达到最大值，因此可以通过找到梯度的最大值来检测边缘。但是，并不能因此认为梯度是检测和定位边缘的最佳方法。 Marr和Hildreth（1980）建议使用高斯算子的拉普拉斯算子的输出斜率。再次观察到，该数量与边缘强度成正比。
我们确实应该尝试估计潜在边缘的“边缘性”，但是这种度量只能通过变分方程（如方程（2.12））隐式定义，趋势是使用后验度量，例如梯度边缘附近出现高梯度这一事实并不意味着高梯度的所有点都与边缘相对应。
由于在一维中二阶导数算子（Marr和Hildreth）的零交叉与一阶导数算子的最大值基本相同（暂时忽略阈值问题），并且都采用高斯预卷积，因此我们期望相似 两家运营商的业绩。 在两个方面，扩展是不同的，并且性能明显不同。 现在我们证明，高斯的二维拉普拉斯算子比第3章中描述的方向算子给出的定位更差。让高斯的二维拉普拉斯算子由等式描述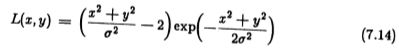
现在通过第3章的方法，过零位置的标准偏差是边缘中心处的过零斜率与操作员输出中均方根噪声的商。 令输入为在y方向上幅度为A的阶跃，即输入S（x，y）的方程为
那么过零的斜率是
均方根输出噪声为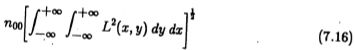
用（7.15）除以（7.16）再用（7.14）代替，我们发现高斯拉普拉斯算子的局部化
恰好
我们将其与与边缘对齐的定向算子的定位进行比较。 让该算子的点扩展函数由以下方程式描述
同样，我们找到（7.15）和（7.16）的商并用（7.17）替代，我们获得了该算符的本地化
因此，平均而言，我们期望高斯的拉普拉斯算子的位置误差比相同的方向算子的位置误差大60％。
已经提出，可以从零交叉的斜率（垂直于边缘方向）估计零交叉的强度。 我们还应该将此度量的信噪比与一阶导数的信噪比进行比较。 高斯的拉普拉斯算子的零交叉的斜率再次由公式（7.15）给出，而该值的噪声可以从积分中找到
这给出了高斯的拉普拉斯算子的信噪比
L，由方程（7.15）和（7.18）的商
最后，我们将该值与二维方向导数算子的信噪比进行比较
原来的值为
这种比较表明，有向一阶导数算子对高斯的拉普拉斯算子（带斜率估计）相对于信噪比略好于2，对局部较好约1.6倍。根据综合准则
，我们发现
以上结果表明，过零的斜率对于边缘强度的估计非常差。尽管边缘幅度估计器还有其他可能的选择，但我们还发现，与方向算子相比，高斯的拉普拉斯算子仍然局限在局部位置。这样做的直观原因是，二维拉普拉斯算子可以分解为两个（任意）正交方向上的二阶导数之和。如果选择其中之一垂直于边缘方向，则很明显，这种贡献恰好是定向算子的贡献。但是，第二个分量将平行于边缘方向，对定位没有任何帮助，但会增加噪声量。
7.3 频域方法
在这一（相当小的）类别中，我们找到了一种方法的特定示例，该方法使用的标准与我们的标准非常相似，并且使用了频域推导。 我们可能期望这种表述会导致与我们非常相似的运营商。 实际上并没有，但这是由于对可能的解决方案施加了相当不幸的限制。 当消除限制后，我们再次获得近似高斯一阶导数的函数。
方法是Shanmugam等人（1979）的方法，他提出了使用近似于高斯拉普拉斯算子的二维线性算子。 他们的最优标准是，当函数与阶跃边缘卷积时，该函数将限制在固定间隔内的总输出能量比例最大化。 此外，该功能必须严格限制带宽。这两个标准大致反映了本设计的标准。间隔中总输出能量比例的最大化将限制范围，在该范围内可能会出现最大阶跃响应。频带限制极大地提高了输出信噪比，因为高斯噪声的频谱是平坦的，而阶跃边缘的频谱却随频率的倒数而变化，即，边缘中的大部分能量都集中在低频。
不幸的是，Shanmugam等人的方法有两个步骤，本作者发现很难证明这两个步骤。首先是他们没有尝试标记边缘点，而是输出了阈值滤波值。实际上，它们的滤波器在对理想阶跃的响应中给出了两个峰值，但它们位于阶跃中心的任一侧，并且中心的响应实际上为零。这在Marr和Hildreth（1980）的工作中得到了一定程度的纠正，他们使用了同一滤波器的零交叉，因为这些特征出现在台阶边缘的中心。
第二个问题是，他们先验地认为所寻找的操作员可以通过绕对称轴旋转而将操作数扩展到二维。这立即将它们限制在对称算符上，即使在完成设计的一个维度上也是如此。正如我们在第3章中看到的那样，此限制是不必要的，实际上会降低性能。实际上，如果取消了限制，则相同的分析会导致运算符逼近当前设计中使用的高斯一阶导数。我们现在不假设对称性地重复它们的设计。
我们再次执行优化，以找到将一个准则极端化而另一个准则保持不变的函数。 在这种情况下，响应Q的带宽将是固定的，而间隔 [-I / 2，+ I / 2] 中总输出能量的分数将最大化，即，如果输出响应为 g（x），且 间隔中的能量为
，我们最大化
我们可以利用以下事实：存在一组函数
扁球面波函数，它们受到频带限制，在间隔[-I / 2，+ I / 2]上正交，并且在（-oo ，+ oo）即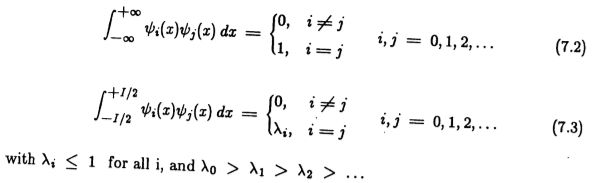
扁长球面函数在带限函数的空间中是完整的，因此任何带限滤波器的输出都可以表示为
其中常数c是带宽和间隔大小的函数
当使用（7.2）和（7.3）的结果将g（x）的展开代入（7.1）时，的值变为
都是正数，并且
，所以B的边界是
当n >0时，当 an = 0时达到上限，因此最佳输出为
由于这是滤波器的期望阶跃响应，因此我们可以通过微分获得脉冲响应f（x）。
Slepian（1965）对函数
的近似可用于找到 f（x）的闭式表达式。
其中Hn（x）是n级的Hermite多项式。 对于x 
可以由高斯近似，并且最佳空间函数f（x）将像以前一样是高斯的一阶导数
在他们的原始文章中，当Shanmugam等人（1979）假设函数f（x）应该是对称的时，它们被限制在忽略的奇长球状函数中，而实际上提供了最佳性能。 
i（c）可以用作性能指标，因为它们测量指定区域中对应的
总能量的分数。对于较小的c值，入0 的值可能明显高于入1 的值。 c的小值表示空间和频率范围的乘积最小。例如，在c = 0.5时，入0 的值约为0.3，而 入1 的值为0.0086（请参见Slepian 1960）。
本章的目的是将本边缘检测器与其他几种众所周知的方案结合起来。我们已经看到，分析形式与这些方案中的几种有很强的相似性，特别是与Marr和Hildreth，Macleod，Haralick和Shanmugam等人的探测器。还有一些重要的区别，例如，我们尚未考虑使用多个运算符或高度定向的蒙版。
Rosenfeld（1971）使用了几个不同的盒子，并通过优先选择最大的算子来形成复合边缘图，该最大的算子没有比下一个较小的算子低得多的响应。 Marr（1976）既对高度定向的运算符进行了争论，也对多重尺度进行了争论，但由于在实现它们方面存在明显的困难，因此在后来的文章（1980）中拒绝了第一个要求。 本设计产生的边缘图在原理上与1976年版本的原始草图非常相似，后者纯粹是出于计算方面的考虑。
8. 进一步工作的结论和建议
我们在开始这份报告时首先对一组边缘检测目标进行了精确定义，然后继续推导最能达到这些目标的操作员。这些目标是在关于最佳边缘算子形式的最小假设下精心选择的。施加的约束是我们将在线性不变移位算子的输出中的最大值处标记边缘。通过将标准表示为基于边缘检测算子的脉冲响应的函数，我们能够在较大的解决方案空间上进行优化，而无需对解决方案的形式施加约束。
在第2章中，将这种技术与高斯白噪声中阶跃边缘的初始模型一起使用时，我们发现阶跃边缘的同时检测和定位存在根本限制。这导致边缘检测器的定位和检测能力之间的自然不确定性关系。这种关系反过来导致对解决方案的强大约束，即存在一类最优算子，所有这些最优算子都可以通过空间缩放从单个算子获得。通过改变该运算符的宽度，可以改变信噪比与本地化之间的权衡，同时确保对于数量之一的任何值，另一个将最大化。
然后发现，最初指定的目标没有得到很好的定义，或者分析标准并未阐明我们对边缘检测器的所有期望。 通过添加与多个响应相关的明确标准，我们能够获得一个满足我们所有直观设计目标的操作员。 多重响应约束确实增加了解决方案形式的复杂性，实际上，不可能以完全封闭的形式实现解决方案。 但是，分析能够将解约束到一个有限的（低）维参数空间，可以在该空间上获得数值解。 算子的冲激响应是阻尼指数余弦的总和，可以用高斯的一阶导数来近似。
然后，我们将上述运算符扩展到二维，并以此为基础遵循了第2章为一维公式建立的框架。检测和定位的基本标准是在扩展到二维方面令人担忧的问题。已经发现，由于上述折衷，需要多个操作员宽度来处理图像中的不同信噪比。我们还发现，定向算子比非定向算子具有明显的优势，并且定向算子越多，其潜在性能就越好。通过使用拟合优度来确定是否可以使用每个定向算子，来解决与高度定向算子相关的传统问题。然后，我们面临着将所有这些功能描述组合成一个连贯的整体的巨大问题。我们再次使用相同的设计目标集来指导启发式方法，以选择合适的运算符。提出了特征综合，作为组合对相同特征的响应在空间上不一定一致的算子的输出的一种方法。
首选启发式方法是优先选择最小宽度的运营商，前提是他们具有足够的信噪比。对于给定的全局信噪比，这可以提供最大的分辨率和定位。由于缺少不同运算符输出的空间一致性，因此很难组合不同运算符宽度。对于操作员集成，必须使用特征综合（在第6章中给出了示例）。
第二种启发式方法是在具有足够的图像拟合质量时偏向于高度定向的运算符。不同操作员方向的集成相对简单，仅需要稍微复杂一些的非最大抑制形式。在第6章中给出了该技术的示例。目前尚不清楚应使用哪种拟合优度，并且尽管提出了一种算法，该算法性能良好，但没有证明它的适时性。实际上，有一些证据（第6.4节）表明，在其他方面证明与此处所述检测器相似的人类视觉系统使用了不同（或更复杂）的决策程序。
为了使具有最佳算子的图像卷积更加有效，使用了高斯近似的一阶导数。这使我们能够使用第3.2节中介绍的任何有效算法来加快处理速度。结果发现，使用任意遮罩进行卷积大约有一个“内部”时间（在正方形遮罩的宽度内）算法，因此即使不进行近似也可以进行有效的卷积。在硬件中实现此方案。
在第4章中，我们将用于高斯白噪声的阶跃边缘的方法概括为任意特征和非白色但平稳的随机噪声。除了标准的一般形式外，还介绍了一种用于解决方案的快速数值方法。然后，使用该技术为山脊和屋顶特征找到最佳算子。脊检测器被扩展到两个维度，并且由于缺少关于脊方向的可靠信息，发现这比边缘操作者要困难得多。脊检测器输出的示例出现在第（6.3）节中，并与同一图像上的边缘检测器进行了比较。
最后，在第6章和第7章中，对此处导出的边缘检测器，Marr-Hildreth（1980）运算符和Boxes差分运算符进行了比较。既有分析比较，也有实验比较。还将它与其他两个边缘算子Haralick（1982）和Shanmugam等人（1979）进行了比较，发现它们在一个维度上都与所有这些相似，第6章还包括边缘检测器输出的几个示例。最后，我们在6.5节中看到了一些感官效果，这些感官效果似乎表明人类视觉系统使用了类似的特征组合方案。
（i）集成方案不应遗漏特征，如果单个特征被检测器之一标记，则应在积分器输出中对其进行标记。（i）集成方案不应遗漏特征，如果单个特征被检测器之一标记，则应在积分器输出中标记该特征；此外，如果两个特征检测器在同一点上的响应方式不是 如果图像中只有一个ingle功能，则积分器应在输出上标记这两个功能。
（ii）集成方案应产生具有最小冗余的输出。 根据标准（i）表现良好的明显方案是简单标记任何特征检测器看到的所有内容。 在这种情况下，不会发生特征信息的整合，例如，如果已经针对某个特征识别出一条脊，则无需将其标记为两个平行的紧密间隔的边缘。 可以将特征积分器视为所有特征检测器输出上的滤波器，以去除冗余信息。
以上两个标准均要求使用非本地方案，也就是说，它必须考虑附近特征检测器的输出，而不仅仅是单个点的输出。特征合成是一种非局部方案，Haralick（1983）的“地形原始草图”中使用的表面拟合方法也是如此。值得根据上述标准比较这两种方案。使用优化方案找到最佳特征积分器的困难在于，将需要更为复杂的图像模型。至少它需要包括所有为单个检测器设计的特征，以及这些特征的所有可能组合。
边缘检测器的另一可能的扩展将是3维或更多维。我们已经在第3章中看到，最优算子可以简单地扩展到n维。该运算符定位强度发生不连续的n-1个表面（边缘轮廓的n维扩展）。由于要均匀覆盖一个n球需要大量的方向，因此在此域中使用高方向性运算符会更加困难。出于相同的原因，非最大抑制也更加复杂。
特别地，可以将移动边缘的检测视为三维边缘检测问题，其中第三维是时间轴。该三维空间中的边缘对应于二维图像中的边缘或辐照度快速变化的点。在三个空间中边缘的方向可用于确定二维边缘的速度。时空边缘滤波器必须具有因果关系，即必须仅取决于过去和现在的强度值。使用时域较宽的滤波器会在速度估计中引入延迟。因此，时域滤波器的设计是一个单独的优化问题，它需要因果关系和最小时间延迟的附加约束。
本报告中描述的技术的一种最终概括将是放宽对操作员的线性限制。移位不变性显然是边缘检测算子的理想属性，但尚不清楚最优算子必须是线性的。实际上，此报告中得出的复合运算符是非线性的，因为它涉及应用于多个运算符输出的非局部谓词（来自特征综合方案）。理想情况下，应该放宽此约束，或者应该证明线性算子的性能与非线性算子一样好。在这里限制线性运算符是必要的，因为以一种允许应用变分方法的形式对非线性移位不变算符进行参数设置非常复杂。此限制是否会影响性能，以及不受约束的非线性算子能否做得更好，还有待观察。
附录I.微分中使用的定积分
这些积分在第2章中已提及，但由于篇幅过长而未包含在其中。 要评估（2.12），需要3个积分，而对于（2.24），则需要一个额外的积分。 在这4个积分中，有3个可以用相同的参数形式编写，因为它们都包含该形式的函数的平方的积分
现在我们定义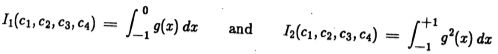
而且我们发现性能标准中的所有积分都可以用I1和I2来表示
其中
定积分I1 的从 
，w和c1到c4以及单位间隔（W = 1）的闭合形式为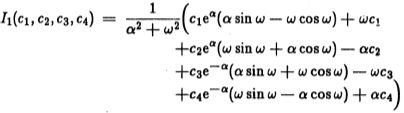
同样，单位间隔内I2 的闭合形式为
参考文献
Aldou.I.E. and Pratt W.K."Qusntitative Design and Eraluation of Eahancement/Thresholding Edge Detectors," IEEE Proc. 67,No. 6(1979), 753-763.
Binford T.0."Inferring Surfaces from Images," Artijicial Inteligence 17(1981), 205-244
Biagham C, Godfrey MD, Takey J.W." Modern Techniques of Power Spectrum Estimation,” IEEE Trans. A.E.AU-15, No 2(1967), 56-66.
Brady J.Mand Aswda H. "Smoothed Local Symmetries and their Implementation," To appear (1983).
Courant R. and Hilbert D. Mcthods of Mathematical Physics, vol.1,Wiley Interscience, New York, 1953.
Davis L. S. "A Survey of Edge Detection Techniques," Computer Graphics and Image Processing 4(1975), 248-270.
Fram J. R.and Deutach E. S. "On the Quantitative Eraluation of Edge Detection Schemes and Their Comparison with Human Performance," IEEE Trans. Computers C-24, No.6(1975), 616-628.
Grimson W. E. L. From Images to Surfaces, MrT Press, Cambridge, Ma., 1981.
Hamming R. W. Digital Filters, Prentice Hall, New Jersey, 1983.
Haralick R. M. "Edge and Region analysis for Digital Image Data," Computer Graphics and Image Processing 12(1980), 60-73.
Haralick R. M. "Zero-crossing of Second Directional Derivative Edge Operator," S. P. I. E. Proceedings on Robot Vision, Arlington Virginia,1982.
Haralick R. M, Watson L. T.and Lafey T. L. "The Topographic Primal Sketch," Robotics Research To appear (1983).
Havens W. S.and Strikwerda J. C. "An Improved Operator for Edge Detection," To appear(1983).
Herskovits A.and Binford T. “On Boundary Detection, "M. I. T. Artificial Intelligence Laboratory, Cambridge Mass., Al Memo 183, 1970.
Hildreth E.C. "Implementation of a Theory of Edge Detection, "M. I. T. Artificial Intelligence Laboratory, Cambridge Mass., Al-TR-579, 1980.
Hildreth E. C. "The Measurement of Visual Motion, "Ph. D. Thesis, Dept.of Electrical Engineering and Computer Science, MIT, Cambridge, Ma, 1983.
Horn B. K. P. "The Binford-Horn Line-Finder," M. I. T. Artificial Intelligence Laboratory, Cambridge Mass., Al Memo 285, 1971.
Horn B. K. P. "Obtaining Shape from Shading Information," The Psychology of Computer Vision P. H. Winston, ed, McGraw Hill, New York, pp 115-155, 1975.
Hueckel M. H. "An Operator Which Locates Edges in Digitized Pictures,” JACM 18, No.1(1971)，113-125.
Hummel R.A. “Edge Detection Using Basis Functions," Computer Graphics and Image Processing 9(1979), 40-55.
Jacobus C. J. and Chien R. T. "Two New Edge Detectors,” IEEE Trans. P. A. M. I. PAMT-3, No.5(1981), 581-592.
Liskov B., Atkinson R, Bloom T, Moss E., Schafert C, Scheifler B., and Snyder A." CLU Reference Manual,” MIT Laboratory for Computer Science, TR-225, 1979.
Luenberger D. G. Introduction to Linear and Non-Linear Programming, Addison-Wesley, Reading,Ma.,1973.
Macleod I. D. G. "On Finding Structure in Pictures,” Picture Language Machines S. Kaneff ed. Academic Press, New York, pp 231,1970.
Marr D.C." Early Processing of Visual Information," Phil.Trans. R. Soc.Lond. B275(1976), 483-524.
Marr D. C.and Hildreth E. “"Theory of Edge Detection," Proc.R. Soc. Lond. B 207(1980）, 187-217.
Marr D. C. and Poggle T. "A Theory of Human Stereo Vision," Proc. R. Soc. Lond. B 204 (1979), 301-328.
Modestino J. W. and Fries R. W. "Edge Detection in Noisy Images Using Recursive Digital Filtering.” Computer Graphics and Image Processimg 6 (1977), 409-433.
Moon D,Stallman R. M, Weimch D." Lisp Machine Manual," MIT Cambridge, Ma,1983.
Peatland A. P. "Local Shape from Shading." Ph. D. Thesis, Dept. of Paychology, MIT,Cambridge, Ma, 1982.
Pratt W. K. Digital Image Processing, Wiley Interscience, New York, 1978.
Prewitt J. M. S. "Object Enhancement and Extraction," Picture Processing and Paychopictorics B. Lipkin & A. Rosenfeld Eds, Academic Press, New York, pp75-149, 1970.
Rice S.o. "Mathematical Analysis of Random Noise," Bell Sys. Tech. J. 24 （1945）, 46-156.
Roberts L. G. "Machine Perception of 3-Dimensional Solids," Optical and Electro-Optical Information Processing J.Tippett, D. Berkowitz, L. Clzpp, C. Koester, A. Vanderbergh Eds, M. 1. T. Press, Cambridge, pp 159-197, 1965.
Rosenfeld A. and Thurston M. "Edge and Curve Detection for Visual Scene Analysis,” IEEE Trans. Computers C-20, No. 5(1971), 562-569.
Schonhage A., and Strassca V. "Schnelle Multiplikation grosser Zahlen," Computing 7（1971）, 281-292.
Shanmugam K. S, Dickey F M.& Green J. A. "An Optimal Frequency Domain Filter for Edge Detection in Digital Pictures," IEEE Trans. P. A. M. I PAM-1, No.1(1979), 37-49.
Slepian D. "Some Asymptotic Expansions for Prolate Spheroidal Wave Functions," J. Math. Phys. MIT 44(1965), 99
Stevens K. A. "Surface Perception from Local Analysis of Texture and Contour," M. I. T. Artificial Intelligence Laboratory, Cambridge Mass, Al-TR-512,1980.
Torre V. and Poggio T. "A Directional Second Derivative Zero-crossing Operator," To appear, 1983.
Uman S. The Interpretation of Visual Motion, MIT Press, Cambridge, Ma, 1979.
Wiener N. Extrapolation, Interpolation and Smoothing of Stationary Time Series, MIT Press, Cambridge, Ma, s., 1949.
Witkin A. P. "Shape from Contour," M. I. T.Artificial Intelligence Laboratory, Cambridge Mas，AI-TR-589, 1980.
Yuile A. "Zero-Crossings on Lines of Curvature," M. I. T. Artificial Intelligence Laboratory, Cambridge Mass., To appear, 1983.