机器人学回炉重造（2-1）：雅可比矩阵的定义

写在前面

我是把讲义以及笔记上的内容原封不动的搬过来，做个记录保存，不喜勿看。实现代码在最后面。

前文提到机器人的正运动学，实现代码是直接使用matlab里的机器人工具箱。下面我用matlab自写一个求（改进D-H）正运动学齐次变换矩阵的代码：

function T0 = myforward(theta)
% Modified D-H参数
th(1) = theta(1); d(1) = 0; a(1) = 0; alp(1) = 0;
th(2) = theta(2); d(2) = 0; a(2) = 0.320; alp(2) = pi/2;
th(3) = theta(3); d(3) = 0; a(3) = 0.975; alp(3) = 0;
th(4) = theta(4); d(4) = 0.887; a(4) = 0.2; alp(4) = pi/2;
th(5) = theta(5); d(5) = 0; a(5) = 0; alp(5) = -pi/2;
th(6) = theta(6); d(6) = 0; a(6) = 0; alp(6) = pi/2;
T0 = eye(4);
for i = 1:6
    Ti(:, :) = [cos(th(i))             -sin(th(i))            0            a(i);
                sin(th(i))*cos(alp(i)) cos(th(i))*cos(alp(i)) -sin(alp(i)) -sin(alp(i))*d(i);
                sin(th(i))*sin(alp(i)) cos(th(i))*sin(alp(i)) cos(alp(i))  cos(alp(i))*d(i);
                0                      0                      0            1];
%     T(i*4-3:i*4, 1:4) = Ti(:, :);
    T0 = T0 * Ti;
end
end

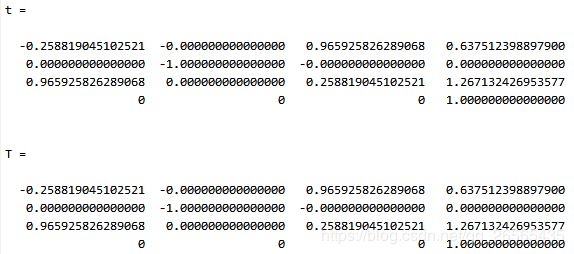
还是前面ABB的例子和初始位姿，可以看出上面代码能够得到与工具箱一样的结果

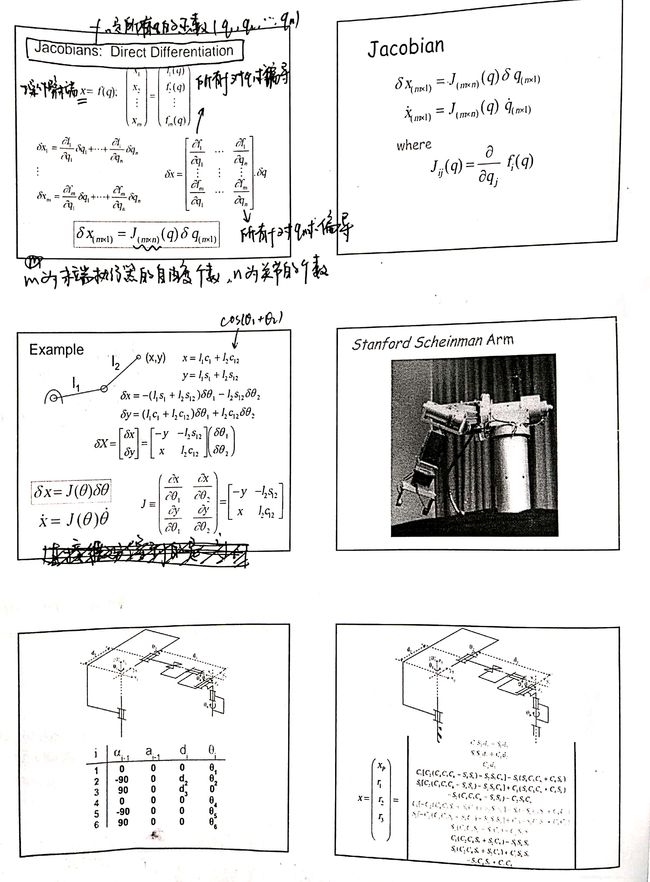
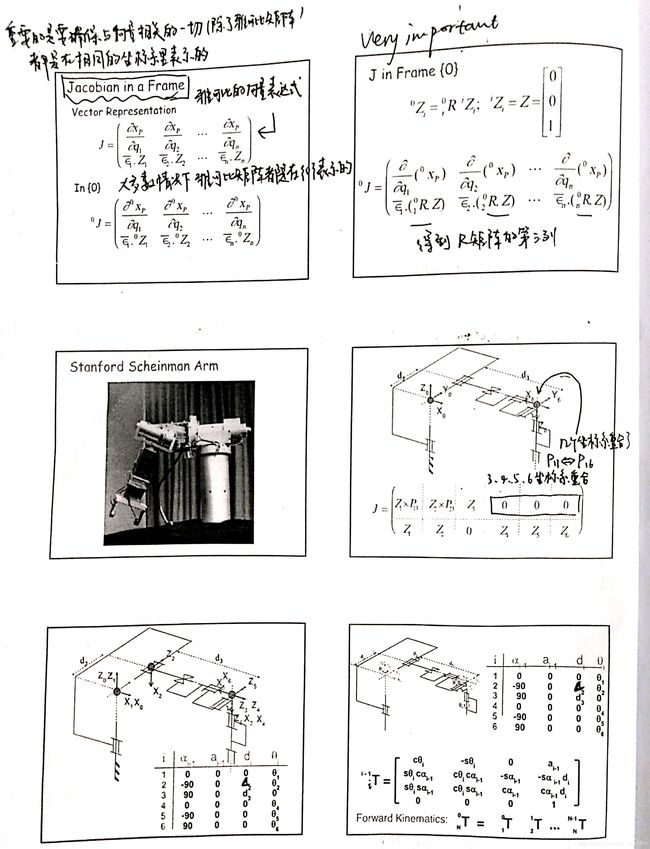
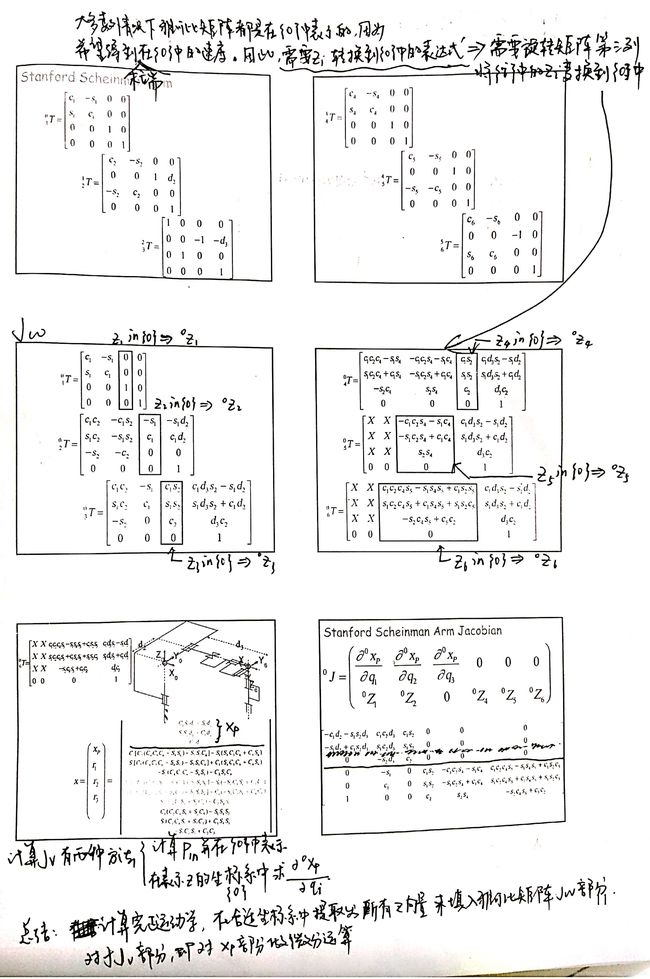
雅可比矩阵

Matlab实现

同样以前文ABB机械臂为例，初始位姿为theta = [0, 120, -15, 0, 0, 0]*pi/180。工具箱的实现代码很简单

j = robot.jacob0(theta)

自写代码为：

%% 求齐次变换矩阵
function T = Trans(alpha, a, d, theta)
T= [cos(theta)             -sin(theta)            0            a;
    sin(theta)*cos(alpha)  cos(theta)*cos(alpha)  -sin(alpha)  -sin(alpha)*d;
    sin(theta)*sin(alpha)  cos(theta)*sin(alpha)  cos(alpha)   cos(alpha)*d;
    0                      0                      0            1];
end

%% 计算雅可比矩阵
function J = jisuan(angle)
% Modified D-H参数
th(1) = angle(1); d(1) = 0; a(1) = 0; alp(1) = 0;
th(2) = angle(2); d(2) = 0; a(2) = 0.320; alp(2) = pi/2;
th(3) = angle(3); d(3) = 0; a(3) = 0.975; alp(3) = 0;
th(4) = angle(4); d(4) = 0.887; a(4) = 0.2; alp(4) = pi/2;
th(5) = angle(5); d(5) = 0; a(5) = 0; alp(5) = -pi/2;
th(6) = angle(6); d(6) = 0; a(6) = 0; alp(6) = pi/2;
% 各齐次矩阵function T = Trans(alpha, a, d, theta)
T01 = Trans(alp(1), a(1), d(1), th(1));
T12 = Trans(alp(2), a(2), d(2), th(2));
T23 = Trans(alp(3), a(3), d(3), th(3));
T34 = Trans(alp(4), a(4), d(4), th(4));
T45 = Trans(alp(5), a(5), d(5), th(5));
T56 = Trans(alp(6), a(6), d(6), th(6)); 
T02 = T01 * T12;
T03 = T02 * T23;
T04 = T03 * T34;
T05 = T04 * T45;
T06 = T05 * T56;
% J由JV和JW组成，前三行六列为JV，后三行六列为JW
for i = 1:6
    for j = 1:3
        JV(j, i) = diff(T06(j, 4), th(i));
    end
end
JW = [T01(1:3, 3), T02(1:3, 3), T03(1:3, 3), T04(1:3, 3), T05(1:3, 3), T06(1:3, 3)];
% 合并
J = [JV; JW];
end

%% 替换变量并代值计算
function J = myjacob(theta)

syms th1 th2 th3 th4 th5 th6;
angle = [th1, th2, th3, th4, th5, th6];

JT = jisuan(angle);
% 替换变量
JT1 = subs(JT, th1, theta(1));
JT2 = subs(JT1, th2, theta(2));
JT3 = subs(JT2, th3, theta(3));
JT4 = subs(JT3, th4, theta(4));
JT5 = subs(JT4, th5, theta(5));
J = subs(JT5, th6, theta(6));

digits(4)
J = vpa(J,8);

end

检验结果：

j = robot.jacob0(theta)
J = myjacob(theta)

1.theta = [0, 120, -15, 0, 0, 0]*pi/180;

2.theta = [90, 120, -15, 0, 20, 0]*pi/180;

3.theta = [90, 45, -15, 36, 20, 175]*pi/180;

参考

Introduction to Robotics