编译原理FIRST集和FOLLOW集的求法以及构建LL(1)分析表

FIRST集的求法

FIRST集是一个文法符号串所可能推导出的符号串的第一个终结符的集合
对于文法G的任一符号串$\alpha$ = $x_1{x}_2\dots x_n$

1. 置 FIRST($\alpha$) = $\varphi$
2. 将 FIRST($x_1$) 中一切非 $ϵ$ 符号加进 FIRST($\alpha$)
3. 若$ϵ\in$ FIRST($x_1$), 将 FIRST($x_2$) 中一切非 $ϵ$ 符号加进FIRST($\alpha$); 若 $ϵ\in$ FIRST($x_1$) 和 FIRST($x_2$), 将 FIRST($x_3$) 中一切非 $ϵ$ 符号加进 FIRST($\alpha$) 中, 依此类推.
4. 对于一切 1 $⩽$ i $⩽$ n, $ϵ\in$ FIRST($x_i$), 则将 $ϵ$ 符号加入 FIRST($\alpha$).

note:
FIRST集从产生式左侧推导，例如求A的FIRST集，要先从产生式左侧找到A，然后根据产生式右侧的信息求出A的FIRST集

例如：
S $\to$ BS${}^{‘}$
S${}^{‘}\to$ aB | $ϵ$
B $\to$ DB${}^{‘}$
B${}^{‘}\to$ b | $ϵ$
D $\to$ d | $ϵ$

FIRST(S) = {d, b, a, $ϵ$}
FIRST(S${}^{‘}$) = {a, $ϵ$}
FIRST(B) = {d, b, $ϵ$}
FIRST(B${}^{‘}$) = {b, $ϵ$}
FIRST(D) = {d, $ϵ$}

解释：
第一个求S的FIRST集，先从产生式的左侧找到S, (S$\to$ BS${}^{‘}$), 然后根据该产生式右侧的信息(BS${}^{‘}$) 和求FIRST集的第二条规则求FIRST(B), 从产生式的左侧找到B, (B$\to$ DB${}^{‘}$), 然后根据该产生式右侧的信息(DB${}^{‘}$) 和求FIRST集的第二条规则求FIRST(D), 从产生式的左侧找到D, (D$\to$ d | $ϵ$), 然后根据该产生式右侧的信息(d | $ϵ$) 和求FIRST集的第二条规则, 将终结符d加入FIRST(S).
$$FIRST(S)=\{d\}$$
又根据第三条规则，因为D$\to ϵ$, 所以将FIRST(B${}^{‘}$) 加入到FIRST(S)中，从产生式的左侧找到B${}^{‘}$, (B${}^{‘}\to$ b | $ϵ$), 然后根据该产生式右侧的信息(b | $ϵ$) 和求FIRST集的第二条规则, 将终结符b加入FIRST(S).
$$FIRST(S)=\{d,b\}$$
又根据第三条规则，因为B${}^{‘}\to ϵ$, 所以将FIRST(S${}^{‘}$) 加入到FIRST(S)中，从产生式的左侧找到S${}^{‘}$, (S${}^{‘}\to$ aB | $ϵ$), 然后根据该产生式右侧的信息(aB | $ϵ$) 和求FIRST集的第二条规则, 将终结符a加入FIRST(S).
$$FIRST(S)=\{d,b,a\}$$
又根据第四条规则，因为$ϵ\in$ FIRST(D) , $ϵ\in$ FIRST(B${}^{‘}$), 所以 $ϵ\in$ FIRST(B), 又因为$ϵ\in$ FIRST(S${}^{‘}$), 所以 $ϵ\in$ FIRST(S). 最终结果如下:
$$FIRST(S)=\{d,b,a,ϵ\}$$

第二个求S${}^{‘}$的FIRST集, 先从产生式左侧找到S${}^{‘}$, (S${}^{‘}\to$ aB | $ϵ$), 然后根据产生式右侧的信息(aB | $ϵ$), S既能推导出aB又能推导出$ϵ$, 所以根据规则二和规则四得出:
$$FIRST(S^{‘})=\{a,ϵ\}$$

第三个求B的FIRST集, 产生式的左侧找到B, (B$\to$ DB${}^{‘}$), 然后根据该产生式右侧的信息(DB${}^{‘}$) 和求FIRST集的第二条规则求FIRST(D), 从产生式的左侧找到D, (D$\to$ d | $ϵ$), 然后根据该产生式右侧的信息(d | $ϵ$) 和求FIRST集的第二条规则, 将终结符d加入FIRST(B).
$$FIRST(B)=\{d\}$$
又根据第三条规则，因为D$\to ϵ$, 所以将FIRST(B${}^{‘}$) 加入到FIRST(B)中，从产生式的左侧找到B${}^{‘}$, (B${}^{‘}\to$ b | $ϵ$), 然后根据该产生式右侧的信息(b | $ϵ$) 和求FIRST集的第二条规则, 将终结符b加入FIRST(B).
$$FIRST(B)=\{d,b\}$$
又根据第四条规则，因为$ϵ\in$ FIRST(D) , $ϵ\in$ FIRST(B${}^{‘}$), 所以 $ϵ\in$ FIRST(B), 最终结果如下:
$$FIRST(B)=\{d,b,ϵ\}$$

求第四个B${}^{‘}$的FIRST集和第五个求D的FIRST集同求第二个求S${}^{‘}$的FIRST集，结果为:
$$\begin{gathered} FIRST(B^{‘})=\{b,ϵ\} \\ FIRST(D)=\{d,ϵ\} \end{gathered}$$

FOLLOW集的计算

FOLLOW集是文法符号后面可能跟随的终结符的集合(不包括空串)

1. 对于文法的开始符号S，置 # 于 FOLLOW(S)中.
2. 若 A $\to$ aB$\beta$ 是一个产生式， 则把 FIRST($\beta$) \ |$ϵ$| 加至 FOLLOW(B) 中.
3. 若 A $\to$ aB 是一个产生式，或 A $\to$ aB$\beta$ 是一个产生式而 $\beta \Rightarrow ϵ$ (即 $ϵ\in$) FIRST(B), 则把 FOLLOW(A) 加至 FOLLOW(B) 中.

note:

1. FOLLOW集中没有 $ϵ$
2. FOLLOW集从产生式右侧推导，例如求A的FOLLOW集时，要从产生式右侧找到A，然后根据A右侧符号信息，求出A的FOLLOW集

例如：
S $\to$ BS${}^{‘}$
S${}^{‘}\to$ aB | $ϵ$
B $\to$ DB${}^{‘}$
B${}^{‘}\to$ b | $ϵ$
D $\to$ d | $ϵ$

FOLLOW(S) = {#}
FOLLOW(S${}^{‘}$) = {#}
FOLLOW(B) = FIRST(S${}^{‘}$) \ |$ϵ$| $\cup$ FOLLOW(S${}^{‘}$) $\cup$ FOLLOW(S) = {a, #}
FOLLOW(B${}^{‘}$) = FOLLOW(B) = {a, #}
FOLLOW(D) = FIRST(B${}^{‘}$) \ |$ϵ$| $\cup$ FOLLOW(B) = {b, a, #}

解释：
第一个求S的FOLLOW集, 因为S是开始符号，所以将#加入到FOLLOW(S)中，从产生式右侧找S，没有找到，所以最终结果:
$$FOLLOW(S)=\{\#\}$$
第二个求S${}^{‘}$的FOLLOW集, 从产生式右侧找S${}^{‘}$, (S $\to$ BS${}^{‘}$), 根据右侧符号信息和求FOLLOW集的第三条规则，将 FOLLOW(S) 加入到 FOLLOW(S${}^{‘}$) 中，最终结果:
$$FOLLOW(S^{‘})=\{\#\}$$
第三个求B的FOLLOW集，从产生式右侧找到B，(S $\to$ BS${}^{‘}$ 、S${}^{‘}\to$ aB | $ϵ$), 根据 S $\to$ BS${}^{‘}$ 和第二条规则，得:
$$FOLLOW(B)=FIRST(S^{‘})\setminus |ϵ|=\{a\}$$
根据S${}^{‘}\to$ aB 和第三条规则，得:
$$FOLLOW(B)=FOLLOW(S^{‘})=\{a,\#\}$$
又因为S${}^{‘}\to ϵ$, 根据S $\to$ BS${}^{‘}$ 和第三条规则，得:
$$FOLLOW(B)=FOLLOW(S)=\{a,\#\}$$
第四个求B${}^{‘}$的FOLLOW集，从产生式的右侧找到B${}^{‘}$, (B $\to$ DB${}^{‘}$), 根据第三条规则，得:
$$FOLLOW(B^{‘})=FOLLOW(B)=\{a,\#\}$$
第五个求D的FOLLOW集，从产生式的右侧找到D, (B $\to$ DB${}^{‘}$), 根据第二条规则，得:
$$FOLLOW(D)=FIRST(B^{‘})\setminus |ϵ|=\{b\}$$
又因为B${}^{‘}\to ϵ$, 根据 B $\to$ DB${}^{‘}$ 和第三条规则，得:
$$FOLLOW(D)=FOLLOW(B)=\{b,a,\#\}$$

生成预期分析表算法

1. 对于文法G的每个产生式 A $\to \alpha$, 执行第2步和第3步
2. 对每个终结符a $\in$ FIRST($\alpha$), 把 A $\to \alpha$ 加至 M[A, a]中
3. 若 $ϵ\in$ FIRST($\alpha$), 则对任何b $\in$ FOLLOW(A) 把 A $\to \alpha$ 加至 M[A, b]中

note:
每个产生式的意思是将所有含“|”的产生式全部展开，然后看每个产生式的FIRST集，如果这个FIRST集中有“$ϵ$”, 那就要将这个产生式加入到 FOLLOW集中相应符号中

例题

已知文法G如下:
             S $\to$ AB
             A $\to$ Ba | $ϵ$
             B $\to$ Db | D
             D $\to$ d | $ϵ$
(1) 构建文法G的LL(1)分析表
(2) 判断句子adb是否为有效文法产生的语言，并给出分析过程

因为 S $\Rightarrow$ A $\Rightarrow$ B $\Rightarrow$ D $\Rightarrow ̸$ S, 所以不存在左递归
因为将 A $\to$ Ba | $ϵ$ 代入到 S $\to$ AB 会含有回溯，B $\to$ Db | D 这条产生式本身也含有回溯，所以要先消除回溯

消除左递归(本题不需要消除左递归)：
P的产生式: P $\to$ Pa${}_1$ | Pa${}_2$ | … | Pa${}_m$ | ${\beta }_1$ | ${\beta }_2$ | … | ${\beta }_n$
其中，每个a不等于$ϵ$, 每个$\beta$不以P开头
       P $\to {\beta }_1{P}^{‘}$ | ${\beta }_2{P}^{‘}$ | … | ${\beta }_n{P}^{‘}$
       P${}^{‘}\to a_1{P}^{‘}$ | $a_2{P}^{‘}$ | … | $a_m{P}^{‘}$

消除回溯(提左因子)
A的规则是: A $\to \delta {\beta }_1$ | $\delta {\beta }_2$ | … | $\delta {\beta }_n$ | ${\gamma }_1$ | ${\gamma }_2$ | … | ${\gamma }_m$
其中，每个$\gamma$不以$\delta$开头
       A $\to \delta A^{‘}$ | ${\gamma }_1$ | ${\gamma }_2$ | … | ${\gamma }_m$
       A${}^{‘}\to {\beta }_1$ | ${\beta }_2$ | … | ${\beta }_n$

通过消除回溯，将文法改写为:
             S $\to$ BS${}^{‘}$
             S${}^{‘}\to$ aB | $ϵ$
             B $\to$ DB${}^{‘}$
             B${}^{‘}\to$ b | $ϵ$
             D $\to$ d | $ϵ$

通过拆分上边的产生式，得到：

1. S $\to$ BS${}^{‘}$
2. S${}^{‘}\to$ aB
3. S${}^{‘}\to ϵ$
4. B $\to$ DB${}^{‘}$
5. B${}^{‘}\to$ b
6. B${}^{‘}\to ϵ$
7. D $\to$ d
8. D $\to ϵ$

先看这八个产生式的FIRST集，如果FIRST集中有$ϵ$, 就要看相应产生式的FOLLOW集(例如产生式3、6、8)

终结符: {a, b, d, #}
非终结符: {S, S${}^{‘}$, B, B${}^{‘}$, D}

FIRST(S) = {a, b, d, $ϵ$}      FOLLOW(S) = {#}
FIRST(S${}^{‘}$) = {a, $ϵ$}             FOLLOW(S${}^{‘}$) = {#}
FIRST(B) = {d, b, $ϵ$}          FOLLOW(B) = {a, #}
FIRST(B${}^{‘}$) = {b, $ϵ$}             FOLLOW(B${}^{‘}$) = {a, #}
FIRST(D) = {d, $ϵ$}              FOLLOW(D) = {b, a, #}

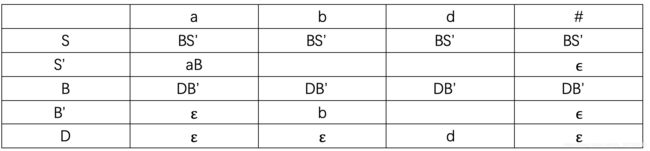
解释：
先看S这一行，因为第一条产生式 FIRST(BS${}^{‘}$) = {a, b, d, $ϵ$}，所以根据第二条规则，在a, b, d列填入BS${}^{‘}$，又因为$ϵ\in$ FIRST(BS${}^{‘}$), 所以还要看S的FOLLOW集，FOLLOW(S) = {#}，所以在#这一列也填入BS${}^{‘}$
看S${}^{‘}$这一行，第二条产生式 FIRST(aB) = {a}, 根据第二条规则，在a这一列填入aB
又因为第三条产生式S${}^{‘}\to ϵ$, $ϵ\in$ FIRST(S${}^{‘}$), 所以看S${}^{‘}$的FOLLOW集，FOLLOW(S${}^{‘}$) = {#}, 所以在#这一列填入$ϵ$ (这个 $ϵ$ 由S${}^{‘}\to ϵ$这条产生式得出)
看B这一行，因为第四条产生式 FIRST(DB${}^{‘}$) = {d, b, $ϵ$}, 根据第二条规则，在d, b列填入DB${}^{‘}$, 又因为 $ϵ\in$ FIRST(DB${}^{‘}$), 所以看B的FOLLOW集，因为FOLLOW(B) = {a, #}, 所以在a, #列填入DB${}^{‘}$
看B${}^{‘}$这一行，因为第五条产生式 FIRST(b) = {b}, 所以在b列填入b
又因为第六条产生式B${}^{‘}\to ϵ$, $ϵ\in$ FIRST(B${}^{‘}$), 所以看B${}^{‘}$的FOLLOW集，FOLLOW(B${}^{‘}$) = {a, #}, 所以在a, #列填入$ϵ$
看D这一行，因为第七条产生式 FIRST(d) = {d}, 所以在d列填入d
又因为第八条产生式 D $\to ϵ$, $ϵ\in$ FIRST(D), 所以看D的FOLLOW集，FOLLOW(D) = {a, b, #}, 所以在a, b, #列填入$ϵ$

分析句子

栈STACK用于存放文法符号。分析开始时，栈底先放一个’#’, 然后，放进文法开始符号。同时，假定输入串之后也总有一个‘#’，标志输入串结束

对于任何(X, a), 总控程序每次都执行下述三种可能的动作之一

1. 若 X = a = ‘#’, 则宣布分析成功，停止分析过程
2. 若 X = a =$̸$ ‘#’, 则把X从STACK栈顶逐出，让a指向下一个输入符号
3. 若 X 是一个非终结符，则查看分析表M，若 M[A, a] 中存放着关于X的一个产生式，那么，首先把X逐出STACK栈顶，然后，把产生式的右部符号串按反序推进STACK栈（若右部符号为$ϵ$, 则意味不推什么东西进栈）
   
   解释：
   将开始符号S放入栈顶，要分析的句子放入输入，看分析表，当S遇到a时，根据第三条规则，执行 S $\to$ BS${}^{‘}$ ,将S从栈顶逐出，将BS${}^{‘}$按反序推进栈，得到S${}^{‘}$B，看分析条，当B遇到a，根据第三条规则，执行 B $\to$ DB${}^{‘}$, 将B从栈顶逐出，将DB${}^{‘}$按反序推进栈，得到B${}^{‘}$D, 看分析表 …(依此类推)，当分析栈为终结符时，则根据第二条规则，分析栈栈顶和输入串第一个字符进行抵消，当分析栈栈顶为‘#’，且输入串为‘#’时，则宣布分析成功，停止分析过程