Leetcode--堆类型题总结(单堆与双堆)
目录
1.C++中的堆实现
2.单堆问题
3.双堆问题
1.C++中的堆实现
可以直接用优先级队列priority_queue
默认是大顶堆 priority_queue
小顶堆 priority_queue
也可以使用 multiset (使用multiset的情况一般为 需要从堆中删除元素,因为priority_queue的方法中没有 erase方法)
默认是大顶堆 multiset
小顶堆 multiset
2.单堆问题
指通过一个堆就可以解决的问题
一般这种问题都具有以下特点:
求解第/前 k个最大,最小或是最频繁的元素;都可以使用堆来实现 (而不用通过排序实现)
模式:
确定大顶堆还是小顶堆
比如求 第K个最大元素,我们就用 大小为K的小顶堆,遍历数组完毕后,小顶堆堆顶元素即为第K个最大元素
遍历数组,压入小顶堆,判断小顶堆的元素个数,如果大于k,则弹出,保证小顶堆内元素个数始终是 k个
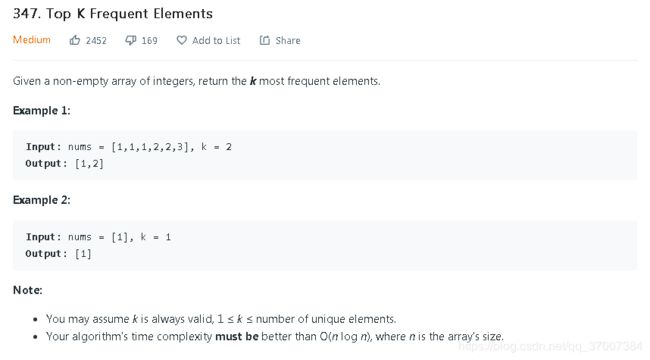
对于最频繁或是最不频繁的元素问题:可以首先结合 pair
priority_queue
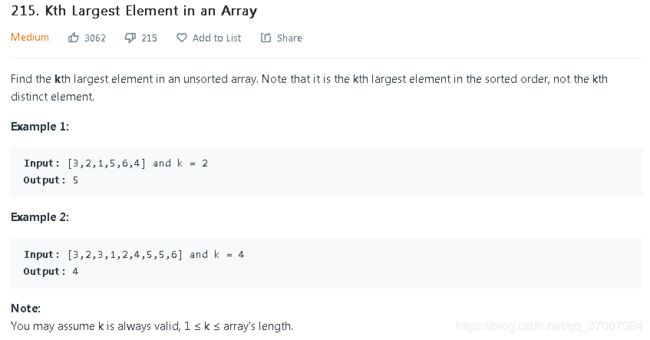
比如:寻找第k个最大元素
求第k个最大元素,我们保留下来前k个最大元素即可,而前k个元素中我们又要最小的一个,所以我们可以使用小顶堆
保证小顶堆元素内个数不超过k即可,因为 随着我们压入元素,堆的大小增大,而小元素 一定在堆顶,所以 当堆的大小超过k时,就会 pop出去小元素,最后堆中剩下前k个大元素
class Solution {
public:
int findKthLargest(vector& nums, int k) {
for(auto i : nums)
{
minheap.push(i);
if(minheap.size() > k)
{
minheap.pop();
}
}
return minheap.top();
}
private:
priority_queue,greater> minheap;
}; class Solution {
public:
vector topKFrequent(vector& nums, int k)
{
unordered_map map;
vector res;
for(int i = 0; i < nums.size(); i++)//统计每个元素的出现的频率
{
map[nums[i]]++;
}
priority_queue,vector>,less>> pq; //用大顶堆来记录 频率和对应元素,
//用pair的第一个元素代表频率,第二个元素代表对应该频率对应的元素
for(auto it = map.begin(); it != map.end(); it++)
{
pq.push(make_pair(it->second,it->first));
if(pq.size() > map.size()-k)
{
res.push_back(pq.top().second);
pq.pop();
}
}
return res;
}
}; 3.双堆问题
指通过两个堆相互配合解决问题
特点:
被告知,我们拿到一大把可以分成两队的数字。怎么把数字分成两半?使得:小的数字都放在一起,大的放在另外一半。双堆模式就能高效解决此类问题。然后通过小顶堆寻找最小数据,大顶堆寻找堆中最大数据
这样中位数就可以通过 小顶堆和大顶堆堆顶元素求出
模式:
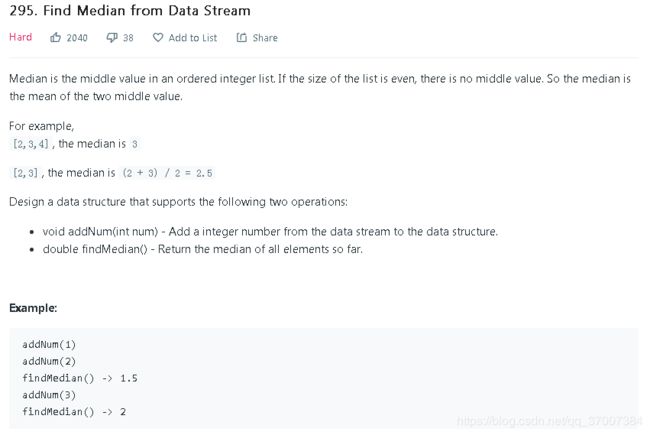
比如求 数据流中的 中位数,因为 数据流一直在增加,所以如果采用排序,那么每一次增加元素后均需要再次排序,时间复杂度过高; 由于中位数 只需要知道中间两个数(或一个数)即可求出
我们可以使用 大顶堆 来存储 数据流中的 一半较小元素;用 小顶堆来存储 数据流中的 一般较大元素;
且保证 大顶堆的大小 大于 等于 小顶堆的大小,这样 如果 数据流大小为奇数,则返回 大顶堆 的堆顶元素即可,如果数据流大小为偶数,则 大顶堆和小顶堆元素取平均即可
如何实现?
//已知此时数据流元素个数为2k,大顶堆中存储较小元素,大顶堆存储较大元素
maxheap.push(val);//此时堆顶为大元素
将大元素 压入 小顶堆中
minheap.push(maxheap.top())
maxheap.pop()//从大顶堆中删除
//且要保证 大顶堆的大小不小于 小顶堆大小
while(maxheap.size() < minheap.size()) {将 小顶堆中元素压入大顶堆}
//最后通过验证数据流大小 来求中位数即可
class MedianFinder {
public:
/** initialize your data structure here. */
MedianFinder() {
}
void addNum(int num) {
maxheap.push(num);//将所有数压入大顶堆
minheap.push(maxheap.top());// 将 大顶堆中的最大元素压入最小堆
maxheap.pop();
//同时要保持,maxheap的大小比 minheap大或者相等
if(maxheap.size() < minheap.size())
{
maxheap.push(minheap.top());
minheap.pop();
}
}
double findMedian() {
if(minheap.size() != maxheap.size())
{
return maxheap.top();
}
return (minheap.top()+maxheap.top())*0.5;
}
private:
priority_queue maxheap;//大顶堆 ,装 小一部分的数,始终保持大顶堆中多一个数
priority_queue,greater> minheap;//小顶堆,装 比较大一部分的数
};
/**
* Your MedianFinder object will be instantiated and called as such:
* MedianFinder* obj = new MedianFinder();
* obj->addNum(num);
* double param_2 = obj->findMedian();
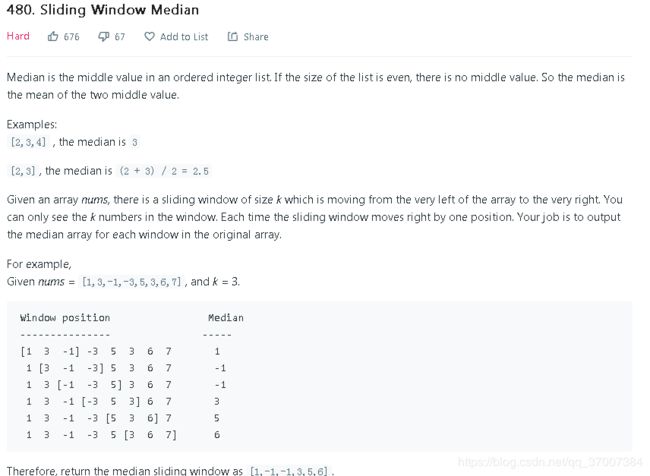
*/ 这里由于是滑动窗口,也就是说 两个堆里面的总元素是有删减的,所以不能再用 priority_queue,因为其中没有 erase方法
我们可以使用 multiset来实现堆内元素的删减
然后结合固定滑动窗口法即可(逐渐改变滑动窗口内元素即可)
详细代码如下:
class Solution {
public:
vector medianSlidingWindow(vector& nums, int k) {
vector res;
for(int i = 0; i < k; i++)
{
maxheap.insert(nums[i]);
minheap.insert(*maxheap.begin());
maxheap.erase(maxheap.begin());
if(maxheap.size() < minheap.size())
{
maxheap.insert(*minheap.begin());
minheap.erase(minheap.begin());
}
}//初始的大顶堆与小顶堆
if(k%2 == 0)
{
res.push_back((*minheap.begin() * 0.5 +*maxheap.begin() *0.5));
}
else
{
res.push_back(*maxheap.begin());
}
//开始移动滑动窗口,并改变大小顶堆内元素
for(int i = 0; i < nums.size()-k; i++)
{
//删除左窗口元素,因为已经开始移动
if(maxheap.find(nums[i]) != maxheap.end())
{
maxheap.erase(maxheap.find(nums[i]));
}
else if(minheap.find(nums[i]) != minheap.end())
{
minheap.erase(minheap.find(nums[i]));
}
//开始添加一个右窗口元素
maxheap.insert(nums[i+k]);
minheap.insert(*maxheap.begin());
maxheap.erase(maxheap.begin());
while(maxheap.size() < minheap.size())
{
maxheap.insert(*minheap.begin());
minheap.erase(minheap.begin());
}
if(k%2 == 0)
{
res.push_back((*minheap.begin() * 0.5 +*maxheap.begin() *0.5));
}
else
{
res.push_back(*maxheap.begin());
}
}
return res;
}
private:
multiset minheap;//升序,begin处最小
multiset> maxheap;//降序,begin()最大
};