EOJ Monthly 2018.12 C---她的名字
对于每一次询问，可以分为两个部分：①以XY结尾有多少种可能；②对于每一种XY，从X之前的所有数选出N-2个数有多少种可能，就是它的组合数。
对于某一S，解决任意询问【N、X、Y】：
|S|
首先解决①，由于②与X在S中位置有关，因而可以枚举S的所有位置i与Y(0~9，Y必须在i后)的组合数pos[i][Y]；这时可以预处理出0~9在S中所有的出现位置V[i]，使用时可以进行二分搜索，找到第一个位置比i后的Y，它在V中的位置是k，pos[i][Y]=V[Y].size()-k
然后解决②，当前X在S的位置是i，很明显有res[N][X][Y]+=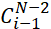
*pos[i][Y]，求组合数可以使用Pascal公式
和
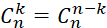
最后对于所有询问，常数时间内就能出结果
#include
#define For(i,x,y) for(int i=(x);i<=(y);++i)
#define Fov(i,x,y) for(int i=(x);i>=(y);--i)
#define Fo(i,x,y) for(int i=(x);i<(y);++i)
#define midf(a,b) ((a)+(b)>>1)
#define L(_) (_)<<1
#define R(_) ((_)<<1)|1
#define fi first
#define se second
#define ss(_) scanf("%s",_)
#define si(_) scanf("%d",&_)
#define sii(x,y) scanf("%d%d",&x,&y)
#define siii(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define sl(_) scanf("%lld",&_)
#define mem(x,y) memset(x,y,sizeof(x))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pairP;
inline int read()
{
char ch=getchar(); int x=0, f=1;
while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar();}
while('0'<=ch&&ch<='9') { x=x*10+ch-'0'; ch=getchar();}
return x*f;
}
const int inf=0x3f3f3f3f;
const double pi=acos(-1.0);
const ll mod=1e9+7;
const int n_max=2e3+10;
char s[n_max];
vectorV[10];
ll comb[n_max][n_max],pos[n_max][10],res[n_max][10][10];
int main()
{
//freopen("in.txt","r",stdin);
comb[0][0]=1;
Fo(i,1,n_max)
{
comb[i][i]=comb[i][0]=1;
For(j,1,i/2) comb[i][j]=comb[i][i-j]=(comb[i-1][j-1]+comb[i-1][j])%mod;
}
ss(s+1);
int n=strlen(s+1),q,x,y;
For(i,1,n) V[s[i]-'0'].push_back(i);
si(q);
For(i,1,n-1)
{
For(j,0,9)
{
int t=V[j].size();
if(V[j].size()==0||V[j][t-1]<=i) continue;
int k=upper_bound(V[j].begin(),V[j].end(),i)-V[j].begin();
pos[i][j]=t-k;
}
}
For(i,2,n)
{
int num=i-2;
For(j,1,n-1)
{
int t=s[j]-'0';
if(comb[j-1][num]==0) continue;
For(k,0,9)
{
if(pos[j][k]==0) continue;
res[i][t][k]=(res[i][t][k]+comb[j-1][num]*pos[j][k])%mod;
}
}
}
For(i,1,q)
{
sii(x,y);
int t1=y/10,t2=y%10,nt=V[t1].size();
if(x>n)
{
printf("0\n");
continue;
}
printf("%lld\n",res[x][t1][t2]);
}
return 0;
}
