【数据结构】二叉树的定义及其遍历
文章目录
- 二叉树的定义
- 二叉树的几个重要性质
- 确定二叉树
- 二叉树的存储结构
- 1. 顺序存储结构
- 2. 链表存储
- 二叉树的遍历(递归)
- 二叉树的非递归遍历
- 中序遍历非递归遍历算法
- 先序遍历的非递归算法
- 后序非递归遍历
- 二叉树的层次遍历
- 二叉树层次遍历II
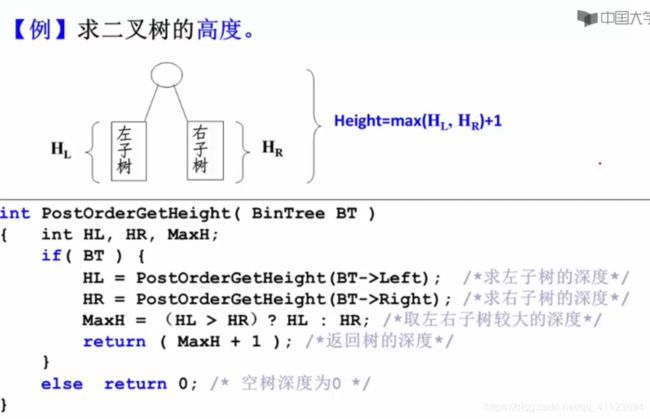
- 求二叉树高度
二叉树的定义
二叉树T: 一个有穷的结点集合。
这个集合可以为空,若不为空,则他由根节点和称为其左子树Tleft和右子树Tright的两个不相交的二叉树组成。
- 二叉树有五种基本形态
- 空
- 根结点
- 根结点+左子树
- 根结点+右子树
- 根结点+双子树
- 二叉树的子树有左右之分
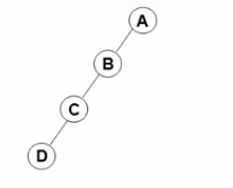
- 斜二叉树
- 完美二叉树/满二叉树
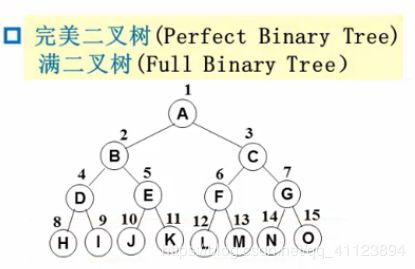
有n个结点的二叉树,对树中结点按从上至下,从左至右顺序进行编号
二叉树的几个重要性质
- 一个二叉树的第i层的最大节点数未:2^(i-1),i>=1>。
- 深度为k的二叉树有最大结点个总数:2^k -1
- 对任何非空二叉树T,若n0表示叶子结点个数、n2是度为2的非叶子结点总个数,那么二者满足关系n0=n2 +1 ;
证明:对这样的二叉树,除了根节点以外,每个节点都有且仅有一条边,边的总数:
n0+n1+n2-1 = 0 X n0 + 1 X n1+2 X n2 - 拓展:m叉树中各类结点数之间的关系
在二叉树中,我们知道叶结点总数n0与有两个儿子的结点n2总数之间的关系是:n0=n2+1.
那么类似关系是否可以推广到m叉树中?也就是,如果在m叉树中,叶结点总数是n0,有一个儿子的结点总数是n1,有2个儿子的结点总数是n2,有3个儿子的结点总数是n3,…。那么,之间存在什么关系?
n0=n2+2n3+3n4+…+(i-1)n(i-1)
确定二叉树
必须要有中序遍历才能确定二叉树
- 先序和中序遍历来确定一颗二叉树
- 【分析】
- 根据先序遍历序列第一个结点确定根节点
- 根据根结点在中序遍历序列中分割出左右两个子序列
- 对左子树和右子树分别递归使用相同的方法继续分解
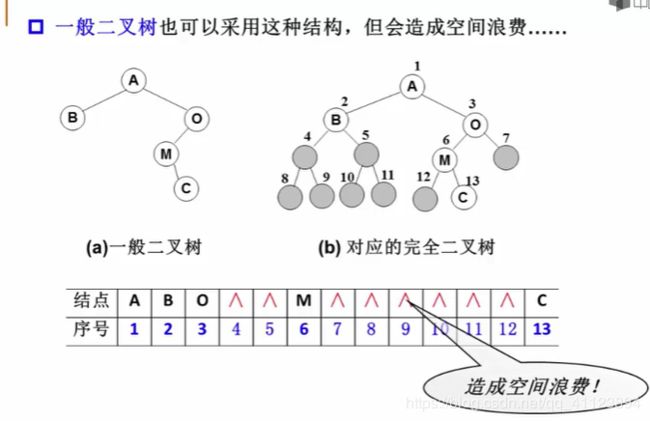
二叉树的存储结构
1. 顺序存储结构
完全二叉树: 按从上至下、从左至右的顺序存储n个结点的完全二叉树。

2. 链表存储
typedef struct TreeNode *BinTree;
typedef BinTree Position;
struct TreeNode{
ElementType Data;
BinTree Left;
BinTree Right;
}
二叉树的遍历(递归)
- 先序遍历
遍历过程为:- 访问根节点
- 先序遍历其左子树
- 先序遍历其右子树
void PreOrderTravversal(BinTree BT){
if(BT){
printf("%d",BT->data);
PreOrderTraversal(BT->left);
PreOrderTraversal(BT->rigth);
}
}
- 中序遍历
void PreOrderTravversal(BinTree BT){
if(BT){
PreOrderTraversal(BT->left);
printf("%d",BT->data);
PreOrderTraversal(BT->rigth);
}
}
- 后序遍历
void PreOrderTravversal(BinTree BT){
if(BT){
PreOrderTraversal(BT->left);
PreOrderTraversal(BT->rigth);
printf("%d",BT->data);
}
}
二叉树的非递归遍历
中序遍历非递归遍历算法
非递归算法实现的基本思路:使用堆栈
- 遇到一个结点,就把他压栈,并去遍历它的左子树
- 当左子树遍历结束后,从栈顶弹出这个结点并访问它
- 然后按其右指针再去中序遍历该结点的右子树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
if(!root ){return vector<int>();}
stack<TreeNode*>st;
vector<int>ret;
TreeNode *p = root;
while(p||!st.empty()){
while(p){
st.push(p);
p=p->left;
}
p=st.top();
st.pop();
ret.push_back(p->val);
p=p->right;
}
return ret;
}
};
先序遍历的非递归算法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
if(!root)return vector<int>();//空树,直接返回
stack<TreeNode*> st;
vector<int> ret;
TreeNode* p=root;//p指向当前访问结点
while(p||!st.empty())
{
while(p){//若当前结点非空
ret.push_back(p->val);//访问该结点
st.push(p);//记录该结点到栈,后面回退
p=p->left;//进入左子树访问
}
// while条件的设置,保证下面st非空
//若p非空,那么一定会压入新元素,此时st非空。若p为空,则st一定非空
//按先序的,此时父节点已经访问,通过它拿到右孩子后就可以移除
p=st.top();st.pop();
p=p->right;//进入右子树访问
}
return ret;
}
};
后序非递归遍历
讨论3.4 如何用堆栈实现后序遍历的非递归程序老师参与
我们前面看到,借助堆栈可以实现前序遍历、中序遍历的非递归程序,而且两者的程序结构几乎一样。
那么,是否也可以借助堆栈实现后序遍历的非递归程序?是不是挪动一下printf语句就可以了?
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> stk1,stk2;
if(root==NULL)
return res;
stk1.push(root);
TreeNode* temp;
while(!stk1.empty()){
temp=stk1.top();
stk1.pop();
stk2.push(temp);
if(temp->left!=NULL)
stk1.push(temp->left);
if(temp->right!=NULL)
stk1.push(temp->right);
}
while(!stk2.empty()){
res.push_back(stk2.top()->val);
stk2.pop();
}
return res;
}
};
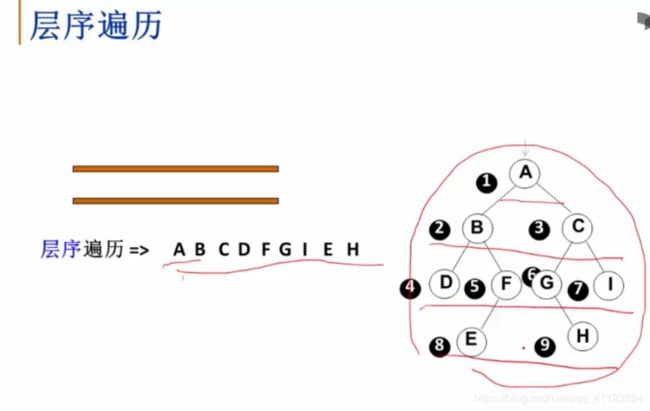
二叉树的层次遍历
二叉树遍历的核心问题:二维结构的线性化
- 从结点访问其左、 右儿子结点
- 访问左儿子后,右儿子结点怎么办?
- 需要一个存储结构保存暂时不访问的结点
- 存储结构:堆栈、队列
队列实现:
遍历从根节点开始,首先将根结点入队,然后开始执行循环:结点出队、访问该结点、其左右儿子入队
基本过程:
先根结点入队,然后:
void levelOrderTraversal(BinTree BT)
{
Queue Q;
BinTree T;
if(!BT)return;//空树则直接返回
Q=CreateQueue(MaxSize);
AddQ(Q,BT);
while(!isEmptyQ(Q)){
T=DeleteQ(Q);
printf("%d\n",T->data);
if(T->left)AddQ(Q,T->Left);
if(T->Right)AddQ(Q,T->Right);
}
leetcode:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;
if(!root){
return res;
}
queue<TreeNode*> Q;
TreeNode* p;
Q.push(root);
while(Q.empty()==0){
vector<int> a;
int width=Q.size();
for(int i=0;i<width;i++){
p=Q.front();
a.push_back(p->val);
Q.pop();
if(p->left) Q.push(p->left);
if(p->right) Q.push(p->right);
}
res.push_back(a);
}
return res;
}
};
二叉树层次遍历II
Given a binary tree, return the bottom-up level order traversal of its nodes’ values. (ie, from left to right, level by level from leaf to root).
For example:
Given binary tree [3,9,20,null,null,15,7],
print:
[
[15,7],
[9,20],
[3]
]
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
queue<TreeNode*>Q;
vector<vector<int>>res;
TreeNode *p;
if(!root){
return res;
}
Q.push(root);
while(Q.empty() == 0)
{
vector<int>a;
int width = Q.size();
for(int i = 0 ; i < width;i++){
p= Q.front();
a.push_back(p->val);
Q.pop();
if(p->left){Q.push(p->left);}
if(p->right){Q.push(p->right);}
}
res.insert(res.begin(),a);
}
return res;
}
};