对1976年Diffie和Hellman的文章《New Direction in Cryptography》的中文翻译

中文翻译（1976-Diffie-Hellman)

密码学新方向

摘要

​ 本文介绍了两种当前密码学的发展技术。远程处理的广泛应用导致了对新型密码系统的需求，这种系统可以最大限度地减少对安全密钥分发通道的需求，并且提供与手写签名等效的方法。本文提出了解决这些问题的方法。文中还讨论了通信和计算理论是如何开始为解决长期存在的密码问题提供工具的。

I、引言

​ 今天我们站在密码学革命的边缘。廉价数字硬件的发展使其摆脱了机械计算的设计限制，并将高级密码设备的成本降低到可用于远程提款机和计算机终端等商业应用的水平。反过来，这样的应用程序产生了对新类型密码系统的需求，这些系统将安全密钥分发通道的需求降至最低，并提供与手写签名等效的签名。同时，信息理论和计算机科学的理论发展显示出提供可证明的安全密码系统的希望，将这门古老的艺术转变为一门科学。

​ 计算机控制通信网络的发展使世界各地的人们或计算机之间的联系变得不费吹灰之力和成本低廉，远程通信取代了大多数邮件和许多短途旅行。在许多应用中，必须保证这些联系人的安全，防止窃听和非法信息的注入。然而，目前安全问题的解决远远落后于其他通信技术领域。现代的加密技术已经不能满足要求，因为它的使用会给系统用户带来严重的不便，从而消除了远程处理（带来）的许多好处。

​ 最著名的密码学问题是：防止未经授权（的用户）从不安全信道上的通信中提取信息。然而，为了使用密码学来保证隐私，目前通信双方必须共享一个别人不知道的密钥。这是通过预先通过某些安全通道（如私人快递或挂号信）发送密钥来完成的。然而，在商业中，两个之前不认识的人之间的秘密谈话是常见的，而且期望最初的商业接触推迟到足够长的时间，以便通过某种物理方式传输密钥是不现实的。这个密钥分配问题所带来的成本和延迟是将业务通信转移到大型远程处理网络的主要障碍。

​ 第三节提出了两种在不影响系统安全的情况下通过公共（即不安全）信道传输密钥信息的方法。在公钥密码系统中，加密和解密由不同的密钥E和D控制，因此从E计算D在计算上是不可行的（例如，需要$10^{100}$条指令）。可以在不损害解密密钥D的情况下公开加密密钥E。网络的每个用户可以将其加密密钥放在公共目录中。这使得系统的任何用户都可以将消息以加密的方式发送给任何其他用户，这样只有预期的接收者才能解密消息。因此，公钥密码系统是一种多址密码。不管两个人以前有没有交流过，他们之间都可以进行私人谈话。每一个发送者用接收者的公钥加密信息给接收者，解密人（接收者）使用自己的秘钥解密接收到的信息。

​ 我们提出了一些开发公钥密码系统的技术，但是这些技术仍然在很大程度上值得商榷。

​ 公钥分发系统提供了一种不同的解决方案，以消除对安全密钥分发通道的需求。在这样一个系统中，希望交换密钥的两个用户来回通信，直到他们得到一个共同的密钥。如果第三方窃听到这种交换，则必须发现它，并从所听到的信息中计算密钥在计算上是不可行的，第三节给出了公钥分配问题的一种可能的解决方案，并且Merkle[1]提出了不同形式的部分解决方案。

​ 第二个问题，阻碍了目前商业交流发展的是远程处理系统中的认证问题，可以用密码学方案来解决。当前的业务中，合同的有效性是由签名来保证的。已签署的合同是协议的法律证据，持有人可以在必要时出庭。使用签名，无论如何，都需要传输和存储书面合同。为了能够完全数字化地替换本文所述的密钥源，每个用户必须能够生成任何人都可以检查其真实性的消息，如图1是传统密码系统中的信息流。但不可能被其他人，甚至是收信人产生。由于只有一个人可以发起消息，但许多人可以接收消息，因此可以将其视为广播密码。目前的电子认证技术不能满足这一需求。

​ 第四节讨论了提供真实的、数字的、依赖于消息的签名方案。出于上述原因，我们将此称为单向身份验证问题。给出了部分解，并给出了如何将任意公钥密码体制转换为单向认证体制。

​ 第五节将考虑各种密码问题之间的相互关系，并介绍更困难的陷阱门问题。

​ 同时，通信和计算也产生了新的密码问题，它们的发展，信息论和计算论开始为解决经典密码学中的重要问题提供工具。

​ 寻求不可破解的密码是密码学研究中最古老的主题之一，但直到本世纪，所有提出的系统最终都被破解。然而，在二十世纪二十年代，“一次一密”被提出，并且被证明是牢不可破的[2，第398-400页]。这一系统和相关系统的理论基础在四分之一世纪之后为信息论（3）奠定了坚实的基础。“一次一密”需要非常长的密钥，因此在大多数应用中非常昂贵。

​ 相比之下，大多数密码系统的安全性在于密码分析员在不知道密钥的情况下破解明文在计算上困难的。这个问题属于计算复杂性和算法分析的范畴，这是最近两个研究解决计算问题困难的学科。利用这些理论的结果，可以在可预见的将来将安全性证明扩展到更有用的系统类别。第六节探讨了这种可能性。

​ 在进行方案介绍之前，我们将在下一节介绍术语并定义威胁环境。

II、传统密码学

​ 密码学是解决两类安全问题的“数学的系统”学科：隐私和认证。隐私系统防止在不安全的信道上传输消息时被未经授权者从中获取信息，从而确保发送者发送的消息只能被预期的接收者读取。身份验证系统防止未经授权将消息注入公共通道，从而确保消息的接收者验证其发送者的合法性。

​ 如果信道的安全性不能满足用户的需求，则该信道被认为是公共的。因此，某些用户可能认为诸如电话线之类的信道是私有的，而某些用户则认为信道是公共的。根据使用情况，任何频道都可能受到窃听或注入的威胁。在电话通信中，注入的威胁是最主要的，因为被叫方不能确定哪部电话正在被呼叫。窃听，这需要使用窃听装置，技术上更困难，法律上更危险。相比之下，在广播中，这种情况是相反的。窃听是被动的，不涉及法律风险，而注入则暴露了窃听者，并且可能被起诉。

​ 我们的问题被分为隐私和身份验证问题之后，我们有时会进一步将身份验证细分为消息身份验证（这是上面定义的问题）和用户身份验证（其中，系统的唯一任务是验证此人是否是信息认证的人）。例如，出示信用卡的个人身份必须得到核实，但他不希望传递任何信息。尽管用户身份验证中明显没有消息，但这两个问题在很大程度上是等价的。在用户身份验证中，有一个隐含的消息“我是用户X”，而消息身份验证只是验证发送消息的一方的身份。然而，在环境威胁和这两个子问题的其他方面的差异有时使区分它们变得方便。

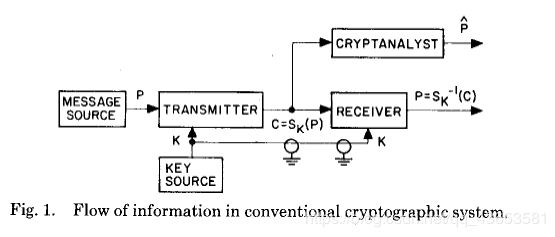
​ 图1说明了用于通信隐私的传统密码系统中的信息流。有三方：发射者、接收者和窃听者。发送者生成纯文本或未加密的消息P，以通过不安全的信道传送到合法的接收者。为了防止窃听者获取P，发送者在P上用可逆变换SK来产生密文或密码$C＝S_K（P）$。密钥通过一个安全信道传输给合法接收者，由图1中的屏蔽路径表示。只有合法接收者知道密钥K，他能够通过$S_K^{-1}(C)=S_K^{-1}(S_K(P))=P$得到原始明文P。安全的信道由于容量或延迟的原因不能被用来传送P本身。例如，安全通道可能是每周的信使，而不安全通道可能是电话线。

​ 一个密码系统是一个可逆变换的单个参数族 {S_K}，K∈{K}

S_K：{P} → {C}

从一个明文空间（P）到一个密文空间（C）。参数K被称为密钥，从称为密钥空间的有限集{K}中选择。如果消息空间{P}和{C}相等，我们将用{M}来表示它们。在讨论单个密码转换S_K时，我们有时会忽略(密钥)系统，而只提及单个密钥。

​ 设计密码系统{S_K}的目的是使加密和解密操作便宜，但是要确保任何成功的密码分析操作都过于复杂而变得不经济。解决这个问题有两种方法。一个由于密码分析的计算成本而安全的系统，但是它会屈服于计算量不受限制的攻击，被称为计算安全；而一个能够抵抗任何密码分析攻击的系统，即允许的无限计算量，被称为无条件安全。在文献[3]和[4]中讨论了非理性安全系统，它属于信息论中的香农理论的一部分，香农理论关注的是在无限计算条件下获得的最优性能。

​ 无条件安全性是由于一个密码存在多个有意义的解。例如，由英文文本产生的简单替换密码"XMD"可以表示明文消息：now，and，etc。相比之下，计算安全的密码包含足够的信息来唯一地确定明文和密钥。它的安全性完全取决于计算它们的成本。

​ 唯一常用的无条件安全系统是“一次一密”，其中明文与随机选择的相同长度的密钥相结合。虽然这样的系统可以证明是安全的，但是需要大量的密钥，这使得它对于大多数应用程序来说是不切实际的。除非另有说明，本文讨论的是计算安全系统，因为它们更普遍适用。当我们谈到开发可证明安全的密码系统的必要性时，我们排除了那些难以使用的一次性密码系统。相反，我们认为系统只使用几百位的密钥，可以在少量的数字硬件或几百行软件中实现。

​ 如果用内存使用量或运行时间来衡量任务的成本是有限的，但又不可能很大，那么我们将其称为计算上不可行的任务。

​ 由于纠错码分为卷积码和分组码，密码系统可分为两大类：流密码和分组密码。流密码以小块（位或字符）的形式处理明文，通常产生一个伪随机位序列，该序列是模2加明文比特。块密码以纯自然的方式作用于大的文本块，这样输入块中的一个小的变化就会在结果输出中产生一个大的变化。本文主要讨论块密码，因为这种错误传播特性在许多认证应用中都很有价值。

​ 在一个认证系统中，密码学被用来保证消息对接收者的真实性。不仅要防止一个爱管闲事的人把新的、看起来真实的信息注入一个频道，而且要防止他把过去拷贝的旧信息组合起来，或者仅仅通过重复的方式，产生明显真实的信息。一般来说，旨在保证隐私的密码系统不会阻止这种后一种形式的恶作剧。

​ 为了保证消息的真实性，添加的信息不仅是消息和密钥的函数，而且是日期和时间的函数；例如，将日期和时间附加到每个消息并加密整个序列。这确保只有拥有密钥的人才能生成一条消息，当解密时，该消息将包含正确的日期和时间。然而，必须特意提及，在该系统中密文的微小变化会导致解密明文的大变化。这种有意的错误传播确保，如果故意在信道上注入噪声，将诸如“擦除文件7”的消息更改为诸如“擦除文件8”的不同消息，则它还将更正认证信息。然后，该消息将被视为不真实而拒绝。

​ 评估密码系统能力的第一步是对它们将受到的威胁进行分类。用于隐私或身份验证的密码系统可能会受到以下威胁。

​ 唯密文攻击是一种密码分析攻击，其中密码分析人员只拥有密文。

​ 已知明文攻击是一种密码分析攻击，其中密码分析人员拥有大量对应的明文和密文。

​ 选择明文攻击是一种密码分析攻击，在这种攻击下，密码分析人员可以提交自己选择的无限数量的明文消息，并检查生成的密码。

​ 在所有情况下，假设敌手知道正在使用的通用系统$\{S_K\}$，因为这些信息可以通过研究密码设备获得。虽然许多密码学用户试图对他们的设备保密，但许多商业应用不仅要求通用系统是公开的，而且要求它是标准的。

​ 唯密文攻击在现实中经常发生。密码分析员只使用所使用语言特性（例如，在英语中，字母e出现的时间占13%）和某些“可能”单词的统计性知识（例如，字母可能以“Dear Sir:”开头）。它是一个系统所能承受的最弱的威胁，任何屈服于它的系统都是完全不安全的。

​ 一个对已知明文攻击安全的系统，使用户不必对过去的信息保密，也不必在解密前对其进行解释。这对系统用户来说是一个不合理的负担，特别是在商业场合，产品公告或新闻稿可能会以加密的形式发送，以便日后公开披露。外交信函中的类似情况导致了许多所谓安全系统的崩溃。虽然已知明文攻击并不总是可能发生的，但它的发生频率足以使无法抵抗它的系统被认为是不安全的。

​ 选择明文攻击在现实中很难实现，但可以近似实现。例如，向竞争对手提交一份提案可能会导致他对提案进行加密，并将它传输到他的总部。一种针对选择明文攻击的安全密码，可以使用户不必担心对手是否可以在其系统中植入消息。

​ 为了证明系统是安全的，考虑更强大的密码分析威胁是合适的，因为这些威胁不仅给出了密码系统工作环境的更真实的模型，而且使得对系统强度的评估更加容易。在已知明文攻击或选择明文攻击下，许多系统很难用唯密文攻击进行分析。

​ 从这些定义中可以清楚地看到，密码分析是一个系统识别问题。已知明文攻击和选择明文攻击分别对应于被动和主动系统识别问题。与许多考虑系统识别的学科（如自动故障诊断）不同，密码学的目标是建立难以识别而不是容易识别的系统。

​ 选择明文攻击通常被称为敌我识别攻击（Identification friend or foe attack），这一术语起源于二战后密码“敌友识别”系统的发展。敌我识别系统使军用雷达能够自动区分敌机和友机。雷达向接收到挑战的飞机发送一个时变的挑战，用适当的密钥对其进行加密，然后将其发送回雷达。通过将此响应与正确加密的挑战版本进行比较，雷达可以识别友军飞机。当飞机越过敌人的领地时，敌人的密码分析员可以发起挑战并检查加密的响应，试图确定正在使用的身份验证密钥，从而对系统发起选定的明文攻击。实际上，这种威胁是通过限制挑战的形式来应对的，挑战的形式不必是不可预测的，仅仅只需要不重复。

​ 认证系统所面临的其他威胁是传统密码学无法解决的，需要借助于本文介绍的新思想和新技术。在多用户网络中，接收方通常是系统本身，这种情况会导致接收方的身份验证数据受到威胁。因此，接收方的密码表和其他身份验证数据比发送方(单个用户)的密码表和其他身份验证数据更容易被窃取。如后面所示，防止这种威胁的一些技术也可以防止争议的威胁。也就是说，一条消息可能被发送，但稍后被发送方或接收方拒绝。或者，任何一方都可能声称发送了一条消息，而实际上并没有发送。（这对）不可伪造的数字签名和凭证是必需的。例如，一个不诚实的股票经纪人可能试图通过伪造来自客户的订单来掩盖未经授权的买卖行为，或者客户可能会拒绝他实际上授权，但他后来发现这将造成损失的订单。我们将引入一些概念，这些概念允许接收者验证消息的真实性，但是防止他伪造真实的消息，从而保护接收者的身份验证数据不受威胁，同时也防止了争议的产生。

III、公钥加密技术

​ 如图1所示，密码学已经成为一种衍生的安全措施。一旦存在一个可以传输密钥的安全通道，通过对发送的消息进行加密，可以将安全性扩展到其他带宽更高或延迟更小的通道。其结果是将密码学的使用限制在那些预先为密码学安全做过准备的人之间的通信。

​ 为了开发大型、安全的电信系统，这一点必须改变。大量希望与其他所有用户秘密通信的用户，n个用户会导致需要产生(n - 1) * n / 2 对密钥对。假设一对不熟悉的用户能够等待某个安全物理方法发送密钥，或者预先储存所有(n - 1) * n / 2对密钥，这是不现实的。在另一篇论文中，作者考虑了一种保守的方法，这种方法不需要在密码学本身中进行新的开发，但是这涉及到安全性降低、不方便以及对初始连接协议的网络限制为星形配置。

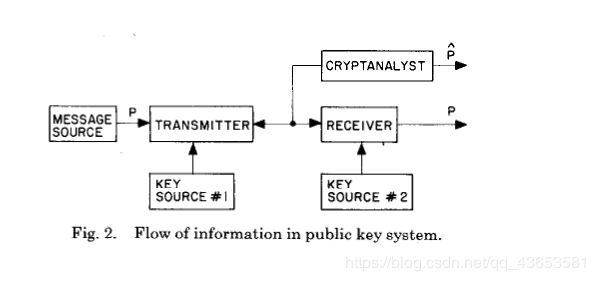
​ 我们建议可以开发如图2所示类型的系统，在这种系统中，双方仅通过公共通道通信，并且仅使用公共已知的技术可以创建安全连接。我们研究了两种方法去解决这个问题，分别称为公钥密码体制和公钥分发系统。第一种方法更强大，有助于解决下一节将讨论的身份验证问题，而第二种方法更接近于实现。公钥密码系统由一组{E_K | K ∈ {K} }和 {D_K | K ∈ {K}}组成，拥有可逆变换的算法，
$$\begin{gathered} E_k:\{M\}\to \{M\} \\ {D}_k:\{M\}\to \{M\} \end{gathered}$$
在有限的消息空间{ M }上，形如：

1. 对于任意的 K ∈ { K }，E_K 是 D_K 的倒数，
2. 对于任意的 K ∈ { K }和 M ∈ {M}，算法 E_K 和 D_K容易被计算，
3. 对于几乎每个K ∈ { K }，从E_K推导出与D_K等价且容易计算的算法在计算上是不可行的，
4. 对于每个K ∈ { K }，通过K计算逆对 E_K 和 D_k是可行的。

​ 由于第三个特性，用户的加密密钥 E_K 可以公开，而不影响其对应解密密钥 D_K 的安全性。因此，这个密码系统被分为两部分:一组加密变换和一组解密变换，这样，给定一个变换家族的成员，要找到另一个变换家族的对应成员是不可行的。

​ 第四个性质保证了在不限制加密或解密变换的情况下，有一种计算对应的反变换对的可行方法。在实践中，加密设备必须包含一个真正的随机数发生器(例如，一个有噪声的二极管)用于产生K，以及一个从其输出中生成E_K ~ D_K对的算法。

​ 对于这样一个系统，密钥分配问题被大大简化了。每个用户在其终端生成一对逆变换，即E和D。密钥D必须保密，而且不需要通过任何渠道传播。通过将加密密钥E与用户名和地址一起放在公共目录中，可以将其公开。然后任何人都可以对消息进行加密并将其发送给用户，但是（除了密钥D的拥有者）没有其他人可以破译其中的消息。因此，公钥密码系统可以看作是多址密码。

​ 关键是要保护加密密钥的公共文件不受未经授权的修改。由于文件的公共性质，这一任务变得更加容易。“读”保护是不必要的，而且，由于文件经常被修改，精心设计的“写”保护机制可以被经济地使用。

​ 公钥密码系统的一个有启发性的例子(尽管很不幸是无用的)是，将明文表示为二进制 n维向量 m，然后将其乘以一个可逆的二进制 n*n 矩阵E。因此，密文c = E m 让 D = E^-1，有 m = D c。因此，加密和解密都需要 n² 次操作。然而，从 E计算D涉及到一个矩阵的內积，这是一个困难问题。至少理论上获得任意一对逆矩阵比指定矩阵转化更容易。从单位矩阵 I 开始做初等行和列操作可以获得任意可逆矩阵E 。然后，为了获得 D = E^-1，从单位矩阵 I 开始做相同基本操作的逆操作。基本运算的顺序可以很容易地从一个随机的位串中确定出来。

​ 不幸的是，矩阵求逆需要大约 n³ 次操作。“密码分析”时间的比率(比如从E计算D)到加密或解密的时间最多为n，要获得10⁶ 或更大的比率，需要巨大的块大小。此外，从 I 中获得E的基本运算知识似乎并没有大大减少计算D的时间，而且，由于二进制算术中没有舍入误差，因此，在矩阵求逆中，数值稳定性并不重要。尽管这个矩阵示例缺乏实用性，但它仍然有助于阐述公钥密码系统中必要的关系。

​ 一种更实用的方法来寻找一对易于计算的逆算法E和D；因此，D很难从E中推断出来，可以利用分析低级语言程序的困难性。任何试图确定别人的机器语言程序完成了什么操作的人都知道E本身(即很难从E的算法中推断出它是做什么的)。如果程序通过添加不需要的变量和语句而故意造成混乱，那么确定逆算法就会变得非常困难。当然，E必须足够复杂，以防止从输入-输出对中识别它。

​ 本质上所需要的是一个单向编译器:它是采用用高级语言编写的容易理解的程序，并将其翻译成某种机器语言中难以理解的程序。编译器是单向的，因为进行编译必须是可行的，但是反向编译过程是不可行的。由于在这个应用程序中，程序大小和运行时的效率不是至关重要的，所以如果能够优化机器语言的结构来帮助解决这种混乱，那么这样的编译器是可能的。

​ Merkle [1] 独立地研究了在不安全信道上分配密钥的问题。他的方法与上面提到的公钥密码系统不同，将被称为公钥分发系统。目标是让两个用户(A和B)在不安全的信道上安全地交换密钥。然后，在正常的密码系统中，两个用户都可以使用这个密钥进行加密和解密。Merkle的解决方案，其密码分析成本以n² 增长，其中n是合法用户的成本。不幸的是，对于系统的合法用户来说，传输时间和计算时间的成本是一样的。因为Merkle的协议需要传输n个潜在密钥，然后才能确定一个密钥。这种高传输开销使该系统在实际应用中不能发挥太大的作用。如果将协议的开销限制为1兆比特，那么他的技术可以实现约10,000:1的成本比，这对于大多数应用程序来说都太小了。如果能够提供廉价、高带宽的数据链接，就可以达到100万比1或更大的比率，该系统将具有重大的实际价值。

​ 我们现在提出一种新的公钥分发系统，它有几个优点。首先，它只需要交换一个“密钥”。其次，密码分析者的工作量在合法用户的努力下呈指数增长。第三，它的使用可以绑定到用户信息的公共文件，该文件用于对用户A到用户B进行身份验证和相反验证（用户B到用户A）。通过使公共文件本质上成为只读内存，允许一个用户多次被多个用户验证其身份。Merkle的方案要求A和B通过其他方式验证彼此的身份。

​ 新方案利用了在元素素数为q的有限域GF(q)上计算对数的明显困难性。让
$$Y=a^{X}modq,1\le X\le q-1$$
当α 是有限域GF(q)上一个固定的元素，X 是以 α 为底的Y的对数，mod q：
$$X=lo{g}_{a}Ymodq,1\le Y\le q-1$$
根据X 计算 Y 是容易的，最多取 2 * log₂ q 次乘法[6，pp. 398-422]。例如，对于 X = 18，
$$Y=a^{18}=(((a^2{)}^2{)}^2{)}^2\times a^2$$
根据 Y 计算 X，可能要困难得多，对于精心挑选的q值，要求按照q^1/2次操作的顺序进行运算，使用最著名的算法[7，pp.9，575-576]，[8]。

​ 我们方案的安全性主要取决于计算对数 $modq$的难度，如果发现一个复杂度以$lo{g}_{2}q$ 增加的算法，我们的系统就会崩溃。虽然为了问题陈述的简单性可能允许这样简单的算法，但这可能导致证明问题时的困难性。现在，我们假设计算$logsmodq$的最著名的算法实际上接近于最优，因此，对于合适的$q$的选择, $q^{1/2}$是一个很好度量问题复杂性的方法。

​ 每个用户生成一个独立的随机数X_i, X_i从整数集{1,2，…，q - 1}中选择。每个用户都对X_i保密，但将
$$Y_i=a^{X_i}modq$$
以及他的姓名和地址放在一个公共目录下。当用户 $i$ 与 用户 $j$ 希望隐私通信时，他们使用
$$K_{ij}=a^{X_i{X}_j}modq$$
作为他们的密钥。用户 $i$ 通过从公共目录中获取 Y_j从而获得 K_ij，
$$\begin{gathered} K_{ij}=Y_j^{X_i}modq \\ =(a^{X_j}{)}^{X_i}modq \\ =a^{X_j{X}_i}modq \end{gathered}$$
用户 $j$用相同的方式获得 K_ij
$$K_{ij}=Y_i^{X_j}modq$$
其他用户必须根据 Y_i 和 Y_j 计算 K_ij ，例如，通过计算
$$K_{ij}=Y_i^{(lo{g}_a{Y}_j)}modq$$
因此，我们看到，如果$logsmodq$ 很容易计算，系统就会崩溃。然而目前我们还没有相反的证据(即如果logs mod q难以计算，则系统是安全的），我们也没有看到任何方法可以在不先获得 X_i或X_j的情况下从Y_i和Y_j计算出K_ij。

​ 如果q是一个稍小于26的质数，那么所有的量都可以表示为b位数。取幂最多需要对q取余2b次乘法模q，而假设循环取对数则需要$q^{1/2}=2^{b/2}$次运算。因此，密码分析者的工作量相对于合法工作量呈指数增长。如果b = 200，则从X_i计算Y_i，或从Y_i和X_j计算Kij，最多需要400次乘法，而==logs mod q则需要2¹⁰⁰次或大约10³⁰次操作。

IV、单向认证

​ 与密钥分发问题相比，身份认证问题可能是在商业交易中普遍采用远程通信的一个更严重的障碍。身份认证是任何涉及合约和记账系统的核心。没有它，商业活动就无法展开。目前的电子认证系统不能满足纯数字的、不可伪造的、依赖于消息的签名需要。它们提供了防止第三方伪造的保护，但不能防止发送方和接收方之间的纠纷。

​ 为了开发一种能够用某种纯粹的电子通信形式代替当前书面合同的系统，我们必须发现一种与书面签名具有相同性质的数字现象。任何人都可以很容易地识别这个签名是真实的，但除了合法签名者之外，任何人都不可能产生它。我们将这种技术称为单向身份认证。由于任何数字信号都可以精确地复制，所以真正的数字签名必须是可识别的。

​ 考虑多用户计算机系统中的“登录”问题。在设置帐户时，用户选择进入系统密码目录的密码。每次登录时，用户都会被再次要求提供密码。通过对所有其他用户保密这个密码，可以防止伪造的登录。然而，这使得保护密码目录的安全性变得至关重要，因为它包含的信息将允许对任何用户进行完美的模拟（登录）。如果系统操作人员有访问目录的合法理由，那么问题就更加复杂了。允许这种合法的访问，但禁止所有其他访问，几乎是不可能的。

​ 这就导致了一个显然不可能实现的要求，即新的登录过程能够在不知道密码的情况下判断密码的真实性。虽然这个要求在逻辑上似乎是不可能的，但却很容易得到满足。当用户首次输入密码 PW 时，计算机会自动、透明地计算一个函数 $f(PW)$并将其存储在密码目录中，而不是将 PW 。每次连续登录时，计算机计算$f(X)$，其中X是提供的密码，并将 $f(X)$ 与t存储值 $f(PW)$ 进行比较。当且仅当它们相等时，用户被认为是真实的。由于函数f每次登录必须计算一次，因此它的计算时间必须很短。100万份指示(按价格计算大约需要0.10美元)似乎是这种计算的合理限度。但是，如果我们能够确保计算$f^{-1}$需要10³⁰或更多的指令，那么那些破坏系统以获取密码目录的人实际上就不能从$f(PW)$获得PW，因此也就不能进行未经授权的登录。注意，登录程序不接受$f(PW)$作为密码字，因为它将自动计算$f(f(PW))$，而$f(f(PW))$与密码目录中的条目$f(PW)$不匹配。

​ 我们假设函数$f$是公共信息，所以计算$f^{-1}$ 的困难性能够知道。这些函数被称为单向函数，最初是由R. M. Needham在登录过程中使用的[9，第91页]。他们在最近的两篇论文[10]，[11]中也讨论了它们，这两篇论文为单向函数的设计提供了有趣的方法。

​ 更确切的讲，如果一个函数 $f$ 是单向函数，那么对于函数定义域内的任意参数$x$ ，很容易计算出$f(x)$的值，然而，对于函数值域内几乎所有的y，从$y=f(x)$中解方程求出相应的$x$，在计算上是不可行的。

​ 值得注意的点是，我们定义的函数从计算的角度来看是不可逆的，但是它的不可逆性与数学中通常遇到的完全不同。通常，当点$y$的逆不唯一时，函数$f$是“不可逆的”，（即：存在不同的点$x_1$ 和 $x_2$，使得$f(x_1)=y=f(x_2)$）。我们强调这不是需要的那种倒置困难。而是，在知道$y$值和$f$的情况下，计算任何具有$f(x)=y$性质的$x$都是极其困难的。在极端情况下，如果$f(x)=y_0$对于定义域内的所有$x$，那么$f^{-1}(y_0)$ 的范围是，我们可以取任意$x$等于$f^{-1}(y_o)$。因此，$f$不能太简并。少量的简并度是可以容忍的，并且，如后面所讨论的，它可能存在于最有前途的单向函数类中。

​ 多项式是单向函数的一个基本例子。求多项式方程$p(x)=y$的根$x_0$要比求多项式$p(x)$在$x=x0$处的值困难得多。Purdy[11]建议在有限域上使用非常高阶的稀疏多项式，这些多项式的解与求值时间之比非常高。第六节较详细地讨论了单向函数的理论基础。如第五节所示，单向函数在实践中很容易设计。

​ 单向函数登录协议只解决了多用户系统中出现的一些问题。它在不使用时保护系统的身份验证数据，但仍然需要用户向系统发送真实的密码。防范窃听必须通过额外的加密来提供，而防范纠纷威胁的措施则完全不存在。

​ 公钥密码系统可以用来产生一个真正的单向认证系统，如下所示。如果用户A希望向用户B发送一条消息M，他将使用他的私钥中“解密”该消息（即：对消息加密），并发送$D_A(M)$。当用户B接收它,他可以读取它,并A用户的公钥$E_A$ "加密"它（即消息进行解密）。B也节省了证明$D_A(M)$来自用户A的应答时间。任何人都可以检查这一主张通过用户A的公钥$E_A$操作$D_A(M)$ 来恢复M，以检查这一真实性 。因为只有与这个属性可以生成一条消息，因此解决单向认证问题的关键是要紧跟公钥密码体制的发展。

​ 单向消息身份认证有一部分解决方案，由马萨诸塞州计算机协会的Leslie Lamport向作者建议。该技术使用一个单向函数$f$ 将k维二进制空间映射到自身，k的阶数为100。如果发送者希望发送一个N位的消息，他将生成2N位，随机选择的k维二进制向量$x_1,X_1,x_2,X_2，.\dots ，x_N,X_N$ 是保密的。给接收方$f$ 下对应的图像，即$y_1,Y_2,y_2,Y_2，\dots ，y_N,Y_N$ 。稍后，当发送消息$m=(m_1+m_2，\dots ，m_N)$ 时，发送者根据$m_1$= 0还是1发送$x_1$ 或 $X_1$ 。他发送$x_2$或$X_2$取决于$m_2$是0还是1，等等。接收方在接收到的第一个块上使用$f$ 进行运算，查看它是否生成$y_1$或$Y_1$作为其图像，从而了解它是$x_1$ 还是$X_1$，以及$m_1$ = 0还是1。以类似的方式，接收方能够确定$m_2,m_3，\dots ，m_N$ 。但接收方没有能力伪造甚至 $1bit$ 的消息。

​ 这只是一部分解决方案，因为需要大约100倍的数据扩展。然而，当N 大约是一兆比特或更多时，有一个修正可以消除扩展问题。设$g$是一个从二进制n维空间到二进制n维空间的单向映射，其中n约等于50。取 N bit信息$m$，用$g$ 对其进行运算，得到一个 n 位的向量 $m^{{}^{\prime }}$。然后使用之前的方案发送$m^{{}^{\prime }}$ 。如果$N=10^6,n=50,k=100$，添加 $kn=5000$的身份验证码到该消息中。因此，在传输过程中只需要$5\%$ 的数据扩展（如果包括 $y_1，Y_1，\dots ，y_N，Y_N$ 的初始交换，则需要$15\%$）。尽管有大量的其他消息（平均约为 $2^{N-n}$）具有相同的身份验证序列，但是$g$ 的单向性使得它们在计算上是不可能被找到，因此无法被伪造。实际上，$g$ 一定比一般的单向函数更强，因为敌手不仅需要有$m^{{}^{\prime }}$，而且还需要有它的一个逆像 $m$。即使给定了$m$，也很难找到它的逆像$m^{{}^{\prime }}$ 。找到这种函数（函数$g$）似乎没什么困难（见第五节）。

​ 下面是单向用户身份认证问题的另一部分解决方案。用户生成密码$X$ 并对其保密。他给出了一个系统$f^T(X)$ ，其中$f$ 是单向函数。在 t 时刻，适当的身份验证器是$f^{T-t}(X)$，系统通过应用公式$f^T(X)$对其进行验证。由于$f$的单向性，过去的响应对于伪造新的响应来说毫无价值。此方案的问题是，合法用户登录可能需要相当数量的计算（尽管跟伪造登录比少很大数量级）。例如，如果 t 每秒钟增加一次，并且系统必须对每个密码工作一个月， 那么t = 260万。然而，用户和系统必须对每次登录进行平均130万次的迭代。虽然这个问题不是不可克服的，但它显然限制了方案的使用。如果有一个计算$f^{（2\uparrow n）}$ 的简单方法，对于$n=1，2，\dots$ ，这个问题就能够被克服，例如 $X^8=((X^2{)}^2{)}^2$ 。因为 $T-t$ 和 $t$ 的二元分解能够加快$f^{T-t}$ 和 $f^t$ 的计算速度。然而，$f^t$ 的快速计算可能会妨碍 $f$ 是单向的。

V、问题的相互关系和陷门

​ 在本节中，我们将展示到目前为止提出的一些密码学问题可以被简化为其他问题，从而根据困难性定义一个大概顺序。我们还将介绍具有陷门的困难问题。

​ 在第二节中，我们展示的旨在保护隐私的密码系统也可用来提供针对第三方伪造的认证。这样的系统也可以被用来创造其他加密对象。

​ 一个能够抵抗已知明文攻击的密码系统可以用来产生单向函数。

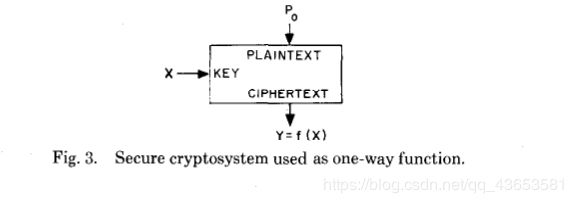
​ 如图3所示，以能抵抗已知明文攻击的密码系统$\{S_K:\{P\}\to \{C\}{\}}_{K\in \{K\}}$ 为例，固定 $P=P_0$ 并考虑映射
$$f:K\to C$$

定义
$$f(X)=S_X(P_0)$$
这个函数是单向的，因为求解给定$f(X)$ 的 $X$ 等价于从单个已知明文对中找到密钥的密码分析问题。公开的$f$ 现在相当于公开的$S_K$ 和 $P_0$。

​ 虽然与这个结果相反的不一定是正确的，但是在搜索单向函数时发现的函数有可能产生良好的密码系统。这实际上是发生在第三节[8]讨论的离散指数函数中。

​ 单向函数是块密码和密钥生成器的基础。密钥生成器是一种伪随机位生成器，它的输出（密钥流）被以二进制形式模2加到一条消息上，模仿“一次一密”。该密钥被用作确认伪随机密钥流序列的“种子”。因此，一种已知明文攻击被简化为从密钥流确定密钥的问题。为了保证系统的安全，从密钥流中计算密钥在计算上是不可行的。然而，为了使系统可用，从密钥计算密钥流必须在计算上很简单。因此，根据定义，一个密钥生成器是一个单向函数。

​ 使用任何一种密码系统作为单向函数都会遇到一个小问题。如上所述，如果函数$f$ 不是唯一可逆的，那么就没有必要（或者不可能）找到所使用的$X$ 的实际值。相反，（找到）任何具有相同图像的$X$ 就满足了。而且，虽然一个密码系统中的$S_K$ 必须是双射的，但是上面所定义的从密钥到密码的函数$f$ 没有这样的限制。实际上，要保证一个密码系统具有这种特性似乎相当困难。一个好的密码系统中，映射$f$被期望拥有随机选择映射的特性（即$f(X_i)$ 是从所有可能的 Y中被随机的选中，并且连续的选择是相互独立的）。这种情况下，如果一致地选择$X$，并且拥有相同数量的密钥和消息($X和Y$) ，那么结果 $Y$ 有 $k-1$个逆的概率大约是$e^{-1}/k!，k\in \{0，1，2，\dots \}$。这是一个均值λ = 1 的泊松分布，移动了一个单位。因此，期望的逆数只有2，。虽然$f$ 可能更简并，但一个好的密码系统因为密钥没有得到很好的利用而不会太简并。在最坏的情况下，如果对于某些$Y_0$ 有 $f(X)\equiv Y_0$，有 $S_k(P_0)=C_0$ ，而$P_0$的加密完全不依赖与密钥。

​ 虽然我们通常对值域和定义域范围相当的函数感兴趣，但也有例外。在前一节中，我们需要一个单向函数将长字符串映射到更短的字符串上。通过使用密钥长度大于块大小的分组密码，可以使用上述方案获得这些功能。

​ Evans等人对从块密码构造单向函数的问题有一种不同的方法。不是选择一个固定的$P_0$作为输入，而是使用函数
$$f(X)=S_X(X)$$
这是一种很有吸引力的方法，因为这种形式的方程通常很难求解，即使$S$ 族相对简单。然而，这种增加的复杂度破坏了系统 $S$ 在已知明文攻击下的安全性与$f$ 的单向性之间的等价性。

​ 第四节已经说明了另一种关系。

​ 公钥秘密系统可用于生成单向认证系统。

​ 相反的情况似乎并不成立，这使得公钥密码系统的构造成为一个比单向身份认证更加困难的问题。类似地，公钥秘密系统可以用作公钥分发系统，反之则不成立。

​ 由于公钥密码系统中被使用的$E$ 和 $D$ 必须是公共的，$E$ 指定了将输入消息转换为输出密码的完整算法。由于这样的公钥系统实际上是一个单向陷门函数，这些函数并不是真正意义上单向的，因为存在简单的逆运算。但通过正演函数，寻找一个简单逆运算的算法在计算上是不可行的。只有通过了解特定的陷门信息（例如，生成 $E-D$ 对的随机比特串），才能很容易地找到易于计算的逆运算。

​ 在前一段中已经见到了陷门的形式，即单向陷门函数，但它还存在其他的变体。陷门密码具有强烈抵抗密码设计中没有掌握陷门信息的人进行密码分析的能力。这使得设计者可以将系统卖给客户后破坏系统，同时还可以保住自己作为安全系统构建者的声誉。值得注意的是，并不是更聪明或更精通密码学才能让设计者做别人做不到的事情。如果他失去了陷门信息，他也不会比任何人做得更好。这种情况正好类似于密码锁。任何指导这个组合的人都能在几秒钟内完成一个熟练的锁匠几个小时才能完成的工作。然而，如果他忘记了组合方式，他就没有优势了。

​ 一个门限密码系统可用用来产生一个公钥分发系统。

​ $A$ 和 $B$ 为了建立一个公共的私钥，$A$ 选择一个随机的$key$，发送一个任意的明-密文对给$B$ 。$B$ ，将陷门密码公之于众，但是对陷门信息保密，使用明-密文对求解这个$key$ 。现在 $A$ 和 $B$ 有了一个共同的密钥。

​ 目前几乎没有证据表明陷门密码的存在。然而，这是一个独特的可能性，当从一个可能的敌手中接收到一个密码系统时应该记住这种可能性[12]。

​ 根据定义，我们要求陷门问题是这样一个问题：设计陷门在计算上是可行的。这就为第三种类型的实体留下了空间，我们将使用前缀“quasi（准）”。例如，一个"quasi（准）"单向函数不是单向的，因为它存在一个易于计算的逆运算。然而，即使对于设计者来说，找到易于计算的逆运算在计算上是不可行的。因此，一个“quasi（准）"单向函数可以替代单向函数，基本上是不会造成安全性损失。

​ 将陷门信息丢给一个单向陷门函数将使其成为“quasi（拟）"单向函数，但也可能存在无法通过这种方式获得的单向函数。

​ 准单向函数被排除在单向函数之外，这完全是一个定义问题。我们可以在广义或者狭义上讨论单向函数。

​ 类似地，“quasi(准)”安全密码是一种能成功抵抗即使是设计者进行密码分析的密码，但对于这种密码，存在一种计算效率高的密码分析方法（当然，这种算法在计算上是不可行的）。同样，从实用的角度来看，安全密码和“quasi（准）”安全密码之间本质上没有区别。

​ 我们已经看到，公钥密码系统隐含了单向陷门函数的存在。然而，反之则不正确。要使单向陷门密码作为公钥密码系统使用，它必须是可逆的（即，有唯一的逆）。

VI、计算复杂度

​ 密码学不同于所有其他领域，努力会导致它的要求可能被满足。简单的转换将把易读的文本转换成看起来毫无意义的混乱值。批评者希望声明，密码分析仍可能恢复其（即：混乱值）意义，但如果他要证明自己的观点是正确的，那么他将面临一场艰难的论证。然而，经验表明，很少有系统能够抵御熟练的密码分析者的协同攻击，许多被认为是安全的系统随后被破坏。

​ 因此，判断新系统的价值一直是密码学家关注的中心问题。在16世纪和17世纪，数学参数经常被用来论证密码方案的强度，通常依赖计数方法来显示可能的密钥的天文数字。虽然这个问题很难用如此简单的方法解决，但即使是著名的代数家卡丹诺也落入了这个陷阱[2,p.145]。当那些曾被如此论证过的系统的强度一再被打破时，为系统的本质提供数学证明的概念就声名狼藉了，取而代之的是密码分析攻击的证明。

​ 然而，在本世纪，钟摆已开始向另一个方向摆动。在一篇与信息理论的诞生密切相关的论文中，香农[3]指出，自20年代后期就开始使用的“一次一密”系统提供了“完全保密性”(一种无条件安全的形式)。香农研究的可证明安全的系统依赖于密钥的使用，密钥的长度随消息的长度线性增长，或者依赖于完美的源代码编码，因此对于大多数用途来说太笨拙了。我们注意到，无论是公钥密码系统还是单向身份认证系统，都不可能是无条件安全的，因为公共信息总是在有限集合的成员中唯一地决定秘密信息。由于计算量不受限制，因此这个问题可以通过简单的搜索来解决。

​ 在过去的十年里，出现了两个密切相关的专门研究计算成本的学科:计算复杂性理论和算法分析。前者将计算中已知的问题按难度分成大类，而后者则专注于寻找更好的算法并研究它们所消耗的资源。在简单介绍复杂性理论之后，我们将探讨复杂性理论在密码学中的应用，特别是对单向函数的分析。

​ 如果一个函数可以由一个确定性的图灵机在一个时间内计算出来，而这个时间的上界是一个关于其输入长度的多项式函数，那么这个函数就属于复杂性$P$类(多项式)。有人可能认为这是一类易于计算的函数，但更准确的说法是，对于至少一些输入，不属于此类的函数一定很难计算。有些问题是已知不属于$P$类[13,pp. 405-425]的。

​ 工程中出现的许多问题，用任何已知的技术都无法在多项式时间内解决，除非它们是在具有无限并行度的计算机上运行。这些问题可能属于也可能不属于$P$类，但是属于$NP$类(对于不确定的多项式)，即在“不确定的”计算机上，可以在多项式时间内解决的问题（即：一个具有无限并行度的数)。显然，$NP$类包括$P$类，复杂性理论中一个重要的开放问题是$NP$类是否严格地更大。

​ 已知$NP$时间可解而$P$时间内不可解的问题包括旅行商问题、命题演算的可满足性问题、背包问题、图着色问题以及许多调度和最小化问题[13,pp. 363-404]，[14]。我们看到，并不是缺乏兴趣或努力使人们无法及时找到解决这些问题的方法。因此，人们坚定地认为，这些问题中至少有一个不属于$P$类，因此，严格地说，$NP$类更大。

​ Karp 已经确定了$NP$问题的一个子类，称为$NP$完全问题，它的性质是，如果其中任何一个问题在$P$中，那么所有的$NP$问题都在$P$中。

​ 虽然$NP$完全问题显示出在密码学上的应用前景，但目前对其困难的理解只包括最坏的情况分析。出于加密的目的，必须考虑典型的计算成本。然而，如果我们用平均或典型计算时间来代替最坏情况的计算时间作为复杂度的度量，那么当前$NP$完全问题等价性的证明就不再有效。这为研究提出了几个有趣的课题。信息理论家熟悉的集合和典型性概念有明显的作用。

​ 我们现在可以在所有的计算问题中确定一般密码分析问题的位置。

​ 对于一个可以在$P$时间内完成加密和解密操作的系统，其密码分析难度不能大于$NP$。

​ 要了解这一点，可以观察到，任何密码分析问题都可以通过从有限集中选择一个密钥、反像等来解决。非确定性地选择密钥，并在$P$时间内验证它是否是正确的。如果有M个可能的键可供选择，则必须使用M倍并行性。例如，在已知明文攻击下，明文在每个密钥下同时加密，并与密码进行比较。从理论上讲，加密只需要$P$个时间，而密码分析只需要$NP$个时间。

​ 我们还观察到一般的密码分析问题是$NP$完全问题。这是从我们对密码学问题定义的广度得出的结论。下面讨论一个具有$NP$完全逆的单向函数。

​ 通过研究$NP$完全问题适应于密码使用的方式，密码学可以直接从$NP$复杂性理论中得出结论。特别地，有一个$NP$完全问题称为背包问题，它很容易构造一个单向函数。

​ 设 $y=f(x)=a\cdot x$，其中 $a$ 是一个已知的$n$个整数（$a_1，a_2，\dots ，a_n$）组成的向量，$x$是一个二进制的 n-向量。$y$ 的计算很简单，涉及到最多$n$ 个整数求和。求$f$ 的逆问题被称为背包问题，需要找到$a_i$ 的子集，这个子集的和是$y$。

​ 对所有 $2^n$ 个子集的穷举搜索都呈指数增长，对于$n$大于100或更多的子集，这种搜索在计算上是不可行的。但是，在选择问题的参数时必须谨慎，以确保不存在快捷方式。例如，如果n = 100，每个$a_i$长度为32位，$y$最多为39位，$f$高度退化；平均只需要$2^{38}$ 次就能找到解决方案。更简单一点，如果$a_i=2^{i-1}$，那么求$f$的逆等价于求$y$的二进制分解。

​ 这个例子显示了当代复杂性理论的巨大前景和巨大的缺陷。这个理论只告诉我们，在最坏的情况下，背包问题可能是困难的。没有迹象表明它的困难，为任何特定的阵列。然而，从$\{0，1，2，\dots ，2^{n-1}\}$中一致地选择$\{a_i\}$会导致一个概率为$n\to \infty$ 的难题。

​ 另一个可能的单向函数，在算法分析中很有趣，它是取幂 $modq$，这是由斯坦福大学的John Gill教授向作者建议的。这个函数的单向性已经在第三节中讨论过了。

VII、历史展望

​ 虽然本文中所提出的公钥系统和单向身份认证系统最初似乎并没有受到过去密码技术发展的影响，但我们可以将它们视为数百年前密码技术发展趋势的自然产物。 保密是密码学的核心。然而，在早期的密码学中，人们对什么应该保密存在困惑。凯撒密码(Caesar cipher），其中每个字母都被后面三个位置的字母所取代，因此A被带到D, B到E，等等)等密码系统的安全依赖于对整个加密过程的保密。电报发明之后[2，第191页]，普通系统和特定密钥之间的区别使得普通系统可以被破坏，例如通过盗窃密码设备，而不影响将来用新密钥加密的信息。这一原则由Kerchoffs[2, p. 235]编纂而成，他在1881年写道，密码系统的破坏应该不会给通信者带来不便。大约在1960年，密码系统投入使用，被认为足以抵抗已知的明文密码分析攻击，从而消除了对旧消息保密的负担。每一项进展都减少了该系统中必须保护公众不被公众所知的部分，从而消除了诸如在外交文件公布前改写其内容等繁琐的权宜之计。公钥系统是这种保密性下降趋势的自然延续。

​ 在本世纪之前，密码系统仅限于手工计算或使用简单的类似滑动规则的设备进行计算。第一次世界大战结束后不久，出现了一种革命的趋势，现在这种趋势正在实现。开发了专门用于加密的机器。然而，在通用数字硬件的发展之前，密码学仅限于可以用简单的机电系统进行的操作。数字计算机的发展使它摆脱了使用齿轮计算的限制，并允许根据纯粹的密码标准寻找更好的加密方法。

​ 通过数学证明来证明密码系统的可靠性的无数失败的尝试，导致了上个世纪Kerchoffs提出的通过密码分析攻击进行认证的范例[2,p. 234]。虽然已经制定了一些通用规则，以帮助设计者避免明显的弱点，但最终的测试是由熟练的密码分析人员在最有利的条件下对系统进行攻击(例如，选择明文攻击)。计算机的发展第一次导致了一种算法的数学理论，它可以开始处理估计破坏密码系统的计算难度的难题。因此，数学证明的地位可能会周而复始，重新确立为最好的证明方法。

​ 我们在密码学史上注意到的最后一个特点是业余和专业密码学家的区分。产生密码分析技术一直是专业人员的强项，但创新，尤其是新型密码系统的设计，主要来自业余爱好者。托马斯·杰佛逊（Thomas Jefferson），一位密码业余爱好者，发明了一个在二战中仍在使用的系统，而二十世纪最著名的密码系统——转子机，是由四个完全业余的人同时发明的。我们希望这将激励其他人在这一引人入胜的领域工作，在这一领域，过去几乎完全由政府垄断而不鼓励参与。

参考文献

[1] R. Merkle, “Secure communication over an insecure channel,” submitted to Communications of the ACM.
[2] D. Kahn, The Codebreakers, The Story of Secret Writing. New York: Macmillan,  1967. 
[3] C. E. Shannon, “Communication  theory of secrecy systems,” Bell Syst. Tech. J., vol. 28, pp. 656-715, Oct. 1949. 
[4] M. E. Hellman, “An extension of the Shannon theory approach to cryptography,” submitted to IEEE Trans. Inform. Theory, Sept. 1975.
[5] W. Diffie and M. E. Hellman, “Multiuser cryptographic techniques,” presented at National Computer Conference, New York, June 7-10, 1976.
[6] D. Knuth, The Art of Computer Programming, Vol. 2, Semi- Numerical Algorithms. Reading, MA.: Addison-Wesley, 1969.
[7] --, The Art of Computer Programming, Vol. 3, Sorting and Searching. Reading, MA.: Addison-Wesley, 1973.
[8] S. Pohlig and M. E. Hellman, “An improved algorithm for computing algorithms in GF(p) and its cryptographic significance,” submitted to IEEE Trans. Inform. Theory.
[9] M. V. Wilkes, Time-Sharing Computer Systems. New York: Elsevier, 1972.
[10] A. Evans, Jr., W. Kantrowitz, and E. Weiss, “A user authentication system not requiring secrecy in the computer,” Communications of the ACM, vol. 17, pp. 437-442, Aug. 1974.
[11] G. B. Purdy, “A high security log-in procedure,” Communications of the ACM, vol. 17, pp. 442-445, Aug. 1974
[12] W. Diffie and M. E. Hellman, “Cryptanalysis of the NBS data en- cryption standard” submitted to Computer, May 1976.
[13] A. V. Aho, J. E. Hopcroft, and J. D. Ullman, The Design and Analysis of Computer Algorithms. Reading, MA.: Addison- Wesley, 1974.
[14] R. M, Karp, “Reducibility among combinatorial problems,” in Complexity of Computer Computations. R. E. Miller and J. W. Thatcher, Eds. New York: Plenum, 1972, pp. 855104.