LTE学习-PSS主同步信号
以下内容来自sharetechnote
LTE学习
- PSS主同步信号
- PSS的生成算法
- 不同PSS之间的互相关
- PSS与其相移后的互相关
- PSS与其叠加噪声后的互相关
- SSS次同步信号
- SSS的生成算法
- Zadoff Chu序列
PSS主同步信号
PSS是一种特殊的物理层信号,用于无线帧同步。它的特性如下:
1.映射到72个有源子载波(6个RBs),在FDD模式下,处于slot 0 (Subframe 0)和slot 10 (Subframe 5)中,以直流子载波为中心。
2.在TDD模式下,处于slot 2 (Subframe 2)和slot 12 (Subframe 6)中,以直流子载波为中心。
3.由62个ZC(Zadoff Chu)序列值组成
4.用于下行帧同步
5.决定物理小区ID的关键之一
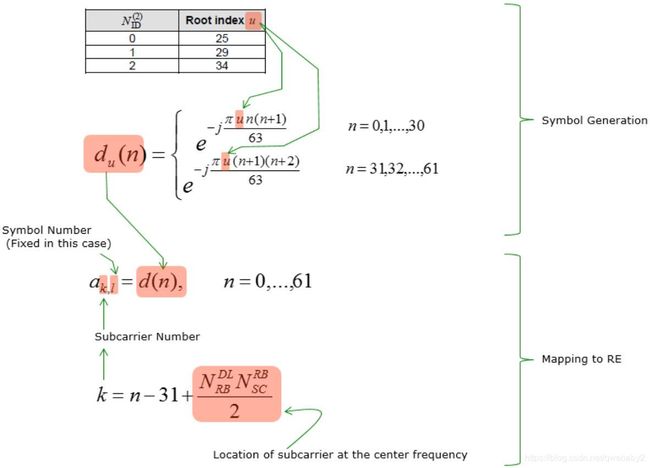
PSS的生成算法
clear all;
u_shift = [25 29 34];
NID = 0;
d_u = [];
for n = 0:61
u = u_shift(NID+1);
if n <= 30
d = exp(-j*pi*u*n*(n+1)/63);
else
d = exp(-j*pi*u*(n+1)*(n+2)/63);
end;
d_u = [d_u d];
end;
subplot(1,3,1);
plot(real(d_u(1:31)),imag(d_u(1:31)),'ko','MarkerFaceColor',[0 0 0]);
axis([-1.5 1.5 -1.5 1.5]);
title('n=0..30');
subplot(1,3,2);
plot(real(d_u(32:62)),imag(d_u(32:62)),'bo','MarkerFaceColor',[0 0 1]);
axis([-1.5 1.5 -1.5 1.5]);
title('n=31..61');
subplot(1,3,3);
plot(real(d_u(1:62)),imag(d_u(1:62)),'ro','MarkerFaceColor',[1 0 0]);
axis([-1.5 1.5 -1.5 1.5]);
title('n=0..61');

从星座图可以看出,PSS是一个ZC序列,由62个符号组成。NCellID不同时,PSS序列也是不同的,这表示PSS序列随NCellID (PCI: Physical CellID)变化而变化。
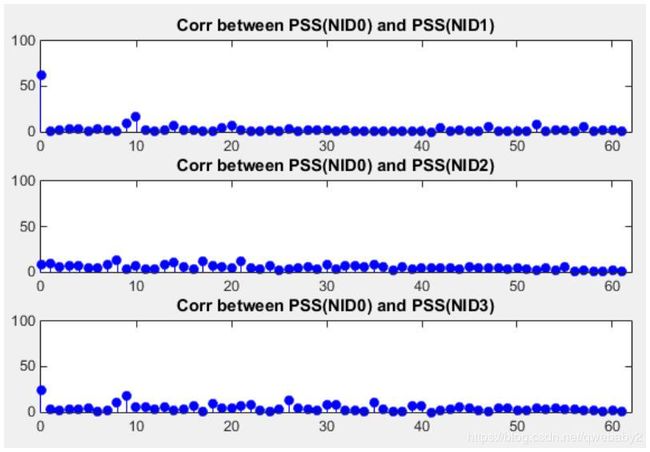
不同PSS之间的互相关
PSS与其相移后的互相关
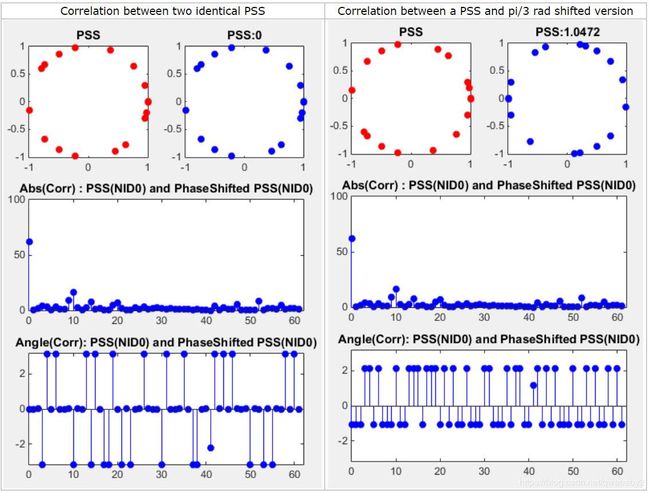
这个例子显示了一个PSS和它发生相移后的互相关性。如下图,即使进行相移,相关性的大小(绝对值)也不会改变。但是可以通过相关角来计算相移的程度。
利用这个特点,就可以在接收信号中识别PSS,而无需担心信道可能发生的相位偏移。此外,还可以通过获取角度的互相关并使用该值补偿(撤消)因信道条件发生的相移。
PSS与其叠加噪声后的互相关
这个例子展示了PSS的噪声容忍度。左边的例子展示了PSS与50dB的信噪比条件下(几乎没有噪声)的相关性,右边的例子展示了PSS与10dB信噪比条件下的相关性。
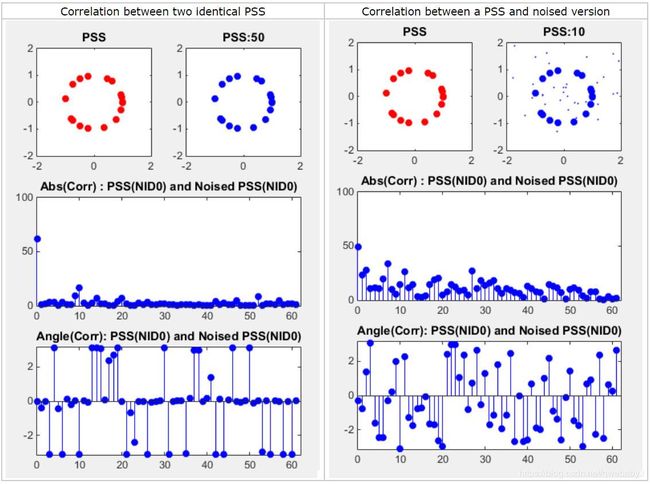
如图,当信道条件较差时,PSS与其叠加噪声后的互相关明显增大。
SSS次同步信号
SSS同PSS一样,是一种特殊的物理层信号,也用于无线电帧同步。它的特性如下:
1.映射到72个有源子载波(6个RBs),在FDD模式下,处于slot 0 (Subframe 0)和slot 10 (Subframe 5)中,以直流子载波为中心。Subframe0中的SSS序列与Subframe5中的SSS序列是不同的。
2.由62个置乱序列组成(基于m序列),奇数索引的元素和偶数索引元素的值是由不同的方程产生的。
3.用于下行帧同步
4.决定物理小区ID的关键之一
SSS的生成算法
Zadoff Chu序列
ZC序列可以用作LTE底层的实现,生成公式:
x q ( m ) = e − j π q m ( m + 1 ) N Z C R S , 0 ≤ m ≤ N Z C R S − 1 x_q(m)=e^{-j \frac{\pi q m (m+1)}{N_{ZC}^{RS} } },0\le m \le N_{ZC}^{RS} -1 xq(m)=e−jNZCRSπqm(m+1),0≤m≤NZCRS−1
其特性如下:
i)序列振幅恒定。从公式可以看出,它是 e − j e^{-j} e−j的形式,转换成欧拉形式后,会得到 e − j = c o s ( ) − j s i n ( ) e^{-j}=cos()-jsin() e−j=cos()−jsin(),这是一个由实数和虚数组成的复数。如果把ZC序列画在星座图上,所有的点都在一个圆上,而这意味着这些序列的振幅是恒定的。如下图,二、三列是ZC序列的一个实例。第二列是实部,第三列是虚部。
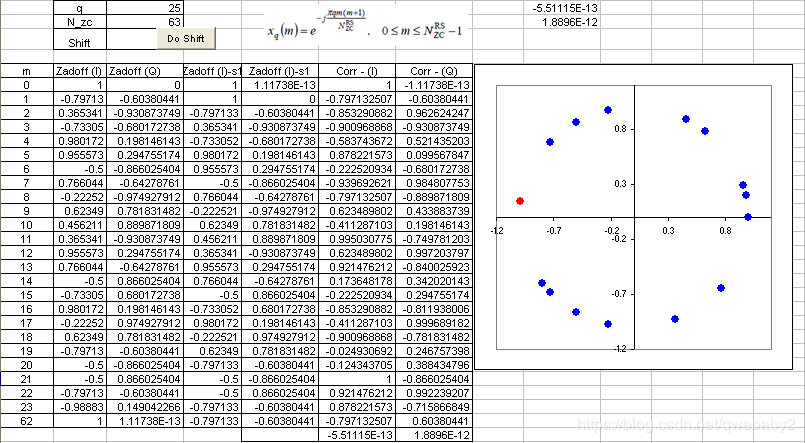
ii)零自相关。如果用上面给出的公式创建一个序列,然后通过偏移N来得到另一个序列(N可以是1,2,…,序列大小-1)。那么这两个序列的相关性是0。以上图的电子表格为例,第二列、第三列是由公式创建的序列。而第四列、第五列是由第三列、第四列偏移得来。在最下面的两个单元格可以看到两组序列的相关性,几乎为0,即这两个序列是正交的。这说明可以通过移动ZC序列来创建许多正交序列,十分方便,而在无线通信中创建正交序列极其重要。
任何具有上述两个特性的序列称为CAZAC序列(恒幅零自相关波形)。
iii)两个ZC序列的互相关为 1 / N z c 1/\sqrt{N_{zc}} 1/Nzc。如果使用电子表格中显示的公式创建两个序列,只需更改q(q应该是质数),并计算两个序列的相关性,结果将是 1 / N z c 1/\sqrt{N_{zc}} 1/Nzc。
在LTE中,除了PSS由ZC序列组成,还有以下部分也用到ZC序列:
i) random access preamble (PRACH)
ii) PUCCH DMRS
iii) PUSCH DMRS
iv) sounding reference signals(SRS)