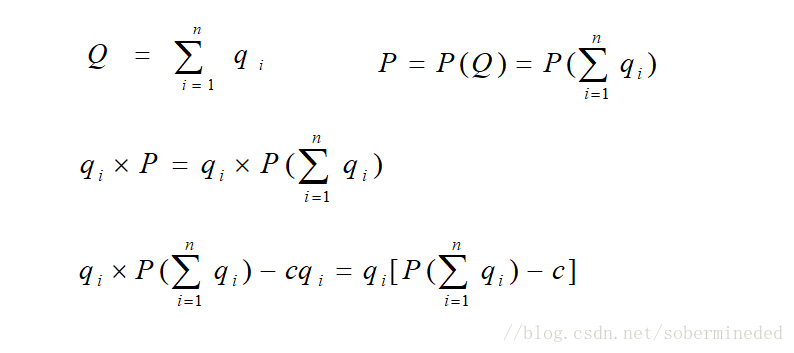1.2 几个经典博弈模型(囚徒的困境、赌胜博弈、产量决策的古诺模型)
1.2.1 囚徒的困境
一、基本模型
囚徒的困境是图克(Tucker)1950年提出的。
该博弈是博弈论最经典、著名的博弈。该博弈本身讲的是一个法律刑侦或犯罪学方面的问题,但可以扩展到许多经济问题,以及各种社会问题,可以揭示市场经济的根本缺陷。
假设囚徒2选择不坦白,囚徒1选择坦白的收益(0) > 选择不坦白的收益(-1),所以囚徒1选择坦白。
(根据个体理性的原则,囚徒1根据自身利益最大的原则行事,不会关心此时另一方会被重判8年的问题)
假设囚徒2选择坦白,囚徒1选择坦白的收益(-5) > 选择不坦白的收益(-8),所以囚徒1仍然选择坦白。
也就是说,无论囚徒2选择坦白还是不坦白,囚徒1都会选择坦白。“坦白”是囚徒1的一个“上策”。
同理可以分析:
假设囚徒1选择不坦白,囚徒2选择坦白的收益(0) > 选择不坦白的收益(-1),所以囚徒2选择坦白。
假设囚徒1选择坦白,囚徒2选择坦白的收益(-5) > 选择不坦白的收益(-8),所以囚徒2仍然选择坦白。
也就是说,无论囚徒1选择坦白还是不坦白,囚徒2也都会选择坦白。“坦白”也是囚徒2的一个“上策”。
所以该博弈的最终结果必然是囚徒1和囚徒2都选择坦白。
在市场竞争方面典型的囚徒的困境现象之一是寡头之间的价格战。
和囚徒的困境博弈完全相似:
假设寡头2选择高价,寡头1选择低价的收益(150) > 选择高价的收益(100),所以寡头1选择低价。
假设寡头2选择低价,寡头1选择低价的收益(70) > 选择高价的收益(20),所以寡头1仍然选择低价。
也就是说,无论寡头2选择高价还是低价,寡头1都会选择低价。“低价”是寡头1的一个“上策”。
同理可以分析:
假设寡头1选择高价,寡头2选择低价的收益(150) > 选择高价的收益(100),所以寡头2选择低价。
假设寡头1选择低价,寡头2选择低价的收益(70) > 选择高价的收益(20),所以寡头2仍然选择低价。
也就是说,无论寡头1选择高价还是低价,寡头2都会选择低价。“低价”也是寡头2的一个“上策”。
1.2.2 赌胜博弈
赌博、竞技等构成的博弈问题,在经济中也有许多应用,赌胜博弈也是一类重要的博弈问题,对经济竞争和合作也有很大启示。
赌胜博弈的特点是一方得等于另一方失,不可能双赢,属于“零和博弈”。
一、田忌赛马
- 该博弈中有两个博弈方即齐威王和田忌
- 两博弈方可选择的策略是己方马的出场次序,因为三匹马的排列次序共有3!=3*2=6种,因此双方各有6种可选择的策略
- 双方在决策前都不能预先知道对方的决策,因此可以看做是同时选择策略的,决策没有先后次序关系
- 如果把赢一千斤铜记成得益1,输一千斤铜记成得益-1,则两博弈方在双方各种策略的组合下的得益矩阵如下:
取胜关键:不让对方猜到自己策略,尽可能猜出对方策略
二、猜硬币博弈
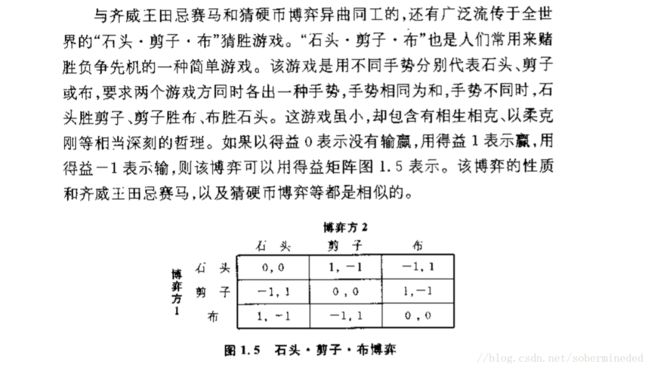
三、石头、剪子、布
1.2.3 产量决策的古诺模型
古诺模型是寡头产量竞争,是市场经济中最常见的问题之一。
古诺1838年提出,直到现在还是经常使用。
古诺模型有很多扩展。
古诺模型与囚徒困境相似,对理解市场经济和博弈分析本身都有重要价值。
一、三厂商离散产量
二、n个厂商连续产量博弈
该博弈中各博弈方的可选策略数都是无穷大,意味着我们不可能用罗列的办法或者矩阵、图表的形式把它们表达出来。
总结上面几个式子为:
因此,厂商i的产量决策与其他厂商的产量决策之间是复杂的相互依存关系。
其实,如果把上一个三厂商离散变量的模型改为连续产量的,就是现在这个模型的一个具体的例子。