机器学习3:K近邻法K-Nearest-Neighbor Classifier/KNN(基于R language&Python)
k k k 近邻法是一种基本分类与回归问题。 k k k 近邻法的输入为实例的特征向量,对应于特征空间中的点;输出为实例的类别,可以取很多类。 k k k 近邻法假设给定一个训练数据集,其中的实例类别已定。分类时,对新的实例,根据其 k k k 个最近邻的训练实例的类别,通过多数表决等方式进行预测。因此, k k k 近邻法不具有显式的学习过程。 k k k 近邻法实际上利用训练数据集对特征向量空间进行划分,并作为其分类的“模型”。 k k k 近邻法的三个要素是: k k k 值的选择、距离度量及分类决策规则1。
K近邻法
- 基本原理方法
- k k k 近邻法概述
- 定量变量标准化
- 距离度量
- 定量变量的距离度量
- 定性变量的距离度量
- 缺失值的距离度量
- k k k 值的选择
- 分类决策规则
- KNN分类问题
- 多数表决规则
- 加距离权重的多数表决规则(博主绞尽脑汁搞懂了核函数加权法)
- KNN回归问题
- k k k 近邻法特点
- 优点
- 缺点
- k k k 近邻法评估
- 手算例子
- 代码:R语言
- 分类问题:投票无加权+自变量为定量变量
- 分类问题:投票有加权+自变量为定量变量(手算问题核验)
- 回归问题:有加权+训练集为混合性数据
- 回归问题:有加权+训练集为混合性数据+含缺失数据
- 代码:Python
- sklearn库的KNeighborsClassifier函数简介
- 分类问题:定量变量的情况
- 等权重
- 按距离加权
- 分类问题:定性变量的情况
- 独热编码
- Iris数据调参案例
- Iris数据画分类效果图案例
- 参考资料
基本原理方法
k k k 近邻法概述
k k k 近邻法的算法如下:
输入:训练集 D = { ( x i , y i ) } i = 1 N D=\{(x_i,y_i)\}_{i=1}^N D={(xi,yi)}i=1N ,其中 x i x_i xi 为实例的特征向量, y i y_i yi 为实例的类别
输出:实例 x x x 所属的类别 y y y
(1)根据给定的距离度量,在训练集 D D D 中找出与 x x x 最近邻的 k k k 个点,涵盖这 k k k 个点的 x x x 的邻域称为 N k ( x ) N_k(x) Nk(x);
(2)在 N k ( x ) N_k(x) Nk(x) 中根据分类决策规则(如多数表决)决定 x x x 的类别 y y y: y = a r g m a x c j ∑ x i ∈ N k ( x ) I ( y i = c j ) , i = 1 , 2 , ⋯ , N ; j = 1 , 2 , ⋯ , K y=argmax_{c_j}\sum_{x_i\in N_k(x)} I(y_i=c_j),i=1,2,\cdots,N;j=1,2,\cdots,K y=argmaxcj∑xi∈Nk(x)I(yi=cj),i=1,2,⋯,N;j=1,2,⋯,K,即有 K K K 种类别。
k k k 近邻法是一种惰性学习算法,它存储训练集实例但并没有立刻进行建模,直到获得测试集,必须对其进行分类为止才开始进行建模。
懒惰学习算法:只存储训练数据(或仅进行少量处理)但并不马上进行建模,等到给出测试集才开始建模。
与之相反地,
积极学习算法:给定训练集就立马进行建模,再接收新的测试数据在建立好的模型上进行预测。
| 懒惰学习算法与积极学习算法的比较 | |
|---|---|
| 时间成本 | 懒惰学习算法训练花的时间更少,但预测花的时间更多 |
| 准确率 | 惰性学习算法有效地使用了更丰富的假设空间,因为它使用了许多局部线性函数来形成对目标函数的隐式全局近似;积极学习算法则必须遵循涵盖整个实例空间的一个单一假设 |
除了 k k k 近邻法之外,典型的惰性学习算法还有局部加权回归、构造局部近似、基于案例的推理和使用符号表示和基于知识的推理。
KNN算法需要有四个步骤:
- 定量变量标准化
- 距离度量
- 定义邻居个数 k k k
- 预测
- 分类问题:多数投票 Majority Vote
- 回归问题:把邻居的取值平均 Averaging
定量变量标准化
由于计算距离时,会涉及到将变量所有维度相加的计算,故需要对每个变量进行标准化。否则,因为尺度不同的原因,尺度比较大的变量比尺度比较小的变量会有更大的影响。
在叙述具体怎么做标准化之前,有一个重中之重的提醒:训练集标准化完了以后,测试集的标准化是要利用训练集标准化的“工具”来进行的!例如中心标准化,测试集标准化必须用训练集数据的均值和标准差,这是因为在建好模型预测之前是不可以动用测试集的信息的,一切信息只能来源于训练集。
标准化方法主要有两种,一种是 m i n − m a x min-max min−max 归一化(归一化后数据被缩放到 [ 0 , 1 ] [0,1] [0,1] 范围内):
x n o r m a l i z a t i o n = x − m i n ( x ) m a x ( x ) − m i n ( x ) x_{normalization}=\frac{x-min(x)}{max(x)-min(x)} xnormalization=max(x)−min(x)x−min(x)
另一种是 z − s c o r e z-score z−score 标准化:
x s t a n d a r d i z a t i o n = x − m e a n ( x ) s t d ( x ) x_{standardization}=\frac{x-mean(x)}{std(x)} xstandardization=std(x)x−mean(x)
距离度量
定量变量的距离度量
特种空间中两个实例点的距离是两个实例点相似程度的反映。 k k k 近邻模型的特征空间一般是 n n n 维实数向量空间 R n \textbf{R}^n Rn,使用的是欧式距离。一般地,有两种距离度量方式:欧式距离和闵氏距离。
特征空间中两点的欧式距离为:
d ( x i , x j ) = ∑ l = 1 m ( x i ( l ) − x j ( l ) ) 2 d(x_i,x_j)=\sqrt{\sum_{l=1}^m (x_i^{(l)}-x_j^{(l)})^2} d(xi,xj)=l=1∑m(xi(l)−xj(l))2
其中 x i = ( x i 1 , x i 2 , ⋯ , x i m ) x_i=(x_i^{1},x_i^{2},\cdots,x_i^{m}) xi=(xi1,xi2,⋯,xim);
特征空间中两点的曼哈顿距离为:
d ( x i , x j ) = ∑ l = 1 m ∣ x i ( l ) − x j ( l ) ∣ d(x_i,x_j)=\sum_{l=1}^m \mid x_i^{(l)}-x_j^{(l)} \mid d(xi,xj)=l=1∑m∣xi(l)−xj(l)∣
特征空间中两点的闵氏距离为:
d ( x i , x j ) = ( ∑ l = 1 m ∣ x i ( l ) − x j ( l ) ∣ p ) 1 p d(x_i,x_j)=(\sum_{l=1}^m \mid x_i^{(l)}-x_j^{(l)} \mid ^p)^{\frac{1}{p}} d(xi,xj)=(l=1∑m∣xi(l)−xj(l)∣p)p1
以下图为例,绿色的直线代表两点之间的欧式距离,而红色和黄色的线为两点的曼哈顿距离。感受一下两者的不同2:
定性变量的距离度量
定性变量就是属于同一类别的亮点距离为0,属于不同类别的两点距离为1(0-1距离)。
举例说明定性变量的距离度量,X={red},Y={red},Z={blue},d(X,Y)=0,d(X,Z)=1。
缺失值的距离度量
定性变量在0-1距离度量下,取值若为缺失值的点的距离定义:
| x1 | x2 | 距离 |
|---|---|---|
| 缺失值 | - | 1 |
| - | 缺失值 | 1 |
| 缺失值 | 缺失值 | 1 |
定量变量在0-1正则化后,取值若为缺失值的点的距离定义:
| x1 | x2 | 距离 |
|---|---|---|
| 缺失值 | - | max(x2,1-x2) |
| - | 缺失值 | max(x1,1-x1) |
| 缺失值 | 缺失值 | 1 |
k k k 值的选择
k k k 值的选择会对 k k k 近邻法的结果产生重大影响。
如果选择较小的 k k k 值,即用较小的邻域中的训练集实例进行预测。会导致学习的近似误差(bias)减小——只有与输入实例较近的(相似的训练实例)才会对预测结果起作用;但缺点是学习的估计误差(variance)会增大——预测结果会对近邻的实例点非常敏感:只要变换一下训练集中的实例,邻居实例就会变化很大,从而导致预测结果变化很大。
换句话说, k k k 值的减少就意味着整体模型变得复杂,容易发生过拟合。
如果选择较大的 k k k 值,即用较大的邻域中的训练集实例进行预测。其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大。这时与输入实例较远的(不相似的)训练实例也会对预测起作用,是预测发生错误。
换句话说, k k k 值的增大就意味着整体模型变得简单。
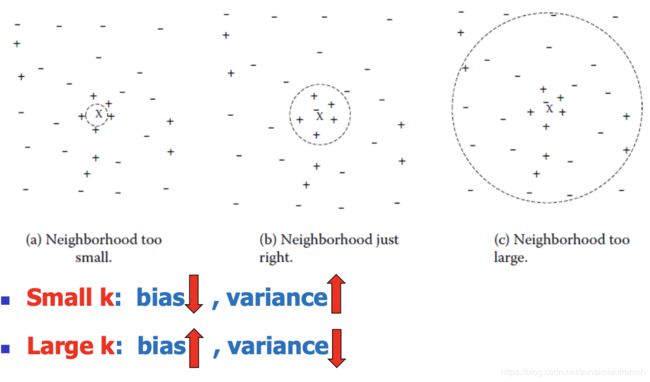
在应用中, k k k 值一般取取 3~10 或取 n 训 练 集 \sqrt{n_{训练集}} n训练集,通常采用交叉验证法来选取最优的 k k k 值。下图展示了训练集、测试集、十折交叉验证及贝叶斯四者的错判率随 k k k 值的变化。
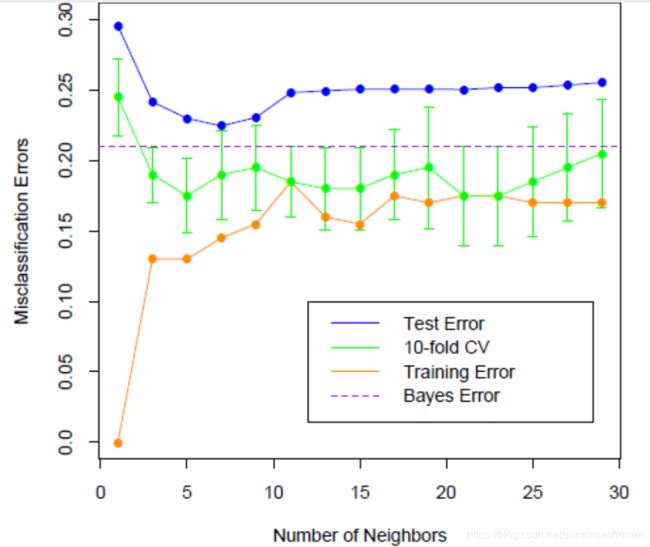
显然, k = 0 k=0 k=0 时,训练集错判率为0。根据上图,我们可以发现随着 k k k 值的增长,训练集错判率逐步上升然后逐渐平稳,测试集错判率逐步下降然后逐渐平稳,理想的 k k k 值的选取应当让训练集和测试集错判率都比较低并处于稳定值。十折交叉验证的绿色上下标示意味着,在该错判率上下一个标准误差。
分类决策规则
KNN分类问题
多数表决规则
k k k 近邻法中的分类决策规则往往是多数表决规则(majority voting rule),即由输入实例/测试集实例的 k k k 个近邻的训练实例德维尔多数类决定输入实例的类。我们不妨用公式来表达这种准则,测试集中点 z z z 的类别 c z c_z cz 可以用多数表决准则得到:
c l a s s ( z ) = arg max c l a s s ( z ) = c j ∑ x i ∈ N k ( z ) I ( y i = c j ) class(z)=\mathop{\arg\max}_{class(z)=c_j} \sum_{x_i\in N_k(z)}I(y_i=c_j) class(z)=argmaxclass(z)=cjxi∈Nk(z)∑I(yi=cj)
其中 N k ( z ) N_k(z) Nk(z) 为 z z z 的最近邻的 k k k 个训练实例点集构成的集合; ( x i , y i ) (x_i,y_i) (xi,yi) 为训练实例点; I ( y i = c j ) I(y_i=c_j) I(yi=cj) 为训练实例类别的示性函数,当 y i y_i yi 为类别 c j c_j cj 时, I ( y i = c j ) = 1 I(y_i=c_j)=1 I(yi=cj)=1。
公式的含义说白了就是:对于类别集 { c 1 , c 2 , ⋯ , c K } \{c_1,c_2,\cdots,c_K\} {c1,c2,⋯,cK} 中的每一个类别 c j c_j cj “投票”, I ( y i = c j ) = 1 I(y_i=c_j)=1 I(yi=cj)=1 就是“ y i y_i yi 投 c j c_j cj 一票”, I ( y i = c j ) = 0 I(y_i=c_j)=0 I(yi=cj)=0 就是“ y i y_i yi 不投 c j c_j cj 票”,有投票权的 y i y_i yi 是 N k ( z ) N_k(z) Nk(z) 中的训练实例,求和后得到每一个类别 c j c_j cj 的总票数,总票数最高的那个类别即为待预测实例 z z z 的类别。
加距离权重的多数表决规则(博主绞尽脑汁搞懂了核函数加权法)
根据 k k k 个邻居到测试集中待预测点 z z z 的距离,加权每个邻居的“贡献”:给距离待预测点 z z z 近的训练集实例更大的权重。例如利用权重函数 w = 1 d ( x i , z ) 2 w=\frac{1}{d(x_i,z)^2} w=d(xi,z)21 或者核函数。
测试集中点 z z z 的类别 c z c_z cz 用加距离权重的多数表决准则得到的公式表达为:
c l a s s ( z ) = arg max c l a s s ( z ) = c j ∑ x i ∈ N k ( z ) w i × I ( y i = c j ) class(z)=\mathop{\arg\max}_{class(z)=c_j} \sum_{x_i\in N_k(z)}w_i\times I(y_i=c_j) class(z)=argmaxclass(z)=cjxi∈Nk(z)∑wi×I(yi=cj)
加距离权重的多数表决规则的本质原理和普通多数表决规则是一样的,除了对 N k ( z ) N_k(z) Nk(z) 中的每个训练集实例进行加权。这也符合实际意义中,更相近的点更相似,因此赋予相近的点更大的权重。
最后,博主要使出浑身解数为大家讲解一下使用核函数加权的方法。首先,了解一下有哪些核(kernel)函数:

然后,获得测试集与第 k + 1 k+1 k+1 个邻居的距离 d k + 1 d_{k+1} dk+1(即除去 k k k 个邻居后离测试集待测点最近的那个训练集实例),然后用它与 1 ∼ k 1\sim k 1∼k 个邻居的距离除以 d k + 1 d_{k+1} dk+1,这些值才是kernel函数中的自变量 u u u。最后,通过kernel函数对这些新自变量 u u u 的运算得到每个邻居的权重。
KNN回归问题
k k k 近邻法中的回归预测方法为通过求与待预测点距离最近的 k k k 个点的值的平均值得到。
k k k 近邻法特点
| 目标 | 关键的几个问题 | 是否需要标准化 | 是否容许有缺失值 | |
|---|---|---|---|---|
| 分类判别(因变量定性) | 回归(因变量定量) | |||
| 可以 | 可以 | (1)k值 | 需要 | 容许(但R代码中却不容许缺失值) |
| (2)距离度量 | ||||
| (3)核函数 | ||||
优点
- 简单高效
- 不对数据集做任何假设
- 训练阶段迅速
缺点
- 不能产生模型,因此不能观测到模型内部变量之间的关联
- 预测阶段缓慢
- 需要大量存储空间(由于 k k k 近邻法为惰性算法,所以输入训练集时并没有马上开始建模,而是存储在记忆空间中等待测试集数据输入)
- 定性变量和缺失值失需要进一步处理
k k k 近邻法评估
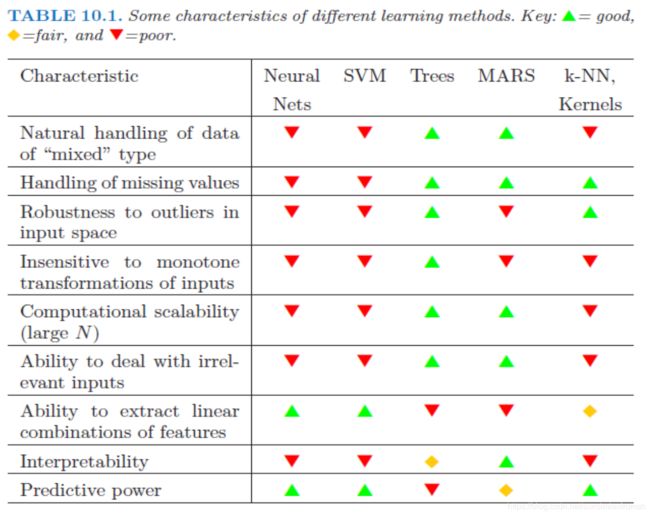
解释3:
- Natural handling of data of “mixed” type:混合型数据处理能力。混合型数据指的是数据集的特征既有定性变量也有定量变量, k k k 近邻法处理定性数据距离需要标准化,因此混合型数据处理能力不太好;
- Handling of missing values:缺失值处理能力。若数据集中有缺失值,距离也是有特定的距离度量,因此 k k k 近邻法处理缺失值能力很好;
- Robustness to outliers in input space:异常值的稳健型。若有异常值,根据 k k k 近邻法的原理,由于异常值不会在待预测点的邻域中,异常值不会参与最终的决策,故异常值对 k k k 近邻法的影响不大;
- Insensitive to monotone transformations of inputs:对单调性变换不敏感。 k k k 近邻法对单调性变换不敏感;
- Computational scalability:可扩展性。可扩展性好指的是加入新数据后,只要对原模型做些许修改就可以继续使用,由于增加新的数据就要重新划分待预测点的邻域, k k k 近邻法的可扩展性不太好;
- Ability to deal with irrelevant inputs:处理无关解释变量的能力。 k k k 近邻法无法甄别无关变量,不能将无关变挑出来剔除,处理无关变量能力比较差;
- Ability to extract linear combinations of features:获得特征的线性组合能力;
- Interpretability:可解释性。由于 k k k 近邻法本身无模型,因此可解释性不强;
- Predictive power:预测能力。 k k k 近邻法预测能力不错(对于这点,博主持怀疑态度,根据接下来的代码结果可见)。
手算例子
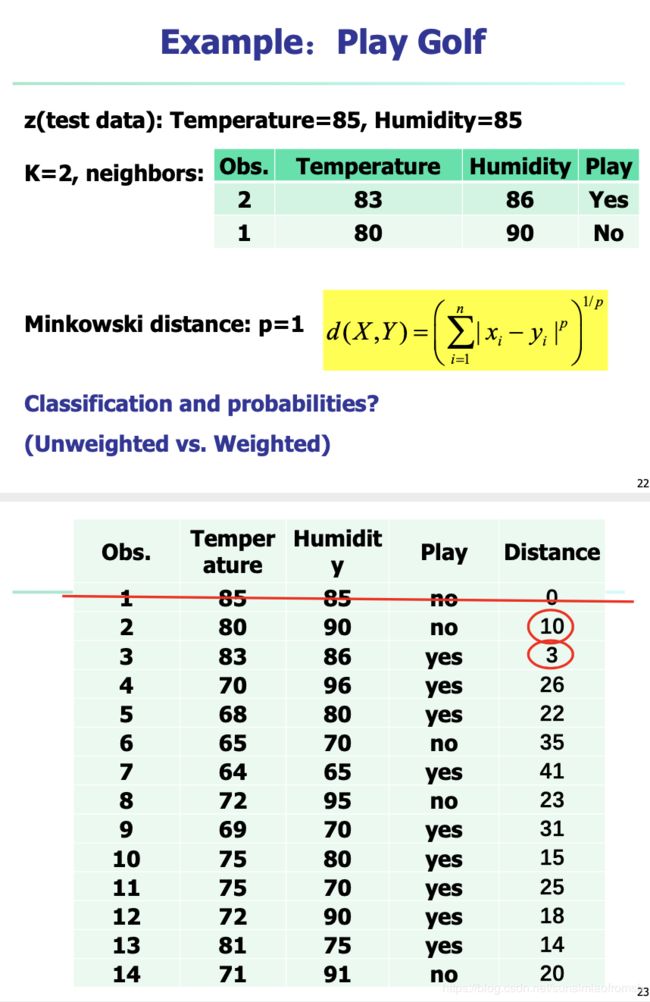
例:图中是golf例子的训练集,我们取第一个样本(去除类别)作为待预测点 z z z,取 k k k 值为2,利用闵氏距离作为距离度量。在不加距离权重和加距离权重两种情况下,计算预测样本被判为每个类别的概率和最终预测类别。
解:
首先,利用闵氏距离计算出所有点距离待测样本点的距离(即图中的distance列所示),根据事先拟定的 k k k 值为2,我们选择第2、3两个样本作为邻居,第2个样本的类别为“no”,第3个样本的类别为“yes”。接下来我们来计算概率和分类:
(1)不加距离权重的情况
P ( c l a s s ( z ) = y e s ) = ∑ x i ∈ N k ( z ) I ( y i = y e s ) k = 0 + 1 2 = 1 2 \begin{aligned} P(class(z)=yes)=\ &\frac{ \sum_{x_i\in N_k(z)}I(y_i=yes)}{k}\\ =\ &\frac{0+1}{2}\\ =\ &\frac{1}{2} \end{aligned} P(class(z)=yes)= = = k∑xi∈Nk(z)I(yi=yes)20+121
P ( c l a s s ( z ) = n o ) = ∑ x i ∈ N k ( z ) I ( y i = n o ) k = 1 + 0 2 = 1 2 \begin{aligned} P(class(z)=no)=\ &\frac{ \sum_{x_i\in N_k(z)}I(y_i=no)}{k}\\ =\ &\frac{1+0}{2}\\ =\ &\frac{1}{2} \end{aligned} P(class(z)=no)= = = k∑xi∈Nk(z)I(yi=no)21+021
预测样本被判为每个类别的概率都为0.5。
(2)加距离权重(以三角权重为例)
先构造核函数里的自变量,距离待测样本第3近的是第13个样本,因此 d k + 1 = d 3 = 14 d_{k+1}=d_3=14 dk+1=d3=14 。
u 1 = d 1 d 3 = 3 14 u_1=\frac{d_1}{d_3}=\frac{3}{14} u1=d3d1=143
u 2 = d 2 d 3 = 10 14 u_2=\frac{d_2}{d_3}=\frac{10}{14} u2=d3d2=1410
再利用核函数计算权重:
w 1 = t r i a n g l e ( u 1 ) = ( 1 − 3 14 ) I ( ∣ 3 14 ∣ ≤ 1 ) = 11 14 w_1=triangle(u_1)=(1-\frac{3}{14})I(\mid \frac{3}{14} \mid \leq1)=\frac{11}{14} w1=triangle(u1)=(1−143)I(∣143∣≤1)=1411
w 2 = t r i a n g l e ( u 2 ) = ( 1 − 10 14 ) I ( ∣ 10 14 ∣ ≤ 1 ) = 4 14 w_2=triangle(u_2)=(1-\frac{10}{14})I(\mid \frac{10}{14} \mid \leq1)=\frac{4}{14} w2=triangle(u2)=(1−1410)I(∣1410∣≤1)=144
计算加权和:
s c o r e ( z = y e s ) = ∑ i = 1 2 w i I ( y i = y e s ) = 11 14 × 1 + 4 14 × 0 = 11 14 score(z=yes)=\sum_{i=1}^2 w_i I(y_i=yes)=\frac{11}{14}\times 1+\frac{4}{14}\times 0=\frac{11}{14} score(z=yes)=i=1∑2wiI(yi=yes)=1411×1+144×0=1411
s c o r e ( z = n o ) = ∑ i = 1 2 w i I ( y i = n o ) = 11 14 × 0 + 4 14 × 1 = 4 14 score(z=no)=\sum_{i=1}^2 w_i I(y_i=no)=\frac{11}{14}\times 0+\frac{4}{14}\times 1=\frac{4}{14} score(z=no)=i=1∑2wiI(yi=no)=1411×0+144×1=144
P ( z = y e s ) = s c o r e ( z = y e s ) s c o r e ( z = y e s ) + s c o r e ( z = n o ) = 11 14 11 14 + 4 14 = 11 15 P(z=yes)=\frac{score(z=yes)}{score(z=yes)+score(z=no)}=\frac{\frac{11}{14}}{\frac{11}{14}+\frac{4}{14}}=\frac{11}{15} P(z=yes)=score(z=yes)+score(z=no)score(z=yes)=1411+1441411=1511
P ( z = n o ) = s c o r e ( z = n o ) s c o r e ( z = y e s ) + s c o r e ( z = n o ) = 4 14 11 14 + 4 14 = 4 15 P(z=no)=\frac{score(z=no)}{score(z=yes)+score(z=no)}=\frac{\frac{4}{14}}{\frac{11}{14}+\frac{4}{14}}=\frac{4}{15} P(z=no)=score(z=yes)+score(z=no)score(z=no)=1411+144144=154
预测样本被判为“yes”类别和“no”类别的概率分别为 11 15 \frac{11}{15} 1511 和 4 15 \frac{4}{15} 154,因此预测类别为“yes”类别。
代码:R语言
设定当前的工作目录:
setwd(".../data")
录入数据
alldata <- read.csv("golf.csv",header=T)
alldata
数据结果:
## Outlook Temperature Humidity Windy Play
## 1 Sunny 85 85 false no
## 2 Sunny 80 90 true no
## 3 Overcast 83 86 false yes
## 4 Rainy 70 96 false yes
## 5 Rainy 68 80 false yes
## 6 Rainy 65 70 true no
## 7 Overcast 64 65 true yes
## 8 Sunny 72 95 false no
## 9 Sunny 69 70 false yes
## 10 Rainy 75 80 false yes
## 11 Sunny 75 70 true yes
## 12 Overcast 72 90 true yes
## 13 Overcast 81 75 false yes
## 14 Rainy 71 91 true no
分类问题:投票无加权+自变量为定量变量
采用class包中的函数建模,class包是无加权权重的KNN问题。
if (!require(class)) {
install.packages("class")
library(class)
}
划分训练集和测试集。为了查看具体运作机制,下面先观察自变量为定量变量的情况,最后再观察自变量为定性变量的情况。
trainx <- alldata[-c(1,2),2:3] # 训练集(除去前两行样本作为测试集,取定量自变量)
testx <- alldata[1:2,2:3] # 测试集
trainy <- alldata[-c(1,2),5]
testy <- alldata[1:2,5]
建模:使用class包中的knn函数。
knn(trainx,testx,cl=trainy,k=2,prob=T) # 随意建立一个模型,取了k=2
## [1] yes yes
## attr(,"prob")
## [1] 1 1
## Levels: no yes
调参:使用class包中的knn.cv函数,采用留一交叉验证寻找最优的k值。
error <- rep(0,10)
for (i in 1:10){
set.seed(1)
# 设置随机数种子为1
# 这里的knn.cv是留一交叉验证,应该与随机数无关,但是我发现它与随机数有关。why?
cv1 <- knn.cv(trainx,cl=trainy, k=i, prob = TRUE)
# 设定k值的挑拣范围为1~10,knn.cv默认情况下是留一交叉验证
error[i] <- sum(as.numeric(as.numeric(cv1)!=as.numeric(trainy)))/nrow(trainx)
# k值为i时的错判率
}
error
解读一下上面求错判率的代码:as.numeric(cv1)!=as.numeric(trainy)的结果是留一交叉验证预测得到的训练集trainx中每个样本的类别,且该结果用True和False来表征。通过as.numeric(as.numeric(cv1)!=as.numeric(trainy))即可把True和False组成的向量转变为0和1组成的向量,对该变量求和后即是错判的样本个数。再除以nrow(trainx)则是错判率。不同k值的错判率结果如下所示:
## [1] 0.5833333 0.5833333 0.4166667 0.3333333 0.2500000 0.2500000 0.2500000
## [8] 0.2500000 0.2500000 0.2500000
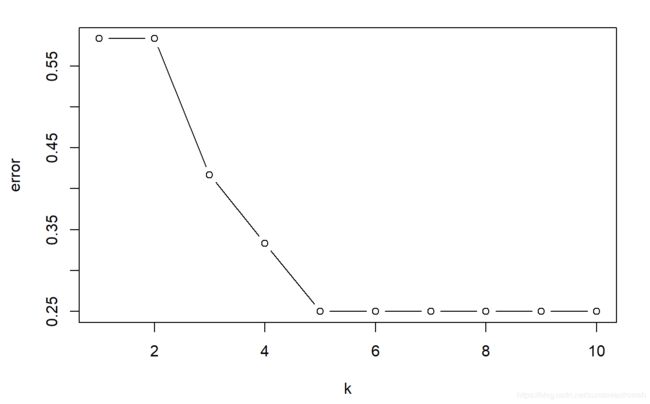
plot(error,type="b",xlab="k")
发现k>=5时错判率达到最小,下面取k=5进行预测。
predict <- knn(trainx,testx,cl=trainy,k=5,prob=T)
table(testy,predict)
## predict
## testy no yes
## no 0 2
## yes 0 0
预测效果糟糕,大概只采用了两个定量自变量的原因!
分类问题:投票有加权+自变量为定量变量(手算问题核验)
采用kknn包中的函数建模,kknn包可以做有加权权重的KNN问题。
if (!require(kknn)) {
install.packages("kknn")
library(kknn)
}
划分训练集和测试集。
train <- alldata[-1,c(2:3,5)] # 训练集(和class包不一样,不需要把自变量和因变量分开)
testx <- alldata[1,2:3] # 测试集(只拿第一个样本作为预测集)
coly <- 3 # y所在的列号
names(train)[coly] <- "y" # 命名因变量的列
查看邻居和距离等作用机制。为便于查看,下面使用了scale=F,但通常建模时应设置scale=T。建模:利用k值为2。
model.kknn <- kknn(y~.,train,testx,k=2,scale=F,distance=1,kernel= "rectangular")
model.kknn$C # 邻居的观测值号
kknn函数参数解读:distance即为距离度量里闵氏距离的p(特别地,p=1时为曼哈顿距离,p=2时为欧式距离);kernel为加权的核函数,可以选择的值有"rectangular"(无加权knn),“triangular”,“epanechnikov”(beta(2,2)),“biweight” (beta(3,3)),“triweight”(beta(4,4)),“cos”,“inv”,“gaussian”,“rank"和"optimal”。
## [1] 2 1
这与我们前面的手算题结果是一样的。
train[model.kknn$C,] # 查看邻居
## Temperature Humidity y
## 3 83 86 yes
## 2 80 90 no
需要注意的是,邻居的观测值号是在训练集中的序号,而非在原始整个数据集中的样本编号。这个例子中,邻居观测值序号为2和1,而它们在原始数据集中的样本编号是3和2。
testx
## Temperature Humidity
## 1 85 85
model.kknn$D # 邻居与测试集点的距离
## [1] 3 10
结合测试集与两个邻居的数据,可以看到,测试集与第一个邻居的距离是|85-83|+|85-86|=3,与第二个邻居的距离是|85-80|+|85-90|=10(用的是曼哈顿距离)。
model.kknn$W # 邻居的权重
## [,1] [,2]
## [1,] 1 1
由于加权的kernel函数为“rectangular”(无加权),故二者权重一致,都为1。
model.kknn$CL #邻居的类别
## [,1] [,2]
## [1,] "yes" "no"
model.kknn$prob # 预测的概率
## no yes
## [1,] 0.5 0.5
由于两个邻居的权重都为1,故为“no”和“yes”的概率各为0.5。
model.kknn2 <- kknn(y~.,train,testx,k=2,scale=F,distance=1,kernel= "triangular")
model.kknn2$C # 邻居的观测值号
## [1] 2 1
train[model.kknn2$C,]#查看邻居
## Temperature Humidity y
## 3 83 86 yes
## 2 80 90 no
model.kknn2$D #邻居与它的距离
## [1] 3 10
model.kknn2$W # 邻居的权重
## [,1] [,2]
## [1,] 0.7857143 0.2857143
由于加权的kernel函数为“triangular”,故二者权重不一致。在这个kknn函数中,权重的计算方法是获得测试集与第k+1个邻居的距离 D k + 1 D_{k+1} Dk+1,然后用它与1~k个邻居的距离除以 D k + 1 D_{k+1} Dk+1,这些值才是kernel函数中的自变量。本例中,k=2,可以获得测试集与第3个邻居的距离为14(大家可以自己确认下),“triangular”函数的表达式(1−|u|)I(|u|≤1),因此,权重分别为1−3/14=0.79和1−10/14=0.29。需要注意的是,这两个权重之和不等于1,但没有关系,这在后面计算预测概率时会进行调整。
model.kknn2$CL # 邻居的类别
## [,1] [,2]
## [1,] "yes" "no"
model.kknn2$prob # 预测的概率
## no yes
## [1,] 0.2666667 0.7333333
这里两个邻居的权重不一致。预测为“yes”的概率应为0.79/(0.79+0.29)=0.73(因为第1个邻居是“yes”,其权重为0.79),预测为“no”的概率应为0.29/(0.29+0.79)=0.27(因为第2个邻居是“no”,其权重为0.29)。
# 首先,确定最优参数kernel
# 取distance=2
model.tkknn <- train.kknn(y~.,train,kernel = c("rectangular", "triangular", "epanechnikov", "optimal"),distance=2,scale=T)
plot(model.tkknn)
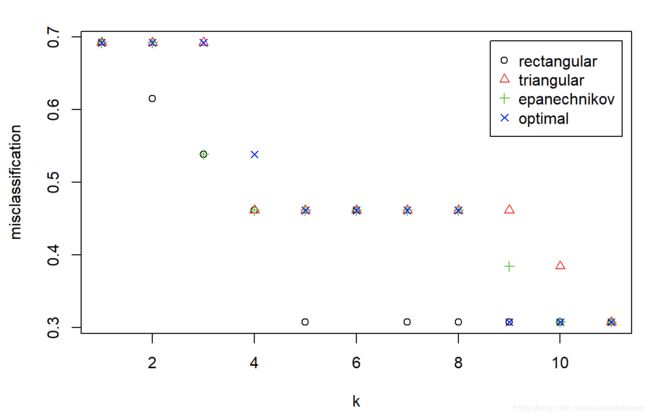
model.tkknn$MISCLASS #显示错误率
## rectangular triangular epanechnikov optimal
## 1 0.6923077 0.6923077 0.6923077 0.6923077
## 2 0.6153846 0.6923077 0.6923077 0.6923077
## 3 0.5384615 0.6923077 0.5384615 0.6923077
## 4 0.4615385 0.4615385 0.4615385 0.5384615
## 5 0.3076923 0.4615385 0.4615385 0.4615385
## 6 0.4615385 0.4615385 0.4615385 0.4615385
## 7 0.3076923 0.4615385 0.4615385 0.4615385
## 8 0.3076923 0.4615385 0.4615385 0.4615385
## 9 0.3076923 0.4615385 0.3846154 0.3076923
## 10 0.3076923 0.3846154 0.3076923 0.3076923
## 11 0.3076923 0.3076923 0.3076923 0.3076923
注意看,第一列是k的取值,也就是说这里自动搜索k取1至11的情况。k的最大搜索值可由kmax参数设置。若不设置kmax,它自动取为训练集样本量减2。
model.tkknn
##
## Call:
## train.kknn(formula = y ~ ., data = train, distance = 2, kernel = c("rectangular", "triangular", "epanechnikov", "optimal"), scale = T)
##
## Type of response variable: nominal
## Minimal misclassification: 0.3076923
## Best kernel: rectangular
## Best k: 5
输出最优参数情况,显示最优的kernel为"rectangular",k=5。查看最优情况下的拟合情况(kernel=“rectangular”,k=5位于第5个位置):
model.tkknn$fitted.values[[5]]
## [1] yes yes yes yes yes yes yes yes yes yes yes yes yes
## attr(,"kernel")
## [1] rectangular
## attr(,"k")
## [1] 5
## Levels: no yes
混淆矩阵:
table(train[,coly],model.tkknn$fitted.values[[5]])
##
## no yes
## no 0 4
## yes 0 9
# 取distance=1
model.tkknn2 <- train.kknn(y~.,train,kernel = c("rectangular", "triangular", "epanechnikov", "optimal"),distance=1,scale=T)
plot(model.tkknn2)
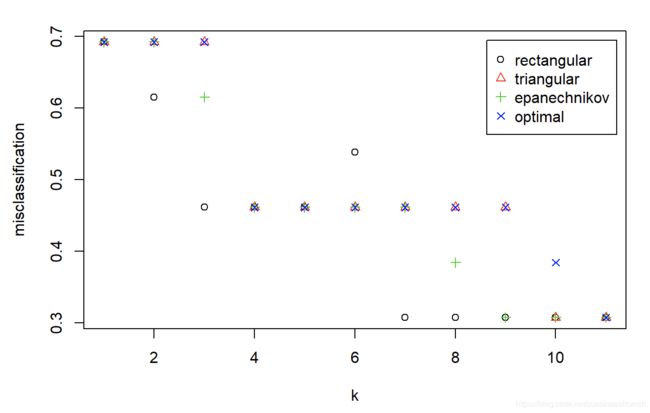
model.tkknn2$MISCLASS
## rectangular triangular epanechnikov optimal
## 1 0.6923077 0.6923077 0.6923077 0.6923077
## 2 0.6153846 0.6923077 0.6923077 0.6923077
## 3 0.4615385 0.6923077 0.6153846 0.6923077
## 4 0.4615385 0.4615385 0.4615385 0.4615385
## 5 0.4615385 0.4615385 0.4615385 0.4615385
## 6 0.5384615 0.4615385 0.4615385 0.4615385
## 7 0.3076923 0.4615385 0.4615385 0.4615385
## 8 0.3076923 0.4615385 0.3846154 0.4615385
## 9 0.3076923 0.4615385 0.3076923 0.4615385
## 10 0.3076923 0.3076923 0.3076923 0.3846154
## 11 0.3076923 0.3076923 0.3076923 0.3076923
model.tkknn2
##
## Call:
## train.kknn(formula = y ~ ., data = train, distance = 1, kernel = c("rectangular", "triangular", "epanechnikov", "optimal"), scale = T)
##
## Type of response variable: nominal
## Minimal misclassification: 0.3076923
## Best kernel: rectangular
## Best k: 7
建模:采用最优参数做预测(distance=2):
model.kknn <- kknn(y~.,train,testx,k=model.tkknn$best.parameters$k,scale=T,distance=2,kernel=model.tkknn$best.parameters$kernel)
model.kknn$C # 邻居的观测值号
## [1] 2 1 12 9 10
train[model.kknn$C,] # 查看邻居
## Temperature Humidity y
## 3 83 86 yes
## 2 80 90 no
## 13 81 75 yes
## 10 75 80 yes
## 11 75 70 yes
model.kknn$D # 邻居与它的距离
## [1] 0.3505430 0.9659556 1.1561437 1.7527150 2.1983476
model.kknn$W # 邻居的权重
## [,1] [,2] [,3] [,4] [,5]
## [1,] 1 1 1 1 1
model.kknn$CL # 邻居的类别
## [,1] [,2] [,3] [,4] [,5]
## [1,] "yes" "no" "yes" "yes" "yes"
model.kknn$prob # 预测的概率
## no yes
## [1,] 0.2 0.8
summary(model.kknn)
##
## Call:
## kknn(formula = y ~ ., train = train, test = testx, k = model.tkknn$best.parameters$k, distance = 2, kernel = model.tkknn$best.parameters$kernel, scale = T)
##
## Response: "nominal"
## fit prob.no prob.yes
## 1 yes 0.2 0.8
fit <- fitted(model.kknn)
fit
## [1] yes
## Levels: no yes
回归问题:有加权+训练集为混合性数据
y为数值型的例子——采用rpart包中的car.test.frame数据
if (!require(rpart)) {
install.packages("rpart")
library(rpart)
} # 为了使用该包中的数据集car.test.frame
data(car.test.frame) # 加载数据集
str(car.test.frame) # 查看数据集中的变量
## 'data.frame': 60 obs. of 8 variables:
## $ Price : int 8895 7402 6319 6635 6599 8672 7399 7254 9599 5866 ...
## $ Country : Factor w/ 8 levels "France","Germany",..: 8 8 5 4 3 6 4 5 3 3 ...
## $ Reliability: int 4 2 4 5 5 4 5 1 5 NA ...
## $ Mileage : int 33 33 37 32 32 26 33 28 25 34 ...
## $ Type : Factor w/ 6 levels "Compact","Large",..: 4 4 4 4 4 4 4 4 4 4 ...
## $ Weight : int 2560 2345 1845 2260 2440 2285 2275 2350 2295 1900 ...
## $ Disp. : int 97 114 81 91 113 97 97 98 109 73 ...
## $ HP : int 113 90 63 92 103 82 90 74 90 73 ...
dim(car.test.frame) # 查看数据维度
## [1] 60 8
下面,查看邻居和距离等作用机制,并不涉及建模
train <- car.test.frame[-1,c(1,4)] # 训练集
test <- car.test.frame[1,c(1,4)] # 测试集
coly <- 2 # y所在的列号
names(train)[coly] <- "y"
model.kknn <- kknn(y~.,train,test,k=2,scale=F,distance=1,kernel="rectangular")
model.kknn$C # 邻居的观测值号
## [1] 10 5
train[model.kknn$C,] # 查看邻居
## Price y
## Toyota Corolla 4 8748 29
## Mercury Tracer 4 8672 26
model.kknn$D # 邻居与它的距离
## [1] 147 223
model.kknn$W # 邻居的权重
## [,1] [,2]
## [1,] 1 1
model.kknn$CL # 邻居的数值
## [,1] [,2]
## [1,] 29 26
model.kknn$prob # y为定量数据时,prob不存在
## NULL
model.fit <- fitted(model.kknn)
model.fit
## [1] 27.5
可以看出最终的预测值27.5为邻居因变量29和26的平均值。
回归问题:有加权+训练集为混合性数据+含缺失数据
经测试,运用kknn函数,测试集不能含有缺失值(对于参与建模的变量),对于训练集中有缺失值的情况,可以运行出结果,但是发现它只在无缺失值的样本中找邻居,而且返回的距离值有些异常。
n <- round(2/3*nrow(car.test.frame))
set.seed(1)
sub_train=sample(1:nrow(car.test.frame),n)
train <- car.test.frame[sub_train,]
test <- car.test.frame[-sub_train,]
summary(test) # 测试集中的Reliability有3个值缺失
## Price Country Reliability Mileage
## Min. : 7254 USA :10 Min. :1.000 Min. :18.00
## 1st Qu.:10424 Japan : 5 1st Qu.:2.000 1st Qu.:21.75
## Median :12363 Japan/USA: 2 Median :3.000 Median :23.00
## Mean :13010 Korea : 2 Mean :3.235 Mean :23.85
## 3rd Qu.:16194 Sweden : 1 3rd Qu.:4.000 3rd Qu.:25.00
## Max. :23300 France : 0 Max. :5.000 Max. :33.00
## (Other) : 0 NA's :3
## Type Weight Disp. HP
## Compact:7 Min. :2275 Min. : 97.0 Min. : 74.0
## Large :1 1st Qu.:2749 1st Qu.:130.2 1st Qu.:101.0
## Medium :6 Median :2930 Median :147.0 Median :110.0
## Small :3 Mean :2952 Mean :151.6 Mean :120.8
## Sporty :1 3rd Qu.:3231 3rd Qu.:180.2 3rd Qu.:145.5
## Van :2 Max. :3665 Max. :231.0 Max. :165.0
##
coly <- 4 # y所在的列号
names(train)[coly] <- "y"
model.kknn <- kknn(y~.,train,test[,-coly],kernel = "rectangular",k=5,distance=1,scale=T)
model.kknn$fitted.values # 输出17个预测值
## [1] 26.8 30.6 29.4 25.4 23.8 25.4 25.4 24.4 21.6 25.6 22.4 21.0 21.2 21.2
## [15] 23.6 21.0 20.8
nrow(test)
## [1] 20
测试集中有20个样本。表明测试集中含有缺失值的3个样本没有获得预测值。如果把含有缺失值的变量Reliability踢出模型,就会有20个输出值:
model.kknn <- kknn(y~.,train[,-3],test[,-coly],kernel = "rectangular",k=5,distance=1,scale=T)
model.kknn$fitted.values # 输出20个值
## [1] 29.6 29.4 31.8 28.8 25.4 21.8 26.6 25.0 25.0 20.6 25.4 21.4 21.2 25.6
## [15] 21.0 21.6 22.8 20.2 20.6 19.4
测试集的Country中含有Sweden,而训练集中没有,KKNN忽略了这种情况,仍然给出了预测值。
查看模型效果
if (!require(caret)) {
install.packages("caret")
library(caret)
} # 为了使用其中的postResample函数,以评价模型效果
measure.kknn <- postResample(model.kknn$fitted.values,test[,coly])
measure.kknn
## RMSE Rsquared MAE
## 2.2649503 0.6588085 1.8900000
如果不想牺牲变量Reliability,只能分别操作
test2 <- test[complete.cases(test),]
dim(test2) # 获得17个无缺失的cases
## [1] 17 8
model.kknn.com <- kknn(y~.,train,test2[,-coly],kernel = "rectangular",k=5,distance=1,scale=T)
model.kknn.com$fitted.values # 输出17个值
## [1] 26.8 30.6 29.4 25.4 23.8 25.4 25.4 24.4 21.6 25.6 22.4 21.0 21.2 21.2
## [15] 23.6 21.0 20.8
test3<- test[!complete.cases(test),]
dim(test3) # 获得3个有缺失的cases
## [1] 3 8
model.kknn.mis <- kknn(y~.,train[,-3],test3[,-coly],kernel = "rectangular",k=5,distance=1,scale=T)
model.kknn.mis$fitted.values # 输出3个值
## [1] 28.8 25.6 19.4
testfit_bind <- c(model.kknn.com$fitted.values,model.kknn.mis$fitted.values)
test_rbind <- rbind(test2,test3)
模型效果
measure.kknn2 <- postResample(testfit_bind,test_rbind[,coly])
measure.kknn2
## RMSE Rsquared MAE
## 2.2378561 0.6480338 1.8000000
结果显示,分开操作获得的模型优于变量Reliability被整个踢出的模型。
定性变量间的距离
golf.train3 <- alldata[-1,c(1,5)]
golf.test3 <- alldata[1,c(1,5)]
golf.kknn3 <- kknn(Play~.,golf.train3,golf.test3,k=6,scale=F,distance=1,kernel= "rectangular")
golf.kknn3$C # 邻居的观测值号
## [1] 1 10 7 8 5 2
golf.train3[golf.kknn3$C,] # 查看邻居
## Outlook Play
## 2 Sunny no
## 11 Sunny yes
## 8 Sunny no
## 9 Sunny yes
## 6 Rainy no
## 3 Overcast yes
golf.kknn3$D # 邻居与它的距离(这里的X为Outlook有3个取值)
## [1] 0.0000000 0.0000000 0.0000000 0.0000000 0.6666667 0.6666667
对于定性的自变量,推测这里计算距离的方式是:产生与自变量取值个数m相同的虚拟变量(取值为0或1),然后利用虚拟变量来计算距离,公式为 ( ∣ X − Y ∣ D m ) 1 D (\frac{|X−Y|^D}{m})^{\frac{1}{D}} (m∣X−Y∣D)D1。本例中,自变量取值个数m=3
,距离参数distance=1,测试集的自变量取值为Sunny,故前4个邻居与它的距离为0;第5个邻居与它的距离为 ( ∣ 0 − 0 ∣ + ∣ 0 − 1 ∣ + ∣ 1 − 0 ∣ ) 3 = 0.67 \frac{(|0−0|+|0−1|+|1−0|)}{3}=0.67 3(∣0−0∣+∣0−1∣+∣1−0∣)=0.67,第6个邻居类似。
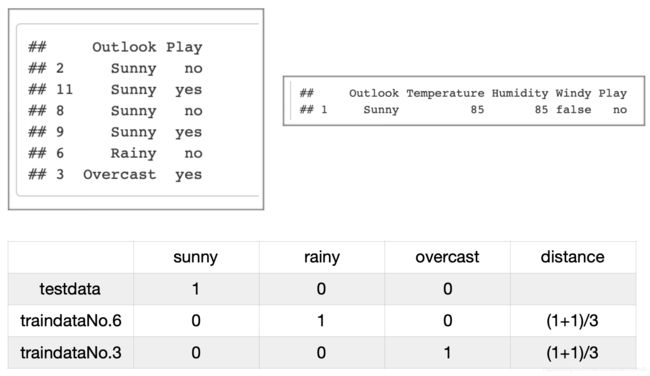
解释:图中的No.6即训练集第5个邻居,为了一眼能看懂,因此博主偷懒取了它在训练集中的编号。右上这张图为测试集,左上这张图为训练集。
golf.kknn3 <- kknn(Play~.,golf.train3,golf.test3,k=6,scale=F,distance=2,kernel= "rectangular")
golf.kknn3$C # 邻居的观测值号
## [1] 1 10 7 8 5 2
golf.train3[golf.kknn3$C,] # 查看邻居
## Outlook Play
## 2 Sunny no
## 11 Sunny yes
## 8 Sunny no
## 9 Sunny yes
## 6 Rainy no
## 3 Overcast yes
golf.kknn3$D # 邻居与它的距离(这里的X为Outlook有3个取值)
## [1] 0.0000000 0.0000000 0.0000000 0.0000000 0.8164966 0.8164966
按照上面的计算公式,与第5个邻居的距离应为 [ ( ∣ 0 − 0 ∣ 2 + ∣ 0 − 1 ∣ 2 + ∣ 1 − 0 ∣ 2 ) 3 ] 1 2 = 0.82 [\frac{(|0−0|^2+|0−1|^2+|1−0|^2)}{3}]^{\frac{1}{2}}=0.82 [3(∣0−0∣2+∣0−1∣2+∣1−0∣2)]21=0.82。
golf.train4 <- alldata[-1,c(4,5)]
golf.test4 <- alldata[1,c(4,5)]
golf.kknn4 <- kknn(Play~.,golf.train4,golf.test4,k=9,scale=F,distance=1,kernel= "rectangular")
golf.kknn4$C # 邻居的观测值号
## [1] 9 2 3 4 7 8 12 1 6
golf.train4[golf.kknn4$C,] # 查看邻居
## Windy Play
## 10 false yes
## 3 false yes
## 4 false yes
## 5 false yes
## 8 false no
## 9 false yes
## 13 false yes
## 2 true no
## 7 true yes
golf.kknn4$D # 邻居与它的距离(这里的X为Windy仅有2个取值)
## [1] 0 0 0 0 0 0 0 1 1
这里的自变量取值个数m=2。按照上面的计算公式,与第8和第9个邻居的距离应为 ( ∣ 1 − 0 ∣ + ∣ 0 − 1 ∣ ) 2 = 1 \frac{(|1−0|+|0−1|)}{2}=1 2(∣1−0∣+∣0−1∣)=1。
代码:Python
sklearn库的KNeighborsClassifier函数简介
sklearn.neighbors库中的KNeighborsClassifier函数讲解4:
KNeighborsClassifier(n_neighbors = 5,
weights='uniform',
algorithm = '',
leaf_size = '30',
p = 2,
metric = 'minkowski',
metric_params = None,
n_jobs = None
)
n_neighbors:这个值就是指 KNN 中的 “K”值了。前面说到过,通过调整 K 值,算法会有不同的效果。weights(距离权重):最普遍的 KNN 算法无论距离如何,权重都一样,但有时候我们想搞点特殊化,比如距离更近的点让它更加重要。这时候就需要 weight 这个参数了,这个参数有三个可选参数的值,决定了如何分配权重。参数选项如下:
•uniform:不管远近权重都一样,就是最普通的 KNN 算法的形式,即R语言中的kernel="rectangular"。
•distance:权重和距离成反比,距离预测目标越近具有越高的权重。
• 自定义函数:自定义一个函数,根据输入的坐标值返回对应的权重,达到自定义权重的目的。algorithm:在 sklearn 中,要构建 KNN 模型有三种构建方式,1. 暴力法,就是直接计算距离存储比较的那种方法;2. 使用 kd 树构建 KNN 模型;3. 使用球树构建。 其中暴力法适合数据较小的方式,否则效率会比较低。如果数据量比较大一般会选择用 KD 树构建 KNN 模型,而当 KD 树也比较慢的时候,则可以试试球树来构建 KNN。参数选项如下:brute:蛮力实现。kd_tree:KD 树实现 KNN 算法。ball_tree:球树实现 KNN 算法。auto: 默认参数,自动选择合适的方法构建模型。
不过当数据较小或比较稀疏时,无论选择哪个最后都会使用brute。
leaf_size:如果是选择蛮力实现,那么这个值是可以忽略的,当使用KD树或球树,它就是是停止建子树的叶子节点数量的阈值。默认30,但如果数据量增多这个参数需要增大,否则速度过慢不说,还容易过拟合。p:和metric结合使用的,当metric参数是"minkowski"的时候,p=1为曼哈顿距离,p=2为欧式距离。默认为p=2。metric:指定距离度量方法,一般都是使用欧式距离。euclidean:欧式距离。Manhattan:曼哈顿距离。chebyshev:切比雪夫距离。minkowski: 闵可夫斯基距离,默认参数。
n_jobs:指定多少个CPU进行运算,默认是-1,也就是全部都算。
import pandas as pd
import numpy as np
from sklearn.neighbors import KNeighborsClassifier # knn分类器
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import OneHotEncoder
from sklearn.pipeline import make_pipeline
以golf数据为例,设置路径:
path = '.../data/'
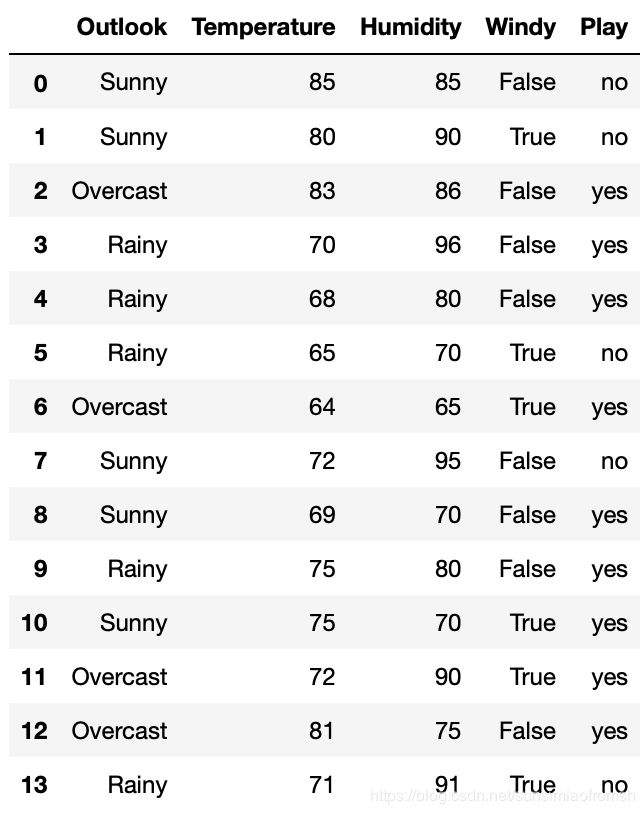
alldata = pd.read_csv(path + 'golf.csv')
alldata
alldata.info()
分类问题:定量变量的情况
划分训练集和测试集:
X_train = alldata.iloc[1:,[1,2]] # 训练集
X_test = alldata.iloc[0,[1,2]] # 测试集
X_test = np.array(X_test).reshape(1, -1)
# sklearn中,所有的数据都应该是二维矩阵,只给单独一行或一列就不符合了(因为这里只有一个样本数据),需要使用.reshape(1,-1)进行转换,不然后面无法预测
y_train = alldata.iloc[1:,4]
y_test = alldata.iloc[0,4]
等权重
建模:为便于探索,先不将X标准化处理。
knn = KNeighborsClassifier(n_neighbors=2,
p=1,
metric='minkowski',
weights='uniform') # 为便于探索,先不将X标准化处理
knn2 = knn.fit(X_train,y_train)
查看与邻居的距离及邻居的编号:
knn2.kneighbors(X_test)
(array([[ 3., 10.]]), array([[1, 0]]))
邻居分别是训练集中的第0和1个样本,它们与测试集的距离分别为3和10。
预测类别:
knn2.predict(X_test)
array(['no'], dtype=object)
预测y取各值的概率(应该是按y的取值字母顺序排列的):
knn2.predict_proba(X_test)
array([[0.5, 0.5]])
按距离加权
建模:
knn_distance = KNeighborsClassifier(n_neighbors=2,
p=1,
metric='minkowski',
weights='distance')
knn2 = knn_distance.fit(X_train,y_train)
查看与邻居的距离及邻居的编号:
knn2.kneighbors(X_test)
(array([[ 3., 10.]]), array([[1, 0]]))
邻居仍然不变。
预测类别:
knn2.predict(X_test)
array(['yes'], dtype=object)
预测y取各值的概率:
knn2.predict_proba(X_test)
array([[0.23076923, 0.76923077]])
预测y取各值的概率(一个值为3/13,另一个为10/13)。
分类问题:定性变量的情况
划分训练集和测试集:
X_train = alldata.iloc[1:,[0,3]] # 训练集
X_test = alldata.iloc[0,[0,3]] # 测试集
X_test = np.array(X_test).reshape(1, -1)
y_train = alldata.iloc[1:,4]
y_test = alldata.iloc[0,4]
knn = KNeighborsClassifier(n_neighbors=3,
p=1,
metric='minkowski',
weights='uniform')
发现KNeighborsClassifier不能自动处理取值为字符串型的定性变量,必须先做独热编码。
独热编码
encoder = OneHotEncoder()
X_OH = pd.DataFrame(encoder.fit_transform(X_train).toarray())
# 每个取值变为1个虚拟变量
X_OH
X_OHtest = pd.DataFrame(encoder.transform(X_test).toarray())
X_OHtest
查看与邻居的距离及邻居的编号:
knn3 = knn.fit(X_OH,y_train)
knn3.kneighbors(X_OHtest)
(array([[0., 0., 2.]]), array([[6, 7, 1]]))
预测类别:
knn3.predict(X_OHtest)
array(['yes'], dtype=object)
预测y取各值的概率:
knn3.predict_proba(X_OHtest)
# 尝试了将weights设置为distance,发现y=no的概率变为了0.5,我猜想应该是这里出现了距离为0的情况,将距离放在分母后就成了无穷大造成的
array([[0.33333333, 0.66666667]])
Iris数据调参案例
录入数据:
from sklearn import datasets
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
iris = datasets.load_iris() #鸢尾花
X = iris.data # 数据
y = iris.target # 标签
利用cross_val_score函数调整参数k值,选择范围为1~20:
k_range = range(1, 21)
k_error = []
#循环,取k=1到k=20,查看误差效果
for k in k_range:
knn = KNeighborsClassifier(n_neighbors=k)
scores = cross_val_score(knn, X, y, cv=6, scoring='accuracy')
# cv:选择每次测试折数,这里是按照 5:1 划分训练集和测试集;accuracy:评价指标是准确度,可以省略使用默认值,具体使用参考下面
k_error.append(1 - scores.mean())
k_error
[0.040000000000000036,
0.06000000000000005,
0.033333333333333326,
0.033333333333333326,
0.033333333333333326,
0.033333333333333326,
0.026666666666666727,
0.033333333333333326,
0.026666666666666727,
0.040000000000000036,
0.026666666666666727,
0.020000000000000018,
0.026666666666666727,
0.033333333333333326,
0.026666666666666727,
0.026666666666666727,
0.026666666666666727,
0.033333333333333326,
0.033333333333333326,
0.033333333333333326]
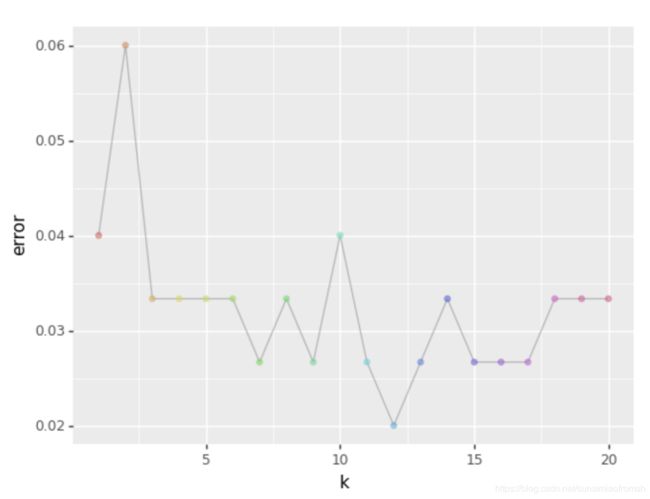
best_k = k_error.index(min(k_error))
print("best k is: ", best_k+1)
print("best score is: ", min(k_error))
最优参数值及最小错判率:
best k is: 12
best score is: 0.020000000000000018
df_k_error = pd.DataFrame({'k': range(1, 21), 'error': k_error},
index=range(1, 21))
# 画图,x轴为k值,y值为误差值
from plotnine import *
(ggplot(df_k_error, aes(x='k', y='error', color='factor(k)'))
+ geom_line(color='grey', alpha=0.5)
+ geom_point(alpha=0.5))
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets
Iris数据画分类效果图案例
导入数据
iris = datasets.load_iris()
x = iris.data[:, :2]
# 我们只采用前两个feature,方便画图在二维平面显示
y = iris.target
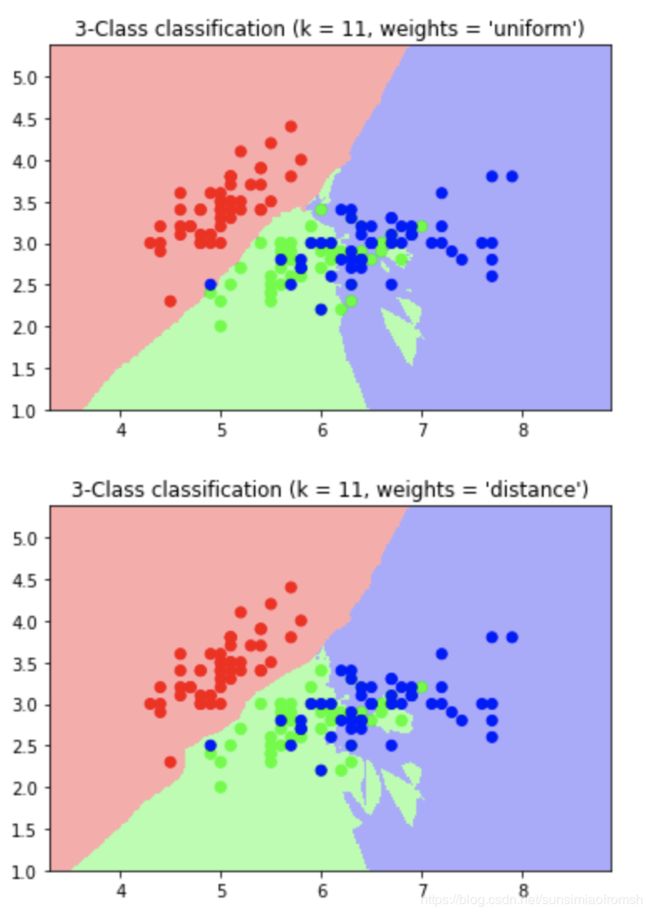
按两种距离加权的方式画knn模型的预测分类图[^5]:
n_neighbors = best_k
h = .02 # 网格中的步长
# 创建彩色的图,cmap_light和cmap_bold是配好的色系
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
# weights是KNN模型中的一个参数,上述参数介绍中有介绍,这里绘制两种权重参数下KNN的效果图
for weights in ['uniform', 'distance']:
# 创建了一个knn分类器的实例,并拟合数据。
clf = neighbors.KNeighborsClassifier(n_neighbors, weights=weights)
clf.fit(x, y)
# 绘制决策边界。为此,我们将为每个分配一个颜色
# 来绘制网格中的点 [x_min, x_max]x[y_min, y_max].
x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# meshgrid函数通常使用在数据的矢量化上。它适用于生成网格型数据,可以接受两个一维数组生成两个二维矩阵,对应两个数组中所有的(x,y)对
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# np.c_按行转换成矩阵;np_r按列转换成矩阵
# 将结果放入一个彩色图中
Z = Z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx, yy, Z, cmap=cmap_light)
# 绘制训练点
plt.scatter(x[:, 0], x[:, 1], c=y, cmap=cmap_bold)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title("3-Class classification (k = %i, weights = '%s')" % (n_neighbors, weights))
plt.show()
参考资料
李航. 统计学习方法, 2015, 清华大学出版社 ↩︎
CSDN博主:Miracle8070. 《白话机器学习算法理论+实战之K近邻算法》
https://blog.csdn.net/wuzhongqiang/article/details/104295388 ↩︎The Elements of Statistical Learning ↩︎
博客园博主:zzzzMing -大数据技术. 《深入浅出KNN算法(二) sklearn KNN实践》
https://www.cnblogs.com/listenfwind/p/10685192.html ↩︎