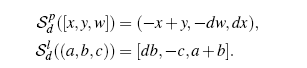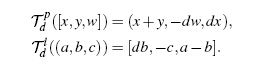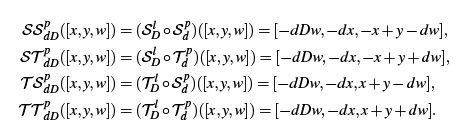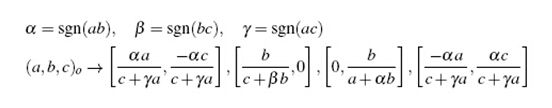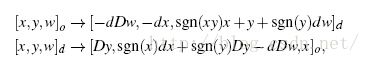平行坐标系下采用CHT方法检测自然图像中的消失点(VanishingPoint)

最近做了一些跟VanishingPoint相关的工作，所以在这里记录一下。

主要参考的的是Markéta Dubská发表再BMVC上的一篇paper——《Real Projective Plane Mapping for Detection of Orthogonal Vanishing Points》。

这个方法通过一个巧妙而简单的线性变换将一个无限大的空间变为有限空间，这就让我们能对空间进行栅格化处理，采用类似于霍夫变换中的voting方法，通过投票的方式选出VanishingPoint，对于自然图像中的VanishingPoint有不错的检测效果。

一、一些概念：

1、消失点VanishingPoint

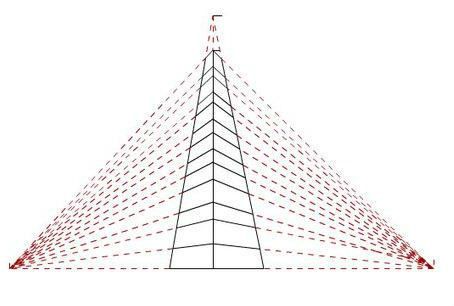
VP点（消失点）是指平行直线的交点。在物理空间中，平行的直线只能在无穷远处相交，因此VP点是无穷远处。但在透视图，两条平行线会很容易相交于一点，这一点即是VP点。如图，图中有三个消失点。而且这三个点分别对应立方体长、宽、高的消失点，我们已知立方体的长宽高是正交的，因此这三个点之间可以互相称为正交消失点。paper里最后使用了这个先验知识来校正。

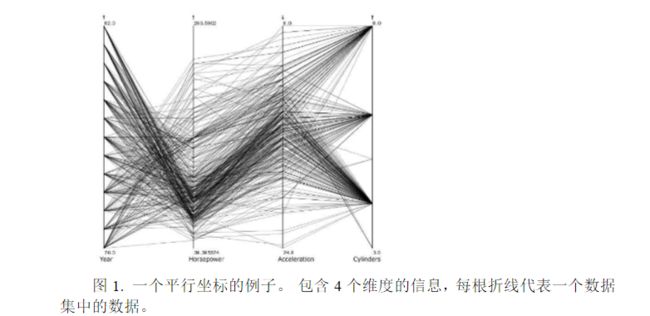
2、平行坐标系（Parallel Coordinate，PC)

笛卡尔坐标系很难表示三维以上的空间。因此便出现了平行坐标系，当它需要表示N维空间中的一个点时，它需要有N条等间距的平行轴。第K条轴代表第K维，每一维上的坐标代表这个点在这一维上的投影，例如下图的一个四维空间，一个点由四段折线表示。更多关于PC的相关内容可以参考相关资料。

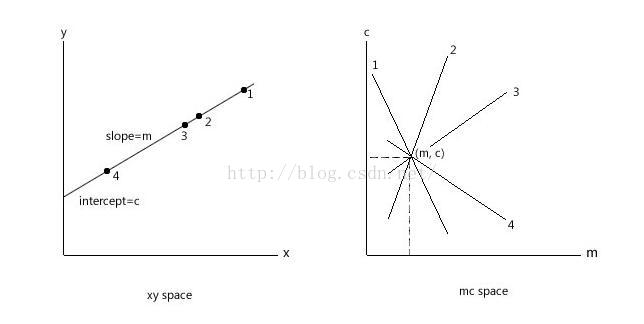
3、霍夫变换（Hough Transform，HT）

霍夫变换是一种较常用的检测直线的方法。例如一条直线y=mx+c，在X,Y坐标系下图形为一条直线，而当变换到M,C坐标系时则图形为一个点。同理，X,Y坐标系下的一个点，变换到M,C坐标系则编程一条直线。这就是霍夫变换的核心思想，变量与参数互相交换一下，则：线→点，点→线

因此，当已知若干点，需要求出它们所在的直线时，便可通过霍夫变换，将所有点变换为霍夫空间里的线，因为共线点经过变换后会变成相交于一点的线，此时只需进行栅格化处理，通过voting的方式便可选出权值最大的点，这个点即代表了所求直线，只需将其变换回原坐标系即可。

3、级联霍夫变换（Cascaded Hough Transform，CHT）

在这里要引入paper里面的一个概念：CHT——级联霍夫变换。所谓级联，就是指连续做两次霍夫变换。前面提到霍夫变换的变换关系是：线→点，点→线，那做两次霍夫变换的结果就变成了：线→线，点→点。

要注意的是，霍夫变换有许多种参数化的方法。前面提到的霍夫变换的参数化方法是M-C（斜率-截距）。但在此篇paper里，作者将霍夫变换与平行坐标系结合，提出了另一种叫PClines的参数化方法（可参见作者的另一篇paper：《PClines – Line Detection Using Parallel Coordinates》）。

PClines的参数化方式如下图：

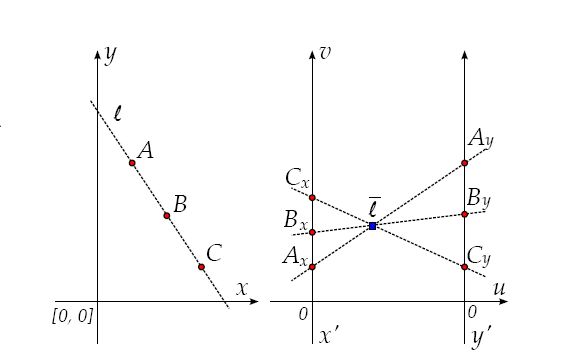
 首先，第一次S变换将原X-Y坐标系下的点和直线变换到了平行坐标系（PC）下。可以看到X-Y坐标系中的共线的三个二维点对应到PC坐标系中的三条直线（Xp轴对应X坐标，Yp轴对应Y坐标，将Xp与Yp连接便形成一条直线）。

也可以看到X-Y坐标系下的三条直线在PC坐标系下变成了三个点（因为在X-Y坐标系下三条直线交于B点，因此，在PC坐标系下，它们均在B对应的直线上）。

接下来，为了量化方便和第二次S变换，在PC坐标系下建立一个笛卡尔坐标系U-V（绿色的坐标轴）。将所有的点和直线用U-V坐标表示，于是便有了S变换的表达式：线→点，点→线

这里使用了齐次坐标（x,y,w)。[]代表的一个点，()代表一条直线，d为平行坐标轴间距。

同理可得级联霍夫变换CHT的变换公式为：线→线，点→点

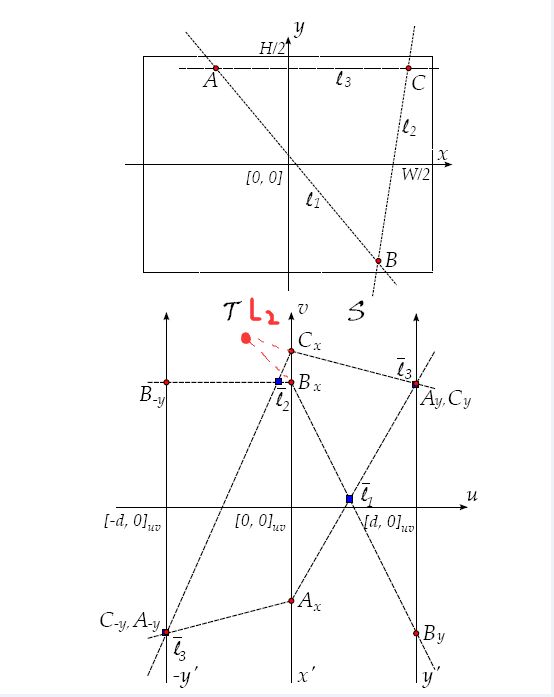
这时应该注意到，前面图中的直线都是斜率小于零的，这时就会发现一个问题，斜率大于零的直线在S空间是没办法表示的，如下图：

如图中的直线L2，在线上有B、C两个点，对应到S空间里是BxBy和CxCy两条直线，但它们的交点并不在S空间内。因此需要引入一个T空间，它只是位于-d的位置，并且方向与Y‘相反。有了T空间以后，L2便能在我们定义的T空间内表达了。因此，S和T空间可以定义X-Y坐标系下的所有直线。T变换的公式如下：

在清楚了S变换和T变换之后，CHT的公式便可得到，例如点→点的公式如下：

二、检测VanishingPoints：

原X-Y坐标系是一个无限大的空间，但经过CHT变换后，无限大的空间变到了一个有限的菱形空间里（diamond space）

并且笛卡尔坐标系X-Y和菱形空间的坐标系有如下的象限对应关系：

既然有上述的对应关系，那么X-Y坐标系下的经过三个象限的一条直线，经过CHT变换后到菱形空间后，就会成为三段折线：

并且这条折线可以由4个端点唯一确定，如下（()代表X-Y空间的一条直线，[ ]代表点）：

sgn代表这个表达式的符号（1，-1），需要注意的是当a或b等于0时，表达式的乘积会等于0，这时令对应的sgn=1即可。

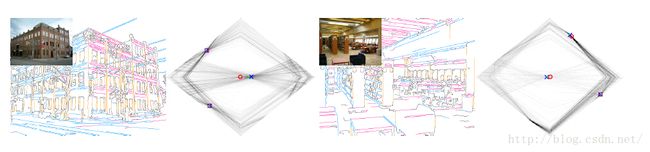
例如下面四条直线变换到菱形空间的情况，并且两个VP点也能在图中找出：

 

VP的坐标可以通过对整个菱形空间进行栅格化，因为VP点是同一方向的所有平行直线的交点，该点的权值最大，所以可以通过voting的方式找到VP点。如果有多个VP点，可以在找到一个之后，对所有该方向的线进行删除，再寻找下一个VP点，直到找完所求的所有VP点。得到VP点的坐标后，可以通过一个简单的公式即可得到原X-Y坐标系下VP点的坐标，公式如下（下表o代表original即原X-Y坐标系，下表d代表diamond即菱形空间坐标系）：

三、总结：

以上就是通过基于PC坐标系参数化的CHT变换来寻找消失点的思路，这个方法神奇的地方就在于通过一个简单的线性变换就把原本无限大的空间变到了一个有限的空间。这就方便了我们量化整个空间，使用Voting的方式找出VP点。

这种方法对检测自然图像中的消失点效果不错，此外，对于已知有正交消失点的图像，作者还利用了这一先验知识来优化最终的检测结果。

这里有作者的paper原文以及matlab测试代码：paper&code