Trie树(含实现代码)

Trie树系列

• Trie字典树
• 压缩的Trie
• 后缀树Suffix tree

Trie是通过对字符串进行预先处理，达到加快搜索速度的算法。即把文本中的字符串转换为树结构，搜索字符串的速度提高。

---

 

 

Trie树

 

Trie这个术语来自于retrieval。检索的意思。

Tire树，又叫字典树，前缀树，单词查找树或键树。从名字来看，就能大概了解它的用途了。专门用于处理字符串匹配的数据结构，用来解决在一组字符串集合中快速查找某个字符串的问题。

它是一种有序树，多叉树，用于保存关联数组，关键字通常是字符串，但是它不直接存在于某个节点，而是存在于一条路径上。

因为一个节点的所有子节点都有共同的关键字，所以Trie树也叫做前缀树(Prefix Tree)。

例子：

 

上图是一棵Trie树，表示了关键字集合{“a”, “to”, “tea”, “ted”, “ten”, “i”, “in”, “inn”} 

从中可看出特点：

• 根节点不包含字符，即空字符。根节点外的每个子节点都有一个字符。
• 从根节点到某一个节点，路径上经过的字符连接起来，为该节点对应的字符串。
• 每个节点的子节点包含的字符互不相同。

通常在实现的时候，会在节点结构中设置一个标志，用来标记该结点处是否构成一个单词（关键字）。

---

 

核心思想：

利用字符串的公共前缀来减少无谓的字符串比较以达到提高查询效率的目的。

 

优点：

1. 插入和查询效率是O(m), m是字符串的字符数量。
2. Trie树中不同的关键字不会产生冲突。
3. Trie树不用求 hash 值，对短字符串有更快的速度。通常，求hash值也是需要遍历字符串的。
4. Trie树可以对关键字按字典序排序。

缺点：

1. 当 hash 函数很好时，Trie树的查找效率会低于哈希搜索。（不理解⚠️）

2. 空间消耗比较大。

 

---

Trie树的应用：

具体来说就是经常用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：最大限度地减少无谓的字符串比较，查询效率比哈希表高。

1.前缀匹配：

trie树常用于搜索提示。如当输入一个网址，可以自动搜索出可能的选择。当没有完全匹配的搜索结果，可以返回前缀最相似的可能。

还有如各种通讯录的自动补全功能等。

 

2字符串检索：

给出 N 个单词组成的熟词表，以及一篇全用小写英文书写的文章，按最早出现的顺序写出所有不在熟词表中的生词。

 

检索/查询功能是Trie树最原始的功能。给定一组字符串，查找某个字符串是否出现过，思路就是从根节点开始一个一个字符进行比较：

• 如果沿路比较，发现不同的字符，则表示该字符串在集合中不存在。
• 如果所有的字符全部比较完并且全部相同，还需判断最后一个节点的标志位（标记该节点是否代表一个关键字）。

3.词频统计：

虽然也可以用hash做，但是如果内存空间有限，就不行了。这里我们就可以用trie树来压缩下空间，因为公共前缀都是用一个节点保存的。

 

Trie树的局限性

如前文所讲，Trie的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

所谓的空间，是指每一个字符都要单独开辟一块储存空间，并使用指针指向它。因此空间开销大增。但这种结构带来了查询效率的提升，这就是空间换时间。

 

假设字符的种数有m个，有若干个长度为n的字符串构成了一个 Trie树 ，则每个节点的出度为 m（即每个节点的可能子节点数量为m），Trie树 的高度为n。很明显我们浪费了大量的空间来存储字符，此时Trie树的最坏空间复杂度为O(m^n)。也正由于每个节点的出度为m，所以我们能够沿着树的一个个分支高效的向下逐个字符的查询，而不是遍历所有的字符串来查询，此时Trie树的最坏时间复杂度为O(n)。

这正是空间换时间的体现，也是利用公共前缀降低查询时间开销的体现。

 

Trie树在空间上也是有优化策略的，比如对部分前缀或者后缀进行压缩，这样以来能够节省不必要的指针存储，这种实现需要更复杂的编码来支持。

 

Ruby实现的T树的插入，查找，和删除

代码使用的是数组来存储所有的子节点。

最新版本的代码见git

class T_tree
  attr_accessor :root

  def initialize
    @root = Trie_node.new()
    @root.children = []  #用于储存根节点的孩子节点
  end

  #词频统计，给空树插入一个单词，如果第2次又插入这个词，就会发现重复，然后count+1.
  def insert(next_child = @root, word)
    # 判断传入的字符串的第一个字母是否存在于当前节点的孩子内。
    exist_node = try(next_child.children, word[0])
    if exist_node
      # 继续判断node[1]是否在exist_node节点的儿子们中：
      if word.size == 1  #如果待插字符串只剩最后一个字母，证明这个单词没有后续了。
        # 词出现频率统计：
        exist_node.count += 1 #因为当前节点是一个词的最后的字符，所以加1.
        return
      else
        # 重复使用insert方法（），传入剩下的字符
        insert(exist_node, word.slice(1..-1))
      end
    else
      # "当前节点的孩子中不包括#{word[0]},插入#{word}"
      i = 0
      size = word.size
      while  i < size
        next_child =  _insert(next_child, word[i])
        # 词频统计：在插入的单词的最后生成的叶节点中：count+1
        if i == (size -1)
          next_child.count += 1
        end
        i += 1
      end
    end
  end

  # 字符串检索：查找单词是否已经存在于树中，如果不存在则打印
  def find(word)
    if _find(word)
      puts "#{word}存在于库中"
    else
      puts "#{word}不存在"
    end
  end

  def delete(word)
    if _find(word)
      puts "#{word}存在于库中, 是否删除它？ > true"
      if _delete(word) == true
        puts "删除成功"
      else
        puts "不能删除前缀词"
      end
    else
      puts "#{word}不存在"
    end
  end

  private
    def _find(next_child = @root, word)
      exist_node = try(next_child.children, word[0])
      if exist_node
        # 只剩最后一个字母
        if word.size == 1
          return true
        else
          # word还有多个字母，继续查找比较。
          return _find(exist_node, word.slice(1..-1))
        end
      else
        return false
      end
    end

    def _delete(next_child = @root, word)
      exist_node = try(next_child.children, word[0])
      # 已经比较完最后一个字母
      if word.size == 1
        #如果当前节点有儿子，则不能删除它。
        if exist_node.children.size != 0
          #"不能删除前缀单词！"
          return false
        else
          exist_node = nil
          return true
        end
      else
        # word还有多个字母，继续查找比较。
        if _delete(exist_node, word.slice(1..-1)) == true
          exist_node = nil
        else
          return false
        end
      end
    end

    def try(childen, x)
      childen.each do |c|
        if c.node == x
          return c
        end
      end
      return false
    end

    def _insert(node, letter)
      new_node = Trie_node.new(letter)
      node.children << new_node
      return new_node
    end
end

class Trie_node
  attr_accessor :count, :node, :children

  def initialize(node = "")
    @node = node
    @count = 0 #记录从根节点到这个节点的，共走了多少次。
    @children = []
  end
end

 

摘录和参考：

https://juejin.im/post/5c2c096251882579717db3d2

https://blog.csdn.net/lisonglisonglisong/article/details/45584721

https://en.wikipedia.org/wiki/Trie

https://blog.csdn.net/StevenKyleLee/article/details/38343985

https://blog.csdn.net/johnny901114/article/details/80711441 推荐?。

 

---

 

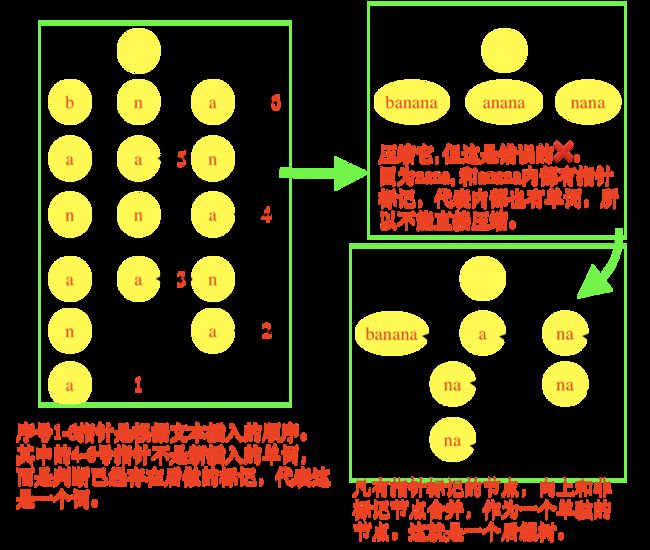
压缩字典树

参考：https://sqh.me/tech/search-in-large-string-data-by-using-trie-and-compressed-trie/

 

由于使用树+指针实现Trie树非常耗用内存，所以可以将原始Trie树进行压缩，即只有单个子节点的节点可以合并成一个节点（一个孤立的string）。

the space of complexity空间复杂度，就可以从O(m*n)降低到O(n)。

 

---

 

 

Suffix Trees

后缀树提出的目的是用来支持有效的字符串匹配和查询，例如上面的问题。后缀树（Suffix tree）是一种数据结构，能快速解决很多关于字符串的问题。后缀树的概念最早由Weiner 于1973年提出，既而由McCreight 在1976年和Ukkonen在1992年和1995年加以改进完善。

 

参考这篇文章https://www.cnblogs.com/gaochundong/p/suffix_tree.html。

 

字符串匹配算法

理解3点：

• 对字符串匹配的算法分为两个步骤：Preprocessing和Matching。算法的总运行时间是2者之和。
• 字典树系列：是对文本text进行预先处理Preprocessing，即把文本储存在树结构内。
• 除此之外，有对匹配Matching进行预先处理的算法: KMP字符串匹配算法，Boyer-Moore字符串匹配算法。

 

性质

• 文本长度为n, 储存所有的n(n-1)/2个后缀需要 O(n)空间
• d为字符集的长度，构建后缀树的时间是：O(d*n)
• 模式的长度m, 对其查询时间为O(d*m)

构建后缀树，首先是后缀树是压缩树，然后后缀树中的关键词为后缀：

1. 根据文本生成所有后缀的集合
2. 将每个后缀作为一个单独的关键词，构成压缩的字典树。

例如banana这个词，包括6个后缀：

banana
anana
nana
ana
na
a

构成字典树，并压缩后是： 

 

 

 

 

 

 

 

 

 

 

 

 

转载于:https://www.cnblogs.com/chentianwei/p/11598410.html