【调参17】如何使用贪婪逐层预训练分析不同层数对深度神经网络的影响

---

---

1. 贪婪逐层预训练策略

训练具有多个层次的深度神经网络具有挑战性。随着隐藏层数量的增加，传播回先前层的误差信息数量将大量减少。这意味着，靠近输出层的隐藏层中的权重会正常更新，而靠近输入层的隐藏层中的权重会极少更新或根本没有更新。通常，此问题阻止了非常深的神经网络训练，称为梯度消失问题（vanishing gradient problem）。

最初，开发更深的神经网络模型的一个重要里程碑是贪婪的逐层预训练技术，通常简称为预训练（pretraining）。

预训练涉及到先后向模型添加新的隐藏层并进行重新拟合，以使新添加的模型可以从现有的隐藏层中学习输入，而同时又要保持现有隐藏层的权重不变。模型一次添加一层进行训练的技术称为逐层（layer-wise）。

该技术之所以称为贪婪（greedy），是因为采用分段或分层的方法来解决训练深度网络的较难问题。贪婪算法将一个问题分解为多个部分，然后独立解决每个部分的最佳版本。不幸的是，不能保证将各个最佳部分组合在一起就可以得出最佳的完整解决方案。

预训练基于这样的假设：较浅的网络更容易训练，并进行分层的训练过程，而始终只适合于浅层模型。

1.1 预训练的好处

• 简化训练过程。
• 促进建立更深层的网络。
• 用作权重初始化方案。
• 可能获得更低的泛化误差。

1.2 预训练的方法

预训练有两种主要方法：他们是：

• 有监督的贪婪逐层预训练；
• 无监督的贪婪逐层预训练。

通常使用 预训练（pretraining） 一词不仅指预训练阶段本身，而且指结合了预训练阶段和监督学习阶段。监督学习阶段可能涉及在预训练阶段之上训练一个简单的分类器，或者可能涉及对在预训练阶段学习的整个网络进行有监督的微调。

当有大量未标记的样本可用于初始化模型，然后使用数量更少的样本来微调监督模型权重时，无监督预训练可能是适当的。

尽管先前层中的权重保持恒定，但通常在添加最后一层之后最后微调网络中的所有权重。这将预训练视为权重初始化方法的一种。它利用了这样的思想，即为深度神经网络选择初始参数可能会对模型产生显着的正则化影响（并且在较小程度上可以改善优化）。

贪婪的逐层预训练是深度学习历史中的一个重要里程碑，它允许早期开发具有比以前更多的隐藏层的网络。如今，无监督的预训练已基本被抛弃，除了在自然语言处理领域。例如，最佳实践是对文本数据使用无监督预训练，以便通过word2vec提供更丰富的单词及其相互关系的分布式表示（distributed representation）。

今天，现在知道训练全连接的深度架构不需要贪婪的逐层预训练，使用现代方法（例如更好的激活函数，权重初始化，梯度下降变体和正则化方法）可能会实现更好的性能；但是无监督的预训练方法是第一个成功的方法。

---

2. 多分类问题

使用一个小的多类分类问题作为基础来证明贪婪的逐层预训练对模型性能的影响。

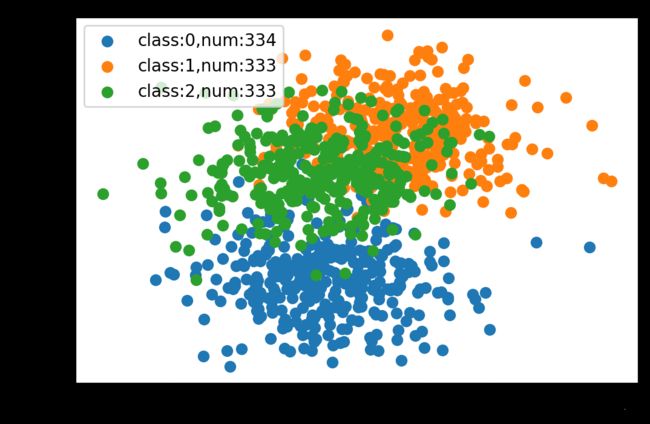
scikit-learn类提供了 make_blobs()函数 ，该函数可用于创建具有指定数量的样本，输入变量，类以及一个类中样本的方差的多类分类问题。

使用两个输入变量（代表点的x和y坐标）和每个组中点的标准偏差2.0进行配置。使用相同的随机状态（用于伪随机数生成器的种子）来确保始终获得相同的数据点。

---

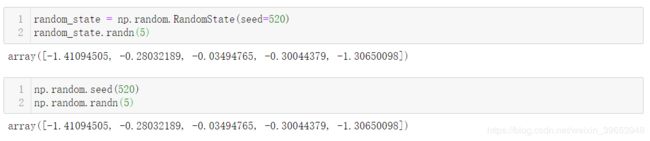
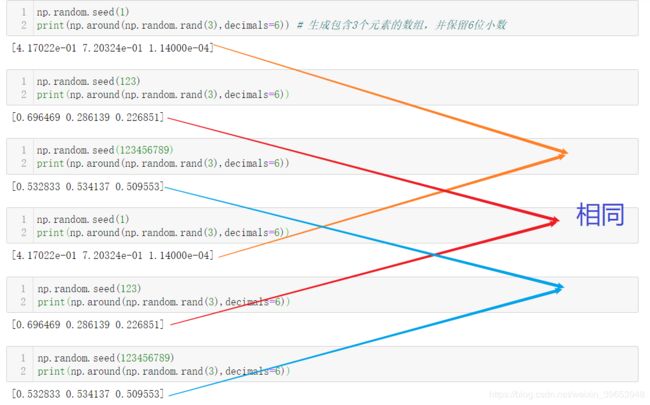
这里班门弄斧一下，一开始对随机种子也有很大的疑惑，比如np.random.seed(2) 中的“2”，一直以为是生成随机数的个数或者重复次数，其实这个理解是错误的；这个值表示随机数生成的初始状态或者说是第一个随机数生成的标准，相当于提供了随机数生成规则（或者说预定义的伪随机数生成公式）中的初始值，只要这个种子值相同，生成的随机序列就是相同的。看一下简单的示例说明问题。

关于 random.seed()，numpy的主要贡献者 Robert Kern 建议不要使用，而是使用 random.RandomState() 来代替，通过stack overflow 回答，总结主要原因如下：

• 如果部署设置随机种子的代码，则会引入安全漏洞。
• RandomState()实例基本上使用计算机内部时钟来设置种子。
  
  详细讨论，请查看文末最后两篇参考文章。

---

创建虚拟样本集完整代码：

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
from numpy import where

# 生成二维平面中的三类样本点；
# 其中X的shape为（1000,2）,“2”代表样本点的横纵轴坐标；y的shape为（1000，）表示样本标签。
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)

# 设置绘图的像素值为200
plt.figure(dpi=200)

# 统计各类样本的个数
samples_num = {}

# 绘制各类样本的散点图
for class_value in range(3):
    # s通过样本标签找出各类样本对应的索引
    row_ix = where(y == class_value) # 返回元组
    # 统计各类样本数量
    samples_num[class_value] = row_ix[0].shape[0]
    # 使用不同颜色绘制散点图
    plt.scatter(X[row_ix, 0], X[row_ix, 1], label=f'class:{class_value},num:{samples_num[class_value]}')

plt.legend()
plt.show()

输出：

---

2.1 有监督的 贪婪逐层预训练

为上述创建的多分类问题建立一个深层的多层感知器（MLP）模型来探讨网络层数的影响。

---

2.1.1 准备数据

首先，创建1000个样本，并将它们均匀地分为训练和测试数据集。

from tensorflow.keras.utils import to_categorical
def prepare_data():
    # 生成样本
    X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
    # one-hot编码
    y = to_categorical(y) 
    # 训练集、验证集（测试集）划分
    n_train = 500
    trainX, testX = X[:n_train, :], X[n_train:, :]
    trainy, testy = y[:n_train], y[n_train:]
    return trainX, testX, trainy, testy

---

2.1.2 定义模型

其次，创建基本的MLP模型，期望数据集中的两个输入变量有两个输入，包含10个节点，使用relu激活函数，并配置何恺明权重初始化。输出层具有三个节点，使用softmax激活函数以预测三个类别中每个类别的概率。使用随机梯度下降进行拟合，默认学习率为0.01，动量值为0.9。使用交叉熵损失函数进行优化。

from tensorflow.keras.layers import Dense
from tensorflow.keras.models import Sequential
from tensorflow.keras.optimizers import SGD

def get_base_model(trainX, trainy):
    # 模型定义
    model = Sequential()
    model.add(Dense(10, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
    model.add(Dense(3, activation='softmax'))
    # 模型编译
    opt = SGD(lr=0.01, momentum=0.9)
    model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
    # 模型训练
    model.fit(trainX, trainy, epochs=100, verbose=0)
    return model

---

2.1.3 评估模型

然后，定义模型评估方法。下面自定义的evaluate_model() 函数将训练集和测试集以及模型作为参数，并返回两个数据集的准确性。

def evaluate_model(model, trainX, testX, trainy, testy):
    _, train_acc = model.evaluate(trainX, trainy, verbose=0)
    _, test_acc = model.evaluate(testX, testy, verbose=0)
    return train_acc, test_acc

---

2.1.4 贪婪逐层预训练配置

现在，配置贪婪逐层预训练。需要一个可以添加新的隐藏层并重新训练模型，但仅更新新添加的层和输出层中的权重的函数。

首先，存储当前输出层，包括其配置和当前的权重。

output_layer = model.layers[-1]

其次，将其从模型中删除。

model.pop()

然后，将模型中的所有其余层标记为不可训练，这意味着当再次调用 fit() 函数时，它们的权重无法更新。

for layer in model.layers:
	layer.trainable = False

然后，添加一个新的隐藏层，其配置与基本模型中添加的第一个隐藏层相同。

model.add(Dense(10, activation='relu', kernel_initializer='he_uniform'))

然后，可以添加输出层，并将模型重新拟合到训练数据集上。

model.add(output_layer)
model.fit(trainX, trainy, epochs=100, verbose=0)

将其封装为add_layer()函数，方便调用。

def add_layer(model, trainX, trainy):
    # 保留输出层，以便添加新的隐藏层
    output_layer = model.layers[-1]
    model.pop()
    
    # 将之前的层设置为不可训练，以保证权重不更新
    for layer in model.layers:
        layer.trainable = False
        
    # 添加隐藏层，其配置与基本模型的第一层相同
    model.add(Dense(10, activation='relu', kernel_initializer='he_uniform'))
    model.add(output_layer)
    
    # 训练模型
    model.fit(trainX, trainy, epochs=100, verbose=0)

最后，根据希望添加到模型中的层数来重复调用此函数。对于模型中的层数，训练和测试准确率存储在字典中。

n_layers = 10
for i in range(n_layers):
    # 添加隐藏层
    add_layer(model, trainX, trainy)
    # 评估模型
    train_acc, test_acc = evaluate_model(model, trainX, testX, trainy, testy)
    print('> layers=%d, train=%.3f, test=%.3f' % (len(model.layers), train_acc, test_acc))
    # 将准确率存储到字典，方便绘图
    scores[len(model.layers)] = (train_acc, test_acc)

plt.plot(list(scores.keys()), [scores[k][0] for k in scores.keys()], label='train', marker='.')
plt.plot(list(scores.keys()), [scores[k][1] for k in scores.keys()], label='test', marker='.')
plt.legend()
plt.show()

2.1.5 完整代码

from sklearn.datasets import make_blobs
from tensorflow.keras.layers import Dense
from tensorflow.keras.models import Sequential
from tensorflow.keras.optimizers import SGD
from tensorflow.keras.utils import to_categorical
import matplotlib.pyplot as plt
plt.rcParams['figure.dpi'] = 200

# 1.准备数据
def prepare_data():
    # 生成样本
    X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
    # one-hot编码
    y = to_categorical(y) # tf.keras.utils.to_categorical
    # 训练集、验证集（测试集）划分
    n_train = 500
    trainX, testX = X[:n_train, :], X[n_train:, :]
    trainy, testy = y[:n_train], y[n_train:]
    return trainX, testX, trainy, testy

# 2.定义模型
def get_base_model(trainX, trainy):
    # 模型定义
    model = Sequential()
    model.add(Dense(10, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
    model.add(Dense(3, activation='softmax'))
    # 模型编译
    opt = SGD(lr=0.01, momentum=0.9)
    model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
    # 模型训练
    model.fit(trainX, trainy, epochs=100, verbose=0)
    return model

# 3.评估模型
def evaluate_model(model, trainX, testX, trainy, testy):
    _, train_acc = model.evaluate(trainX, trainy, verbose=0)
    _, test_acc = model.evaluate(testX, testy, verbose=0)
    return train_acc, test_acc

# 4.贪婪逐层预训练配置
def add_layer(model, trainX, trainy):
    # 保留输出层，以便添加新的隐藏层
    output_layer = model.layers[-1]
    model.pop()
    
    # 将之前的层设置为不可训练，以保证权重不更新
    for layer in model.layers:
        layer.trainable = False
        
    # 添加隐藏层，其配置与基本模型的第一层相同
    model.add(Dense(10, activation='relu', kernel_initializer='he_uniform'))
    model.add(output_layer)
    
    # 训练模型
    model.fit(trainX, trainy, epochs=100, verbose=0)
    
# 准备数据
trainX, testX, trainy, testy = prepare_data()
# 基本模型
model = get_base_model(trainX, trainy)
# 创建字典，用于保存不同隐藏层模型的准确率
scores = {}
# 训练与评估
train_acc, test_acc = evaluate_model(model, trainX, testX, trainy, testy)
# 打印准确率
print('> layers=%d, train=%.3f, test=%.3f' % (len(model.layers), train_acc, test_acc))
# 保存准确率
scores[len(model.layers)] = (train_acc, test_acc)

n_layers = 10

for i in range(n_layers):
    # 添加隐藏层
    add_layer(model, trainX, trainy)
    # 评估模型
    train_acc, test_acc = evaluate_model(model, trainX, testX, trainy, testy)
    print('> layers=%d, train=%.3f, test=%.3f' % (len(model.layers), train_acc, test_acc))
    # 将准确率存储到字典，方便绘图
    scores[len(model.layers)] = (train_acc, test_acc)

plt.plot(list(scores.keys()), [scores[k][0] for k in scores.keys()], label='train', marker='.')
plt.plot(list(scores.keys()), [scores[k][1] for k in scores.keys()], label='test', marker='.')
plt.legend()
plt.show()

输出：

> layers=2, train=0.814, test=0.834
> layers=3, train=0.834, test=0.828
> layers=4, train=0.846, test=0.830
> layers=5, train=0.846, test=0.828
> layers=6, train=0.836, test=0.826
> layers=7, train=0.846, test=0.824
> layers=8, train=0.840, test=0.816
> layers=9, train=0.836, test=0.826
> layers=10, train=0.846, test=0.826
> layers=11, train=0.844, test=0.826
> layers=12, train=0.840, test=0.820

训练数据集上模型的准确率有所提高，可能是因为它开始过拟合数据；由于过拟合，测试数据集上的分类准确率下降。

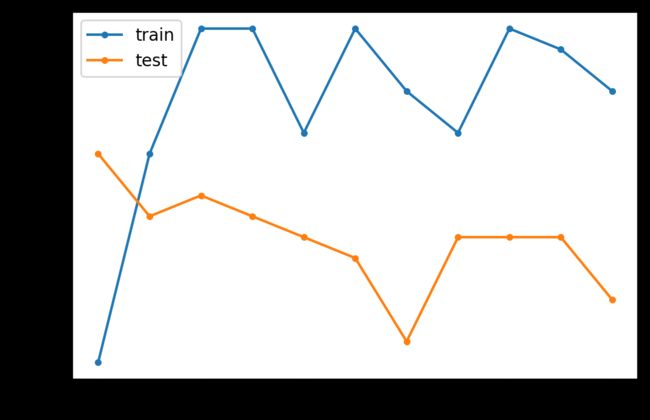
在这种情况下，该图表明训练数据集略有过拟合，但是在添加了七个层之后，也许测试集的性能更好。

---

2.2 无监督的 贪婪逐层预训练

基本的模型如下：

def base_autoencoder(trainX, testX):
    model = Sequential()
    model.add(Dense(10, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
    
    model.add(Dense(2, activation='linear'))
    model.compile(loss='mse', optimizer=SGD(lr=0.01, momentum=0.9))
    
    model.fit(trainX, trainX, epochs=100, verbose=0)
    train_mse = model.evaluate(trainX, trainX, verbose=0)
    test_mse = model.evaluate(testX, testX, verbose=0)
    print('> reconstruction error train=%.3f, test=%.3f' % (train_mse, test_mse))
    return model

其它部分基本不变。

---

参考：
https://machinelearningmastery.com/greedy-layer-wise-pretraining-tutorial/
伪随机数生成器：https://baijiahao.baidu.com/s?id=1622255193902414898&wfr=spider&for=pc
np.random.seed() 理解，关注评论区可能会醍醐灌顶：https://blog.csdn.net/linzch3/article/details/58220569
random.seed() :What does it do?：https://stackoverflow.com/questions/22639587/random-seed-what-does-it-do
random.RandomState()：https://stackoverflow.com/questions/5836335/consistently-create-same-random-numpy-array/5837352#5837352
https://stackoverflow.com/questions/37224116/difference-between-randomstate-and-seed-in-numpy