前言
一部分有工作经验的老司机对数据结构是很熟悉了,而一部分刚参加工作或者刚入行的人对数据结构是略懂一二甚至是感到陌生,希望本篇文章可以让老司机更熟悉数据结构的实现,不懂数据结构的小白对数据结构的实现有一定的了解。
本系列文章使用多种语言实现常用的数据结构,包括目前使用最多的 Java,21 世纪兴起的 Go,前端领域的 JavaScript,目的是尽可能的让更多的人能够看的懂、看的明白。整体上采用文字、图和代码的方式进行介绍,代码默认使用 Go 语言版本,其它语言请参考完整的源代码,对应的源代码见下文。
所有已经更新的内容在 Github 上,如果对你有帮助请给个 star,谢谢 \ (•◡•) /,你的肯定是我继续更新的动力 ☺。
栈(stack)
各种语言实现代码:Go Java JavaScript
默认使用 Go 语言实现。
简介
栈和队列一样也是一种特殊的线性表。它只能在表尾进行插入和删除操作。在进行插入和删除操作的一端被称为栈顶,另一端称为栈底。向一个栈放入新元素称为进栈、入栈或压栈,从一个栈取出元素称为出栈或退栈。每一个新元素都会放在之前放入的元素之上,删除时会删除最新的元素,所以栈有先进后出(FILO—first in last out)的特点。
实现
使用数组来实现栈。
- 定义数组用来存储栈元素
- 定义栈中元素最大大小 maxSize
- 定义栈顶,初始值为 -1
- 入栈方法 push
- 出栈方法 pop
定义结构体和创建结构体的函数:
type Stack struct {
array []string // 存放栈元素的切片(数组无法使用变量来定义长度)
maxSize int // 最大栈元素大小
top int // 栈顶
}
func NewStack(size int) *Stack {
return &Stack {
array: make([]string, size),
maxSize: size,
top: -1, // 初始化为 -1
}
}入栈方法:
func (s *Stack) Push(elem string) error {
// 判断栈是否已满
if s.top == s.maxSize - 1 {
return errors.New("stack is full")
}
s.top++ // 栈顶加 1
s.array[s.top] = elem
return nil
}出栈方法:
func (s *Stack) Pop() (string, error) {
if s.top == -1 {
return "", errors.New("stack is empty")
}
elem := s.array[s.top]
s.top-- // 栈顶减 1
return elem, nil
}为了方便查看输出结果,重新定义 String 方法:
// 重新定义 String 方法,方便输出
func (s *Stack) String() string {
str := "["
for i := s.top; i >= 0; i-- {
str += s.array[i] + " "
}
str += "]"
return str
}测试代码:
func main() {
// 创建一个栈
stack := array.NewStack(3)
// 入栈
_ = stack.Push("one")
_ = stack.Push("two")
_ = stack.Push("three")
// 栈满,无法入栈
err := stack.Push("four")
if err != nil {
fmt.Println(err)
}
fmt.Println(stack)
elem1, _ := stack.Pop()
elem2, _ := stack.Pop()
elem3, _ := stack.Pop()
fmt.Println("出栈:", elem1)
fmt.Println("出栈:", elem2)
fmt.Println("出栈:", elem3)
// 栈空无法出栈
_, err = stack.Pop()
if err != nil {
fmt.Println(err)
}
fmt.Println(stack)
}运行输出:
stack is full
[three two one ]
出栈: three
出栈: two
出栈: one
stack is empty
[]综合计算器
使用栈实现一个加减乘除的计算器。假设一个字符串为 3+5*3-6,计算该表达式的值。
思路分析
-
定义两个栈,一个为数栈,一个为符号栈。
-
截取字符串(需要考虑多位数),判断是否为数字,如果为数字,将字符串压入数栈,如果为运算符压入符号栈。
-
压入符号栈前判断符号栈是否为空。
-
如果符号栈为空,直接入栈。
-
如果符号栈不为空,从符号栈中试探出一个符号,判断优先级。
-
如果当前将要入栈的符号优先级小于或等于从符号栈中取出来的优先级
从数栈中弹出两个数,再从符号栈中弹出一个符号,进行运算,将运算
结果压入数栈,再将要入栈的符号入栈。否则将当前符号直接入栈。
-
-
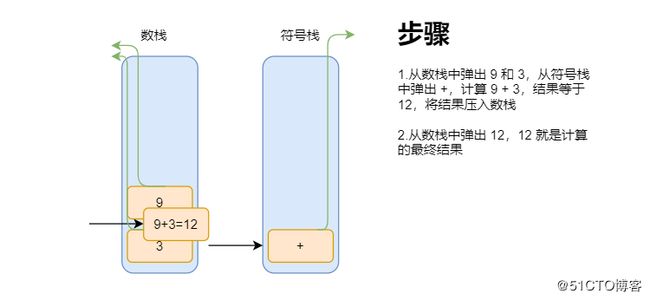
不断的从操作符栈中取出一个符号,从数栈中取出两个数,进行计算,将计算结果压入数栈,
当符号栈为空时跳出循环,此时数栈中的最后一个元素就是最终的计算结果。
画图分析
代码实现
在之前实现的栈结构体中增加两个方法:
// 判断栈是否为空
func (s *Stack) IsEmpty() bool {
return s.top == -1
}
// 窥视栈顶元素
func (s *Stack) Peek() string {
if s.IsEmpty() {
return ""
}
return s.array[s.top]
}定义操作符结构体,定义相关操作符对应的优先级和计算方法:
type Operation struct {
operation string
priority int
optFunc func(num1, num2 int) int
}
// 定义相关操作符对应的优先级和计算方法
var operations = map[string]Operation{
"+": {"+", 1, func(num1, num2 int) int {
return num1 + num2
}},
"-": {"-", 1, func(num1, num2 int) int {
return num1 - num2
}},
"*": {"*", 2, func(num1, num2 int) int {
return num1 * num2
}},
"/": {"/", 2, func(num1, num2 int) int {
return num1 / num2
}},
}定义计算器结构体和相关方法:
type Calculator struct {
numStack *array.Stack // 数栈
operationStack *array.Stack // 符号栈
}
func NewCalculator() *Calculator {
numStack := array.NewStack(10)
operationStack := array.NewStack(10)
return &Calculator{numStack: numStack, operationStack: operationStack}
}
// 判断是否是操作符号
func (cal *Calculator) isOperation(opt string) bool {
_, ok := operations[opt]
return ok
}
// 判断是否为数字
func (cal *Calculator) isNum(char string) bool {
matched, _ := regexp.MatchString("\\d+", char)
return matched
}
// 计算操作符的优先级
func (cal *Calculator) priority(opt1, opt2 string) int {
operation1, ok1 := operations[opt1]
operation2, ok2 := operations[opt2]
if ok1 && ok2 {
return operation1.priority - operation2.priority
} else {
panic(fmt.Sprintf("请检查运算符: %s, %s\n", opt1, opt2))
}
}
// 计算结果
func (cal *Calculator) calculateNum(num1, num2 int, opt string) int {
optFunc := operations[opt].optFunc
if opt == "-" || opt == "/" {
// 因为出栈后两数的位置颠倒,需交换两个数的位置
num1, num2 = num2, num1
}
return optFunc(num1, num2)
}
func (cal *Calculator) calculateNumFromStack() int {
// 从数栈中弹出两个数,从符号栈中弹出一个符号
numStr1, _ := cal.numStack.Pop()
numStr2, _ := cal.numStack.Pop()
opt, _ := cal.operationStack.Pop()
num1, _ := strconv.Atoi(numStr1)
num2, _ := strconv.Atoi(numStr2)
// 计算值
return cal.calculateNum(num1, num2, opt)
}计算表达式的核心方法如下:
func (cal *Calculator) Calculate(expression string) {
if expression == "" {
return
}
var index int
var number string
for index < len(expression) {
char := expression[index : index+1]
// 判断是否为符号
if cal.isOperation(char) {
// 判断符号栈是否为空
if cal.operationStack.IsEmpty() {
// 压入符号栈
_ = cal.operationStack.Push(char)
} else {
// 符号栈不为空,判断优先级
opt := cal.operationStack.Peek()
// char 优先级小于等于 elem
if cal.priority(char, opt) <= 0 {
// 计算值
result := cal.calculateNumFromStack()
// 将计算结果入数栈
_ = cal.numStack.Push(strconv.Itoa(result))
}
// 将当前操作符入符号栈
_ = cal.operationStack.Push(char)
}
} else if cal.isNum(char) {
// 向后面再取一位判断是否为数字
if index < len(expression)-1 && cal.isNum(expression[index+1:index+2]) {
number += char
index++
continue
}
// 压入数栈
_ = cal.numStack.Push(number + char)
number = ""
} else {
panic("无法识别的字符:" + char)
}
index++
}
// 全部数和符号都压入对应的栈后,取出计算
// 符号栈为空,跳出循环
for !cal.operationStack.IsEmpty() {
// 计算值
result := cal.calculateNumFromStack()
// 将计算结果入数栈
_ = cal.numStack.Push(strconv.Itoa(result))
}
// 弹出最终结果
result, _ := cal.numStack.Pop()
fmt.Printf("表达式执行结果: %s=%s\n", expression, result)
}测试代码:
func main() {
calculator := NewCalculator()
calculator.Calculate("3+5*3-6")
calculator.Calculate("30+5*3-6")
calculator.Calculate("130+5*3-6")
}输出:
表达式执行结果: 3+5*3-6=12
表达式执行结果: 30+5*3-6=39
表达式执行结果: 130+5*3-6=139逆波兰计算器
简介
逆波兰计算器使用逆波兰表达式来计算表达式的值。逆波兰表达式也叫后缀表达式,后缀表达式指的是运算符写在操作数之后,比如 12+,它是计算机比较容易计算的一种表达式,因为计算机采用栈结构,执行先进后出的顺序。与之对应的有前缀表达式,中缀表达式,我们人一般识比较容易理解的是中缀表达式,比如 3+5*3-6 就属于中缀表达式。
后缀表达式计算
假设一个后缀表达式为 353*+2-,计算出该后缀表达式的值。
思路分析:
- 循环读取每个字符,判断是否是数字。
- 如果是数字直接入栈。
- 如果是运算符,从栈中弹出两个数,计算表达式的值,将结果压入栈中。
步骤:
- 将 3,5,3 压入栈中。
- 读取到 * 时,从栈中弹出两个数,栈顶弹出一个数 3,次栈顶弹出一个数 5。
- 计算 3 * 5,结果等于 15,将结果压入栈中。
- 读取到 + 时,从栈中弹出 15 和 3。
- 计算 15 + 3,结果等于 18,将 18 压入栈中。
- 将 2 压入栈中。
- 读取到 - ,从栈中弹出 2 和 18。后一个数减去前一个数即 18 - 2。
- 计算 18 - 2,结果等于 16,将结果压入栈中。
- 循环结束后,栈中的 16 就是表达式的值。
代码实现
定义操作符,计算两个数,判断是否为数值等方法:
type Opt struct {
operation string
priority int
optFunc func(num1, num2 int) int
}
// 定义相关操作符对应的优先级和计算方法
var opts = map[string]Opt{
"+": {"+", 1, func(num1, num2 int) int {
return num1 + num2
}},
"-": {"-", 1, func(num1, num2 int) int {
return num1 - num2
}},
"*": {"*", 2, func(num1, num2 int) int {
return num1 * num2
}},
"/": {"/", 2, func(num1, num2 int) int {
return num1 / num2
}},
}
// 计算结果
func calculateNum(num1, num2 int, opt string) int {
optFunc := opts[opt].optFunc
if opt == "-" || opt == "/" {
// 因为出栈后两数的位置颠倒,需交换两个数的位置
num1, num2 = num2, num1
}
return optFunc(num1, num2)
}
func isNum(s string) bool {
matched, _ := regexp.MatchString("\\d+", s)
return matched
}计算后缀表达式的方法:
func calSuffixExpression(expr []string) int {
stack := array.NewStack(len(expr))
for _, str := range expr {
if isNum(str) {
_ = stack.Push(str)
continue
}
_, ok := opts[str]
if !ok {
panic("无效的运算符:" + str)
}
// 计算
numStr1, _ := stack.Pop()
numStr2, _ := stack.Pop()
num1, _ := strconv.Atoi(numStr1)
num2, _ := strconv.Atoi(numStr2)
result := calculateNum(num1, num2, str)
// 入栈
_ = stack.Push(strconv.Itoa(result))
}
elem, _ := stack.Pop()
result, _ := strconv.Atoi(elem)
return result
}测试代码如下:
func main() {
expr := "3 5 3 * + 2 -"
// 假设数和数或符号之间有空格
expressions := strings.Split(expr, " ")
result := calSuffixExpression(expressions)
fmt.Printf("后缀表达式 %s 的计算结果为:%d\n", expr, result)
}输出:
后缀表达式 3 5 3 * + 2 - 的计算结果为:16中缀转后缀表达式
将中缀表达式转换成后缀表达式,步骤如下:
- 初始化两个栈,一个运算符栈 stack1 和另一个储存中间结果的栈 stack2。
- 从左至右扫描中缀表达式。
- 遇到数字时,将其压入 stack2。
- 如果是 "(" 号直接压入 stack1。
- 如果是 ")" 号,依次弹出 stack1 中栈顶的元素,并压入 stack2 中,直到遇到 "(" 将这一对括号丢弃。
-
遇到运算符时,比较其与 stack1 栈顶运算符的优先级
- 如果 stack1 为空或栈顶运算符为左括号 "(",则直接将此运算符入栈。
- 如果优先级比栈顶运算符低或者相等,将 stack1 栈顶的运算符弹出并压入到 stack2 中,再次转到 6-1 步,与 stack1 中新的栈顶运算符相比较,最后将当前运算符压入 stack1。
- 重复 2 - 6,直到表达式末尾。
- 将 stack1 中剩余的运算符依次弹出并压入 stack2 中。
- 依次弹出 stack2 中的元素,将结果逆序就是转换后的后缀表达式。
代码实现
定义一个将字符串表达式转换成切片的函数:
func exprToSlice(expr string) []string {
var expressions []string
for i := 0; i < len(expr); i++ {
char := expr[i : i+1]
if isNum(char) {
// 向后面继续判断是否为数字
for i + 1 < len(expr) && isNum(expr[i+1:i+2]) {
char += expr[i+1:i+2]
i++
}
}
expressions = append(expressions, char)
}
return expressions
}判断两个操作符的优先级函数:
func priority(opt1, opt2 string) int {
operation1, ok1 := opts[opt1]
operation2, ok2 := opts[opt2]
if ok1 && ok2 {
return operation1.priority - operation2.priority
} else {
panic(fmt.Sprintf("请检查运算符: %s, %s\n", opt1, opt2))
}
}接下来就是关键的中缀表达式转后缀表达式函数:
func infixToSuffix(infix []string) []string {
// 初始化两个栈,一个运算符栈 stack1 和另一个储存中间结果的栈 stack2
stack := array.NewStack(len(infix))
var suffixes []string // 由于中间结果栈不需要弹出元素,可以使用数组来保存
// 循环表达式
for _, str := range infix {
// 遇到数字时,将其放入 suffixes
if isNum(str) {
suffixes = append(suffixes, str)
continue
}
if str == "(" {
// 如果是 ( 直接入栈
_ = stack.Push(str)
continue
}
if str == ")" {
for stack.Peek() != "(" {
// 弹出 stack 中栈顶的元素,并追加到 suffixes
elem, _ := stack.Pop()
suffixes = append(suffixes, elem)
}
// 弹出 (,消除一对 ( )
_, _ = stack.Pop()
continue
}
// 如果是运算符
opt, ok := opts[str]
if ok {
if stack.IsEmpty() || stack.Peek() == "(" {
// 如果 stack 为空或栈顶运算符为左括号 "(",则直接将此运算符入栈
_ = stack.Push(str)
continue
}
// 栈不为空,并且当前字符串的优先级小于等于栈顶的元素
for !stack.IsEmpty() && priority(opt.operation, stack.Peek()) <= 0 {
elem, _ := stack.Pop()
// 将栈顶的元素追加到 suffixes
suffixes = append(suffixes, elem)
}
// 直接入栈
_ = stack.Push(str)
} else {
panic("无法识别的字符:" + str)
}
}
for !stack.IsEmpty() {
// 将 stack 中剩余的运算符依次追加到 suffixes
elem, _ := stack.Pop()
suffixes = append(suffixes, elem)
}
// 因为这里用的是数组,它里面元素的顺序就是栈元素出栈后逆序排列的顺序
return suffixes
}测试代码如下:
func main() {
expr := "1+((2+3)*4)-5"
expressions := exprToSlice(expr)
fmt.Printf("将中缀表达式放入切片, 结果为:%v\n", expressions)
expressions = infixToSuffix(expressions)
fmt.Printf("中缀表达式转换成后缀表达式, 结果为:%v\n", expressions)
result := calSuffixExpression(expressions)
fmt.Printf("计算表达式%s, 结果为:%v\n", expr, result)
}输出:
将中缀表达式放入切片, 结果为:[1 + ( ( 2 + 3 ) * 4 ) - 5]
中缀表达式转换成后缀表达式, 结果为:[1 2 3 + 4 * + 5 -]
计算表达式1+((2+3)*4)-5, 结果为:16注意:这里只能计算整数,且表达式前后不能有空格。