数据结构学习总结(五)树
文章目录
- 1. 树的定义及基本术语
- 1.1 定义
- 1.2 基本术语
- 2. 树的抽象数据类型
- 3. 树的存储结构
- 3.1 双亲表示法
- 3.2 孩子表示法
- 3.3 孩子兄弟表示法
- 4. 二叉树
- 4.1 二叉树的定义
- 4.1.1 特殊的二叉树
- 4.2 二叉树的性质
- 4.3 二叉树的存储结构
- 4.3.1 顺序存储结构
- 4.3.2 链式存储结构
- 4.4 遍历二叉树
- 4.4.1 前序遍历
- 4.4.2 中序遍历
- 4.4.3 后序遍历
- 4.4.4 层序遍历
- 5. 线索二叉树
- 6. 树、森林与二叉树的转换
- 6.1 树转换为二叉树
- 6.2 二叉树转换为树
- 6.3 森林转换为二叉树
- 6.4 二叉树转换为森林
- 6.5 树与森林的遍历
- 7. 赫夫曼树
- 7.1 基本概念
- 7.2 Huffman 树的构建
- 7.2 Huffman 编码
1. 树的定义及基本术语
1.1 定义
树是由一个集合以及在该集合上定义的一种关系构成的。我们可以形式地给出树的递归定义如下:
树(Tree) 是 n (n ≥ 0) 个结点的有限集。n = 0 时称为空树。在任意一棵非空树中有:
(1)有且仅有一个特定的称为根(Root)的结点;
(2)当 n>1 时,其余结点可分为 m (m>0) 个互不相交的有限集 T1、T2、……、 Tm,其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。
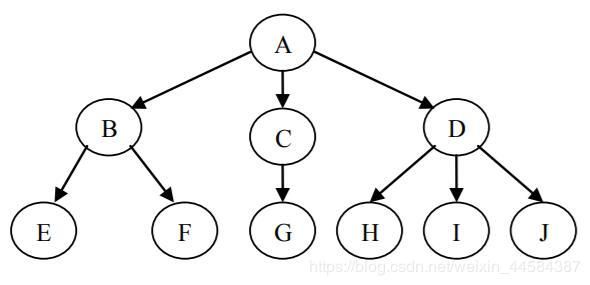
如图是一棵有 10 个结点的树,其中 A 是根,其余的结点分成 3 个互不相交的集合:T1 = {B,E,F}、T2 = {C,G}、T3 = {D,H,I,J},每个集合都构成一棵树,且都是根 A 的子树。例如 T1 是一棵树,其中 B 是根,其余结点构成 2 个互不相交的集合:T11 = {E}、T12 = {F} 是 B 的子树,并且都是只有一个根结点的树。
1.2 基本术语
-
结点的度与树的度
结点拥有的子树的数目称为结点的度(Degree)。度为 0 的结点称为叶结点(Leaf)或终端结点。度不为 0 的结点称为非终端结点或分支结点。除根之外的分支结点也称为内部结点。树的度是树内各结点的度的最大值。例如,在上图中,结点 A、D 的度为 3,结点 E、F、G、H、I、J 的度均为 0,是叶结点。树内各结点的度的最大值是 3,所以树的度是 3。
-
结点间关系
结点的子树的根称为该结点的孩子(Child),相应地,该结点称为孩子的双亲(Parent)。恩,为什么不是父或母,叫双亲呢?对于结点来说其父母同体,唯一的一个,所以只能把它称为双亲了。同一个双亲的孩子之间互称兄弟(Sibling),双亲在同一层次的结点互为堂兄弟。结点的祖先是从根到该结点所经分支上的所有结点。反之,以某结点为根的子树中的任一结点都称为该结点的子孙。例如,在上图中,结点 A 是结点 B、C、D 的双亲,结点 B、C、D 是结点 A 的孩子。由于结点 H、I、J 有同一个父结点 D,因此它们互为兄弟。结点 H 的祖先为结点 A、D。结点 B 的子孙有结点 E、F。结点 E、F 与结点 G、H、I、J 互为堂兄弟。
-
结点的层次和树的深度
结点的层次(Level) 从根开始定义起,根为第一层,根的孩子为第二层。若某结点在第 L 层,则其子树的根就在第 L+1 层。树中结点的最大层次称为树的深度(Depth)或高度。例如,在上图中,结点 A 在第 1 层,结点 B、C、D 在第 2 层,结点 E、F、G、
H、I、J 在第 3 层。显然,当前树的深度为 3。 -
有序树、m 叉树、森林
如果将树中结点的各子树看成从左至右是有次序的,不能互换的,则称该树为有序树,否则称为无序树。若不特别指明,一般讨论的树都是有序树。树中所有结点最大度数为 m 的有序树称为 m 叉树。
森林(Forest) 是 m (m ≥ 0) 棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林。树和森林的概念相近。删去一棵树的根,就得到一个森林;反之,加上一个结点作为树根,森林就变为一棵树。
例如,在上图中,以结点 A 为根的树就是一棵 3 叉树。结点 A 的所有子树就可以组成一个森林。
对比线性表与树的结构,它们有很大的不同,如下表所示。
| 线性结构 | 树结构 |
|---|---|
| 第一个数据元素:无前驱 | 根结点:无双亲,唯一 |
| 最后一个数据元素:无后继 | 叶结点:无孩子,可以多个 |
| 中间元素:一个前驱一个后继 | 中间结点:一个双亲多个孩子 |
2. 树的抽象数据类型
ADT 树(tree)
Data
树是由一个根结点和若干棵子树构成。树中结点具有相同数据类型及层次关系。
Operation
getSize(): 返回树的结点数。
getRoot(): 返回树根结点。
getParent(x): 返回结点 x 的双亲结点。
getDepth(T): 返回树T的深度。
getFirstChild(x): 返回结点 x 的第一个孩子。
getNextSibling(x): 返回结点 x 的下一个兄弟结点,如果 x 是最后一个孩子,则返回空。
...
end ADT
3. 树的存储结构
说到存储结构,就会想到我们前面讲过的顺序存储和链式存储两种结构。
先来看看顺序存储结构,用一段地址连续的存储单元依次存储线性表的数据元素。这对于线性表来说是很自然的,对于树这样一多对的结构呢?
树中某个结点的孩子可以有多个,这就意味着,无论按何种顺序将树中所有结点存储到数组中,结点的存储位置都无法直接反映逻辑关系,你想想看,数据元素挨个的存储,谁是谁的双亲,谁是谁的孩子呢?简单的顺序存储结构是不能满足树的实现要求的。
不过充分利用顺序存储和链式存储结构的特点,完全可以实现对树的存储结构的表示。我们这里要介绍三种不同的表示法:双亲表示法、孩子表示法、孩子兄弟表示法。
3.1 双亲表示法
设 T 是一棵树,表示 T 的一种最简单的方法是用一个一维数组存储每个结点,数组的下标就是结点的位置指针,每个结点中有一个指向各自的双亲结点的数组下标的域。由于树中每个结点的双亲是唯一的,所以上述的双亲表示法可以唯一地表示任何一棵树。
其中 data 是数据域,存储结点的数据信息。而 parent 是指针域,存储该结点的双亲在数组中的下标。由于根结点是没有双亲的,所以我们约定根结点的指针域设置为 -1,这也就意味着,我们所有的结点都存有它双亲的位置。如下图中的树结构和表中的树双亲表示所示。

这样的存储结构,我们可以根据结点的 parent 指针很容易找到它的双亲结点,所用的时间复杂度为 O(1),直到 parent 为 -1 时,表示找到了树结点的根。可如果涉及查询孩子和兄弟信息的树操作,可能要遍历整个数组才行。也可以重新设计存储结构,增加孩子域和兄弟域。
3.2 孩子表示法
树的另一种常用的表示方法就是孩子链表表示法。这种表示法用一个线性表来存储树的所有结点信息,称为结点表。对每个结点建立一个孩子表。孩子表中只存储孩子结点的地址信息,可以是指针,数组下标甚至内存地址。由于每个结点的孩子数目不定,因此孩子表常用单链表来实现,因此这种表示法称为孩子链表表示法。如下图所示。

为此,设计两种结点结构,一个是孩子链表的孩子结点,其中 child 是数据域,用来存储某个结点在表头数组中的下标。next 是指针域,用来存储指向某结点的下一个孩子结点的指针。如下图

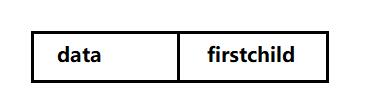
另一个是表头数组的表头结点,其中 data 是数据域,存储某结点的数据信息。firstchild 是头指针域,存储该结点的孩子链表的头指针。如下图
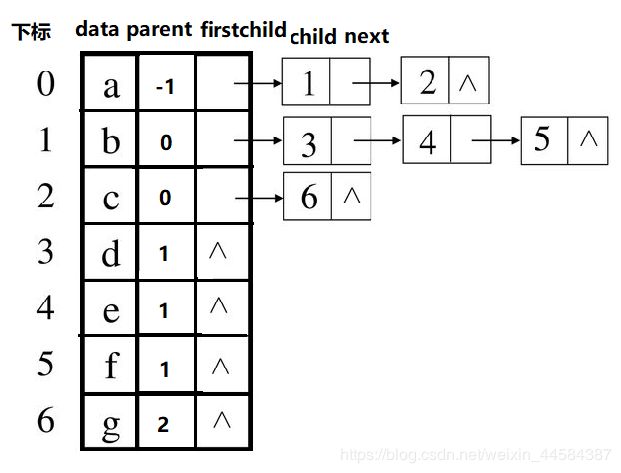
在孩子链表表示法中,通过某个结点找到其孩子较为容易,只需要遍历其孩子链表即可找到其所有孩子结点,然而要找到某个结点的父结点却需要对每个结点的孩子链表进行遍历,比较麻烦。因此可以在孩子链表表示法的基础上结合双亲表示法,在每个结点中再附设一个指示双亲结点的域,这样就可以在 O(1) 时间内找到父结点。如下图
3.3 孩子兄弟表示法
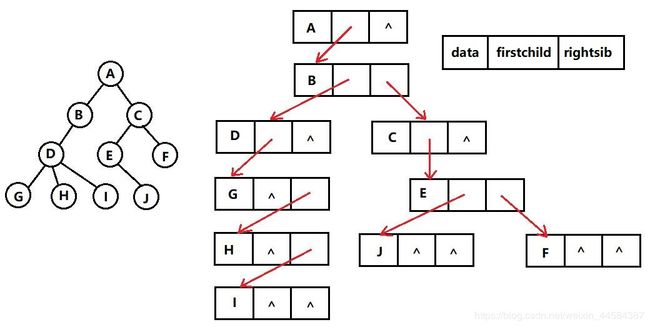
树的孩子兄弟表示法又称为二叉树表示法。每个结点除了 data 域外,还含有两个域,分别指向该结点的第一个孩子(firstchild)和此结点的右兄弟(rightsib)。如图所示。
在图中是使用二叉链表进行存储,这种结构便于实现树的各种操作。如果在二叉链表的每个结点中多增设一个 parent 域,则同样可以方便地实现查找父结点的操作。
4. 二叉树
4.1 二叉树的定义
每个结点的度均不超过 2 的有序树,称为二叉树(binary tree)。与树的递归定义类似,二叉树的递归定义如下:
二叉树是 n(n ≥ 0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者是一棵由一个根结点和两棵互不相交的,分别称为根的左子树和右子树的二叉树组成。
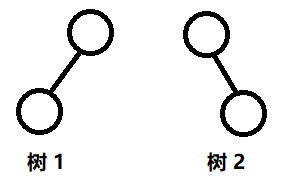
由以上定义可以看出,二叉树中每个结点的孩子数只能是 0、1 或 2 个,并且每个孩子都有左右之分。位于左边的孩子称为左孩子,位于右边的孩子称为右孩子;以左孩子为根的子树称为左子树,以右孩子为根的子树称为右子树,左子树和右子树是有顺序的,次序不能任意颠倒;即使树中某结点只有一颗子树,也要区分它是左子树还是右子树,下图就是两颗不同的二叉树。
4.1.1 特殊的二叉树
斜树
顾名思义,树一定是要斜的,但是往哪斜还是有讲究。所有结点都只有左子树的二叉树叫左斜树,所有结点都只有右子树的二叉树叫右斜树,这两者统称为斜树。如上图,树 1 是左斜树,树 2 是右斜树。
满二叉树
在一颗二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。
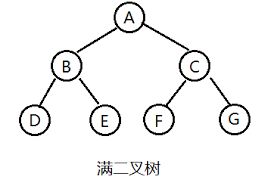
满二叉树的特点:
(1)叶子只能出现在最下一层。
(2)非叶子结点的度一定是 2。
(3)在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多。
完全二叉树
若在一棵满二叉树中,在最下层从最右侧起去掉相邻的若干叶子结点,得到的二叉树即为完全二叉树。
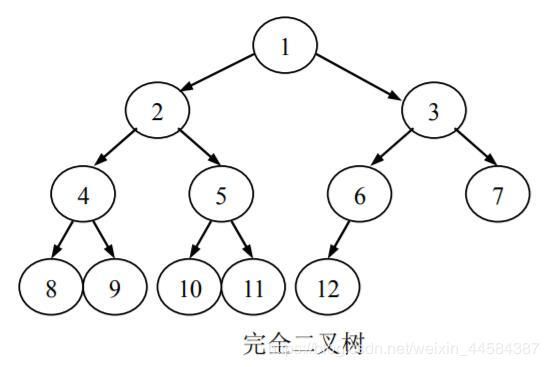
从根结点起,层间自上而下,层内自左而右,逐层由 1 到 n 进行标号,对具有 n 个结点的完全二叉树中结点进行编号,那么完全二叉树中 1~ n 号结点的位置与满二叉树中 1~ n 号结点的位置是一致的。
可见,满二叉树必为完全二叉树,而完全二叉树不一定是满二叉树。
完全二叉树的特点:
(1)叶子结点只能出现在最下两层。
(2)最下层的叶子一定集中在左部连续的位置。
(3)倒数第二层,若有叶子结点,一定都在右部连续位置。
(4)如果结点度为 1,则该结点只有左孩子,即不存在只有右子树的情况。
(5)同样结点的数的二叉树,完全二叉树的深度最小。
4.2 二叉树的性质
性质 1:树中的结点数等于树的边数加 1,也等于所有结点的度数之和加 1。
这是因为两个结点用一条边连接,边数等于所有结点的度数。
性质 2:在二叉树的第 i 层上最多有 2i-1 个结点。
性质 3:深度为 k 的二叉树至多有 2k-1 个结点(k ≥ 1)。
性质 4:对任何一棵二叉树 T,如果其终端结点(叶结点)数为 n0,度为 2 的结点数为 n2,则 n0 = n2 + 1。
证明:假设二叉树中结点总数为 n,度为 1 的结点数为 n1
于是有:n = n0 + n1 + n2
由性质 1 知:n = 1 × n1 + 2 × n2 + 1
所以:n0 = n2 + 1
性质 5:具有 n 个结点的完全二叉树的深度为 ⎣ l o g 2 n ⎦ + 1 ⎣ log_2n ⎦+1 ⎣log2n⎦+1( ⎣ x ⎦ 表示不大于 x 的最大整数)。
证明:假设深度为 k,根据性质 3 以及完全二叉树的定义有
2 k − 1 − 1 < n ≤ 2 k − 1 2^{k-1} -1 < n ≤ 2^k -1 2k−1−1<n≤2k−1,由于 n 是整数,所以
2 k − 1 ≤ n < 2 k 2^{k-1} ≤ n < 2^k 2k−1≤n<2k,两边取对数,得
k − 1 ≤ l o g 2 n < k k - 1 ≤ log_2n<k k−1≤log2n<k,而 k 作为深度也是整数,因此 k = ⎣ l o g 2 n ⎦ + 1 k=⎣ log_2n ⎦+1 k=⎣log2n⎦+1
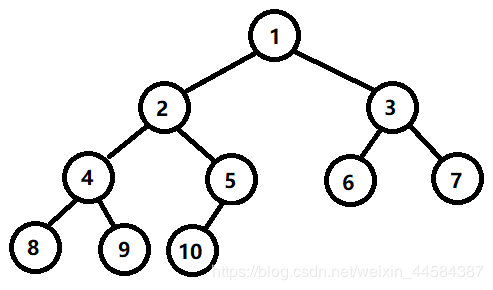
性质 6:如果对一棵有 n 个结点的完全二叉树的结点进行编号,则对任一结点 i (1 ≤ i ≤ n),有:
(1)如果 i = 1,则结点 i 是二叉树的根,无双亲;如果 i>1,则其双亲结点是 ⎣ i/2 ⎦。
(2)如果 2i>n,则结点 i 无左孩子(结点 i 为叶子结点);否则其左孩子是结点 2i。
(3)如果 2i +1>n,则结点 i 无右孩子;否则其右孩子是结点 2i +1。
这里以图为例,来帮助理解这个性质。
4.3 二叉树的存储结构
4.3.1 顺序存储结构
对于满二叉树和完全二叉树来说,可以将其数据元素逐层存放到一组连续的存储单元中,如图所示,用一维数组来实现顺序存储结构时,将二叉树中编号为 i 的结点存放到数组中的第 i 个分量中。如此根据性质 6,可以得到结点 i 的双亲结点、左右孩子结点分别存放在、⎣ i/2 ⎦、2i 以及 2i +1 分量中。
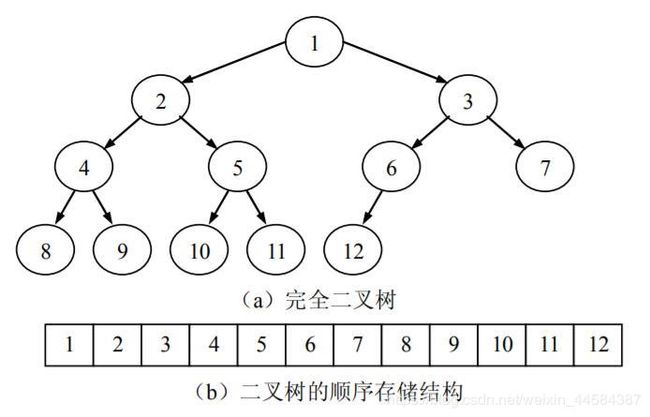
这种存储方式对于满二叉树和完全二叉树是非常合适也是高效方便的。因为满二叉树和完全二叉树采用顺序存储结构既不浪费空间,也可以根据公式很快的确定结点之间的关系。但是对于一般的二叉树而言,必须用“虚结点”将一棵二叉树补成一棵完全二叉树来存储,否则无法确定结点之间的关系,但是这样一来就会造成空间的浪费。一种极端的情况是,为了存储 k个结点,需要 2k-1 个存储单元,如下图所示。此时存储空间浪费巨大,这是顺序存储结构的一个缺点。

4.3.2 链式存储结构
既然顺序存储适用性不强,就考虑用链式存储结构。二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域是比较自然的想法,我们称这样的链表为二叉链表。结点结构如图所示。

其中 data 是数据域,lchild 和 rchild 都是指针域,分别存放指向左孩子和右孩子的指针。
二叉链表如下图。
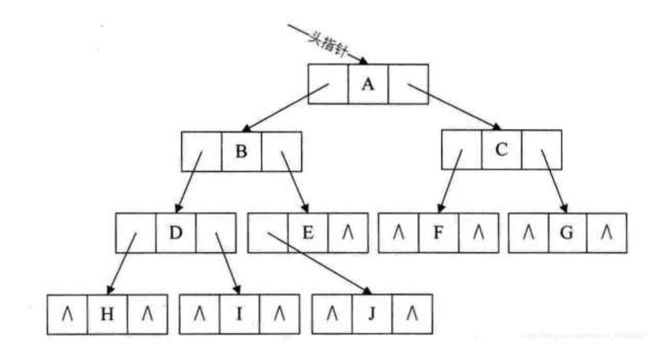
如有需要,还可以在增加一个指向其双亲的指针域,那样就称之为三叉链表了。
4.4 遍历二叉树
二叉树的遍历(traversing binary tree)是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。
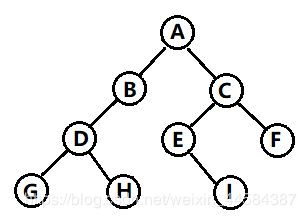
4.4.1 前序遍历
若二叉树为空,则空操作;否则
① 访问根结点;
② 前序遍历左子树;
③ 前序遍历右子树。
上图遍历顺序为:ABDGHCEIF。
4.4.2 中序遍历
若二叉树为空,则空操作;否则从根结点开始(注意并不是先访问根结点)
① 中序遍历左子树;
② 访问根结点;
③ 中序遍历右子树。
上图遍历顺序为:GDHBAEICF。
4.4.3 后序遍历
若二叉树为空,则空操作;否则
① 后序遍历左子树;
② 后序遍历右子树;
③ 访问根结点。
上图遍历顺序为:GHDBIEFCA。
4.4.4 层序遍历
若树为空,则空操作返回,否则从树的第一层,也就是根结点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问。
上图遍历顺序为:ABCDEFGHI。
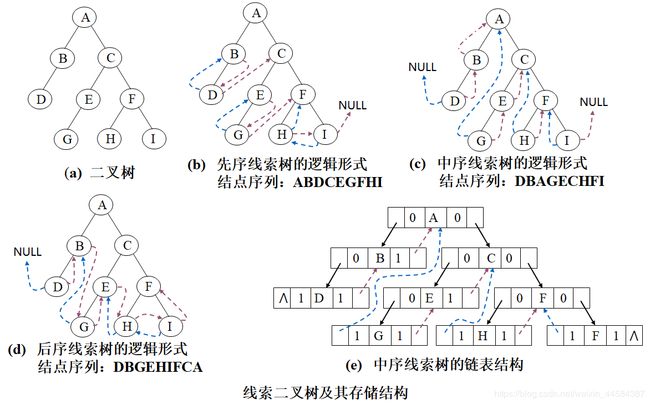
5. 线索二叉树

我们再来观察上图,会发现指针域并不是都充分的利用了,而是有许许多多的 “ ^ ”,也就是空指针域的存在,这实在不是好现象,应该要想办法利用起来。
首先我们要来看着这空指针有多少个呢?对于一个有n个结点的二叉链表,每个结点有指向左右孩子的两个指针域,所以一共是 2n 个指针域。而 n 个结点的二叉树一共有 n-1 条分支线数,也就是说,其实是存在 2n-(n-1)=n+1 个空指针域。比如上图有 10 个结点,而带有 “ ^ ” 空指针域有 11 个。这些空间不存储任何事物,白白的浪费着内存的资源。
另一方面,我们在做遍历时,比如对上图做中序遍历时,得到了 HDIBJEAFCG 这样的字符序列,遍历过后,我们可以知道,结点 I 的前驱是 D,后继是 B,结点 F 的前驱是 A 后继是 C。也就是说,我们可以很清楚的知道任意一个结点,它的前驱和后继是哪一个。
可是这是建立在已经遍历过的基础之上的。在二叉链表上,我们只能知道每个结点指向其左右孩子结点的地址,而不知道某个结点的前驱是谁,后继是谁。要想知道,必须遍历一次。以后每次需要知道时,都必须先遍历一次。为什么不考虑在创建时就记住这些前驱和后继呢,那将是多大的时间上的节省。
综合刚才两个角度的分析后,我们可以考虑利用那些空指针,存放指向结点在某种遍历次序下的前驱和后继结点的地址。
对结点的指针域做如下规定:
◆ 若结点有左孩子,则 Lchild 指向其左孩子,否则,指向其直接前驱;
◆ 若结点有右孩子,则 Rchild 指向其右孩子,否则,指向其直接后继;
为避免混淆,对结点结构加以改进,增加两个标志域,如下图所示。

其中 :
• Ltag 为 0 时指向该结点的左孩子,为 1 时指向该结点的前驱。
• Rtag 为 0 时指向该结点的右孩子,为 1 时指向该结点的后继。
我们把这种指向前驱和后继的指针称为线索,加上线索的二叉链表称为线索链表;按照某种次序遍历,加上线索的二叉树称之为线索二叉树(Threaded Binary Tree)。
说明:画线索二叉树时,实线表示指针,指向其左、右孩子;虚线表示线索,指向其直接前驱或直接后继。
在线索树上进行遍历,只要先找到序列中的第一个结点,然后就可以依次找结点的直接后继结点直到后继为空为止。
如何在线索树中找结点的直接后继? 以图中 (c),(e) 所示的中序线索树为例:
◆ 树中所有叶子结点的右链都是线索。右链直接指示了结点的直接后继,如结点 G 的直接后继是结点 E。
◆ 树中所有非叶子结点的右链都是指针。根据中序遍历的规律,非叶子结点的直接后继是遍历其右子树时访问的第一个结点,即右子树中最左下的(叶子)结点。如结点 C 的直接后继:沿右指针找到右子树的根结点 F,然后沿左链往下直到 Ltag=1 的结点,即为 C 的直接后继结点 H。
如何在线索树中找结点的直接前驱? 若结点的 Ltag=1,则左链是线索,指示其直接前驱;否则,遍历左子树时访问的最后一个结点(即沿左子树中最右往下的结点)为其直接前驱结点。
6. 树、森林与二叉树的转换
在上面提到的树的存储结构,通过孩子兄弟表示法可以将一棵树用二叉链表进行存储,所以借助二叉链表,树和二叉树可以相互进行转换。
◆ 从物理结构来看,树和二叉树的二叉链表是相同的,只是对指针的逻辑解释不同而已。
◆ 从树的二叉链表表示的定义可知,任何一棵和树对应的二叉树,其右子树一定为空。
下图直观地展示了树和二叉树之间的对应关系。
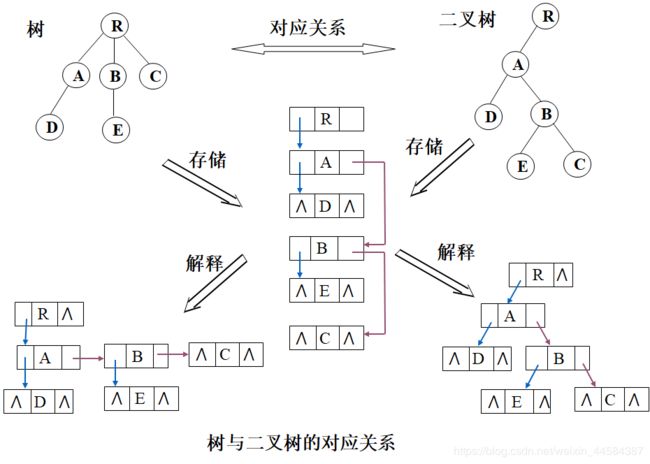
6.1 树转换为二叉树
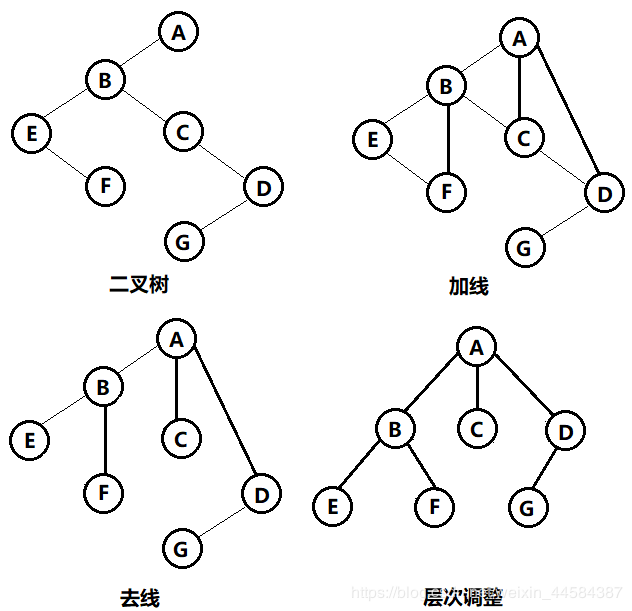
将树转换成二叉树在孩子兄弟表示法中已给出,其详细步骤是:
(1)加线。在所有兄弟结点之间加一条连线。
(2)去线。对树中每个结点,只保留它与第一个孩子结点的连线,删除它与其它孩子结点之间的连线。
(3)层次调整。以树的根结点为轴心,将整棵树顺时针旋转一定的角度,使之结构层次分明。注意第一个孩子是二叉树结点的左孩子,兄弟转换过来的是结点的右孩子。

6.2 二叉树转换为树
二叉树转换为树是树转换为二叉树的逆过程,也就是反过来做而已。步骤如下:
(1)加线。若某结点的左孩子结点存在,则将这个左孩子的右孩子结点、右孩子的右孩子结点、右孩子的右孩子的右孩子结点 ······ 哈,反正就是左孩子的 n 个右孩子结点都作为此结点的孩子。将该结点与这些右孩子结点用线连接起来。
(2)去线。删除原二叉树中所有结点与其右孩子结点的连线。
(3)层次调整。使之结构层次分明。
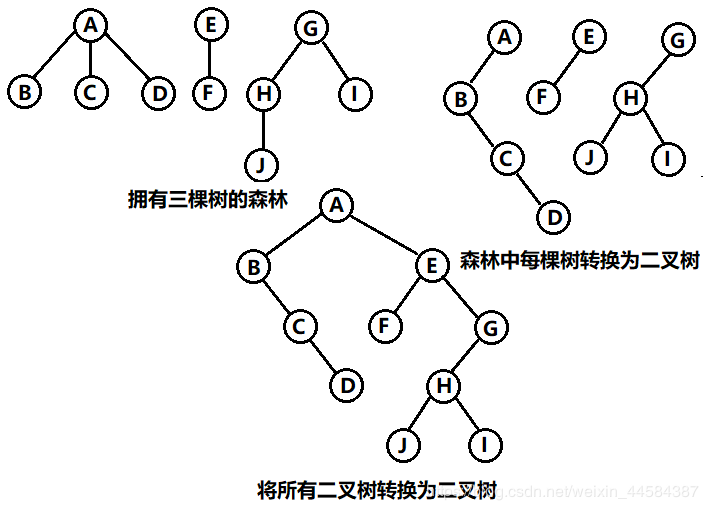
6.3 森林转换为二叉树
森林是由若干棵树组成的,所以完全可以理解为,森林中的每一棵树都是兄弟,可以按照兄弟的处理办法来操作。步骤如下:
(1)把每棵树转换为二叉树。
(2)第一颗二叉树不动,从第二颗开始,依次把后一颗二叉树的根结点作为前一颗二叉树根结点的右孩子,用线连接起来。当所有的二叉树连接起来后就得到了由森林转换来的二叉树。
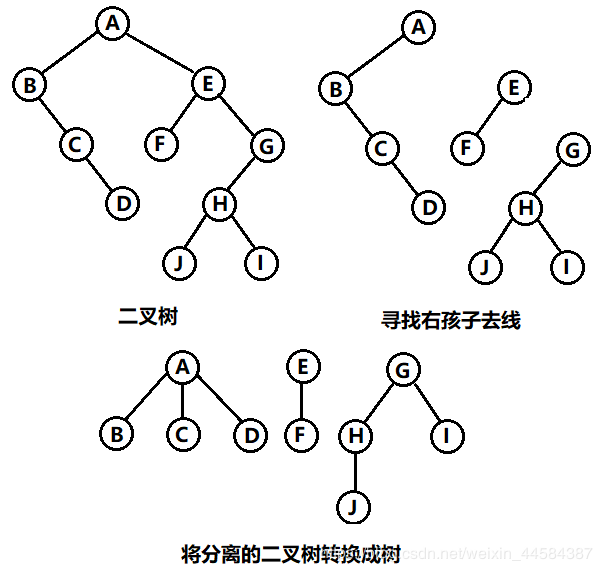
6.4 二叉树转换为森林
判断一颗二叉树能够转换成一棵树还是森林,标准很简单,那就是只要看这棵二叉树的根结点有没有右孩子,有就是森林,没有就是一棵树。那么如果是转换成森林,步骤如下:
(1)先从根结点开始,若有右孩子存在,则把与右孩子结点的连线删除,在查看分离后的二叉树,若有右孩子存在,则连线删除 ······,直到所有右孩子连线都删除为止,得到分离的二叉树。
(2)再将每颗分离后的二叉树转换为树即可。
6.5 树与森林的遍历
树的遍历分为两种方式。
1、一种是先根遍历树,即先访问树的根结点,然后依次先根遍历根的每颗子树。
2、另一种是后根遍历,即先依次后根遍历每颗子树,然后在访问根结点。
比如上图中将二叉树转换成的树,它的先根遍历序列为 ABEFCDG,后根遍历序列为 EFBCGDA。
森林的遍历也分为两种方式:
1、前序遍历:先访问森林中第一棵树的根结点,然后再依次先根遍历根的每颗子树,再依次用同样方式遍历除去第一棵树的剩余树构成的森林。
2、后序遍历:是先访问森林中第一棵树,后根遍历的方式遍历每颗子树,然后再访问根结点,再依次同样方式遍历除去第一棵树的剩余树构成的森林。
比如上边图中将二叉树转换成的森林,前序遍历序列是 ABCDEFGHJI,后序遍历序列是 BCDAFEJHIG。
森林的前序遍历和二叉树的前序遍历结果相同,森林的后序遍历和二叉树的中序遍历结果相同
7. 赫夫曼树
Huffman 树又称最优树,可以用来构造最优编码,用于信息传输、数据压缩等方面,是一类带权路径长度最短的二叉树,有着广泛的应用。
7.1 基本概念
结点路径:从树中一个结点到另一个结点的之间的分支构成这两个结点之间的路径。
路径长度:结点路径上的分支数目称为路径长度。
树的路径长度:从树根到每一个结点的路径长度之和。
结点的带权路径长度:从该结点到树的根结点之间的路径长度与结点上权的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长度之和。记作:
W P L = w 1 ∗ l 1 + w 2 ∗ l 2 + ⋯ + w n ∗ l n = ∑ w i ∗ l i ( i = 1 , 2 , ⋯ , n ) WPL=w_1*l_1+w_2*l_2+⋯+w_n*l_n=\sum w_i*l_i (i=1,2,⋯,n) WPL=w1∗l1+w2∗l2+⋯+wn∗ln=∑wi∗li(i=1,2,⋯,n)
其 中 : n 为 叶 子 结 点 的 个 数 ; w i 为 第 i 个 结 点 的 权 值 ; l i 为 第 i 个 结 点 的 路 径 长 度 。 其中:n 为叶子结点的个数;w_i为第i个结点的权值;l_i为第i个结点的路径长度。 其中:n为叶子结点的个数;wi为第i个结点的权值;li为第i个结点的路径长度。
Huffman 树:它是由 n 个带权叶子结点构成的所有二叉树中带权路径长度 WPL 最小的二叉树,Huffman 树又称最优二叉树。
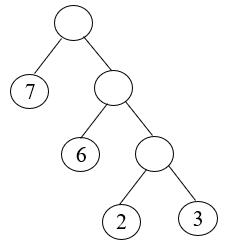
例如上图所示的二叉树,权值为 3 叶子结点,路径长度为 2,该叶结点的带权路径长度为 3∗2=6,树的路径长度为:1+1+2+2+3+3=12,树的带权路径长度3∗2+6∗3+7∗3+2∗1=47。
由以上的定义可知,Huffman 树是带权路径长度最小的二叉树,对于上面的二叉树,其构造完成的 Huffman 树为:
7.2 Huffman 树的构建
由上述的 Huffman 树可知:结点的权越小,其离树的根结点越远。那么应该如何构建Huffman树呢?
① 根据 n 个权值{w1, w2, ⋯,wn},构造成 n 棵二叉树的集合 F={T1,T2,⋯,Tn},其中每棵二叉树只有一个权值为 wi 的根结点,没有左、右子树;
② 在 F 中选取两棵根结点权值最小的树作为左、右子树构造一棵新的二叉树,且新的二叉树根结点权值为其左、右子树根结点的权值之和,注意相对较小的是左孩子,;
③ 在F中删除这两棵树,同时将新得到的树加入 F 中;
④ 重复 ②、③,直到F只含一颗树为止。
构造 Huffman 树时,为了规范,规定 F={T1,T2,⋯,Tn} 中权值小的二叉树作为新构造的二叉树的左子树,权值大的二叉树作为新构造的二叉树的右子树;在取值相等时,深度小的二叉树作为新构造的二叉树的左子树,深度大的二叉树作为新构造的二叉树的右子树。
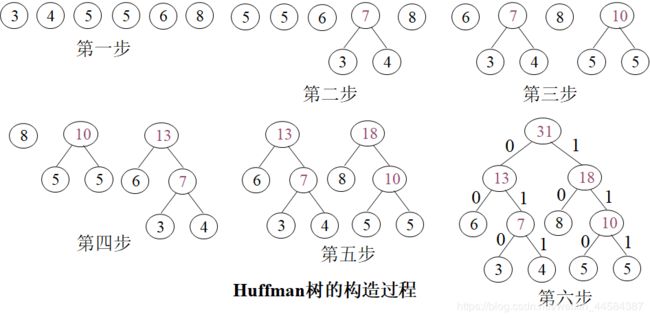
例如,下图是权值集合 W={8,3,4,6,5,5} 构造 Huffman 树的过程。所构造的 Huffman 树的 WPL 是:WPL=6∗2+3∗3+4∗3+8∗2+5∗3+5∗3 =79。
7.2 Huffman 编码
在电报收发等数据通讯中,常需要将传送的文字转换成由二进制字符 0、1 组成的字符串来传输。为了使收发的速度提高,就要求电文编码要尽可能地短。此外,要设计长短不等的编码,还必须保证任意字符的编码都不是另一个字符编码的前缀,这种编码称为前缀编码。
Huffman 树可以用来构造编码长度不等且译码不产生二义性的编码。
设电文中的字符集 C={c1,c2,⋯,ci,⋯,cn},各个字符出现的次数或频度集 W={w1,w2,⋯,wi,⋯,wn}。
Huffman 编码方法:
以字符集 C 作为叶子结点,次数或频度集 W 作为结点的权值来构造 Huffman 树。规定 Huffman 树的左分支代表 0,右分支代表 1,则从根结点到叶子结点所经过的路径分支组成的 0 和 1 序列便为该结点所对应的编码,称之为 Huffman 编码。
由于每个字符都是叶子结点,不可能出现在根结点到其它字符结点的路径上,所以一个字符的 Huffman 编码不可能是另一个字符的 Huffman 编码的前缀。
若字符集 C={a,b,c,d,e,f} 所对应的权值集合为 W={8,3,4,6,5,5},如上图所示,则字符 a,b,c,d,e,f 所对应的 Huffman 编码分别是:10,010,011,00,110,111。