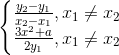椭圆曲线的基础知识
1.名词说明
椭圆曲线离散对数(ESCDP): 离散对数问题是寻找到一个整数指数![]() ,对于整数
,对于整数![]() 和素数
和素数![]() 的一个原根
的一个原根![]() ,使得
,使得![]() 。椭圆曲线上离散曲线是阶
。椭圆曲线上离散曲线是阶![]() 的椭圆曲线,
的椭圆曲线,![]() 点在椭圆曲线上,对于椭圆曲线上的
点在椭圆曲线上,对于椭圆曲线上的![]() 点,寻找
点,寻找![]() ,使得
,使得![]() 。
。
椭圆曲线点乘 : 椭圆曲线![]() 上的点
上的点![]() ,和正整数
,和正整数![]() ,可以得出
,可以得出![]() ,称为椭圆曲线的点乘运算,也能够被称为标量积。
,称为椭圆曲线的点乘运算,也能够被称为标量积。
椭圆曲线的阶:![]() 上椭圆曲线E中的点数
上椭圆曲线E中的点数![]()
椭圆曲线![]() 点的阶:令
点的阶:令![]() 的最小整数。
的最小整数。
Hasse定理:![]() 椭圆曲线上的点数满足
椭圆曲线上的点数满足![]()
2.椭圆曲线
设![]() 是一个域,域
是一个域,域![]() 上的点集满足方程Weierstrass方程:
上的点集满足方程Weierstrass方程:
![]()
其中![]() , 其中
, 其中![]() 为无穷远点。则域K上的椭圆曲线的标准式子为Weierstrass方程。
为无穷远点。则域K上的椭圆曲线的标准式子为Weierstrass方程。
设椭圆曲线E是如下方程:
![]()
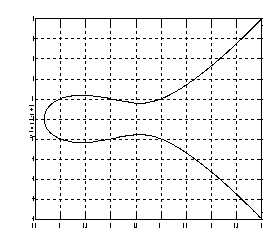
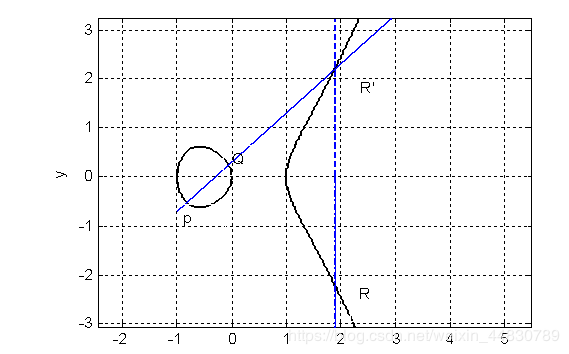
可以知道椭圆曲线E是齐次方程,且满足![]() ,因而椭圆曲线上的每一个点都是光滑的。利用matla,如图2.1,就是椭圆曲线在实数域
,因而椭圆曲线上的每一个点都是光滑的。利用matla,如图2.1,就是椭圆曲线在实数域![]() 上的实例
上的实例
图2.1:椭圆曲线例子
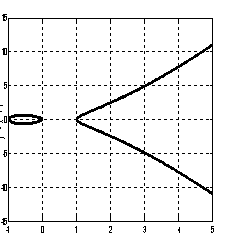
而如图2.2则非实数域上的椭圆曲线,每一个点都是光滑的条件不满足。
图2.2:非椭圆曲线例子
在进行椭圆曲线的研究中,采用如下形式的weierstrass方程,当特征域不为2,3,方程为:![]() .
.
3.椭圆曲线阿贝尔群
定义椭圆曲线为![]() ,椭圆曲线上的运算法则记为
,椭圆曲线上的运算法则记为![]() 。
。
运算法则[2]:椭圆曲线E上的P,Q两点,L是过P,Q两点(如果P=Q,那么L是椭圆曲线上的切线),与椭圆曲线交于R’,过R’做平行于y轴的直线,则与椭圆曲线E相交于点R,![]()
如图2.3椭圆曲线的运算法则示意图如下:
图2.3椭圆曲线运算法则
因此椭圆曲线![]() :
:![]() 上有如下的运算法则
上有如下的运算法则
a. 椭圆曲线![]() 上的直线
上的直线![]() 过
过![]() ,且
,且![]() 为无穷远点,则
为无穷远点,则![]()
b. ![]()
c.![]()
d.设![]() ,存在椭圆曲线
,存在椭圆曲线![]() 上的一点
上的一点![]() ,则
,则![]()
e.![]()
f.![]() ,则
,则
其中:
因而椭圆曲线E上的运算法![]() 则构成了Abel群。
则构成了Abel群。
示例: 有限域![]() 上一条椭圆曲线
上一条椭圆曲线
![]() 上方程:
上方程:![]() ,则
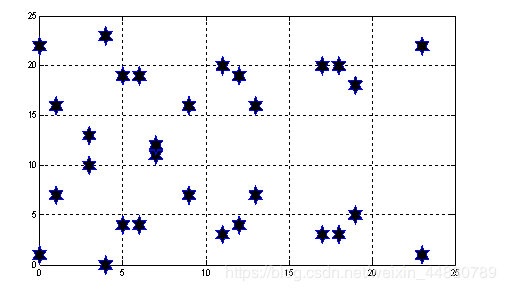
,则![]() 上的点是(0,1),(0,18),(2,7),(2,12),(5,6),(5,13),(7,3),(7,16),(9,6),(9,13),(10,2),(10,17),(13,8),(13,11),(14,2),(14,17),(15,3),(15,16),
上的点是(0,1),(0,18),(2,7),(2,12),(5,6),(5,13),(7,3),(7,16),(9,6),(9,13),(10,2),(10,17),(13,8),(13,11),(14,2),(14,17),(15,3),(15,16),
(16,3),(16,16)
椭圆曲线![]() 的离散点群如图3.1所示
的离散点群如图3.1所示
图3.1:椭圆曲线离散点
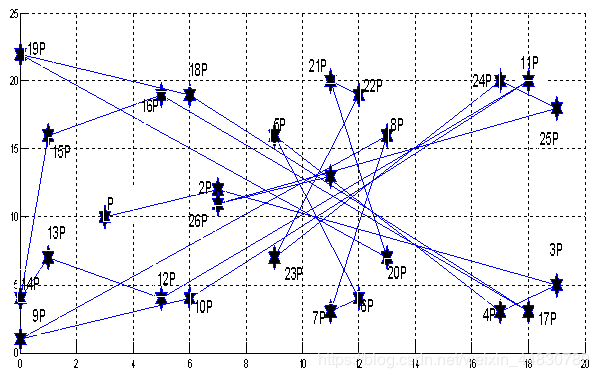
a)取![]()
![]()
![]()
b)取![]()
![]()
![]()
图3.1:标乘p的值