C语言实现椭圆曲线点加
设![]() 是大于3的素数,
是大于3的素数,![]() 上椭圆曲线方程在雅克比坐标下可以简化为
上椭圆曲线方程在雅克比坐标下可以简化为![]() ,其中
,其中![]() ,且
,且![]() 。椭圆曲线的点集可以记做
。椭圆曲线的点集可以记做![]() ,且满足方程。
,且满足方程。
- 若对于

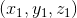 和
和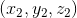 ,若存在某个
,若存在某个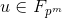 ,使得
,使得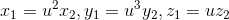 ,则称这三个元素等价
,则称这三个元素等价 - 若
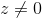 , 记
, 记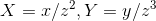 ,则可以从雅克比坐标实现仿射坐标
,则可以从雅克比坐标实现仿射坐标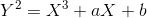
- 若
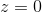 ,
, (1,1,0)代表无穷远点
(1,1,0)代表无穷远点
在雅克比坐标下,![]() 点的运算法则如下:
点的运算法则如下:
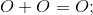
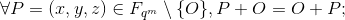
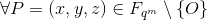 ,逆元素
,逆元素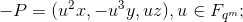
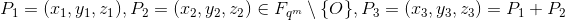
![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
完整的程序代码如下:
#include
#include
#define q 19
int ex_gcd(int a,int b,int &x,int &y)
{
if(b==0)
{
x=1;
y=0;
return a;
}
int r=ex_gcd(b,a%b,x,y);
int t=x;
x=y;
y=t-a/b*y;
return r;
}
/*************************************************************************************************
函数说明:计算z=x mod y
*************************************************************************************************/
void Mod( int x, int y, int &z)
{
z=x%y;
if(z<0)
z=z+y;
}
/*************************************************************************************************
函数说明:雅克比坐标转换为标准投影坐标,其中投影点(X:Y:Z),Z!=0与仿射点(X/Z^2:Y/Z^3)相对应
*************************************************************************************************/
void PNormorlize(int x, int y, int z,
int &x1, int &y1, int &z1)
{
int s,t,m,n;
if (z1!=0)
{
s=z*z;
t=z*s;
ex_gcd(s,q,m,n);
x1=x*m;
ex_gcd(t,q,m,n);
y1=y*m;
Mod(x1,q,x1);
Mod(y1,q,y1);
z1=1;
}
else
{x1=x;y1=y;z1=z;}
}
/*************************************************************************************************
函数说明:在雅克比坐标下,求BNPoint的2倍点(P=Q)
雅克比坐标下的椭圆曲线方程为Y^2=x^3+aXZ^4+bZ^6
如果R=Q+P,P(X1,Y1,Z1),Q(X2,Y2,Z2),R(X3,Y3,Z3),其中P=Q,则有下面的两倍加的计算公式:
见椭圆曲线密码理论的理论与实现p455
这里取椭圆曲线 y^2=x^3+x+1 :
*************************************************************************************************/
void Ptwice(int x1,int y1,int z1,
int &x2,int &y2, int &z2)
{
int a=1;
int t1,t2,t3;
int x,y,z;
if(z1==0) //判断P是否为无穷远点
{x2=x1;y2=y1;z2=z1;} //若是那么相加结果是无穷远点
else //按照上述公式计算
{
t1=3*x1*x1+a*z1*z1*z1*z1;
t2=4*x1*y1*y1;
t3=8*y1*y1*y1*y1;
x2=t1*t1-2*t2;
y2=t1*(t2-x2)-t3;
z2=2*y1*z1;
}
}
/*************************************************************************************************
函数说明:在雅克比坐标下,求BNPoint的2倍点(P!=Q)
雅克比坐标下的椭圆曲线方程为Y^2=x^3+aXZ^4+bZ^6
如果R=Q+P,P(X1,Y1,Z1),Q(X2,Y2,Z2),R(X3,Y3,Z3),则有下面的加法的计算公式:
见椭圆曲线密码理论的理论与实现p455
*************************************************************************************************/
void Padd(int x1, int y1, int z1,
int x2, int y2,int z2,
int &x3, int &y3, int &z3)
{
int t1, t2, t3, t4, t5,t6,t7,t8,t9,t10;
int x,y;
if(z1==0)//判断P是否为无穷远点
{x3=x2;y3=y2;z3=z2;}
else if (z2==0)//判断Q是否为无穷远点
{x3=x1;y3=y1;z3=z1;}
else if ((float)(x1/x2)==(float)(z1/z2)*(z1/z2) &&
(float)(z1/z2)*(z1/z2)*(z1/z2)==(float)(y1/y2) )
Ptwice(x1, y1, z1, x3, y3, z3);
else
{
t1=x1*z2*z2;
t2=x2*z1*z1;
t3=t1-t2;
t4=y1*z2*z2*z2;
t5=y2*z1*z1*z1;
t6=t4-t5;
t7=t1+t2;
t8=t4+t5;
t9=t7*t3*t3;
x3=t6*t6-t9;
t10=t9-2*x3;
y3=(t10*t6-t8*t3*t3*t3);
ex_gcd(2,q,x,y);
y3=y3*x;
z3=z1*z2*t3;
}
}
int main()
{
int a,b,x,y;
int x1=10 ,y1=2,z1=1,x2=9,y2=6,z2=1,x3,y3,z3;
Padd(x1,y1,z1,x2,y2,z2,x3,y3,z3);
printf("椭圆曲线点加: (%d,%d)+(%d,%d)= ",x1,y1,x2,y2);
PNormorlize(x3,y3,z3,x3,y3,z3);
printf("(%d,%d) ",x3,y3);
return 0;
}
实验结果如下图所示:
利用C语言实现大数椭圆曲线加法
/*************************************************************************************************
函数说明:在雅克比坐标下,求BNPoint的2倍点(P!=Q)
雅克比坐标下的椭圆曲线方程为Y^2=x^3+aXZ^4+bZ^6
如果R=Q+P,P(X1,Y1,Z1),Q(X2,Y2,Z2),R(X3,Y3,Z3),则有下面的加法的计算公式:
见椭圆曲线密码理论的理论与实现p455
l1=X1Z1^2
l2=X2Z1^2
l3=t1-t2
l4=Y1Z1^3
l5=Y2Z1^3
l6=l4-l5
l7=l2+l2
l8=l4+l5
Z3=l6^2-l7l3^2
l9=l7l3^2-2t3
Y3=(l9l6-l8l3^3)/2
*************************************************************************************************/
void BN_PAdd(unsigned int x1[], unsigned int y1[], unsigned int z1[],
unsigned int x2[], unsigned int y2[], unsigned int z2[],
unsigned int *x3, unsigned int *y3, unsigned int *z3)
{
unsigned int t1[MAX], t2[MAX], t3[MAX], t4[MAX], t5[MAX];
unsigned int t6[MAX], t7[MAX], t8[MAX], t9[MAX], t[MAX];
unsigned int x[MAX], y[MAX], z[MAX];
unsigned int BN_Two[MAX] = { 1,0x2 };
if (BN_PIsZero(x1, y1, z1))
BN_Passign(x2, y2, z2, x3, y3, z3);
else if (BN_PIsZero(x2, y2, z2))
BN_Passign(x1, y1, z1, x3, y3, z3);
else if (BN_PEqual(x1, y1, z1, x2, y2, z2))
BN_PTwice(x1, y1, z1, x3, y3, z3);
else
{
Mul_Big(z1, z1, t1);
Mod_Big(t1, BN_q, t1);
Mul_Big(z2, z2, t2);
Mod_Big(t2, BN_q, t2);
Mul_Big(z1, t1, t3);
Mod_Big(t3, BN_q, t3);
Mul_Big(z2, t2, t4);
Mod_Big(t4, BN_q, t4);//计算出z1^2,z1^3,z2^2,z2^3
Mul_Big(y2, t3, t3);//计算出z1^3*y2
Mul_Big(y1, t4, t6);//计算出z2^3*y1
Add_Big(t6, t3, t);
Big_SubMod(t6, t3, t6);//计算出
Mul_Big(x2, t1, t3);//计算出z1^2*x2-------->
Mul_Big(x1, t2, t5);//计算出z2^2*x1-------->
Big_SubMod(t5, t3, t7);//计算出t7=t5-t3----->
Mul_Big(z1, z2, t8);
Add_Big(t3, t5, t9);
Mod_Big(t9, BN_q, t9);
Mul_Big(t7, t7, t3);
Mul_Big(t3, t9, t5);
Mod_Big(t5, BN_q, t5);
Mul_Big(t6, t6, x);
Big_SubMod(x, t5, x3);
Mul_Big(t7, t8, z3);
Mod_Big(t5, BN_q, t5);
Mul_Long(x3, 2, x);
Big_SubMod(t5, x, t5);//计算出L10
Mul_Big(t5, t6, t5);
Mod_Big(t5, BN_q, t5);
Mul_Big(t3, t7, t3);
Mod_Big(t3, BN_q, t3);
Mul_Big(t, t3, t);
Mod_Big(t, BN_q, t);
Big_SubMod(t5, t, y);
Inv(BN_Two, BN_q, t);
Mul_Big(t, y, y);
Mod_Big(y, BN_q, y3);
}
}
/*************************************************************************************************
函数说明:在雅克比坐标下,求BNPoint的2倍点(P=Q)
雅克比坐标下的椭圆曲线方程为Y^2=x^3+aXZ^4+bZ^6
如果R=Q+P,P(X1,Y1,Z1),Q(X2,Y2,Z2),R(X3,Y3,Z3),其中P=Q,则有下面的两倍加的计算公式:
见椭圆曲线密码理论的理论与实现p455
t1=3X1^2+aZ1^4
Z3=2Y1Z1
t2=4X1Y1^2
X3=t1^2-2t2
t3=8Y1^4
Y3=t1(t1-X3)-t3
*************************************************************************************************/
void BN_PTwice(unsigned int x1[], unsigned int y1[], unsigned int z1[],
unsigned int *x2, unsigned int *y2, unsigned int *z2)
{
unsigned int t1[MAX], t2[MAX], t3[MAX], t4[MAX], t5[MAX];
unsigned int x[MAX], y[MAX], z[MAX];
if (BN_PIsZero(x1, y1, z1))
BN_Passign(x1, y1, z1, x2, y2, z2);
else
{
Mul_Big(x1, x1, t1);
Mod_Big(t1, BN_q, t1);
Mul_Big(t1, t1, t2);
Mod_Big(t2, BN_q, t2);
Mul_Long(t2, 9, t2);
Mul_Big(y1, y1, t3);
Mul_Big(x1, t3, t4);
Mod_Big(t4, BN_q, t4);
Mul_Long(t4, 8, t5);
Big_SubMod(t2, t5, x);
Mul_Long(t4, 4, t5);
Big_SubMod(t5, x, t5);
Mod_Big(t1, BN_q, t1);
Mul_Big(t1, t5, t5);
Mul_Long(t5, 3, t5);
Mod_Big(t5, BN_q, t5);
Mod_Big(t3, BN_q, t3);
Mul_Big(t3, t3, t4);
Mul_Long(t4, 8, t4);
Big_SubMod(t5, t4, y);
Mul_Big(z1, y1, z);
Add_Big(z, z, z);//计算出z的值
BN_Pconsrtuct(x, y, z, x2, y2, z2);
}
}