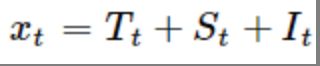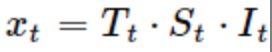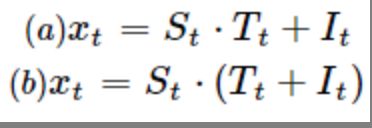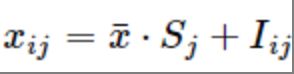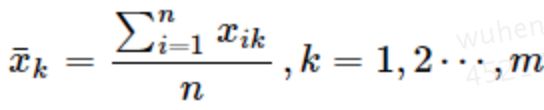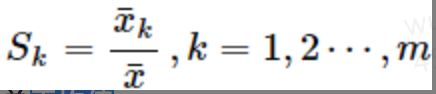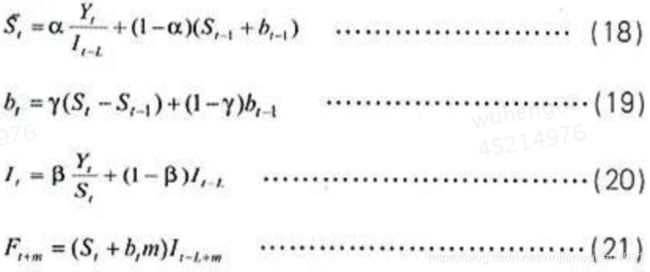时序分析-季节因素
目录
1时序分析的基础
1.1 简介
1.2 分类
2 分析套路
3 主流时序分析模型
3.1移动平均
3.2 指数平滑法
3.3 组合模型
3.4 ARIMA
4 研究细分领域
4.1 异常值检测
4.2 季节序列分析
4.1 同期平均法
4.1.1 简单季节指数法
4.1.2 趋势季节指数法
4.2 长期趋势剔除法
4.2.1 长期趋势剔除法+简单移动平均
4.2.2 温特线性+指数平滑
4.2.3 ARIMA模型+ 时序
4.2.3 季节剔除
5 Java相关包
9 参考资料
1时序分析的基础
1.1 简介
时序分析法的基本思想是事件的发展通常都具有一定的惯性，这种惯性用统计的语言来描述就是序列值之间存在一定的相互关系，而且这种相互关系具有某种统计规律。
事件是随机的，但是规律不是，我们分析的重点就是寻找这种规律，并拟合出适当的数学模型来描述这种规律，进而利用这个拟合模型来预测序列未来的走势。
1.2 分类
平稳的意思简单理解就是整体随机变量整体不会表现出一个趋势。
强平稳 同分布 白噪声 均值和方差都是一个常数，不同时间段的的分布是相同的，也即这些分布的均值和方差是相同的，即是一个常数
弱平稳 随机变量依然没有一个整体的趋势。区别于强平稳的是弱平稳的其随机变量不同时间段的分布是不同的（分布的均值和方差是不同的，但是均值的分布即均值的均值，均值的方差是常数，即均值和方差是稳定的），
变量本身是没有一个趋势的，但是其变量的均值
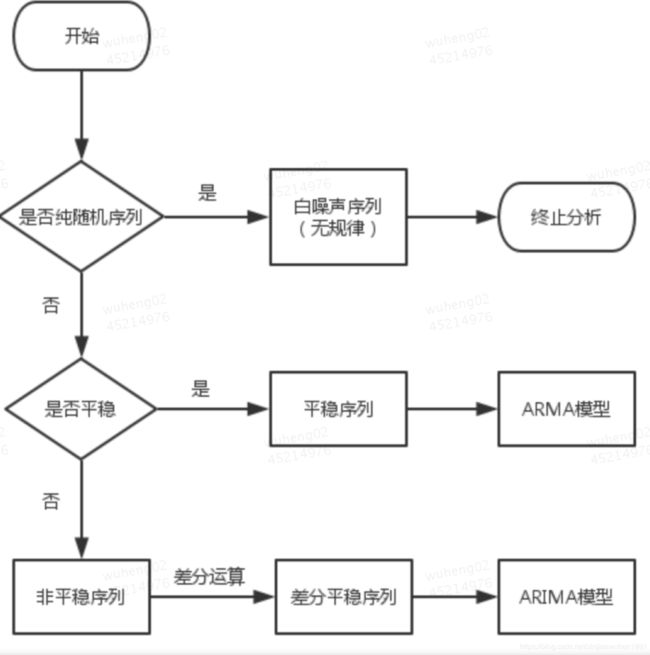
1 长期趋势分析，肯定都是一个不平稳序列，所以必然是用差分的方法转化成平稳序列来分析。
2 目前大部分的研究都是研究弱平稳。
2 分析套路
-
考虑观察值序列的特征
-
根据序列的特征选择适当拟合模型
-
根据序列的观察数据确定模型的口径
-
检验模型，优化模型
-
利用拟合好的模型来推断序列的其他统计性质或预测序列将 来的发展。
3 主流时序分析模型
3.1移动平均
略(股市中有各种移动平均线，可以结合学习感受下)
3.2 指数平滑法
表达式：
1 问：指数平滑的理论基础？
答：从公式可以看出：简单的全期平均法是对时间数列的过去数据一个不漏地全部加以同等利用；移动平均法则不考虑较远期的数据，并在加权移动平均法中给予近期资料更大的权重；而指数平滑法则在不舍弃历史数据的前提下,对离预测期较近的观察值赋予较大的权重，对离预测值较远的观察值赋予较小的权重，达到逐渐减弱对现在预测的影响程度的目的，所以叫做指数平滑法。
2 问：使用场景
应用时间序列平滑法的前提条件是：
A) 所预测的客观事物发展属于渐进式，无跳跃性的变化；
B) 过去和目前影响客观事物发展的因素也决定着客观事物未来的发展
2 问：时间的第一项估计值具体指如何取值？
答：一般分为两种情况，当样本为大样本时（n>42），F1一般以第一期的观察值代替；当样本为小样本时（n<42），F1一般取前几期的平均值代替。
3 问：一次指数平滑优劣势
答：
优势：消除了短期影响，一定程度上能反应变动趋势；相对于普通的移动平均，不会丢弃历史数据。
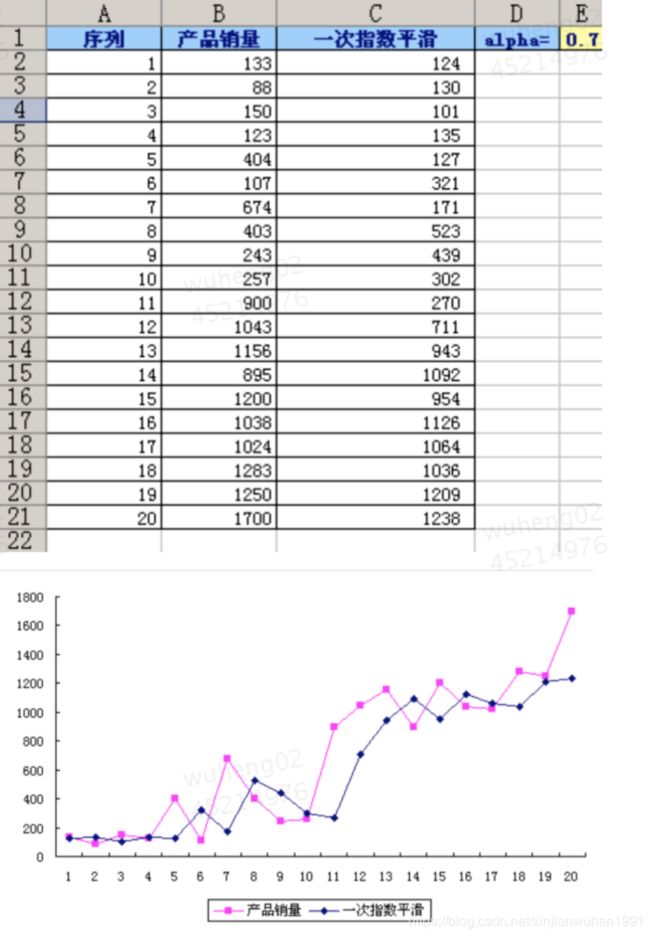
劣势：从下图可以看出，预测趋势与实际变动趋势一致，但预测值比实际值滞后(大多数都是如此，而且移动平均也是也是如此)。
ps:解决办法 --> 多次平滑
CASE：
某产品过去20个月的销售数据如下
从上图可以看出，预测结果和实际值的变化趋势是保持一致的，但是预测结果是滞后于实际值的。
指数平滑模型一般有一次、二次、三次平滑等各种模型。这三种模型分别有不同的特性。
Holt winter和各阶指数平滑之间的关系
Holt winter线性指数平滑法其实就是二次指数平滑法的一种变形
Holt Winter季节性指数平滑法其实就是三次平滑的一种变形
[hotwinter指数平滑模型] https://www.jianshu.com/p/6fb0408b3f54
[时间序列模型] https://my.oschina.net/hosee/blog/1550128
[指数平滑] https://cloud.tencent.com/developer/article/1058557 推荐：本文详细分析了一次、二次、三次、winter线性和季节指数模型的各种使用场景。
三种模型 TODO 预测到底怎么做？
3.3 组合模型
通常时间序列包括3个因素：
-
趋势因素T
-
季节性因素S
-
不规则因素I
常用的综合分析模型有：
加分模型
乘法模型
混合模型
3.4 ARIMA
ARIMA模型 TODO
4 研究细分领域
4.1 异常值检测
refer tangluyang
4.2 季节序列分析
有些时间序列呈现出一定的循环或周期性，这样的时间序列叫季节性时间序列。
时间序列的变动成分可以分成四种，分别是长期趋势、循环变动(周期)、季节变动和不规则变动，分析者可以通过上篇文章的序列图对时间序列进行观察，并结合实际情况判断时间序列中包含的变动成分。
时间序列分解是时间序列分析的传统方法，它的分析思路是将各种变动成分从时间序列中分解出来，并考量引起每种变动成分的原因。时间序列分解有很多优点：
1、分解后的时间序列更加直观简洁，避免各种变动成分之间互相影响；
2、可以分别测定每种变动的影响程度，从而提高预测精度。
季节分析有两种方法：
4.1 同期平均法
4.1.1 简单季节指数法
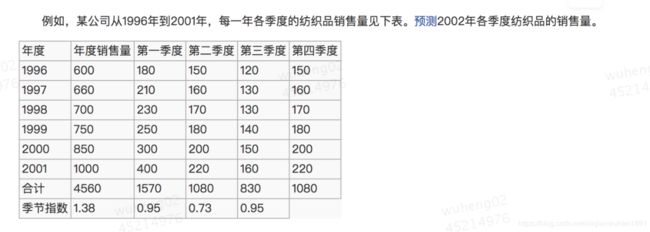
季节性的衡量：所谓季节指数就是用简单平均法计算的周期内各时期季节性影响的相对数。
首先计算周期内各期平均数
然后计算总平均数
再计算季节指数
季节指数反映了该季度与总平均值之间的一种比较稳定的关系：
如果比值大于1，说明该季度的值常常会高于总平均值；
如果比值小于1，说明该季度的值常常低于总平均值；
如果序列的季节指数都近似为1，就说明该序列没有明显的季节性。
从上图可以看出来，第一季度和第三季度有着明显的季节性。可以进行下一步分析，
建立时间序列线性回归预测模型；
结合线性回归预测模型季节指数进行预测
如本例中修正2002年各季度预测值
第一季度预测值=(190+1.90×25)×1.38≈328(单位)
第二季度预测值=(190+1.90×27)×0.95≈229(单位)
第三季度预测值=(190+1.90×29)×0.73≈179(单位)
第三季度预测值=(190+1.90×31)×0.95≈236(单位)
4.1.2 趋势季节指数法
收集并整理历史统计数据（Ai）；
建立预测模型；
利用预测模型求历史上各期的趋势值（Bi）；
求季节指数（Ci）：
Ci = Ai / Bi （实际值/趋势值）
求季节指数的平均值（Fi）；
利用季节指数平均值修正预测值：
yt=（a+bT）Fi相对于简单指数法，此方法区别在于季节指数的求法，是用实际值/趋势值，然后求出一个整体的季节指数平均值。最后修正都用这一个值去修正。
4.2 长期趋势剔除法
4.2.1 长期趋势剔除法+简单移动平均
基本思想就是用基本周期的移动平均，消除季节季节影响。
比如以季度为单位可以，进行四项平均；以月为单位，可以进行12项平均。
接下来，看一个实例https://blog.csdn.net/WMN7Q/article/details/66472665
4.2.2 温特线性+指数平滑
正如上述所述的移动平均的一些问题，所以一般采用含有季节特征的序列分析也会采用指数平滑。
式中，St为时间序列第t期的平滑值，它已剔除季节性因素，bt为时间序列第t期趋势的平滑值，L为季节长度（每年的季数或月数），It为时间序列第t期的季节平滑值，它通常在1附近，一些值大于1，一些值小于1，m为预测的超前期数，Ft+m为时间序列第t+m期的预测值。 使用温特线性和季节性指数平滑法的关键在于一组合理平滑常数组合α、β、γ的选择，从而使预测误差达到最小。需要根据时间序列的特点和预测经验预先确定几对上述常数组合，经过反复测试，计算各组常数组合的预测误差，最后选取预测误差最小的一组得出的结果。
温特线性和季节性指数平滑法也需要选择初始平滑值SL+1和bL+1，一般取：
4.2.3 ARIMA模型+ 时序
ARIMA模型可以对具有季节效应的序列建模，季节ARIMA模型考虑了季节的因素，整体的思路还是先对数据进行平滑预处理，然后交由ARIMA模型进行拟合。
4.2.3 季节剔除
在有些应用中，季节性是次要的，我们需要把它从数据中消除，这个过程叫季节调整，其中季节性差分化是一种常见的方法。
在之前我们介绍过差分（正规差分化），其形式为：
我们将它推广，如果一个序列具有周期性，且周期为s，则季节性差分化为：
5 Java相关包
R和Python有现成的包，比较细致，有细到winter函数的实现。
java的计算包和时间序列相关的比较少。
JMulTi看了下官网没找到非常细致的文档，看他们的Feature，有一些季节模式的假设检验，提供了一些方法；
jmotif 有github，但是没有太多和季节相关的介绍。
网上自定义的java实现的季节ARIMA模型比较多。
9 参考资料
-
[季节时间序列理论与应用] https://baike.baidu.com/item/%E5%AD%A3%E8%8A%82%E6%97%B6%E9%97%B4%E5%BA%8F%E5%88%97%E7%90%86%E8%AE%BA%E4%B8%8E%E5%BA%94%E7%94%A8
-
[浙大时序分析] http://www.cad.zju.edu.cn/home/vagblog/?p=1727
-
[时序分析方法概论和ARIMA模型的历史] https://www.jianshu.com/p/c177dda2d0d5
-
[时序分析基础]http://blog.codinglabs.org/articles/time-series-analysis-foundation.html
-
[完整示例] https://cloud.tencent.com/developer/article/1043845
-
[一次指数平滑法] https://blog.csdn.net/Mary19920410/article/details/77267493
-
[时间序列平滑法如何预测产品产量] https://cloud.tencent.com/developer/article/1058557 ps:包括各种高阶指数平滑，季节处理方法，强烈推荐阅读。
-
[简单季节指数法] https://wiki.mbalib.com/wiki/%E7%AE%80%E5%8D%95%E5%AD%A3%E8%8A%82%E6%8C%87%E6%95%B0%E6%B3%95
-
https://blog.csdn.net/WMN7Q/article/details/66472665
-
[arira + 时序]https://blog.csdn.net/dingming001/article/details/73743950