数据结构课程设计（二）---算术表达式求值

1、任务简述：
一个算术表达式是由操作数(operand)、运算符(operator)和括号组成的。假设操作数均是正实数，运算符只含加减乘除四种运算符。编程利用“算符优先法”求算术表达式的值。

要求：
（1） 从键盘或文件读入一个合法的算术表达式，输出相应的后缀表达式。后缀表达式中，数据与数据之间加分隔符；
（2） 输出正确的计算结果，保留两位小数点；
（3） 考虑算法的健壮性，当表达式错误时，要给出错误提示
（4） 可以连续输入，即输入完一个表达式，转换和计算完成后可以提示用户继续输入表达式，直到用户输入一个“#”则退出程序。

2、算法描述：
数据结构
typedef struct my_stack
{
int a[N];
int top;
}ST;//栈，用来中缀转后缀

在中缀转后缀的代码直接参考了老师的代码，对数字，+,-,*,/分别进行了考虑和判断错误，并且写出了错误原因，在进行求和使，由于有小数点的问题（放在总结里面讨论了），因为我是用char来存放数字，所以转换回去要采用强制转换，例如：(int)a，除此以外没什么问题，一开始，我还在考虑-可以是单目运算符，也可以是多目运算符，但是题目只要求正数，所以只考虑-为双目运算符。
中缀转后缀的具体转换方式:
1.从左到右进行遍历
2.运算数,直接输出.
3.左括号,直接压入堆栈,(括号是最高优先级,无需比较)(入栈后优先级降到最低,确保其他符号正常入栈)
4.右括号,(意味着括号已结束)不断弹出栈顶运算符并输出直到遇到左括号(弹出但不输出)
5.运算符,将该运算符与栈顶运算符进行比较,
如果优先级高于栈顶运算符则压入堆栈(该部分运算还不能进行),
如果优先级低于等于栈顶运算符则将栈顶运算符弹出并输出,然后比较新的栈顶运算符.
(低于弹出意味着前面部分可以运算,先输出的一定是高优先级运算符,等于弹出是因为同等优先级,从左到右运算)
直到优先级大于栈顶运算符或者栈空,再将该运算符入栈.
6.如果对象处理完毕,则按顺序弹出并输出栈中所有运算符.

3、源代码

#include 
#include 
#include 
#include 
#define N 30

//数据结构 
typedef struct my_stack
{
	int a[N];
	int top;
}ST;//栈，用来中缀转后缀 

//所使用的函数 
int isempty(ST *T); //判断栈是否为空 
int isfull(ST *T);  //判断栈是否为满 
int gettop(ST *T);  //得到栈顶元素
int pop(ST *T);  //弹栈 
void push(ST *T,int s);  //入栈 
void transfer(char *in,char *post);   //中缀转后缀 
float Calculate_zhong(char *post);    //计算中缀的值（实际上用后缀来计算） 

//主函数 
main()
{
	char zhong[N],hou[N];     //zhong为中缀表达式 hou为后缀表达式 
	float answer;             //存储计算结果
	system("color 1E");
	printf("--------------081810221朱林昊--------------\n");
	printf("\n--------------表达式求值--------------\n\n");  //说明该代码的实现功能 
	printf("需要计算的中缀表达式为:  ");
	scanf("%s",zhong);
	while(strcmp(zhong,"#")!=0)   //当输入为"#"结束 
	{
		transfer(zhong,hou);     //中缀转后缀 
		printf("\n\n转化后的后缀表达式为：");    //下面的空格，"\n"，"-"只是为了输出好看 
		printf("%s\n",hou);
		printf("\n--------------计算结果--------------\n");
		answer=Calculate_zhong(hou);
		printf("\n           %s",hou);
		printf(" = %f\n",answer);
		printf("\n--------------计算完毕--------------\n");
		printf("\n\n需要计算的中缀表达式为:  ");
	    scanf("%s",zhong);
	}
}

int isempty(ST *T)  //判断栈是否为空 
{
	if(T->top<0)
		return 1;
	else
		return 0;
}

int isfull(ST *T)   //判断栈是否为满 
{
	if(T->top==N-1)
		return 1;
	else
		return 0;
}

int gettop(ST *T)   //得到栈顶元素 
{
	return T->a[T->top];
}

int pop(ST *T)  //弹栈 
{
	int x;
	if(T->top<0)   //栈为空 
	{
		printf("Zhan is empty,can not pop!\n");
		exit(0);
	}
	else
	{
		x=T->a[T->top];
		(T->top)--;
		return x;
	}
}

void push(ST *T,int s)   //入栈 
{
	if(T->top==N-1)  //栈满了 
	{
		printf("Zhan is full,can not push,you can modify N and then you can push again.\n");
		exit(0);
	}
	else
	{
		(T->top)++;
		T->a[T->top]=s;
	}
}

void transfer(char *in,char *post)    //将中缀表达式转化为后缀表达式,参考了老师的代码，加上了关于小数的讨论 
{
	ST T;//栈 
	int i,j,flag=0;    //flag=1说明是现在栈顶是数，用来判断是否出现连续两个运算符
	int count;     //记录每个数中小数点的个数，超过一个则表达式有误	
	int right=0,left=0;     //left和right用来记录算式里面左右括号的个数 
	T.top=-1;
	for(i=0,j=0;in[i]!='\0';i++)
	{
		switch(in[i])
		{
		case '0':
		case '1':
		case '2':
		case '3':
		case '4':
		case '5':
		case '6':
		case '7':
		case '8':
		case '9':for(count=0;(in[i]<='9'&&in[i]>='0')||in[i]=='.';i++,j++)
				{
				 	post[j]=in[i];
				 	if(in[i]=='.') //记录小数点出现的个数 
				 		count++;
				}  
				i--;
				if(count>1)
				{
				 	printf("\n表达式错误!!!!\n\n错误原因：数中有两个小数点\n");
				 	exit(0);
				}
				post[j]=' ';//用空格来分割两个数 
				j++;
				flag=1;  //目前为数字，则flag为1 
				break;
		case '(':if(flag)//如果括号前是数字，则表达式有误 
				{
				 	printf("\n表达式错误!!!!\n\n错误原因：数字后直接跟括号\n");
				 	exit(0);
				}
				push(&T,in[i]); 
				left++;//左括号个数加一 
			    break;
		case ')':right++;   //右括号个数加一 
				while(gettop(&T)!='(')
				{
					 post[j]=pop(&T);
					 j++;
				}
			     pop(&T); 
				 break;
		case '+':
		case '-':if(!flag&&i!=0)//如果运算符前是运算符，则表达式有误
				{
				 	printf("\n表达式错误!!!!\n\n错误原因：有连续两个运算符之间没有数字\n");
				 	exit(0);
				}
				while(!isempty(&T)&&gettop(&T)!='(')
				{
					post[j]=pop(&T);
					j++;
				}
			    push(&T,in[i]);
			    flag=0;//目前为符号，所以flag为0 
				break;
		case '*':
		case '/':if(!flag)//如果运算符前是运算符，则表达式有误 
				{
				 	printf("\n表达式错误!!!!\n\n错误原因：有连续两个运算符之间没有数字\n");
				 	exit(0);
				} 
				while(!isempty(&T)&&(gettop(&T)=='/'||gettop(&T)=='*'))
				{
					 post[j]=pop(&T);
					 j++;
				}
			    push(&T,in[i]);
			    flag=0;
				break;
		default:printf("\n表达式错误!!!!\n\n错误原因：输入非法字符，无法试别\n");
			    exit(0);
		}
	}
	if(left!=right)
	{
		printf("\n表达式错误!!!!\n\n错误原因：左右括号不匹配\n");
		exit(0);
	}
	while(!isempty(&T)) 
	{
		post[j]=pop(&T);
		j++;
	}
	post[j]='\0';
}

float Calculate_zhong(char *post)
{
	int i,j,top=-1,flag;       //top为栈顶，初始值为-1，flag用来判断数字是否存在小数点 
	int len;                   //len表示数字小数点前的长度
	float temp,aa[N];          //aa[N]用来存放表达式中的数字，temp为临时变量 
	char ch[N];                //先把数字的表达式存到ch[N]中，再转化为数字存到aa[N] 
	for(i=0,j;post[i]!='\0';i++)  //依此开始读取栈的后缀表达式的内容 
	{
		if(post[i]>='0'&&post[i]<='9')//如果当前为数字，先将数字存到ch中，再转化为float类型并存到aa中 
		{
			flag=0; //初始为0 
			j=0;  //用来记录字符串的长度 
			while(post[i]!=' ')//将这一串代表数字的字符串存到ch中，直到数字结束 
			{
				if(post[i]=='.')//判断是否有小数点，分别讨论 
					flag=1; //有小数点 
				ch[j]=post[i];//把数字存入到ch[N]中 
				i++;
				j++;
			}
			ch[j]='\0'; //加上这个，表示字符串结尾 
			if(flag)//有小数点的情况，先算小数点前的，再算小数点后的，分开计算 
			{
				for(j=0;ch[j]!='.';j++);//先求长度，找到j的位置，那么长度为j-1 
					len=j-1;
				for(j=0,temp=0.;ch[j]!='.';j++)  //计算小数点前的和
					temp+=(ch[j]-'0')*pow(10,len-j);
				for(j++,len++;ch[j]!='\0';j++)   //计算小数点前的和
					temp+=(ch[j]-'0')*pow(10,len-j);
			}
			else//没小数点的情况
			{
				for(j=0;ch[j]!='\0';j++);//求出相应的长度 
					len=j-1;
				for(j=0,temp=0.;ch[j]!='\0';j++)
					temp+=(ch[j]-'0')*pow(10,len-j);
			}
			top++;
			aa[top]=temp;//temp入栈，到这里对数字的处理就结束了 
		}
		else      //如果是运算符，栈顶两个数出栈，并把这两个数的运算结果入栈！！！！！ 
		{
			switch(post[i])  //根据不同的运算结果进行运算 
			{
				case'+':temp=aa[top];
						top--;
						temp+=aa[top];  //本来这里需要再top--，但是后面由于需要入栈，及需要top++，所以这里就没有做top-- 
						aa[top]=temp;
						break;
				case'-':temp=aa[top];
						top--;
						temp=aa[top]-temp;  //本来这里需要再top--，但是后面由于需要入栈，及需要top++，所以这里就没有做top--
						aa[top]=temp;
						break;
				case'*':temp=aa[top];
						top--;
						temp=temp*aa[top]; //本来这里需要再top--，但是后面由于需要入栈，及需要top++，所以这里就没有做top--
						aa[top]=temp;
						break;
				case'/':temp=aa[top];
						top--;
						temp=aa[top]/temp;   //本来这里需要再top--，但是后面由于需要入栈，及需要top++，所以这里就没有做top--
						aa[top]=temp;
			}
		}
	}
	return aa[top];//最终的计算结果就在栈顶 
}//263行 

4、运行结果
正确情况：

错误情况：



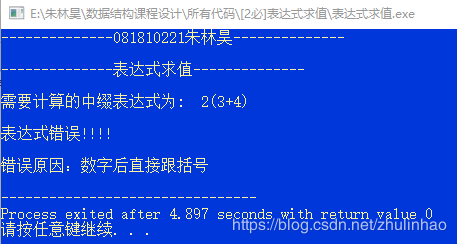
5、总结
性能分析：
时间复杂度：假设表达式有n个数字，m个符号（运算符，括号），那么中缀表达式转后缀表达式操作需要进行n+m次操作，而计算则需要f(m)次(和m有关，计算次数为运算符的个数，即m减去括号的个数，但是可以确定，和m是线性关系，f(m)=km+b)，所以时间复杂度可以认为是O(n+km).
空间复杂度：由于需要用到栈来存放数字和符号，并且在数字，符号之间要加入空格来方便读取操作，所以空间复杂度为O(2n+2m-1)
遇到的问题与解决方法：
小数点问题：即这里要求数字为float或者double类型，那么就会出现小数点，所以我们不妨用char类型来存，然后强制转换，但是对于小数本身，我们也可以分段考虑，考虑小数点前，和小数点后，即把数字拆开来看。
心得体会：
运行结果经过演算，都是正确的，对于错误的表达式，可以说明相应的错误原因。其实这道题可以改进，就是可以不仅仅局限于复数的处理，如果-为单目运算符，那么它可以出现在表达式开头或者右括号的右边，那么我们可以1.特判，直接判断就行了；2.补0；这两个方法都是可以的，但是补0虽然简单，但是其实他改变了表达式（虽然值没有变）。
针对上面的思路，我们可以处理更多的单目运算符，比如”^”,”根号”等等，这个是非常有意义的，比如可以用来自动生成那些小学生计算题的答案，那么网上考试会变得非常方便（即，甚至不用传答案上去，只需要传试卷）
存在问题和改进方法：
这道题由于老师写好了中缀转后缀的代码，所以我也中规中矩的用了栈来写，但是其实可以用二叉树来操作，就像第一题的结构那样，叶子为数字，其父节点先是运算符，然后是计算结果，这样可能在处理功能上更优，比如不需要加空格，那么树来存储比我用栈来存储会节省空间（虽然空间复杂度量级相同，和m+n有关）