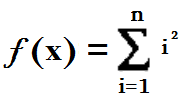【C++习题笔记】谭浩强C++程序设计(第三版)第四章
1. 写两个函数,分别求两个整数的最大公约数和最小公倍数,用主函数调用这两个函数,并输出结果
//两个函数求最大公约数和最小公倍数
#include
using namespace std;
int main()
{
int a,b,c,d;
int maxcm(int a, int b);
int mincd(int a, int b);
cin >> a >> b;
c = maxcm(a,b);
cout << "最大公约数为:"<< c <<'\n';
d = mincd(a,b);
cout <<"最小公倍数为:"<< d <<'\n';
}
int maxcm(int a, int b)
{
int m,n,k;
m = a;
n = b;
do{
k = m % n;
m = n;
n = k;
}while(k);
return m;
}
int mincd(int a, int b)
{
int c,d;
c = maxcm(a,b);
d = a*b/c;
return d;
} 此题注意:函数首部的形参不用在函数中再定义一次;调用函数时,实参前边不用写类型。
此题仍用的是辗转相除法计算的最大公约数与最小公倍数,详细解释请见:https://blog.csdn.net/zl3090/article/details/84614046
2. 求方程ax2+bx+c=0的根.用三个函数分别求当:b2-4ac大于0、等于0和小于0时的根并输出结果。在主程序中输入a,b,c的值。
//三个函数求二次方程的根
#include
#include
using namespace std;
float r1,r2;//全局变量,实根
float p, q;//虚根
int main()
{
float a,b,c;
float t;
void root1(float a, float b, float c);//大于0
void root2(float a, float b, float c);//等于0
void root3(float a, float b, float c);//小于0
cin >> a >> b >> c;
//判别式计算
t = b*b - 4*a*c;
//分情况
if (t>0)
{
root1(a,b,c);
cout << "r1 = " << r1 << '\t'<< "r2 = " << r2 <<'\n';
}
else if (t == 0)
{
root2(a,b,c);
cout << "r1 = " << r1 << '\t'<< "r2 = " << r2 <<'\n';
}
else
{
root3(a,b,c);
cout<<"r1="<< p <<'+'<< q <<'i'<<'\n';
cout<<"r2="<< p <<'-'<< q <<'i'<<'\n';
}
}
void root1(float a, float b, float c)
{
r1 = (-b+sqrt( b*b - 4*a*c))/(2*a);
r2 = (-b-sqrt( b*b - 4*a*c))/(2*a);
}
void root2(float a, float b, float c)
{
r1 = r2 = (-b)/(2*a);
}
void root3(float a, float b, float c)
{
p = -b/(2*a);;
q = sqrt(-(b*b - 4*a*c))/(2*a);
} 此题注意的是,在一个函数中如果想实现多个输出,最简单的方法就是全局变量和void函数的结合
还有其他方法可见:https://blog.csdn.net/qq_34489443/article/details/81274951
3. C++程序 写一个判断素数的函数,在主函数输入一个整数,输出是否为素数的信息。
//素数的判别函数
#include
using namespace std;
int main()
{
int a,r;
r = 0;
int prime(int a);
cin >> a;
r = prime(a);
if (r == 1)
cout << a <<"是素数";
else
cout << a <<"不是素数";
}
int prime(int a)
{
int i,r;
r = 1;
for (i=2;i 此题注意:素数即质数,优化在于for循环中放的是2到a/2之间的数字,只考虑一半即可,因为另一半是和前一半配对的。
4. 求a!+b!+c!的值,用一个函数fac(n)求n!。a,b,c的值由主函数键入,最终的值在主函数中输出。
//递归求阶乘
#include
using namespace std;
int main()
{
int a,b,c,s;
int fac(int a);
cin >> a >> b >> c;
s = fac(a) + fac(b) +fac(c);
cout << a << ','<< b << ','<< c<<"的阶乘之和为"<< s <<'\n';
}
int fac(int a)
{
long r;
r = 0;
if (a <0)
cout <<"error";
else if (a == 1 || a == 0)
r = 1;
else
{
r = a * fac(a-1);
}
return r;
} 此题注意,输出的阶乘为long型,不然太容易溢出。
5. 写一函数求sinh(x)的值,求sinh(x)的近似公式为 sinh(x)=(ex-e(-x))/2其中用一个函数求ex (x在指数位置)
//ex函数的复合函数
#include
#include
using namespace std;
int main()
{
double x,sh;
double ex(double x);
cin >> x;
sh = (ex(x) - ex(-x))/2;
cout << "sinh(x)的值为:"<< sh <<'\n';
}
double ex(double x)
{
double e;
e = exp(x);
return e;
} 6. 用牛顿迭代法求根。方程为ax3+bx2+cx+d=0 系数a,b,c,d的值依次为1,2,3,4, 由主函数输入。求x在1附近的一个实根。求出根后由主函数输出。
牛顿迭代法公式详见:https://baike.baidu.com/item/%E7%89%9B%E9%A1%BF%E8%BF%AD%E4%BB%A3%E6%B3%95/10887580?fr=aladdin
//牛顿迭代法求根
#include
#include
using namespace std;
int main()
{
double a,b,c,d,r;
double newton(double a, double b, double c, double d);
cin >> a >> b >> c >>d;
r = newton(a,b,c,d);
cout << "牛顿迭代法所得的根为:"<< r;
}
double newton(double a, double b, double c,double d)
{
double x= 1,x0,f,f1;
do {
x0 = x;
f=((a*x0+b)*x0+c)*x0+d;
f1=(3*a*x0+2*b)*x0+c;//一阶导
x=x0-f/f1;
}while(fabs(x-x0)>=1e-5);
return x;
} do-while的用法还要加强
7. 写一个函数验证哥德巴赫猜想:一个不小于6的偶数可以表示为两个素数之和,如6=3+3,8=3+5,10=3+7……在主函数输入一个不小于6的偶数N。然后调用函数gotbaha,在gotbaha函数中再调用prime函数,prime函数的作用是判别一个数是否为素数。在godbah函数中输出以下形式的结果:34=3+31
//哥德巴赫猜想
#include
using namespace std;
int main()
{
int e,flag = 0;
int gotbaha(int e);
cin >> e;
flag = gotbaha(e);
if (flag == 1)
cout << "gotbaha is true.";
}
int gotbaha(int e)
{
int a,b,flag = 0;
int prime(int a);
if (e <=5 || e % 2 !=0 )
cout << "Please enter odd number";
else
{
for(a=3;a<=e/2;a=a+2)
{
if(prime(a))
{
b=e-a;
if (prime(b))
flag = 1;
}
}
}
return flag;
}
int prime(int a)
{
int i,r;
r = 1;
for (i=2;i 此题的关键在于如何把一个偶数拆成两个奇数的和,然后分别验证这两个奇数是不是素数。
8. 用递归方法求n阶勒让德多项式的值,递归公式为:
//递归求值
#include
using namespace std;
int main()
{
float n,x,r;
float p(float n,float x);
cin >> n >> x;
r = p(n,x);
cout << "公式的值为"<< r ;
}
float p(float n, float x)
{
if (n==0)
return(1);
else if (n==1)
return(x);
else
return(((2*n-1)*x*p((n-1),x)-(n-1)*p((n-2),x))/n);
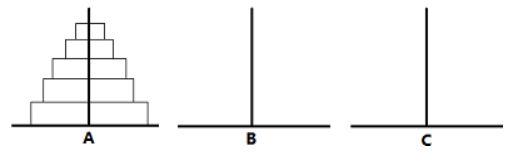
} 9. Hanoi(汉诺)塔问题。这是一个经典的数学问题:古代有一个梵塔,塔内有3个座A,B,C,开始时A座上有64个盘子,盘子大小不等,在的在下,小的在上(见下图)。
有一个老和尚想把这64个盘子从A盘移到C座,但每次只允许移动一个盘,且在移动过程中有3个座上都始终保持在大盘在下,小盘在上。在移动过程中可以利用B座,要求编写程序打印出移动的步骤。
解题思路:采用递归方法,关键在于可以逆向思考,即不考虑前边n-1个盘子是怎么移动的,直接考虑最后一次移动的情况,由题意知,A为原始塔,B为辅助塔,C为目标塔,分为以下三步:
(1)先把A上的n-1个盘子移动到B上(不考虑具体过程,交给递归);
(2)然后把A中最后一个盘子移动到C上;
(3)此时B成为原塔,A为辅助塔,将B中n-2个盘子放到A上(仍不考虑具体过程,交给递归);
此时,一轮移动已结束,下一次的开始,将B中的一个剩下的一个放在C上
理解过程如下动画所示:(参考自:https://www.cnblogs.com/wuzhenbo/p/3496054.html)
三个圆盘的汉诺塔
四个圆盘的汉塔:
代码如下:
//汉诺塔
#include
using namespace std;
int main()
{
int n;
char x, y ,z;
void Hanoi(int n, char x, char y, char z);//原塔,辅助塔,目标塔
cin >> n;
Hanoi(n,'A','B','C');
}
void Hanoi(int n, char x, char y, char z)
{
if (n == 1) cout<<"From "<< x <<" To "< 10. 用递归法将一个整数n转换成字符串。例如 输入483,应输出字符串“483”。n的倍数不确定,可以是任意倍数的整数。
//递归将数字转为字符串
#include
using namespace std;
int main()
{
int n;
void convert(int n);
cin >> n;
if (n<0)
{
cout << "-";
n = -n;
}
convert(n);
}
void convert(int n)
{
int i;
char c;
if ((i =n/10) != 0)
convert(i);
c = n % 10 + '0';
cout<<" "< 单个数字变字符串,给它+‘0’即可
//递归求函数值
#include
using namespace std;
int main()
{
int n,s;
int fac (int n);
cin >> n;
s = fac(n);
cout <<"函数的值为:"<< s;
}
int fac(int n)
{
int s;
if (n==1)
s = n*n;
else
s = n*n + fac(n-1);
return s;
} 12. 三角形的面积为 area=s*(s-a)*(s-b)*(s-c) 其中,s=1/2*(a+b+c), a , b, c 为三角形的三边。定义两个带参数的宏,一个用来求S,另一个用来求 area 。 编写程序,在程序中用带实参的宏名来求面积。
//带实参的宏求三角形面积
#include
#include
using namespace std;
#define S(a,b,c) (a+b+c)/2
#define AREA(a,b,c) sqrt(S(a,b,c)*(S(a,b,c)-a)*(S(a,b,c)-b)*(S(a,b,c)-c))
int main()
{float a,b,c;
cout<<"input a,b,c:";
cin>>a>>b>>c;
if (a+b>c && a+c>b && b+c>a)
cout<<"area="< 这里使用了宏作为简易函数的用法,关于宏用法的总结请见:
https://blog.csdn.net/zl3090/article/details/84750896