DeepLearning | Zero Shot Learning 零样本学习 零样本工业故障诊断

本文是对浙江大学工业过程国家重点实验室赵春晖课题组最新论文：Fault Description Based Attribute Transfer for Zero-Sample Industrial Fault Diagnosis, IEEE TII, 2020 的翻译与解读，全文阅读约10～20分钟。

Abstract

文章提出了一种极具挑战性的故障诊断研究任务，即考虑在没有目标故障样本可用于训练的情况下进行建模。这种情形在工业领域是很普遍的，但之前几乎没有过相关的研究，这限制了传统的数据驱动方法在实际过程中的应用。在文章中，作者将零样本学习的理念引入了工业过程，通过提出基于故障描述的属性迁移方法来解决这一零样本故障诊断任务。

具体来说，该方法学习使用人工定义的故障描述而不是收集的故障样本来确定故障类别。定义的故障描述由故障的一些属性组成，包括故障位置，故障影响，甚至故障的原因等。对于目标故障而言，其相关属性可以从同一工业过程的其余故障的描述中预先学习和迁移得到。接着，便可以在无需其他任何数据训练的情形下，基于定义的故障描述诊断目标故障。另外，论文中的方法采用有监督的主成分分析方法提取与属性相关的特征以提供有效的属性学习。

文章从理论上分析和解释了基于故障描述方法的有效性和可行性。首次基于经典的田纳西-伊斯曼过程和真实的百万千瓦火电过程设计了零样本情形下的故障诊断实验，结果表明在没有样本的情况下诊断目标故障是确实可能的。

关键词：故障诊断，故障描述，机器学习，零样本学习，工业过程，迁移学习

一、Introduction

故障诊断和分类是大型工业维护的重要任务[1]、[2]，为了提高对各种故障的诊断能力，人们提出了大量的数据驱动方法[3]、[4]。传统的基于分类算法的故障诊断包括三个阶段：数据采集、特征提取和故障分类[5]。在第一个数据采集步骤中，工厂会安装许多传感器来收集日常运行中的故障信号。特征提取则通常采用矩阵分解方法[6]、时频分析[7]和卷积神经网络[8]、[9]等来实现降维和去噪。在最后一个分类步骤中，将提取的特征作为输入，得到用于故障诊断的机器学习模型[10]。然而，这三步流程更像是实验室的规则，而不是实践中的期望。因为对于日常流程操作中出现的目标故障，更常见的工业场景是没有或很少有故障数据可用。考虑到许多故障可能具有破坏性并会造成巨大损失，很少有工厂会被允许运行到故障状态并采集样本来训练故障诊断系统[11]。同时，机器通常会经历一个从健康到故障的逐渐退化过程，这也表明为数据驱动方法获取足够的故障样本是费时费力的[12]。

为了克服为某些故障采集样本的困难，一种可接受的方法是将从一些容易获得或历史故障（训练故障）中学到的知识应用于那些难以或昂贵采集的故障（目标故障）[13]、[14]。因此，Lu等人[15] 将深度神经网络与最大均方差项相结合，提出了一种无需目标故障样本的高精度故障诊断深度迁移学习方法。Long等人[16]也使用了稀疏自动编码器 来训练深度域自适应模型。然而，对于深度迁移学习[17]而言，在训练域中已经准备好了与目标故障同样的故障。虽然目标域的故障不需要训练样本，但深度迁移学习实际上解决的是训练域和目标域之间的域偏移问题，而不是文章所考虑的零样本问题。此外，故障树分析[18]、[19]也是一种典型的工业场景分析方法，它根据一些基本故障来诊断系统故障。它被成功地应用于了解系统故障的原因，并找到降低风险的最佳方法，或确认故障的发生率[20]，[21]。然而，当将故障树分析应用于定量分析时，专家系统通常需要基本故障的频率。这意味着某些目标故障的记录（样本）已经准备好，同样也不符合零样本的要求。

最近，Lampert等人[22]在零样本动物识别的任务中提出了新颖的方法。在该任务中，规定测试阶段出现的动物类别是没有训练图片的。Lampert没有直接训练分类算法，而是利用非线性支持向量机来学习动物的属性，即“颜色”和“形状”等，并利用训练好的向量机来预测其他动物（测试类别）的属性。通过这种属性的迁移检测出新的动物。这种方法被称为直接属性预测（DAP）。Lampert等人[23]还从标签中来学习动物属性，提出了间接属性预测（IAP）方法。此外，在零样本学习中，还有利用匹配度函数和平方损失来学习图像与属性之间映射的方法。Akata等人[24]通过找到产生最高相容性得分的标签，对图像进行零样本分类。以及Romera Paredes等人[25]提出了一种非常简单的零样本学习方法，将特征、属性和类之间的关系建模为基于平方损失的两层线性网络。从目标属性中学习目标的零样本学习[26]为零样本故障诊断问题提供了一种可能的解决方案。但是，当它应用到故障诊断任务时，是没有图像可用于获取各种故障的“颜色”或“形状”等属性。这些视觉属性并不适用于工业传感器信号，零样本故障诊断任务需要更有效的辅助信息。

当我们在实践中学习一种新的故障时，首先往往注意到的是故障的特征和语义描述，而不是样本的数值多少。例如，从描述“一种由管道、联轴器和阀门相连，用于输送固体颗粒、气体或液体的装置”，我们可以在根本看不见的情况下认识到“管道”对象。此外，当人们被告知“管道中的流体流动停止或异常缓慢”时，他们知道存在“管道堵塞”故障。因此，用结论良好的描述代替样本来诊断和识别各种故障在直观上是可行的。人为定义的故障描述是故障类别识别的有力信息。工业故障的每一种描述通常包含若干属性，包括故障的影响、故障的位置、故障的原因等。显然，有许多可能的属性，但是，人们定义的属性往往是超越故障类别界限的[22]，[23]。例如，“磨煤机轴承异常振动”故障和“磨煤机盘管温升”故障都发生在“磨煤机”上。我们可以利用现有的训练数据，将“磨煤机”上也出现的其他几种故障类别的样本合并，对“磨煤机”这一属性为了学习和识别，并将这些知识应用于目标故障。人们定义的属性可以被不同的故障共享，这为从不同故障类别的描述中获取属性知识提供了可能。

此外，高维度低密度信息是工业传感器数据的另一个重要特征[27]、[28]。统计特征提取算法[29]，[30]通常被用于有效的数据挖掘和特性揭示。最流行和经典的方法是主成分分析[31]，[32]，它以无监督的方式进行特征提取。大量的案例研究和前人的工作都证明了它的有效性。然而，对于通常在有监督学习范式中定义的故障诊断任务[33]，有监督主成分分析[34]更有助于目标相关特征的提取和有效诊断。

总而言之，文章提出基于故障描述的属性迁移方法，研究了目标故障类别没有训练样本的故障诊断任务。该方法不采用传统的诊断范式，而是为每个故障提供由属性组成的故障描述作为辅助信息。这一故障描述层嵌入在故障样本层和故障类别层之间。基于故障描述层的细粒度类共享属性，构建了一个级联诊断系统，用于将训练故障的属性知识迁移到目标故障进行零样本的故障诊断。在基于故障描述的方法中，我们还采用有监督的主成分分析作为特征提取器，为更有效的学习过程提供与属性相关的特征。

文章的主要贡献总结如下：

 1. 第一次总结了零样本故障诊断任务，尝试在没有样本的情况下诊断目标故障

 2. 提出了以故障描述为辅助知识源的方法，以从训练故障到目标故障进行属性迁移的方式实现了零样本的故障诊断

文章的其余部分安排如下。在第二节中，我们将零样本诊断问题公式化。第三节提出了基于故障描述的属性迁移方法，并对其进行了可行性分析。在第四节中，零样本故障诊断任务和方法在标准的田纳西-伊斯曼过程和真实的火电厂过程上进行验证。最后，我们给出了结论和今后的工作。

二、Problem Formulation

2.1 故障描述在向量空间的配置

如上所述，文章总结了每种故障的故障描述，以提供细粒度的类别信息。描述由任意属性组成，包括故障的影响、故障的位置和故障的原因等。每个属性是向量空间中的一个维度，故障的描述表示为${\mathbf{a}}^{\prime }\in {\mathbb{R}}^{C^{\prime }}$，其中$C^{\prime }$是属性数。对于$L$类故障，描述矩阵可以表示为 $\mathbf{A}\in {\mathbb{R}}^{L\times C^{\prime }}$。

这里采用了独热编码的方法，使 ${\mathbf{A}}^{\prime }$ 变为$\mathbf{A}$稀疏矩阵 $\mathbf{A}\in {\mathbb{R}}^{L\times C}=onehot({\mathbf{A}}^{\prime })$ ，其中$C$是独热热编码的维度。$\mathbf{A}$中的所有元素都是1或0，这表示该属性在某个故障类别的描述中是否存在。

2.2 零样本诊断任务公式化

文章的目标是诊断和识别$p$类故障。目标故障集表示为 $T=\{T_1,\dots ,T_p\}$。但是，我们没有 $T$ 的训练样本。这里有一些其他可用的故障类别，这些类别表示为 $S=\{S_1,\dots ,S_q\}$，其中 $q$ 是可用的故障类别数量，$T$和$S$彼此不相交，即 $T\cap S=\varnothing$。$S$的样本表示为$\Im =\{{\mathbf{X}}_S\in {\mathbb{R}}^{N_S\times D},\mathbf{Y}\in {\mathbb{R}}^{N_S}\}$ , 其中$N_S$是样本数，$D$是特征维度。零样本故障诊断任务需要学习从$S$到$T$之间的映射$f$，其公式如下

Min $CLoss({\mathbf{Y}}_T,{\hat{\mathbf{Y}}}_T)$, and ${\hat{\mathbf{Y}}}_T=f({\mathbf{X}}_S,{\mathbf{Y}}_S|{\mathbf{X}}_T)$······（1）
其中 ${\mathbf{X}}_T$和 ${\mathbf{Y}}_T$表示测试阶段目标故障的样本和标签， $CLoss$表示任意分类损失。

在介绍了$T$和$S$的故障描述$\mathbf{A}$之后，可以将（1）中的目标函数重写为

Min $CLoss({\mathbf{Y}}_T,{\hat{\mathbf{Y}}}_T)$, and ${\hat{\mathbf{Y}}}_T=f({\mathbf{X}}_S,{\mathbf{Y}}_S,\mathbf{A}|{\mathbf{X}}_T)$ ········（2）

其中$\mathbf{A}=[{\mathbf{A}}_S,{\mathbf{A}}_T]\in {\mathbb{R}}^{L\times C}$是属性描述矩阵，$L=p+q$。值得一提的是，$S$的属性描述矩阵${\mathbf{A}}_S$和$T$的属性描述矩阵${\mathbf{A}}_T$都可用于模型训练，因为属性描述是类级别而不是样本级别,是容易获得的公共知识而不是专家知识。

与传统的数据驱动故障诊断问题相比，零样本诊断是一个更有意义和挑战性的任务，其目的是克服为目标故障类别收集大量样本的困难。

三、Methodology

如第二节所述，文章的目标是诊断和分类在训练阶段没有样本的故障。本节首先提出基于故障描述的属性迁移方法，继而给出可行性分析。

3.1 基于故障描述的属性迁移

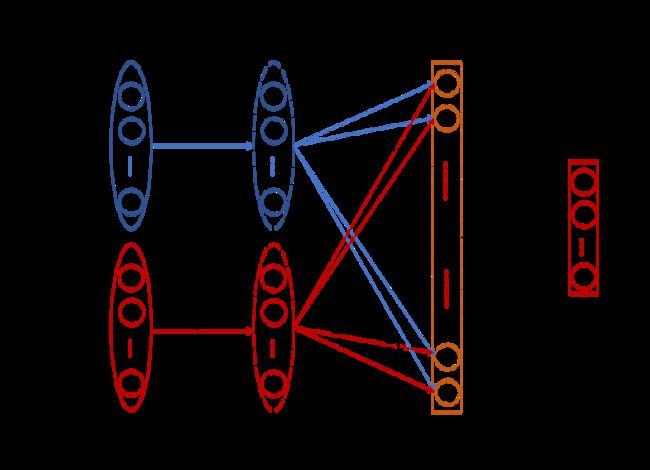
对于一般的机器学习模型，如支持向量机或决策树，它们通常根据故障样本或提取的特征，为每种故障类别学习一个参数向量（或其他表示）${\alpha }_i$来实现分类。显然，由于目标类 $T=\{T_1，\dots ，Tp\}$在训练阶段没有样本，无法为$T$获取参数向量，他们不可能直接实现零样本故障诊断任务的从$S$到$T$学习。图1描述了这种困境

图1.普通机器学习算法在零样本诊断任务中的困境：无法为目标故障获得参数向量

也就是说，为了识别没有训练样本的目标故障，学习系统需要从训练故障中提取与目标故障相关的信息。由于没有目标故障的训练数据，这种耦合不能直接从样本中提取。因此，故障描述$\mathbf{A}$被用来提供额外的辅助信息，并实现从训练故障到目标故障的属性迁移。图2给出了基于故障描述的零样本故障诊断方法的基本思想。

图2. 基于故障描述方法的基本思想。$N$是训练故障的样本数，$N^{\prime }$是测试阶段目标故障的样本数，$\phi$是有监督主成分分析的映射，$\mathbf{b}$是$\mathbf{x}$的特征，${\alpha }_i（i=1,...,C）$是每个属性的属性学习器（回归器或分类器），$a_i(i=1,...,C)$是$\mathbf{A}\in {\mathbb{R}}^{L\times C}$中的属性，$\beta$是从属性描述到目标故障类别的推理规则。

1. 级联模型的第一步是特征提取。 我们拼接训练标签 ${\mathbf{Y}}_S$ 和训练故障的属性描述 ${\mathbf{A}}_S$ 以获取训练故障属性标签 ${\mathbf{Z}}_S=[{\mathbf{z}}_1^S,...,{\mathbf{z}}_C^S{]}^T\in {\mathbb{R}}^{N\times C}$, 这表示每一个故障样本被一个 $C$维的属性向量描述。有监督的主成分分析应用于数据对$\{\mathbf{X}，{\mathbf{z}}_i^S\}（i=1，\dots ，C$，以提取与属性相关的特征。训练样本$\mathbf{x}$的特征表示为$\mathbf{b}$，该特征转换表示为$\phi$。
2. 第二步是基于特征提取的属性学习和迁移阶段。它不直接学习特征和标签之间的映射，而是在训练阶段以监督的方式为每种属性$a_i$训练属性学习器${\alpha }_i（i=1，\dots ，C）$。在测试时，这些属性学习器允许对目标故障的每个测试样本预测属性值（1或0）。注意，只要在训练和目标故障的描述属性维度相同，就不需要针对目标故障提供的额外数据训练。
3. 基于得到的测试样本的属性向量，进行第三步，推断出测试样本的最终故障类别。因为目标故障${\mathbf{A}}_T\in {\mathbb{R}}^{p\times C}$的故障描述是已知的，所以从故障描述到故障类别的推理规则$\beta$有很多，例如最近邻搜索等。

这里，图2中的级联模型也以概率的方式来描述以获得准确的表示。特征$\mathbf{b}$通过转换映射$\phi$从样本$\mathbf{x}$中提取。从特征到故障描述进行推理的第二步可以表示为$p(\mathbf{a}|\mathbf{b})={\prod }_{i=1}^{C}p(a_i|\mathbf{b})$，其中$\mathbf{a}\in {\mathbb{R}}^C$是$\mathbf{A}$中一种故障的属性描述。这里，第$t$类的属性向量$\mathbf{a}$表示为${\mathbf{a}}^t=[a_1^t,...,a_C^t]$。基于Bayes规则，我们将推理表示为

$p(t|\mathbf{a})={\sum }_{t=1}^p\frac{p({\mathbf{a}}^t|t)p(t)}{p({\mathbf{a}}^t)}[\mathbf{a}={\mathbf{a}}^t]$ ·················（3）
如果 $\mathbf{a}={\mathbf{a}}^t$， $[\mathbf{a}={\mathbf{a}}^t]=1$， 否则它为 0. 由于属性描述矩阵 ${\mathbf{A}}_T$ 是已知的, 我们有 $p({\mathbf{a}}^t|t)=1$. 在缺少明确信息的情况下, 类别先验概率 $p(t)$ 被认为是等同的. 对于 $p({\mathbf{a}}^t)={\prod }_{i=1}^{C}p(a_i^t)$, 训练集的经验均值 $p(a_i^t)=\frac{1}{q}{\sum }_{j=1}^q{a}_i^{s_j}$ 被使用. 将上述三步组合，一个样本的故障类别后验概率可以以如下的方式得到
$p(t|\mathbf{x})=p(t|\mathbf{a})p(\mathbf{a}|\mathbf{b})=\frac{p(t)}{p({\mathbf{a}}^t)}{\prod }_{i=1}^{C}p(a_i^t|\mathbf{b})$ ················（4）
其中 $\mathbf{b}=\phi (\mathbf{x})$。为了从所有的故障类别 $t_1,...,t_p$ 中为一个测试样本 $\mathbf{x}$挑选出最可能的故障类别，可以使用最大概率估计的方法
$f(\mathbf{x})={\mathrm{argmax}}_{j=1,...,p}{\prod }_{i=1}^C\frac{p(a_i^{t_j}|\phi (\mathbf{x}))}{p(a_i^{t_j})}={\mathrm{argmax}}_{j=1,...,p}\frac{p({\mathbf{a}}^{t_j}|\mathbf{b})}{p({\mathbf{a}}^{t_j})}$ ··········（5）
其中 ${\mathbf{a}}^{t_j}$ 表示第 $j$种 目标故障的属性描述向量， ${\mathbf{a}}_i^{t_j}$ 是 ${\mathbf{a}}^{t_j}$的第 $i$个元素. 方程（5）揭示了基于描述的方法实际上是在 特征$\mathbf{b}$和故障描述$\mathbf{a}$之间进行故障诊断。因此，故障特征和描述对于零样本任务至关重要。

3.2 方法的可行性分析

令${\mathbf{X}}_S=[{\mathbf{x}}_1^S,...,{\mathbf{x}}_N^S]$ 和 ${\mathbf{X}}_T=[{\mathbf{x}}_1^T,...,{\mathbf{x}}_{N^{\prime }}^T]$ 表示训练故障和目标故障的样本。 ${\mathbf{B}}_S=[{\mathbf{b}}_1^S,...,{\mathbf{b}}_N^S]$ 和 ${\mathbf{B}}_T=[{\mathbf{b}}_1^T,...,{\mathbf{b}}_{N^{\prime }}^T]$ 是相应的特征, ${\mathbf{Y}}_S\in {\mathbb{R}}^N$ 和 ${\mathbf{Y}}_T\in {\mathbb{R}}^{N^{\prime }}$ 是他们的标签。 $\mathbf{A}=[{\mathbf{A}}_S,{\mathbf{A}}_T]\in {\mathbb{R}}^{L\times C}$ 表示每一种故障由一个 $C$维的属性向量描述, 因此我们可以通过拼接 $\mathbf{A}$ 与 ${\mathbf{Y}}_S$ 和 ${\mathbf{Y}}_T$ 得到属性标签${\mathbf{Z}}_S=[{\mathbf{z}}_1^S,...,{\mathbf{z}}_N^S]\in {\mathbb{R}}^{N\times C}$ 和 ${\mathbf{Z}}_T=[{\mathbf{z}}_1^T,...,{\mathbf{z}}_{N^{\prime }}^T]\in {\mathbb{R}}^{N^{\prime }\times C}$。不失一般性的，训练和目标故障类别的属性学习器 $g_S=\{{\alpha }_1^S,...,{\alpha }_C^S\}$ 和 $g_T=\{{\alpha }_1^T,...,{\alpha }_C^T\}$ 分别表示从特征 ${\mathbf{B}}_S$ 和 ${\mathbf{B}}_T$ 到属性标签 ${\mathbf{Z}}_S$ 和 ${\mathbf{Z}}_T$ 的线性映射。

所提出的基于故障描述方法的迁移技巧在图二中的第二步。这里训练故障的属性学习器$g_S$ 被用作目标故障的属性学习器 $g_T$. 这里，我们分析这种迁移使用属性学习器的可行性，即 $g=g_S=g_T$。

定义： 对于 $\forall {\mathbf{b}}_i^T$, 假设 $\exists {\mathbf{u}}_i\in {\mathbb{R}}^N$， ${\mathbf{b}}_i^T={\mathbf{u}}_i{\mathbf{B}}_S$. 相似的, 对于 $\forall {\mathbf{z}}_i^T$, $\exists {\mathbf{v}}_i\in {\mathbb{R}}^N$, ${\mathbf{z}}_i^T={\mathbf{v}}_i{\mathbf{Z}}_S$。集合 $U=\{{\mathbf{u}}_i\}$ 和 $V=\{{\mathbf{v}}_i\}$ 是 ${\mathbf{B}}_T$和${\mathbf{Z}}_T$对于${\mathbf{B}}_S$ 和 ${\mathbf{Z}}_S$的相关知识。

特征$\mathbf{B}$和属性标签$\mathbf{Z}$都是对故障的描述。相关知识$U$实际上是${\mathbf{B}}_T$对于${\mathbf{B}}_S$在特征空间内依赖的编码。$V$是${\mathbf{Z}}_T$对于${\mathbf{Z}}_S$在属性标签空间内依赖的编码。基于相关知识的定义，我们可以得到关于属性学习器共享的引理。

引理: 如果 $\forall j$, ${\mathbf{u}}_j={\mathbf{v}}_j$, 从训练故障样本$\{({\mathbf{b}}_i^S,{\mathbf{z}}_i^S)\}$中学习得到的映射 $g_S:{\mathbf{b}}^S\to {\mathbf{z}}^S$ 可以被直接用做 $g_T:{\mathbf{b}}^T\to {\mathbf{z}}^T$ 为测试目标故障类别样本 $\{({\mathbf{b}}_i^T,{\mathbf{z}}_i^T)\}$进行预测。

证明：令 ${\mathbf{b}}_j^T={\sum }_{i=1}^N{\mathbf{u}}_j{\mathbf{b}}_i^S$, 有 $g_S({\mathbf{b}}_j^T)=g_S({\sum }_{i=1}^N{\mathbf{u}}_j{\mathbf{b}}_i^S)$ $={\mathbf{u}}_j{\sum }_{i=1}^N{g}_S({\mathbf{b}}_i^S)={\mathbf{v}}_j{\sum }_{i=1}^N{\mathbf{z}}_i^S={\mathbf{z}}_j^T=g_T({\mathbf{b}}_j^T)$。

因此，根据引理，当关系知识$U$和$V$相等时，在线性情况下，属性学习器的共享是完全可行的。直观地讲，特征空间中的关系知识$U$是由训练样本和目标故障类别共同决定的，并且是不可改变的。然而，属性标签空间中的关系知识$V$是由定义的$\mathbf{A}$决定的，它可以从故障描述中学习并通过反复试验加以提升。

四、Case Studies

本节提供两个案例研究。一个是使用田纳西-伊斯曼基准流程设计的。为了更好地理解所提出的零样本故障诊断任务和方法，文章在这一充分研究的数据集上详细介绍了实验设置和模型实现。另一个是在实际的火电厂过程中，展示了基于故障描述的属性迁移方法的应用。

4.1 田纳西-伊斯曼基准过程

4.1.1 数据集介绍

由Downs和Vogel[35]、[36]贡献的田纳西-伊斯曼过程（TEP）是一个在工业上得到充分研究的故障诊断数据集，它有助于公正地呈现新提出的零样本诊断任务和基于故障描述的属性转移方法的有效性。此外，我们还提供了用于实验的TEP的细粒度属性描述，以显示零样本故障诊断任务的辅助信息。

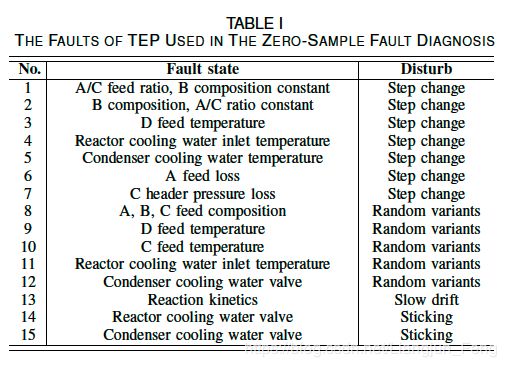
TEP由五个主要子系统组成，包括反应器、冷凝器、气液分离器、循环压缩机和产品汽提器。数据集提供了21种故障，每种故障由41个测量变量和11个操作变量描述。采集480个样本，对每个故障进行训练。由于最后6种故障在数据集中的描述较少，本文利用前15种故障进行零样本故障诊断实验。表一介绍了15种故障类型，所研究的15种故障类型各不相同。当其中一些模型训练样本为零时，传统的故障诊断方法很难进行故障诊断。因此，提出的零样本故障诊断方法具有实际意义和实用价值。

4.1.2 模型实现

故障描述是提出零样本故障诊断方法的基础。图3显示了TEP在向量空间中的属性描述的配置，即属性矩阵$\mathbf{A}$，具体的属性名如表二所示。每种故障都由20个细粒度属性描述。对比表二和表一，应该注意的是，属性描述可以从表一的语句中很容易得出。根据故障描述，我们可以在诊断目标故障时不需要使用其样本进行模型训练。

TEP数据集的故障描述矩阵A。每种故障都由20个细粒度属性描述。图中的“1”表示故障有这个属性，“0”表示没有。属性的具体名称见表二。

图2中基于描述的方法的第一步是特征提取。采用监督主成分分析法提取属性相关特征。具体地说，每对 $\{{\mathbf{X}}_S,{\mathbf{z}}_i^S\}(i=1,...,C)$都由监督主成分分析进行拟合[34]。然后将提取器应用于测试数据${\mathbf{X}}_T$。对于每个属性，从原始的52个变量中提取20个特征。由于有20个不同的属性，在特征提取之后，将为以下步骤准备一个包含400个特征的数据集。第二步是属性学习器的训练。文章采用了三种不同的机器学习算法，包括线性支持向量机（LSVM）、非线性随机森林（RF）和概率朴素贝叶斯（NB）。具体采用的是scikit learn[37]的实现对三个模型进行了公平的比较。LSVM的松弛项参数设为1，RF的决策树数设为50。最后，使用最近邻搜索作为推理规则来确定最终的故障类别，并使用普通欧氏距离。

TEP采用15种故障，训练/测试故障数量采用80%-20%的划分，即12种故障作为训练故障，3种故障作为目标故障。为了测试整个数据集的性能，将TEP数据集分为5组，每组有3个测试故障和12个训练故障。训练/测试划分见表三，训练样本数为5760（12480），测试样本数为1440（3480）。我们报告了五组实验的准确率。

4.1.3 零样本诊断结果

零样本故障诊断结果见表四，最高诊断精度随训练/测试划分的变化而变化，从62.63%到88.40%。五组实验的最佳结果的混淆矩阵如图4所示。

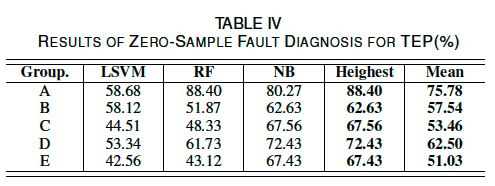
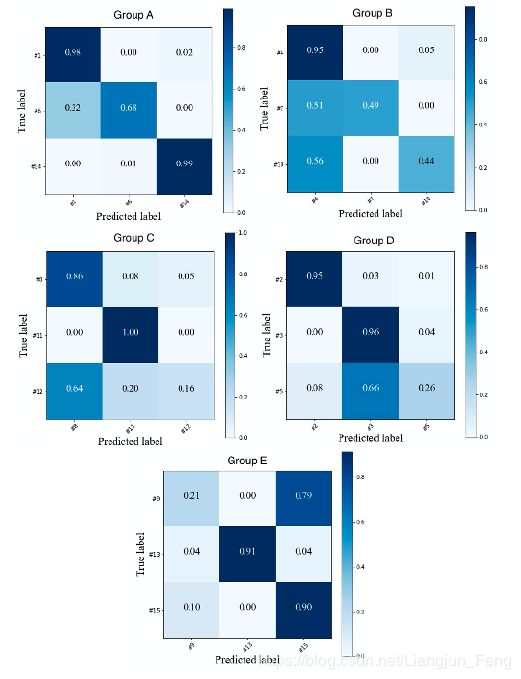
图4. TEP数据集5组实验结果的混淆矩阵

显然，基于故障描述的属性转移方法的性能明显高于33.33%的随机水平，这证明了基于故障描述的故障诊断方法的初衷：在没有训练样本的情况下，基于人工定义的故障描述可以对不同类型的故障进行诊断和分类。对于某些特定故障类别的准确度，如图4中D组的26%和E组的21%，它们是由于零样本任务的困难造成的，下一小节中的少样本实验将表明我们的结果实际上是相当有竞争力的。此外，值得一提的是，虽然对属性学习器共享的可行性的证明仅限于线性情况，但非线性分类器和概率分类器（即RF和NB）的较高性能表明，该方法是普遍适用的。

据作者所知，没有一种基于数据驱动的方法能够在没有样本进行模型训练的情况下实现故障诊断和分类。如前所述，典型的技术，包括深度转移学习和故障树分析，不适用于零样本故障诊断设置。因此，为了提供相同设置下的比较，Lampert等人提出的零样本学习方法，即DAP和IAP[22]、[23]，被使用进行对比。注意，DAP和IAP是为图像分类任务而设计的，Lampert设计的“形状”或“颜色”属性不能在这里使用，而是使用本文总结的故障描述。图像特征，即HoG和SIFT，在这里也不适用。我们让DAP和IAP从原始数据中学习。将DAP和IAP的非线性支持向量机（高斯核）的松弛项设为1。因此，比较实际上是基于我们的贡献，即故障描述。虽然DAP和我们方法的思想都是属性转移，但是我们的方法利用了不同的属性学习器和特征。结果如表5所示。当线性LSVM被设置为属性学习器时，我们的方法通过5组DAP和IAP呈现出具有竞争力的精度。当利用非线性属性学习器RF和概率属性学习器NB时，该方法获得了更高的精度。同时，我们尝试将我们的方法与Akata等人的SJE[24]和Romera Paredes等人的ESZSL[25]进行比较。然而，由于卷积网络的深层特征以及SJE和ESZSL所要求的基于图像的属性在故障诊断场景下都是不可用的，它们的性能在B、C、E组上都存在严重的退化，这表明它们在工业场景下的泛化能力弱，难以实现零样本故障诊断任务。

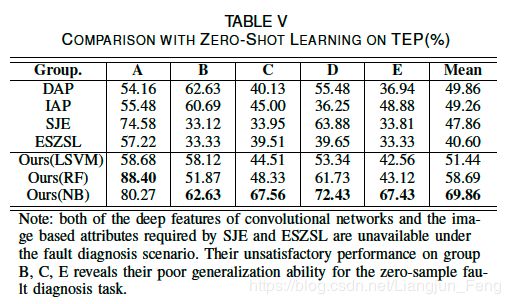
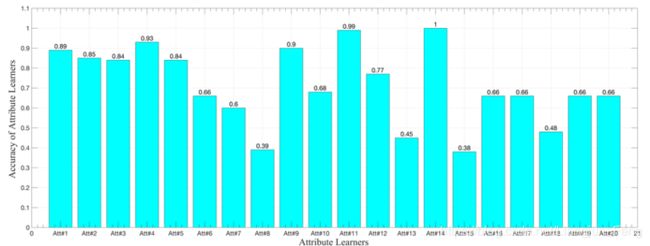
另一个需要评估的性能是属性学习器的准确性，这是零样本故障诊断的基础。在我们的方法中，模型先学习故障属性，然后才知道故障。以RF为属性学习器的A组20个属性学习器的准确度如图5所示。大多数属性学习器的学习效果比随机猜测（50%的准确率）要好得多，其中一些属性学习器对A组的准确率甚至达到90%以上，这直接说明了所提出的基于故障描述的方法的有效性。

图5. 以RF为属性学习器的A组20个属性学习器的准确率。

4.1.4 与少样本学习的比较

为了比较，我们还进行了基于A组和C组的少量样本学习实验，其中1、10、50、200、500个样本用于模型训练。训练样本是从TEP的另一组数据中随机抽取的，测试数据与零样本故障诊断数据相同。比较的算法包括LSVM、RF、NB、XGBoost（XGB）[38]、AdaBoost（ADA）、K-邻域（KNN）、梯度增强机（GBDT）[39]和轻量梯度增强机（LGBM）[40]。对于所有被比较的模型，他们的作者或scikit学习包[37]的实现被用于公平的比较。实验中使用的scikit-learn包的LSVM模型对于多类分类问题默认采用“1-v-1”策略。在参数方面，我们统一采用了作者的默认设置，不做任何调整，这通常表现出良好的性能。少数样本学习实验的结果如表六和表七所示。

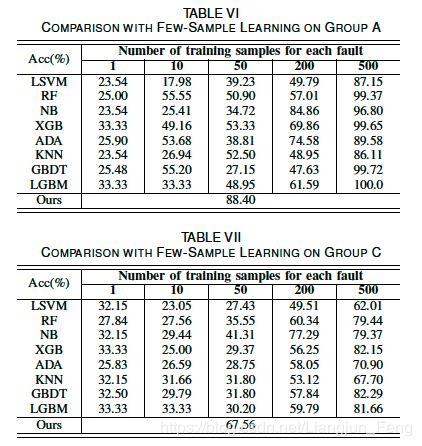
如表六和表七所示，传统的机器学习算法在只提供少量故障样本的情况下性能较差，其中一些算法使用一个样本时的性能甚至比随机选择（33.33%）还要差。尽管TEP是一个经过充分研究的经典故障诊断数据集，但与我们的方法相比，比较方法至少还需要200个样本来呈现竞争性的结果，这说明了零样本故障诊断任务的难度。实际上，由于零样本设置和一个样本设置是完全不同的，而且难度更大，因此我们的方法与少数样本学习相比是不公平的。这说明故障描述确实为诊断提供了额外的故障信息。

4.1.5 对噪声的鲁棒性

噪声是工业生产过程中普遍存在的典型干扰。为此，对该方法进行了噪声实验，证明了该方法的鲁棒性。将所增加的噪声分配给均值为零、变化方差的高斯分布。属性学习采用NB。结果见表八

通常，当噪声方差小于0.5时，该方法表现良好。当噪声方差大于0.5时，性能下降。有时，当噪声方差为0.3时，系统的性能会更好，例如在A组上的性能。提出的方法对故障的识别是基于对属性的认识的。如表8所示，在噪声环境下，A组和C组20个属性学习器的平均精度都是稳定的，这有助于获得零样本任务的鲁棒结果。

4.2 火电站过程

4.2.1 数据集介绍

火力发电厂（TPP）故障数据集是从1000mw超超临界火电机组的实际工业过程中获取的。热力过程由锅炉系统和汽轮机系统两个主要子系统组成。

图6. 火电站过程系统结构图

在发电过程中，锅炉系统首先将水加热成高温高压蒸汽。然后蒸汽被输送到涡轮系统来驱动发电机。整个动力装置实现了从化学能到电能的转换。由于火力发电是一个大规模的过程，机组停机采集故障样本会造成巨大的损失。因此，在零样本条件下诊断某些故障类别具有重要意义。

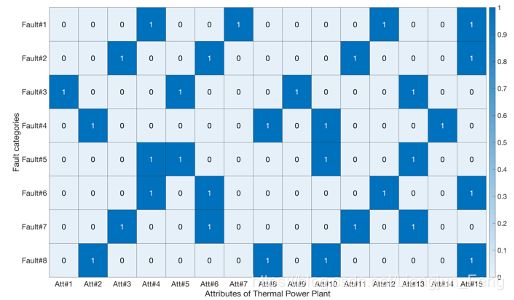
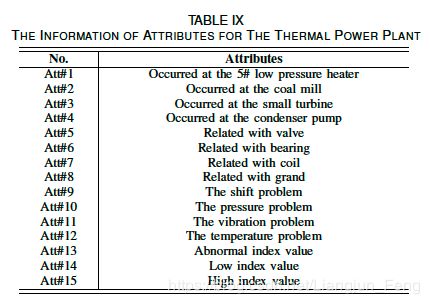
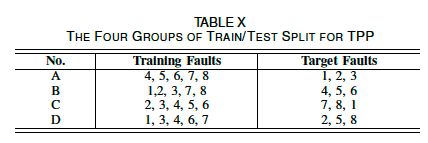
图7. TPP的故障描述矩阵A。每种故障都是由15个细粒度属性描述。图中的“1”表示故障有这个属性，“0”表示没有。属性的具体名称如表九所示。

数据集提供了八种发生在整个机组上的故障。每种故障由68个实测信号和4320个样本进行了说明。用15种属性描述故障。火力发电厂数据集的故障描述矩阵$\mathbf{A}$如图7所示，具体的属性信息如表9所示。为了测试所提出的基于故障描述的属性转换方法的稳健性，采用四组不同的训练/测试划分，如表10所示，每组包括五种模型训练故障和三种测试故障。模型实现与TEP相同。

4.2.2 零样本诊断结果

火电厂过程零样本故障诊断结果见表十一。四组实验的最佳结果的混淆矩阵如图8所示。一般情况下，TPP的零样本故障诊断结果远高于TEP。

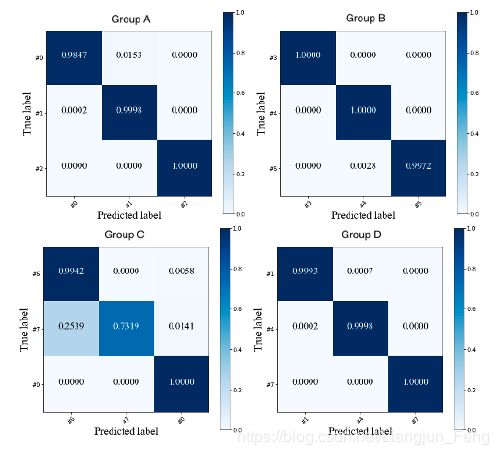
图8. 火电站过程4组实验结果的混淆矩阵

四组平均准确率为85.07%～94.93%，TEP为51.03%～75.78%。这可以用故障描述矩阵$\mathbf{A}$来解释。与TEP相比，火力发电厂过程的$\mathbf{A}$定义揭示了更详细的信息。例如，表九提供了具体的过程变量，即“温度”、“压力”和“振动”，以及过程变量的具体特性，即“低”和“高”。该方法可以方便地从传感器信号中提取细节信息，并应用于属性的准确识别。因此，LSVM、RF和NB这三种机器学习算法都能在目标故障上获得良好的性能。以RF为属性学习者的A组的15个属性学习者的准确度如图9所示。

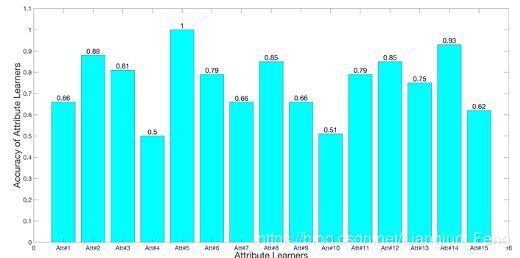
图9. 火电站过程A组15名属性学习器RF的准确率

以RF为属性学习器的A组20个属性学习器的平均准确率为71.45%，TPP为75.06%。这验证了所提出的基于故障描述的属性迁移方法的有效性，该方法首先学习故障描述和属性，然后对故障进行诊断。此外，由于火电厂过程中的许多机器是旋转机器，如涡轮机、发电机和卷取机，因此该过程通常在噪声环境下工作。因此，表11和图9所示的高性能也验证了所提出方法的鲁棒性和模型现实的匹配。

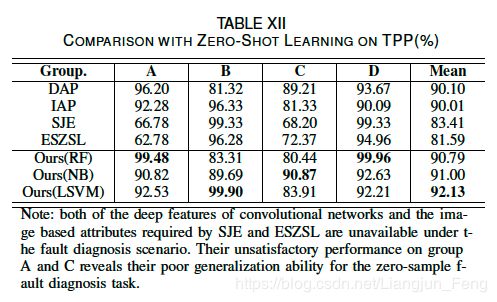
并与其他零样本学习方法进行了比较。实验设置与TEP相同。结果见表十二。对于火电厂过程，线性LSVM通过四个不同的组表现出较高的平均精度，揭示了过程的线性特征。SJE和ESZSL在组A和组B上表现出不稳定的性能，因为设计的深度特征在这里是不适用的。此外，DAP和IAP与我们的相比精度较低。DAP在实验中直接从故障样本中学习，而设计的模型则通过有监督的主成分分析来学习与属性相关的特征。由于DAP和我们的方法都是基于属性转移的，因此结果可以揭示特征对于零样本故障诊断任务的重要性。

五、Conclusions

考虑到故障样本采集的困难，本文提出了零样本故障诊断任务。设计了基于故障描述的属性迁移方法，首次尝试在没有样本的情况下诊断目标故障。与基准数据集上的少量样本学习相比，该方法具有目标故障样本数为零的优点。对实际火电厂过程的高精度分析和可行性分析也表明，通过设计合理的故障属性描述，确实可以实现零样本诊断。在今后的研究中，还有许多工作可以进一步发展和完善。例如：（1）可以考虑零样本诊断的解决方案，即使用一些流行的生成模型，即生成-对抗网络，根据故障描述为目标故障生成样本；（2）在本文中，利用有监督的主成分分析方法作为零样本诊断中提取属性相关特征的基本方法，可以开发出更有意义和可解释性的方法来更好地执行任务。

六、References

1. Y. Ma, S. Bing, H. Shi, et al. Fault detection via local and nonlocal embedding, Chemical Engineering Research & Design, vol. 94, pp.538-548, 2015.
2. Q. Liu, S. J. Qin, T. Chai, Decentralized fault diagnosis of continuous annealing processes based on multilevel PCA, IEEE Trans. Automation Science & Engineering, vol. 10, no. 3, pp. 687-698, 2013.
3. W. Fan, T. Shuai, Y. Yang, et al, Hidden Markov model-based fault detection approach for multimode process, Industrial & Engineering Chemistry Research, vol. 55, no. 16, pp. 4613-4621, 2016.
4. S. Zhao, B. Huang, L. Fei, Fault detection and diagnosis of multiple-model systems with mismodeled transition probabilities, IEEE Trans. Industrial Electronics, vol. 62, no. 8, pp. 5063-5071, 2015.
5. Q. Liu, Q. Q. Zhu, S. J. Qin, etc. Dynamic concurrent kernel CCA for strip-thickness relevant fault diagnosis of continuous annealing processes, J. Process Control, vol. 67, 2017.
6. G. Xin, H. Jian. An improved SVM integrated GS-PCA fault diagnosis approach of Tennessee Eastman process, Neurocomputing, vol. 32, pp. 1023-1034, 2015.
7. X. Q. Deng, X. M. Tian, X. Y. Hu. Nonlinear process fault diagnosis based on slow feature analysis, in Proc. Intelligent Control and Automation, 2012.
8. L. Cui, N. Wu, W. Wang, et al., Sensor-based vibration signal feature extraction using an improved composite dictionary matching pursuit algorithm, Sensors, vol. 14, no. 9, pp. 16715-16739, 2014.
9. L. Eren, T. Ince, and S. Kiranyaz, A generic intelligent bearing fault diagnosis system using compact adaptive 1D CNN classifier, Journal of Signal Processing Systems, vol. 91, no. 2, pp. 179-189, 2019.
10. Y. L. Murphey, M. A. Masrur, Z. H. Chen, etc., Model-based fault diagnosis in electric drives using machine learning, IEEE/ASME Transactions on Mechatronics, vol. 11, no. 3, pp. 290-303, 2006.
11. C. Sun, M. Ma, Z. Zhao, et al., Deep transfer learning based on sparse auto-encoder for remaining useful life prediction of tool in manufacturing, IEEE Trans. Industrial Informatics, vol. 15. No. 4, pp. 2416-2425, 2018.
12. J. Zhao, D. T. Ouyang, X. Y. Wang, et al., The modeling procedures for model-based diagnosis of slowly changing fault in hybrid system, Advanced Materials Research, vol. 186, pp. 403-407, 2011.
13. Y. Pan, F. Mei, H. Miao, et al., An approach for HVCB mechanical fault diagnosis based on a deep belief network and a transfer learning strategy, Journal of Electrical Engin. & Techn., vol. 14, no. 1, pp. 407-419, 2019.
14. S. S. Yu, M. A. Stephen, Y. Ruqiang, et al., Highly-accurate machine fault diagnosis using deep transfer learning, IEEE Trans. Industrial Informatics, vol. 15, no. 4, pp. 2446-2455, 2019.
15. W. Long, G. Liang, and X. Li, A new deep transfer learning based on sparse auto-encoder for fault diagnosis, IEEE Trans. Systems Man & Cybernetics Systems, vol. 49, no. 1, pp. 136-144, 2018.
16. W. Lu, B. Liang, Y. Cheng, et al., Deep model based domain adaptation for fault diagnosis, IEEE Trans. Ind. Electron., vol.64, no.3, pp. 2296-2305, 2017.
17. S. J. Pan, Q. Yang, A survey on transfer learning, IEEE Trans. Knowledge & Data Engineering, vol. 22, no.10, pp.1345-1359.
18. W. S. Lee, D. L. Grosh, F. A. Tillman, et al. Fault tree analysis, methods, and application: a review, IEEE Trans. Reliability, vol. 34, no.3, pp.194-203, 2009.
19. A. K. Reay, J. D. Andrews. A fault tree analysis strategy using binary decision diagrams, Reliability Engineering & System Safety, vol. 78, no. 1, pp. 45-56, 2002.
20. R. M. Sinnamon, J. D. Andrews, Improved efficiency in qualitative fault tree analysis, Quality & Reliability Engineering International, vol. 13, no. 5, pp. 293-298, 1997.
21. C. Samir, Fault tree analysis, John Wiley & Sons, Inc. 2006.
22. C. H. Lampert, H. Nickisch, and S. Harmeling. Learning to detect unseen object classes by between-class attribute transfer, in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Jun. 2009, pp. 951-958.
23. C. H. Lampert, H. Nickisch, and S. Harmeling, Attribute-based classification for zero-shot visual object categorization, IEEE Trans. Pattern Anal. Mach. Intell., vol. 36, no. 3, pp. 453-465, Mar. 2014.
24. Z. Akata, S. Reed, and D. Walter, et al. Evaluation of output embeddings for fine-grained image classification, in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Jun. 2015.
25. B. Romera-Paredes and P. H. Torr, An embarrassingly simple approach to zero-shot learning, in Proc. Int. Conf. Machine Learning, 2015.
26. S. Kang, D. Lee, C. D. Yoo. Face attribute classification using attribute-aware correlation map and gated convolutional neural networks, in Proc. IEEE International Conference on Image Processing, 2015.
27. C. H. Zhao, Y. X. Sun, Comprehensive subspace decomposition and isolation of principal reconstruction directions for online fault diagnosis, Journal of Northwest A & F University, vol. 23, no. 10, pp. 1515-1527, 2013.
28. C. H. Zhao, F. R. Gao, Fault subspace selection approach combined with analysis of relative changes for reconstruction modeling and multifault diagnosis, IEEE Trans. on Control Systems Technology, vol. 24, no. 3, pp. 1-12, 2015.
29. J. C. Wang, Y. B. Zhang, et al. Dimension reduction method of independent component analysis for process monitoring based on minimum mean square error, J. Process Control, vol. 22, no. 2, pp. 477-487, 2012
30. C. H. Zhao, W. Q. Li, Y. X. Sun, A sub-principal component of fault detection modeling method and its application to online fault diagnosis, in Proc. the 9th Asian Control Conference. 2013.
31. J. H. Chen, C. M. Liao, et al., Principle component analysis based control charts with memory effect for process monitoring, Industrial & Engineering Chemistry Research, vol. 40, no .6, pp. 1516-1527, 2001.
32. M. Misra, H. H. Yue, S. J. Qin, etc. Multivariate process monitoring and fault diagnosis by multi-scale PCA, Computers & Chemical Engineering, vol. 26, no. 9, pp. 1281-1293, 2002.
33. M. Li, X. Wu, Fault diagnosis for fans of coal based on CBR hybrid threshold method, in Proc. Int. Conf. Fuzzy Systems and Knowledge Discovery, 2010.
34. E. Barshan, A. Ghodsi, Z. Azimifar, et al. Supervised principal component analysis: Visualization, classification and regression on subspaces and submanifolds,’’ Pattern Recognition, vol. 44, no. 7, pp.1357-1371, 2011.
35. J. J. Downs, E. F. Vogel, A plant-wide industrial process control problem, Computers & Chemical Engineering, vol. 17, no. 3, pp. 245-255, 1993.
36. W. Yu, and C. Zhao, Online fault diagnosis in industrial process using multi-model exponential discriminant analysis algorithm, IEEE Trans. Control Systems Technology, vol. 27, no. 3, pp. 13317-1325, 2018.
37. S. Ashish, J. Ritesh, Scikit-learn: machine learning in python, Journal of Machine Learning Research, vol. 12, no.10 pp. 2825-2830, 2012.
38. T. Q. Chen, C. Guestrin, XGBoost: a scalable tree boosting system, in Proc. the 22nd ACM SIGKDD, 2016, pp. 785-794.
39. H. J. Friedman. Greedy function approximation: a gradient boosting machine, Annals of Statistics, vol. 29, no. 5, pp. 1189-1232.
40. G. L. Ke, M. Qi, et al. LightGBM: a highly efficient gradient boosting decision tree. Advances in Neural Information Processing Systems, 2017, pp. 3149-3157.

资源下载

微信搜索“老和山算法指南”获取各类论文代码下载链接与技术交流群

有问题可以私信博主，点赞关注的一般都会回复，一起努力，谢谢支持。