图网络算法——基础图论

图网络算法——基础图论

1、图基础

1.1、图的基本结构

一般情况下。一个图的组成包括点的集合和边的集合。表示为$G(N,E)$其中N表示点的集合，E表示边的集合。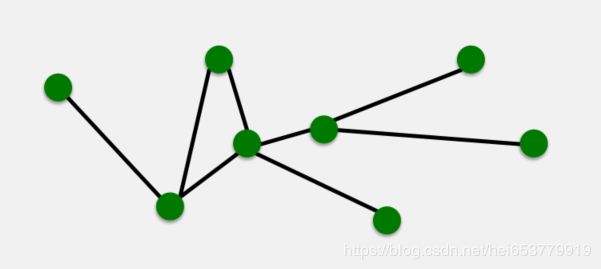
如上图所示，绿色的点构成了节点集合N，黑色的边构成了边的集合E。整张图表示成$G(N,E)$。

1.2、 如何理解图和网络？

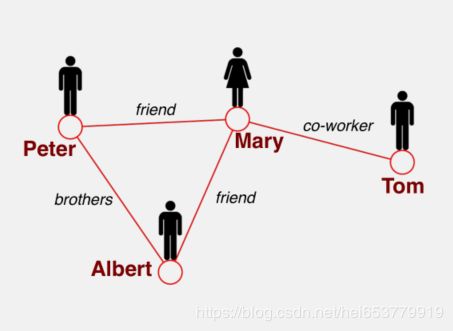
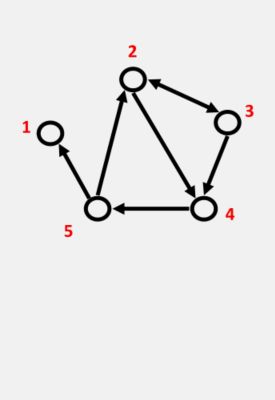
对于一个网络而言，其反应的是一个真实的系统，例如我们可以将一个人的社会关系抽象成一个网络。对于图而言，其是网络的一种数学表示。在网络中，节点和边有具体的表示，例如节点表示一个人，边表示两个人之间的关系。而对于图，图中的节点和边没有实际的意义表示，更多的是一种数学表达。如下面的两个图来表示：

1.3、图有哪些分类？

1.4.1、有向图和无向图

无向图： 在一个图中，如果边是没有方向的，那么这个图被称为无向图。

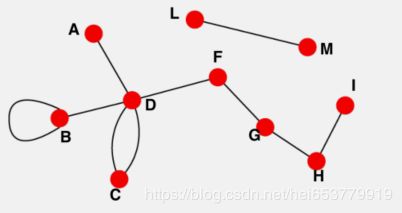
在实际的应用中，例如人际关系，社交网络等可以抽象成一个无向图。

有向图： 在一个图中，如果边是有方向的，那么这个图被称为是有向图。

在实际中，例如疾病和药物之间的关系可以构建出一个有向图。

1.3.2 无向图和有向图的节点的度

首先，我们先来确定一下度的概念。

在无向图中：

度： 对于无向图而言，节点的度指的是与节点相连的边的个数。对于整个图而言，其平均的度为：
$$K^{-}=<K>=\frac{1}{N}\sum _{i=1}^N{K}_i=\frac{2E}{N}$$

在有向图中：

出度： 是指有某个点发出的边的个数。
入度： 是指指向某个点的边的个数。
对于整个有向图而言，其度为：
$$K^{-}=\frac{E}{N}$$

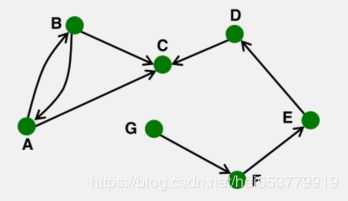
我们下面举两个例子来计算一下：

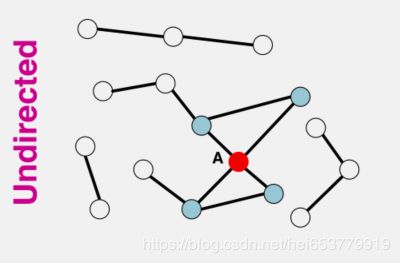对于无向图中的节点A而言，其度$K_A=4$。

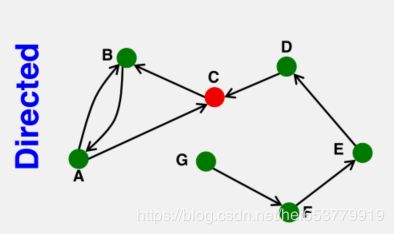对于有向图而言，节点C的入度为$K_C^{in}=2，K_C^{out}=1，K_C=3$。

1.4 完全图

在一张无向图中，如果图中的任意两个节点之间都有边连接，则该图可以成为完全图(complete graph)。对于一个完全图而言，其边的个数为：
$$E=E_{max}=\frac{N(N-1)}{2}$$
其中N表示图中的所有的节点的个数。E表示图中所有边的个数。在完全图中，每个节点的度为(N-1)。

1.5 二分图

这是一类比较特殊的二分图，该图中的节点可以分成两个部分U和V，其中U和V是独立，也就是和V的交集为一个空集。并且，图中的所有的边连接的都是两个部分的节点。每个部分的内部是没有边连接的。如下图所示：

在现实生活中，演员——电影，观众——电影等都可以抽象出一个二分图的结构。

1.5.1、二分图的折叠和投影

通过一个二分图结构，我们可以进一步对其进行折叠操作，所谓的折叠，就是通过另外一个部分来推断当前节点的关系。举个例子来说，在上面的二分图中，我们可以将整个图拆分成关于U和V的两个子图。

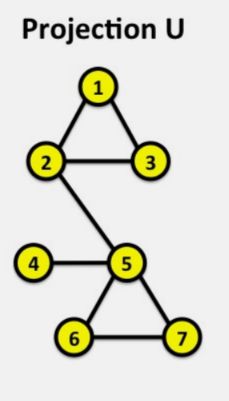
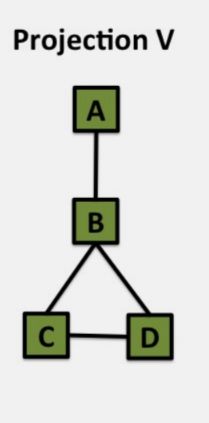
以第一个图为例，根据U和V中的节点连接，U中连接到V同一个节点的不同节点具有关系。所有构成了左图的部分，同时根据相同的原理构成了右图的部分。

对于图的投影，就是折叠的逆过程，将两个子图合并成一个二分图，如最上面所示。

1.6 其他的图类型

1.6.1 权重图和无权重图

我们以网页引用作为一个例子，在现实世界中，一个网页$i$被不同的网页$j$引用的次数是不同的，也就是说，当图中的边表示引用关系的时候，不同的边根据引用次数不同，边也应该是不同的。而对于一个朋友关系的网络中，如果人i和不同的人j之间是存在朋友关系，显然，这种朋友关系显然是没有优劣之分的，也就是如果两个节点之间存在着边，就可以说明两个节点之间存在朋友关系。

对于上面的描述，我们很自然的就引出啦有权重图和无权重图，有权重图指的就是图中的边具有一个权重值，无权重图指的就是图中连接的节点之间的边是没有权重的。如下图所示：

1.6.2 自连接图、多关系图、连通图

所谓的自连接图，指的就是在一个图中存在某个节点i指向自身的边。所谓的多关系图，指的就是图中的某些节点之间存在着多条边进行连接。连通图指的是在图中的任意两个节点$i,j$之间都存在着路径。如下图所示：

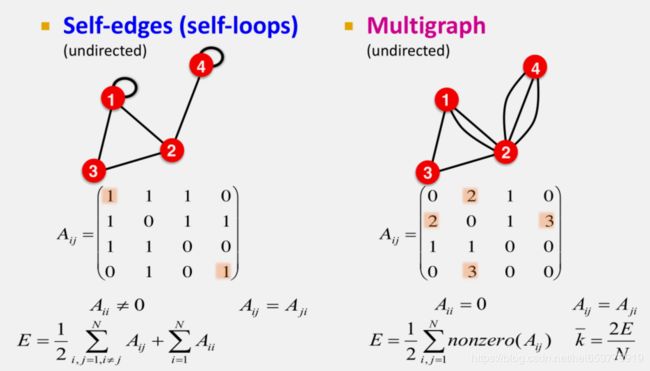
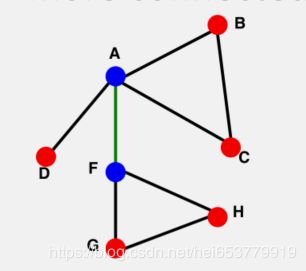
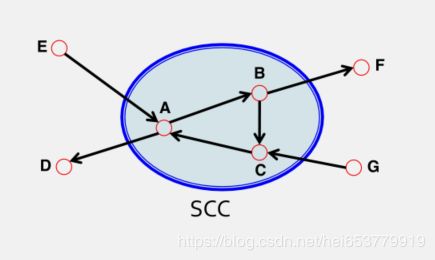
对于有向图而言，其连通图可以进一步分成强连通图和弱连通图。强连通图(SCC)指的是两个节点AB之间，即存在从A到B的路径，也存在从B到A的路径，而弱连通图指的是AB之间值存在从A到B的路径或者从B到A的路径。如下图所示。

1.7 图表示

1.7.1 邻接矩阵表示

通常情况下，我们采用邻接矩阵来对于整个图进行表示，所谓的邻接矩阵，每一个行和每一列表示的是图中的一个节点。每一个元素表示行列节点是否具有连接，如果有连接则值为1，否则值为0。如下图所示：

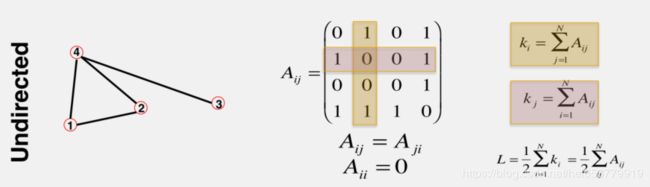
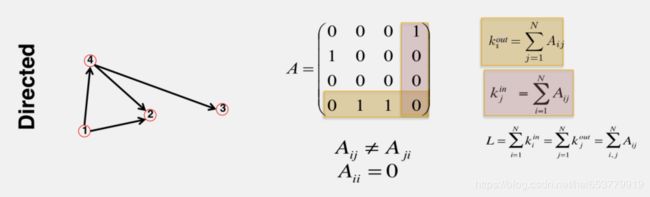在现实情况中，邻接矩阵一般是稀疏矩阵，如果采用上面的邻接矩阵的表示方式，则显然会对空间造成巨大的浪费。所以，为了节省空间，下面介绍根据边的表示方式。

1.7.2 基本边的表示方式

这种表示方式的思路比较简单，对于图中存在边连接的两个节点i,j。我们采用根据边的关系，以二元祖的形式进行保存，最终获得一个二元组的集合，如下图所示：

1.7.3 邻接表

这种表示方式，结合了上面的两种方式，既可以表示大的图，也可以表示边比较稀疏的图，其基本构建流程是，首先按照节点序号构建一个节点数组，在以指针的方式，如果两个节点i,j之间存在边，则在数组中该节点i的后面指向一个j节点。如下图所示：