Go语言应用:广度优先算法走迷宫
广度优先算法(Breadth-First Search),同广度优先搜索,又称作宽度优先搜索,或横向优先搜索,简称BFS,是一种图形搜索演算法。简单的说,BFS是从根节点开始,沿着树的宽度遍历树的节点,如果发现目标,则演算终止。广度优先搜索的实现一般采用open-closed表。
实现目标:
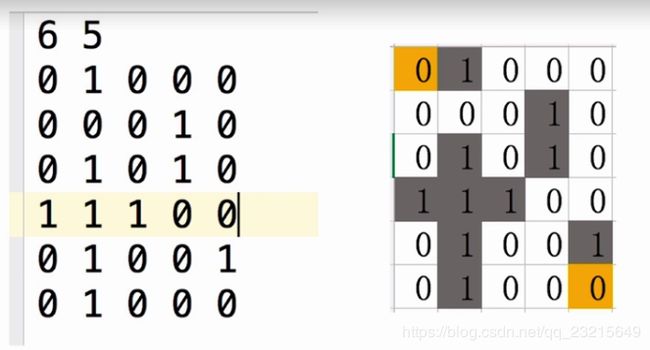
使用go语言实现广度优先算法走如下图的迷宫,使路线最短:
(第一行两数分别表示行数和列数,0代表路,1代表墙,从左上角进,右下角出)
原理分析:
经过观察总结可知,有三种类型的点。
类型一:
已经发现,但未探索过得点。
类型二:
已经发现,且探索过得点。
类型三:
尚未发现的点。
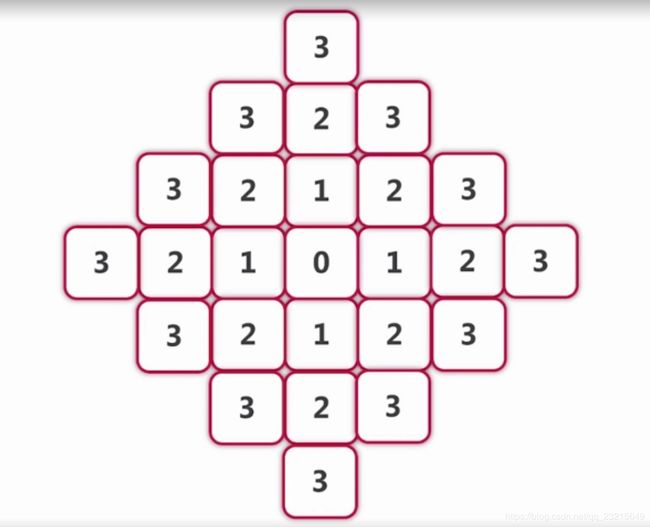
我们需要先探索标号为1的点,结束后对标号为二的点进行探索,以此类推,逐层往外探索。因此类型一的点尤其重要,我们需要对其进行入队(FIFO)。
通过对迷宫实际推演,我们可以得到以下步骤即为路径最短的走法:
结束条件:
1:找到出口。
2:带探索的点队列为空。
分步实现:
第一步:获取迷宫信息
//首先需要对文件进行读取,获取迷宫信息。
func readMaze(filename string) [][]int {
file ,err := os.Open(filename)
if err != nil{
panic(err)
}
var row,col int
fmt.Fscanf(file,"%d %d",&row,&col)
maze := make([][]int,row)
//一共有row行
for i := range maze{
maze[i] = make([]int,col)
//循环遍历行,得到j
for j:= range maze[i] {
fmt.Fscanf(file, "%d", &maze[i][j])
}
}
return maze
}func main(){
maze := readMaze("src/maze/maze.in")
for _,row := range maze{
for _,val := range row{
fmt.Printf("%d",val)
}
fmt.Println()
}
}通过readMaze()函数可以获得文件中的迷宫信息。
运行结果如下:
00100
00000
10000
01001
11000
01000
Process finished with exit code 0实现广度优先算法:
type point struct{
i,j int
}
//探索地图,不指定出口入口
func walk(maze [][]int,start,end point) [][]int {
steps := make([][]int,len(maze))
for i := range steps{
steps[i] = make([]int,len(maze[i]))
}
Q := []point{start}
for len(Q) > 0 {
cur := Q[0]
Q =Q[1:]
if cur == end{
break
}
for _,dir := range dirs{
next := cur.add(dir)
//maze at next is 0
val,ok:= next.at(maze)
if !ok || val ==1{
continue
}
//and steps next is 0
val,ok = next.at(steps)
if !ok || val != 0{
continue
}
//and next!= start
if next == start {
continue
}
curSteps,_ := cur.at(steps)
steps[next.i][next.j] = curSteps + 1
Q = append(Q,next)
Q = append(Q)
}
}
return steps
}
var dirs = [4]point{
{-1,0},{0,-1},{1,0},{0,1}}
//代替运算符重载
func (p point) add(r point) point{
return point{p.i + r.i,p.j+r.j}
}
func (p point) at(grid [][]int) (int,bool){
if p.i <0 || p.j >= len(grid){
return 0,false
}
if p.j < 0 || p.j >= len(grid[p.i]){
return 0,false
}
return grid[p.i][p.j],true
}
最中代码为:
package main
import (
"os"
"fmt"
)
func main() {
maze := readMaze("src/maze/maze.in") //读maze.in文件
//验证读取是否正确
for _,row := range maze{
for _,val := range row{
fmt.Printf("%3d ",val)
}
fmt.Println()
}
fmt.Println("--------")
steps :=walk(maze,point{0,0},point{len(maze)-1,len(maze[0])-1})
//打印走的路径
for _,row := range steps{
for _,val := range row{
fmt.Printf("%3d ",val)
}
fmt.Println()
}
}
type point struct {
i,j int
}
//走的路径,指下一个方向
var dirs = []point{
{-1,0},{0,-1},{1,0},{0,1}}
func (p point)add(r point) point {
return point{p.i+r.i,p.j+r.j}
}
//获取点point在grid位置的值
func (p point)at(grid [][]int) (int,bool){
if p.i < 0 || p.i >= len(grid){
return 0,false
}
if p.j < 0 || p.j >=len(grid[p.i]){
return 0,false
}
return grid[p.i][p.j],true
}
func walk(maze [][]int,start,end point) [][]int{
steps := make([][]int,len(maze))
for i := range steps{
steps[i] = make([]int,len(maze[i]))
}
Q := []point{start}
for len(Q) > 0{
cur := Q[0]
Q = Q[1:]//切片,去掉cur,依次循环下去cur都不是以前的值
if cur == end{
break
}
for _,dir := range dirs{
next := cur.add(dir)
//maze at next is 0
//and steps at next is 0
//and next != start
val,ok := next.at(maze)
if !ok || val == 1{
continue
}
val,ok = next.at(steps)
if !ok || val != 0{
continue
}
if next == start{
continue
}
curSteps,_ := cur.at(steps)
steps[next.i][next.j] = curSteps + 1
Q = append(Q,next)
}
}
return steps
}
func readMaze(filename string) [][]int {
file,err := os.Open(filename)
if err != nil{
panic(err)
}
var row,col int
fmt.Fscanf(file,"%d %d",&row,&col) //读取文件第一行两个数并跟据row、col的地址,将其赋值
fmt.Println("row:",row,"col:",col) //row: 6 col: 5
/* 测试fmt.Fscanf函数
fmt.Fscanf(file,"%d",&row)
fmt.Print("row:",row)//row:6
fmt.Fscanf(file,"%d",&ces)
fmt.Print("ces:",ces)//ces:0,换行会变为0
*/
maze := make([][]int,row)//声明一个row行的二维切片
for i:=range maze{
maze[i] = make([]int,col)
for j:= range maze[i]{
_,err := fmt.Fscanf(file,"%d",&maze[i][j])
//其中文件中换行符会导致error,所以采用以下方式多读取一行
if err!=nil && err.Error() == "unexpected newline"{
fmt.Fscanf(file, "%d")
}
}
}
return maze
}结果为:
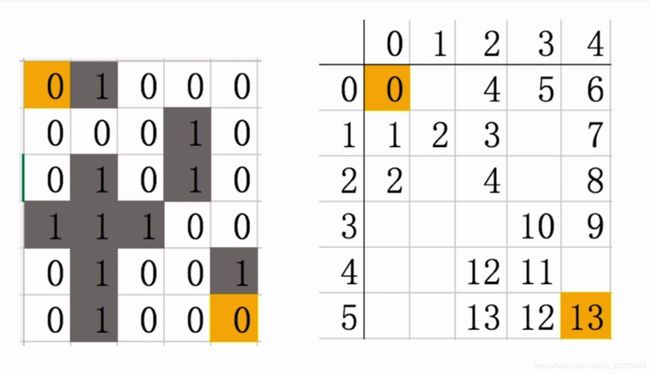
row: 6 col: 5
0 1 0 0 0
0 0 0 1 0
0 1 0 1 0
0 1 1 0 0
0 1 0 0 1
0 1 0 0 0
--------
0 0 4 5 6
1 2 3 0 7
2 0 4 0 8
3 0 0 10 9
4 0 12 11 0
5 0 13 12 13