朴素贝叶斯分类
文章目录
- 应用
- 贝叶斯公式
- 朴素贝叶斯分类器
- 半朴素贝叶斯分类器
- 独依赖估计
- 多属性依赖
前面我们了解全概率公式和贝叶斯公式,如果对贝叶斯公式不太熟悉可以参考 全概率公式与贝叶斯公式这篇文章。
应用
- 中文分词 分词后,得分的假设是基于两词之间是独立的,后词的出现与前词无关
- 统计机器翻译 统计机器翻译因为其简单,无需手动添加规则,迅速成为了机器翻译的事实标准。
- 贝叶斯图像识别 首先是视觉系统提取图形的边角特征,然后使用这些特征自底向上地激活高层的抽象概念,然后使用一个自顶向下的验证来比较到底哪个概念最佳地解释了观察到的图像。
贝叶斯公式
首先复习一下贝叶斯公式:
假设有事件A, B i , i = 1 , 2 , 3 , . . . , n \quad B_i,i=1,2,3,...,n Bi,i=1,2,3,...,n,则在A事件发生时, B i B_i Bi事件发生的概率 P ( B i ∣ A ) P\left(B_{i} | A\right) P(Bi∣A):
P ( B i ∣ A ) = P ( B i A ) P ( A ) = P ( B i ) P ( A ∣ B i ) P ( A ) P\left(B_{i} | A\right)=\frac{P\left(B_{i} A\right)}{P(A)}=\frac{P(B_i)P(A|B_i)}{P(A)} P(Bi∣A)=P(A)P(BiA)=P(A)P(Bi)P(A∣Bi)
现在我们可以将上述公式应用于分类问题,求出样本 x \bm x x在各个类别上发生的最大概率,就可以判断它属于那哪一个类。为了便于我们理解,上述公式可以写成: P ( c ∣ x ) = P ( c ) P ( x , c ) P ( x ) P(c | \boldsymbol{x})=\frac{P(c)P(\boldsymbol{x}, c)}{P(\boldsymbol{x})} P(c∣x)=P(x)P(c)P(x,c)
其中 Y = { c 1 , c 2 , … , c N } , \mathcal{Y}=\left\{c_{1}, c_{2}, \dots, c_{N}\right\}, Y={c1,c2,…,cN}, c 表 示 类 别 , Y 表 示 数 据 集 中 类 的 集 合 , x \quad c表示类别,\mathcal{Y}表示数据集中类的集合,\bm x c表示类别,Y表示数据集中类的集合,x表示数据集中的一个样本(是一个多维向量,每一维代表一个属性)。
- P ( c ) P(c) P(c)是先验概率,代表整个数据集中是c类的概率,可用频率代替,即 ∣ c ∣ ∣ Y ∣ \frac{|c|}{|\mathcal{Y}|} ∣Y∣∣c∣.
- 由全概率公式得 P ( x ) = ∑ j = 1 n P ( c j ) P ( x ∣ c j ) P(\bm x)= { \sum _ { j = 1 } ^ { n } P \left(c_j\right) P \left( \bm x | c_j \right) } P(x)=∑j=1nP(cj)P(x∣cj),对于所有的样本结果相同,称为证据因子,与类别标记无关。因此在贝叶斯分类过程中可以分母去掉。
- P ( x ∣ c ) P(\bm x|c) P(x∣c)是样本 x \bm x x相对于类别c的类条件概率。表示c类中有 x \bm x x的概率。
朴素贝叶斯分类器
通常情况下,样本 x \bm x x都有多种属性, P ( c ∣ x ) P(c|x) P(c∣x)是样本 x \bm x x所有属性上的联合概率,难以从有限的样本中直接估计而得,为了避开这个障碍,朴素贝叶斯采用了属性条件独立性假设,假设每个属性独立的对分类结果产生影响,即计算每种属性是某一类的概率 P ( c ∣ x i ) P(c|x_i) P(c∣xi)( x i x_i xi表示样本 x \bm x x的某种属性),然后将样本x的所有属性是某类的概率相乘 Π i = 1 d P ( c ∣ x i ) \Pi_{i=1}^d{P(c|x_i)} Πi=1dP(c∣xi),然后比较属于每个类的概率谁大。
以下公式中 c c c代表样本集合 Y \mathcal Y Y中的一个类。
因此贝叶斯公式可以写成:
P ( c ∣ x ) = P ( c ) P ( x ∣ c ) P ( x ) = P ( c ) P ( x ) ∏ i = 1 d P ( x i ∣ c ) P(c | \boldsymbol{x})=\frac{P(c) P(\boldsymbol{x} | c)}{P(\boldsymbol{x})}=\frac{P(c)}{P(\boldsymbol{x})} \prod_{i=1}^{d} P\left(x_{i} | c\right) P(c∣x)=P(x)P(c)P(x∣c)=P(x)P(c)i=1∏dP(xi∣c)
,因为 P ( x ) P(\bm x) P(x)对所有的类别都相同,所以我们不需要考虑这一项,因此贝叶斯分类可以改写成:
h n b ( x ) = a r g m a x c ∈ Y P ( c ) ∗ Π i = 1 d P ( x i ∣ c ) h_{nb}(\bm x)={arg max}_{c\in \mathcal{Y}}\quad P(c)*\Pi_{i=1}^dP(x_i|c) hnb(x)=argmaxc∈YP(c)∗Πi=1dP(xi∣c)
若样本充足, P ( c ) P(c) P(c)的概率可以用频率近似, P ( c ) = ∣ c ∣ ∣ Y ∣ P(c)=\frac{|c|}{\mathcal{|Y|}} P(c)=∣Y∣∣c∣, ∣ c ∣ \quad |c| ∣c∣表示 c 类 在 Y c类在\mathcal Y c类在Y中的个数, ∣ Y ∣ \mathcal {|Y|} ∣Y∣表示总个数。
求 ( x i ∣ c ) (x_i|c) (xi∣c)(各个类中 x i x_i xi属性的出现的概率)需要考虑离散型属性和连续型属性值的概率的计算。
- 对于离散型属性,我们可以使用频率近似,即:
P ( x i ∣ c ) = ∣ c x i ∣ ∣ c ∣ , 其 中 ∣ c ∣ 表 示 c 类 的 个 数 , ∣ c x i ∣ 表 示 c 类 中 有 x i 属 性 的 样 本 的 个 数 。 P(x_i|c)=\frac{|c_{x_i}|}{|c|},\\其中|c|表示c类的个数,|c_{x_i}|表示c类中有x_i属性的样本的个数。 P(xi∣c)=∣c∣∣cxi∣,其中∣c∣表示c类的个数,∣cxi∣表示c类中有xi属性的样本的个数。 - 对于连续型属性。首先要考虑概率密度函数,估计样本符合哪种概率密度函数,假设该属性符合正态分布,则:
p ( x i ∣ c ) = 1 2 π σ c , i exp ( − ( x i − μ c , i ) 2 2 σ c , i 2 ) μ , σ 2 表 示 属 性 在 c 类 的 第 i 个 属 性 上 的 均 值 和 方 差 ( 还 可 以 使 用 极 大 似 然 估 计 求 得 ) 。 p\left(x_{i} | c\right)=\frac{1}{\sqrt{2 \pi} \sigma_{c, i}} \exp \left(-\frac{\left(x_{i}-\mu_{c, i}\right)^{2}}{2 \sigma_{c, i}^{2}}\right)\\\mu,\sigma^2表示属性在c类的第i个属性上的均值和方差(还可以使用极大似然估计求得)。 p(xi∣c)=2πσc,i1exp(−2σc,i2(xi−μc,i)2)μ,σ2表示属性在c类的第i个属性上的均值和方差(还可以使用极大似然估计求得)。
举例:
给出样本:
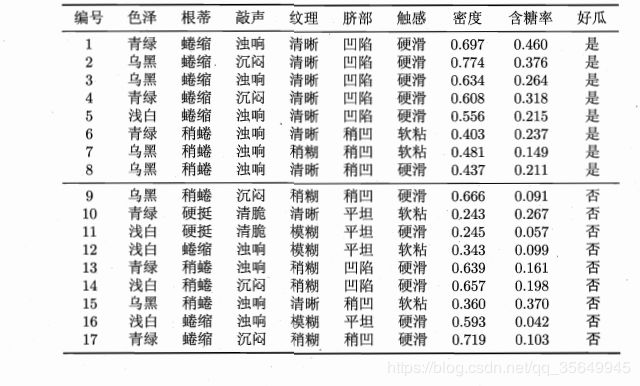
测试样本进行分类:




在计算 h n b ( x ) = a r g m a x c ∈ Y P ( c ) ∗ Π i = 1 d P ( x i ∣ c ) h_{nb}(\bm x)={arg max}_{c\in \mathcal{Y}}\quad P(c)*\Pi_{i=1}^dP(x_i|c) hnb(x)=argmaxc∈YP(c)∗Πi=1dP(xi∣c),我们会发现假如某一个属性值在c类中的个数为零,那么 P ( x i ∣ c ) P(x_i|c) P(xi∣c)=0,由于连乘,将会影响使最终的概率值为零,这使得其他属性对样本的作用为零,显然不符合实际情况,为了避免这种情况出现,我们在求得离散型属性值时可以稍微更改一下求概率公式:
P ( c ) = ∣ c ∣ + 1 ∣ Y ∣ + N P(c)=\frac{|c|+1}{|\mathcal Y|+N} P(c)=∣Y∣+N∣c∣+1
P ( x i ∣ c ) = ∣ c x i + 1 ∣ ∣ c ∣ + N P(x_i|c)=\frac{|c_{x_i}+1|}{|c|+N} P(xi∣c)=∣c∣+N∣cxi+1∣,N表示 x i x_i xi属性的可能取值(例,西瓜的颜色:青绿,浅白,乌黑,则N=3), ∣ c x i ∣ |c_{x_i}| ∣cxi∣表示 x i x_i xi属性在c类中的个数,+1为了避免出现零的情况。这个操作称为拉普拉斯修正。
半朴素贝叶斯分类器
朴素贝叶斯分类不考虑属性间的依赖关系,即属性条件独立性假设;而多数情况下,属性间是有依赖关系的,半贝叶斯是考虑一部分属性间的强依赖关系。
独依赖估计
独依赖估计仅考虑每个属性在类别之外最多仅依赖于一个其他属性。即
h n b ( x ) = a r g m a x c ∈ Y P ( c ) ∗ Π i = 1 d P ( x i ∣ c , p a i ) h_{nb}(\bm x)={arg max}_{c\in \mathcal{Y}}\quad P(c)*\Pi_{i=1}^dP(x_i|c,pa_i) hnb(x)=argmaxc∈YP(c)∗Πi=1dP(xi∣c,pai)
其中 p a i pa_i pai是属性 x x x所依赖的属性,是 x i x_i xi的父属性, P ( x i ∣ c , p a i ) P(x_i|c,pa_i) P(xi∣c,pai)表示属于c类且属性为 p a i pa_i pai的样本有属性 x i x_i xi的概率,可以通过前面条件概率的计算方式求得: P ( x i ∣ c ) = ∣ c x i ∣ ∣ c p a i ∣ , 其 中 ∣ c p a i ∣ 表 示 c 类 中 有 p a i 属 性 的 样 本 的 个 数 。 P(x_i|c)=\frac{|c_{x_i}|}{|c_{pa_i}|},其中|c_{pa_i}|表示c类中有pa_i属性的样本的个数。 P(xi∣c)=∣cpai∣∣cxi∣,其中∣cpai∣表示c类中有pai属性的样本的个数。
现在的问题如何确定属性间的依赖关系,确定每个属性的父属性。
确定父属性的方法有SPODE,TAN,AODE等方法。
多属性依赖
相比于独依赖(一对一属性依赖),多属性依赖是指一个属性可以影响多属性,或者多个属性影响一个属性,这种情况可以用贝叶斯网络来解决。
贝叶斯网络借助于带权有向无环图来表示属性间的依赖关系。假设属性 x i x_i xi的父节点集合是 π i \pi_i πi(即 π i \pi_i πi中的属性决定属性x),则 θ x i ∣ π i = P ( x i ∣ π i ) \theta_{x_i|\pi_i}=P(x_i|\pi_i) θxi∣πi=P(xi∣πi), θ \theta θ定量的描述属性间的关系。
假设贝叶斯网络 B B B由结构 G G G和参数 θ \theta θ构成, B = < G , θ > B=<G,\theta> B=<G,θ>,G是有向无环图。顶点表示属性。若顶点之间有依赖关系,则用有有向线段连接起来。
B = < G , θ > 将 属 性 x 1 , x 2 , . . . x d B=<G,\theta>将属性x_1,x_2,...x_d B=<G,θ>将属性x1,x2,...xd的联合概率分布定义为:
P B ( x 1 , x 2 , x 3 , . . . x d ) = Π i = 1 d P B ( x i ∣ π i ) = Π i = 1 d θ x i ∣ π i P_B(x_1,x_2,x_3,...x_d)=\Pi_{i=1}^dP_B(x_i|\pi_i)=\Pi_{i=1}^d\theta_{x_i|\pi_i} PB(x1,x2,x3,...xd)=Πi=1dPB(xi∣πi)=Πi=1dθxi∣πi
举例:
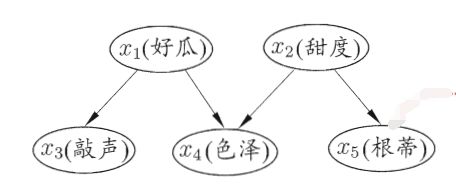
P ( x 1 , x 2 , x 3 , x 4 , x 5 ) = P ( x 1 ) P ( x 2 ) P ( x 3 ∣ x 1 ) P ( x 4 ∣ x 1 , x 2 ) P ( x 5 ∣ x 2 ) P\left(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right)=P\left(x_{1}\right) P\left(x_{2}\right) P\left(x_{3} | x_{1}\right) P\left(x_{4} | x_{1}, x_{2}\right) P\left(x_{5} | x_{2}\right) P(x1,x2,x3,x4,x5)=P(x1)P(x2)P(x3∣x1)P(x4∣x1,x2)P(x5∣x2)