通俗点聊聊算法 - 排序（3）快速排序，亲测

这些天做题的时候吃了不少 快速排序不熟的亏，我痛下决心，一定要自己写出快速排序的几种实现方法！

1、什么是快速排序

快速排序是很重要的算法，和傅里叶变化等算法并称二十世纪最伟大的十大算法。

快速排序的核心思维就是“分而治之”，就像封建王朝的“分封制”。将一大块“领土”，依据“嫡庶长幼”，分为不同部分，各个部分在自行细分，直到分无可分之后，便等级森严了。

说白点，就是在序列中找个元素充当中间量，大的往后，小的往前，一分为二，二分为四，四分为八···

那么，快速排序的技术核心，便呼之欲出了。其一就是这个中间量怎么找，其二就是怎么移动各个元素。

---

2、基准元素的选择

这个元素的选择啊，并不是说要遵循什么准则，你可以选序列头，序列尾，序列中间元素，都可以。
不过选完之后把基准元素放到序列头的位置。

为了简单，后面我就直接选首元素了。

---

3、元素的分配

3.1双边遍历

这个方法呢，如果对快慢指针和双指针不是很了解的朋友可以现在了解一下。

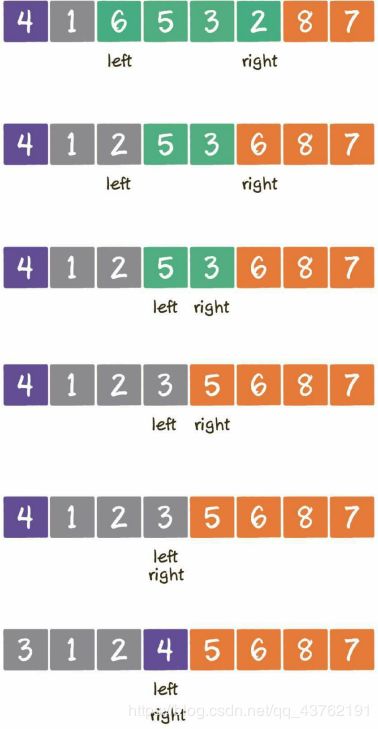
首先啊，确定基准为4，左指针指向第一个元素，右指针指向尾巴。

右指针开始，向前遍历，找到第一个大于基准的元素就停下，轮到左指针，同理。

当两个指针都停下之后，将两个指针所指向的值互换位置。

重复上述步骤直到左右指针重合。

重合之后，将基准元素与左右指针当前位置元素进行互换。

一次循环之后，重复上述动作，对划分出的部分再次循环，直到每个部分都只有一个元素为止。

3.2 单边遍历

这个是快慢指针实现。

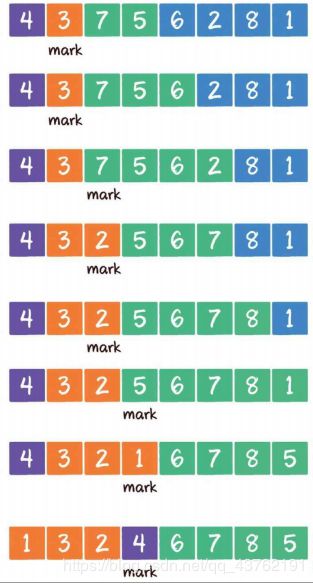
这个mark，是慢指针。快指针没标出来。，依旧找好了基准，快指针从慢指针后一位开始快速遍历，直到遍历到小于基准元素的元素时停滞。

将慢指针前移一位，将当前快慢指针位置元素互换（如果重叠就算了）。然后快指针继续向后走。

重复上述步骤直到左右指针重合。

重合之后，将基准元素与左右指针当前位置元素进行互换。

一次循环之后，重复上述动作，对划分出的部分再次循环，直到每个部分都只有一个元素为止。

---

4、代码实现

以下代码现场手写，如果有什么纰漏还望不吝赐教。

4.1双边循环代码实现

不好意思一段简单代码写了一晚上，不过我已经初步测试好了。

如果有要测试/调试的朋友，我可以讲一下我的调试思路：

先对两个数据进行一次调试，因为这是最后一道坎，这个要是有问题，后面都是白费。
然后·对三个数据进行测试，相信有了前面的基础这个测试会比较顺利。
然后四个数据，五个数据，越来越顺利。我测到六个数据之后便不再测试了，看它没什么情况发生。

如果你有兴趣，建议你去拿其他人的代码测试，他们是把递归和归并分开的，反正我用了几个别人的代码来测试，全崩了。

#include
#include

using namespace std;

void doubleSideSort(vector<int> &vec1,int left,int right)	//序列与左右指针传入
{
	//结束语
	if (right == left)
		return;

	//基准确定
	int flag = vec1[left];

	int keep_right = right;
	int keep_left = left;
	int change_temp;

	//当左右指针还没重合
	while (left<right)
	{
		//左指针先走
		while (left<right && vec1[left]<=flag)
		{
			left++;
		}//当遇到比基准大的数，停下来

		//轮到右指针走
		while (left < right && vec1[right] >= flag)	//可以都等，反正最后都会归并
		{
			right--;
		}//当遇到比基准小的数，停下来

		if (left < right)
		{
			change_temp = vec1[left];
			vec1[left] = vec1[right];
			vec1[right] = change_temp;
		}

		//然后继续循环
	}

	//left--;

	//接着将基准放进去，此时必定是左右相合，则左值若大于左值左边一位，和左值左边一位换，若小，则和左值换
	if (vec1[left] > vec1[left - 1])
	{
		vec1[keep_left] = vec1[left-1];
		vec1[left-1] = flag;
	}
	else
	{
		vec1[keep_left] = vec1[left];
		vec1[left] = flag;
	}

	doubleSideSort(vec1,0,left-1);
	doubleSideSort(vec1, right, keep_right);
}

int main()
{
	vector<int> vec1 = { 4,6,8,7,9,3,1};	//测试用2个数测试最直观，因为最后都要通过这一步才能正常
	int left = 0;
	int right = vec1.size() - 1;

	doubleSideSort(vec1, left, right);

	for (; left <= right; left++)
		cout << vec1[left] << " ";
	cout << endl;

	return 0;
	
}

4.2单边循环代码实现

快慢指针我还是比较有信心的，所以我就测试了四组数据。
如果有任何问题，欢迎留言。

void oneSideSort(vector<int>& vec1, int slow, int hight)
{
	//设置退出条件
	if (slow >= hight)
		return;

	//将标志位留住
	int flag = vec1[slow];

	int keep_slow = slow;
	int keep_hight = hight;

	//使用快指针遍历，将小于标志位的前移
	for (int quick = slow + 1; quick <= hight; quick++)
	{ 
		if (vec1[quick] < flag)
		{ 
			slow++;
			int change_temp = vec1[slow];
			vec1[slow] = vec1[quick];
			vec1[quick] = change_temp;
		} 
	}
	vec1[keep_slow] = vec1[slow];
	vec1[slow] = flag;

	oneSideSort(vec1, keep_slow,slow-1);
	oneSideSort(vec1,slow+1, keep_hight);
}

int main()
{
	vector<int> vec1 = {2,1,2,3};	//测试用2个数测试最直观，因为最后都要通过这一步才能正常
	int left = 0;
	int right = vec1.size() - 1;

	oneSideSort(vec1, left, right);

	for (; left <= right; left++)
		cout << vec1[left] << " ";
	cout << endl;

	return 0;
	
}

稍后还有事儿，就写到这儿啦。