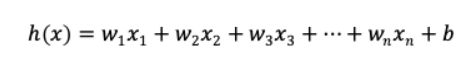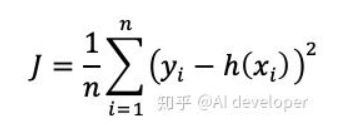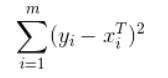机器学习实战（一）线性回归和局部加权线性回归

一、什么是线性回归(Linear Regression)

维基百科：线性回归
在统计学中，线性回归是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。

二、线性回归的数学推导

1.线性回归模型形如：

• 注：线性回归得出的模型不一定是一条直线，在只有一个变量的时候，模型是平面中的一条直线；有两个变量的时候，模型是空间中的一个平面；有更多变量时，模型将是更高维的。
• 实际上，线性回归中通常使用残差平方和，即点到直线的平行于y轴的距离而不用垂线距离，残差平方和除以样本量n就是均方误差。均方误差作为线性回归模型的代价函数(cosfunction)。使所有点到直线的距离之和最小，就是使均方误差最小化，这个方法叫做最小二乘法。

2.代价函数：

3.偏导数法

• 偏导数法是非常麻烦的，需要一个一个地计算w。为了方便，这里以单变量线性回归为例。

4.正规方程法

• 正规方程使用矩阵运算，可以一次求出W向量。但是当变量(feature)个数大于数据个数时，会导致xTx不可逆，这时候就不能用此方法了。
• 使用正规方程法，如果希望得到的模型带有偏置项b，就要先给数据集X增加全为1的一列，这样才会把b包含在W中；如果不添加，那么模型是强制过原点的。

以上便是线性回归模型中参数估计的推导过程。

三、标准线性回归

1.对于对给定数据集X和对应目标值y，线性回归目的是要找到回归系数w，使用线性方程来拟合这些数据点。
2.标准线性回归：

• 通常求取回归系数的做法是，求得使平方误差最下的w
• 平方误差

• 解出回归系数

注：直接用此公式时需注意矩阵的求逆，需要判断矩阵行列式不为零，否则不能直接求逆。

#!/usr/bin/env python 
# -*- coding:utf-8 -*-
# numpy函数库中的所有模块引入当前的命名空间
# 后者不建议使用，如果下次引用和numpy里的函数一样的情况，就会出现命名冲突。
from numpy import *
import matplotlib.pyplot as plt

# 该函数是用来打开一个用tab键分割的文本文件，默认文件每行的最后一个值是目标值

def loadDataSet(fileName):  
    # 读出每行有n个数据，将n-1作为特征数,如果传入的txt文件是三列的，则numFeat = 2
    numFeat = len(open(fileName).readline().split('\t')) - 1    
    dataMat = []    
    labelMat = []   
    # 打开文件
    fr = open(fileName)  
    # readlines() 读取一行的数据
    for line in fr.readlines():  
        # 定义一个列表，来存取每一行的数据
        lineArr = [] 
        # 每行的数据根据tab键来划分，存到列表中
        curLine = line.strip().split('\t')  
        # float()不能将整个list中的元素进行类型转换，所以用一个循环，一个元素一个元素地转换
        for i in range(numFeat):
            # 将n-1个特征组成一个新list，强制类型转换成float
            lineArr.append(float(curLine[i]))   
        # 形成双层list形成一个矩阵
        dataMat.append(lineArr)
        # 将最后一个数值作为目标值
        labelMat.append(float(curLine[-1]))
    return dataMat, labelMat

# 计算最佳拟合直线
# 标准的线性回归函数，使用最小二乘法
def standRegres(yArr, xArr):
    # 首先读入x和y并将它们保存到矩阵中
    xMat = mat(xArr)
    # 和transpose()一个意思
    yMat = mat(yArr).T
    # 计算x矩阵和x矩阵的转置乘积
    xTx = xMat.T * xMat
    # 使用的numpy中的linalg库，来计算行列式
    # 计算系数向量w的最佳估计，其中要求xTx的逆，所以先要判断它是否为满秩矩阵（行列式不为0），
    if linalg.det(xTx) == 0.0:
        print("This matrix is singular, cannot do inverse222")
        return
    # 回归系数
    ws = xTx.I * (xMat.T * yMat)
    return ws, xMat, yMat

if __name__ == '__main__':
	xArr, yArr = loadDataSet('ex0.txt')
	ws, xMat, yMat= standRegres(yArr, xArr)
	yHat = xMat * ws
	
	# 替换ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0])
	# 将xArr中第二列的数据添加进来，数组下标+1等于数组列数
	for i in range(len(xArr)):
	    xcord.append(xArr[i][1])
	    
	# 对象，可以想象为一张画布；
	fig = plt.figure()   
	# add_subplot中参数111代表，一行一列，图像画在从左到右从上到下的第9块    
	ax = fig.add_subplot(111)  
	# 将数据添加到画布上
	ax.scatter(xcord,yArr)  
	
	xCopy = xMat.copy()
	# 先将矩阵进行排序
	xCopy.sort(0)
	yHat = xCopy * ws
	
	ax.plot(xCopy[: ,1], yHat, 'red')  # 画出拟合出的直线
	plt.show()

标准线性回归的图像如下所示：

四、局部加权线性回归（LWLR）

线性回归的缺点是容易出现欠拟合，采用局部加权线性回归，给与每一个待预测点附近的点一定的权重，在该子集上基于最小平方误差进行回归。这种算法每次预测前需要先选出相应数据子集。对应回归系数的解为：

其中W是一个矩阵，用来给每一个数据点赋予权重。类似于SVM中的核，常用的核是高斯核，介绍见下图（见《机器学习实战》P142）。

#!/usr/bin/env python
# -*- coding:utf-8 -*-
from numpy import *
import matplotlib.pyplot as plt

# 局部加权线性回归，返回该条样本预测值
def lwlr(testPoint, xArr, yArr, k=1.0):
    xMat = mat(xArr)
    yMat = mat(yArr).T
    m = shape(xMat)[0]
 # 创建为单位矩阵，再mat转换数据格式     因为后面是与原数据矩阵运算，所以这里是为了后面运算且不带来其他影响
    weights = mat(eye((m))) 
     # 利用高斯公式创建权重W     遍历所有数据，给它们一个权重
    for j in range(m):      
        # 高斯核公式1
        diffMat = testPoint - xMat[j,:]  
        # 高斯核公式2    矩阵*矩阵.T 转行向量为一个值    权重值以指数级衰减
        weights[j, j] = exp(diffMat * diffMat.T / (-2.0 * k ** 2))
    # 求回归系数公式1
    xTx = xMat.T * (weights * xMat) 
    # 判断是否有逆矩阵
    if (linalg).det(xTx) == 0.0: 
        print("This matrix is singulat, cannot do inverse1111")
        return
    # 求回归系数公式2
    ws = xTx.I * (xMat.T * (weights * yMat))  
    return testPoint * ws


# 循环所有点求出所有的预测值
def lwlrTest(testArr, xArr, yArr, k=1.0):
    # 传入的k值决定了样本的权重，1和原来一样一条直线，0.01拟合程度不错，0.003纳入太多噪声点过拟合了
    m = shape(testArr)[0]
    yHat = zeros(m)
    
    # 返回该条样本的预测目标值
    for i in range(m):  
        yHat[i] = lwlr(testArr[i], xArr, yArr, k)
    return yHat
if __name__ == '__main__':
	from linearRegression import regression
	xArr, yArr = regression.loadDataSet('ex0.txt')
	# 求所有预测值
	yHat = lwlrTest(xArr, xArr, yArr, 0.01)
	# 绘制数据点和拟合线（局部加权线性回归）
	xMat = mat(xArr)
	# 画拟合线 需要获得所有横坐标从小到大的坐标
	srtInd = xMat[:,1].argsort(0)  
	# 获得排序后的数据
	xSort = xMat[srtInd][:,0,:] 
	
	fig = plt.figure()
	ax = fig.add_subplot(111)
	ax.plot(xSort[:,1],yHat[srtInd],color = 'red')
	ax.scatter(xMat[:,1].flatten().A[0],mat(yArr).T.flatten().A[0])
	plt.show()

yHat = lwlrTest(xArr, xArr, yArr, 0.003)

根据权重选择不同，可以得到下面三种不同的情况

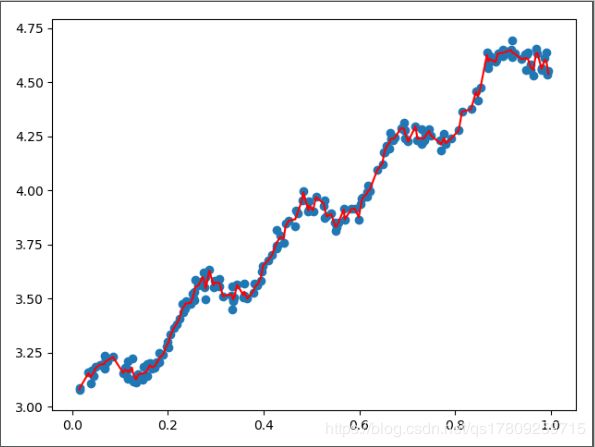
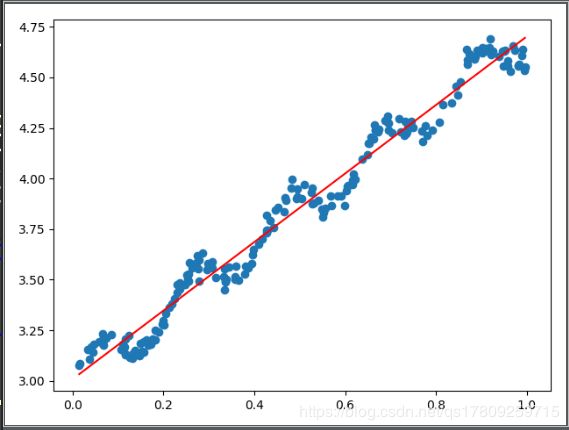
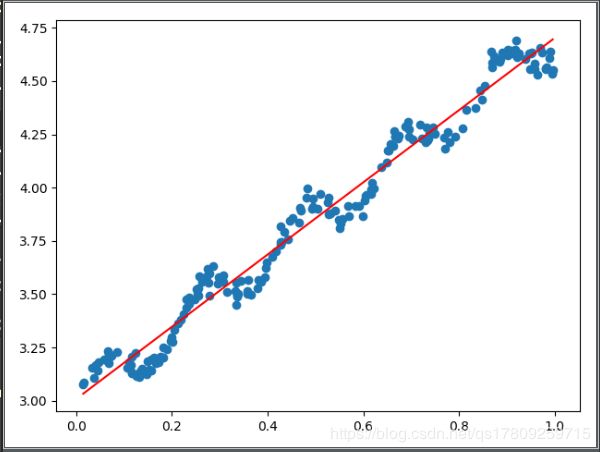
上图中的k=1，中图k=0.01，下图k=0.003，可以看到图一依然是欠拟合的；图二模型已经能够很好地表达原始数据的变化趋势和潜在规律；而图三已经把噪声点考虑在内了，造成了一定程度上过拟合。

五、总结

对于局部加权线性回归总结一下步骤:

• step1：对于需要查询的输入x，找到其领域的训练样本
• step2：对于领域的训练集赋予更大的权重，求取回归系数w使得

• 最小，其中W(i)为权重值
• step3：预测输出：wx
• step4：对于新的输入，重复1-3

从步骤中可以看出，这个算法是一个非参数学习算法（ non-parametric learning algorithm），非参数学习算法每次预测值的时候都要重新训练数据得到新的参数值才能计算预测输出。算法所需要的计算量根据需要查询的输入的数量呈线性增加。

与之对应地，标准线性回归是一种参数学习算法（parametric learning algorithm）， 有固定的（指的是：值的大小是固定）、有限的参数，通过训练样本，找到合适的参数后，对于之后未知的输入，我们可以直接利用这组参数得出其相应的预测输出。

上面的推导和代码实现中的LWLR还存在一个很明显的问题，每次对数据集重新训练都要使用整个数据集。而事实上，随着K的变小，远离查询点的数据的权重趋近于0。如果可以避免这些重复且对结果没有影响的计算将会大大减少计算量。所以这里可以像KNN一样只考虑领域中有限的N个训练点，实现真正的“局部”，那么误差准则可以变为：

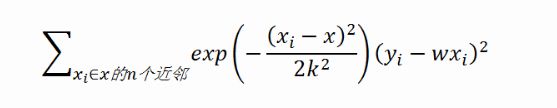
六、示例：预测鲍鱼的年龄

# -*- coding:utf-8 -*-
import numpy as np


def loadDataSet(fileName):
    numFeat = len(open(fileName).readline().split('\t')) - 1
    xArr = []
    yArr = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        xArr.append(lineArr)
        yArr.append(float(curLine[-1]))
    return xArr, yArr


def lwlr(testPoint, xArr, yArr, k=1.0):
    xMat = np.mat(xArr);
    yMat = np.mat(yArr).T
    m = np.shape(xMat)[0]
    # 创建权重对角矩阵
    weights = np.mat(np.eye((m)))  
    # 遍历数据集计算每个样本的权重
    for j in range(m):  
        diffMat = testPoint - xMat[j, :]
        weights[j, j] = np.exp(diffMat * diffMat.T / (-2.0 * k ** 2))
    xTx = xMat.T * (weights * xMat)
    if np.linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵,不能求逆")
        return
    # 计算回归系数
    ws = xTx.I * (xMat.T * (weights * yMat))  
    return testPoint * ws


def lwlrTest(testArr, xArr, yArr, k=1.0):
	# 计算测试数据集大小
    m = np.shape(testArr)[0]  
    yHat = np.zeros(m)
    # 对每个样本点进行预测
    for i in range(m):  
        yHat[i] = lwlr(testArr[i], xArr, yArr, k)
    return yHat


def standRegres(xArr, yArr):
    xMat = np.mat(xArr);
    yMat = np.mat(yArr).T
     # 根据文中推导的公示计算回归系数
    xTx = xMat.T * xMat 
    if np.linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵,不能求逆")
        return
    ws = xTx.I * (xMat.T * yMat)
    return ws


def rssError(yArr, yHatArr):
    return ((yArr - yHatArr) ** 2).sum()


if __name__ == '__main__':
    abX, abY = loadDataSet('abalone.txt')
    print('训练集与测试集相同:局部加权线性回归,核k的大小对预测的影响:')
    yHat01 = lwlrTest(abX[0:99], abX[0:99], abY[0:99], 0.1)
    yHat1 = lwlrTest(abX[0:99], abX[0:99], abY[0:99], 1)
    yHat10 = lwlrTest(abX[0:99], abX[0:99], abY[0:99], 10)
    print('k=0.1时,误差大小为:', rssError(abY[0:99], yHat01.T))
    print('k=1  时,误差大小为:', rssError(abY[0:99], yHat1.T))
    print('k=10 时,误差大小为:', rssError(abY[0:99], yHat10.T))

    print('')

    print('训练集与测试集不同:局部加权线性回归,核k的大小是越小越好吗？更换数据集,测试结果如下:')
    yHat01 = lwlrTest(abX[100:199], abX[0:99], abY[0:99], 0.1)
    yHat1 = lwlrTest(abX[100:199], abX[0:99], abY[0:99], 1)
    yHat10 = lwlrTest(abX[100:199], abX[0:99], abY[0:99], 10)
    print('k=0.1时,误差大小为:', rssError(abY[100:199], yHat01.T))
    print('k=1  时,误差大小为:', rssError(abY[100:199], yHat1.T))
    print('k=10 时,误差大小为:', rssError(abY[100:199], yHat10.T))

    print('')

    print('训练集与测试集不同:简单的线性归回与k=1时的局部加权线性回归对比:')
    print('k=1时,误差大小为:', rssError(abY[100:199], yHat1.T))
    ws = standRegres(abX[0:99], abY[0:99])
    yHat = np.mat(abX[100:199]) * ws
    print('简单的线性回归误差大小:', rssError(abY[100:199], yHat.T.A))

参考：
《机器学习实战》

https://www.cnblogs.com/mooba/p/5947161.html?utm_source=itdadao&utm_medium=referral

https://zhuanlan.zhihu.com/p/55094412?utm_source=qq&utm_medium=social&utm_oi=1091452863145926656