[从零手写VIO|第二节]从已有轨迹生成imu数据推导

论文在这儿

思路1指路——从零手写VIO|第二节——imu.cpp代码解析
思路2参考资料

摘要

本文介绍了一种通用的视惯性同步定位、映射和标定的连续时间框架。我们展示了如何使用Spline参数化，以密切匹配传感器的扭矩最小运动。与传统的离散时间方法相比，连续时间方法特别适用于解决高帧速率传感器和多个非同步设备的问题。通过建立多个非同步器件的相对位姿和内部参数，验证了该方法在多传感器视觉惯性SLAM和标定中的适用性。我们也通过评估和统一处理的全局滚动快门相机在视觉和视觉惯性SLAM系统展示了该方法的优点。

1. 描述了一种使用廉价的传感器CMOS相机和MEMS IMU来实现SLAM的方法。我们利用一个连续时间模型来模拟相机的轨迹，这自然使我们能够融合来自许多不同步的、潜在的高速率传感器的信息，同时限制状态大小。我们明确地对相机的滚动快门进行建模(图1)，并在惯性测量中产生误差。该模型不局限于视觉惯性SLAM，还可以简化其他传感器的集成，如旋转SICK激光雷达。

2. 该方法的另一个重要应用是不同步的多传感器内部和外部最小二乘校正。通过定义连续时间模型中所有传感器的姿态，可以联合估计所有传感器的参数，包括测量时间导数的传感器，如陀螺仪和加速度计。给定近似的初始传感器配置，我们可以找到非常精确的传感器参数。

1. 连续时间的表示

1.1 相机位姿变换

我们用表示帧间齐次点变换的4*4矩阵来表示摄像机之间的变换。例如，$T_{b,a}$表示将坐标系a中定义的齐次点变换为坐标系b中等价点的矩阵，我们可以分解$T_{b,a}$如下:

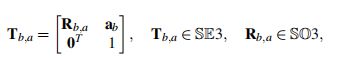
如果$T_{b,a}$表示在时间$∆t$秒内，在帧$T_{w,a}$与帧$T_{w,b}$(其中w为世界坐标系)之间以恒定的角速度和线速度运动，该速度可表示为矩阵形式为:

其中log是矩阵对数。对于矩阵组SE3，对数映射和它的逆(指数映射)可以以封闭的形式计算.

1.2 C2-continuous curves in SE3

我们的方法的核心是一个连续的轨迹表示。我们选择了这样一个公式:
1） 允许系统在线和批量运行
2） 系统具有C2的连续性，使我们能够预测IMU的测量值
3） 具有一个很好的近似最小扭矩轨迹
4） 是可参数化且无奇异点的刚体运动

Cubic B-Splines是R3中众所周知的轨迹表示法，但在处理3D旋转(如SO3中的插值)时却不那么容易应用。例如，C2的连续性不一定保留。我们选择使用使用Lie代数形成的累积基函数来参数化一个连续的轨迹。利用累积B-Splines基函数首次提出了四元数插值。这个表达式不仅是C2连续的，而且它还提供了一个非常简单的二阶导数公式。

1.2.1 Representing B-Splines with cumulative basis functions

B-Splines曲线的标准基函数表示为：

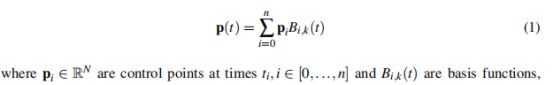
将式(1)重新组织成累积形式为：


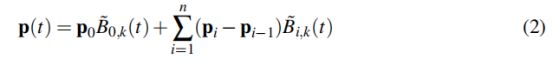
写成矩阵形式：

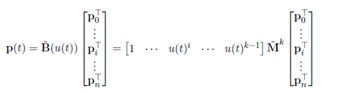
其中，


我们可以重写方程2来描述SE3中的轨迹（指数对数映射之后得到）：

假设控制点个数k=4,插值点在$[t_i,t_{i+1}]$区间，则其样条值与$t_{i-1},t_i,t_{i+1},t_{i+2}$的基函数和控制点有关，得到：

展开得到：

其中$B(u(t))$表达如下：

最终得到SE(3)下三次累积B-样条的公式变成了如下形式：

基于以上B-样条公式可以对IMU数据进行插值，推导过程如下：

首先IMU误差模型表达如下：

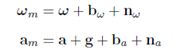
用B-样条方法可以得到连续时间下的陀螺仪角速率和加表的加速度值，重新表达以上公式，如下：

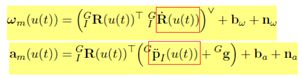
其中R,P为矩阵T的子集，要求出R的一介导和P的二阶导，需要先求出T矩阵的一阶、二阶导。将矩阵T表示公式简化如下：

其中对T矩阵求一阶、二阶偏导如下。

基于前面的求解可以得到，累积基的矩阵表示B和对时间的积分：

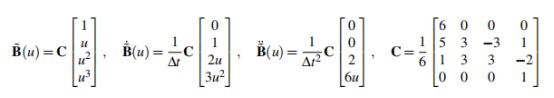
（7）
Spline轨迹中的位姿现在定义为:

所以，我们可以将姿态对时间的一阶导数和二阶导数表示为:

这里以A0计算推导为例，A1，A2推导步骤类似，这里就只推导A0：

首先对A0泰勒展开：

求一阶导如下：

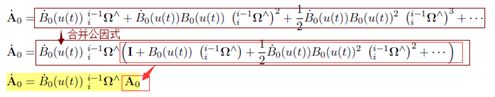
求二阶导如下：

B0以及它的一阶、二阶导数见之前的式（7），整理得：



同样基于以上步骤可以推导出A1,A2以及它们的一阶二阶导数。

将这个过程反推上去，就可以计算出连续时间下imu的角速率和加速度信息。