OpenFoam导入gmesh二维网格
http://openfoamwiki.net/index.php/2D_Mesh_Tutorial_using_GMSH
以下所有翻译自上链接,穿插一点自己的浅薄理解
OpenFoam版本2.3.0 gmesh版本4.1.0
(OpenFoam师兄祖传代码比较老,没空升级,先试着再说。)
创建本教程是为了说明如何使用GMSH开源网格生成器为OpenFOAM生成2D网格。 默认情况下,OpenFOAM仅适用于3D网格元素,因此需要应用一些特殊步骤来创建2D网格。 这并不是GMSH或OpenFOAM的教程,只是让两个工具协同工作的一些有用步骤。 请注意,显示了两种几何生成方法。 一个使用GMSH GUI来创建几何体,并需要对生成的几何体(.geo)文件进行一些修改。 另一个直接创建几何文件。 网格化可以在两种方式中使用或不使用GUI来完成。
1.在Gmesh中定义好几何和网格
1.1图形用户界面(GUI)和* .geo-modification1.打开GMSH并创建一个新文件。
2.在单个平面(2D)中,首先创建所有点,然后将这些点组合成线,然后将线组合成曲面,从而创建几何体。这些都可以通过Elementary entity-> Add-> New下的Geometry Menu完成。
3.通过选择Geometry菜单下的Elementary entities-> Extrude-> Translate,将最终曲面拉伸为3D。选择“曲面”,然后在查看器中单击曲面。这将把表面扩展到3D空间。扩展的距离和方向在“翻译”选项卡下显示的“上下文几何定义”窗口下定义。
4.现在形状是3D,可以定义边界。要定义边界,请从“Geometry”转到Physical Groups->Add->Surface,然后添加将成为边界的每个曲面。记住边界的顺序,因为GMSH GUI将用数字标记它们,以后需要将其更改为OpenFOAM的文本名称。例如,如果形状是正方形,请选择底部,左侧,顶部,右侧,前面和后面,并将它们分别添加为物理组(如果边界由多个面组成,则可以一起选择它们然后添加物理组)。稍后,名称将从数字更改为“底部”,“左侧”,“顶部”等......这些名称将在OpenFOAM中使用。
5.还必须命名几何体的体。从Geometry中选择Physical Groups-> Add-> Volume并选择体。
6.几何应自动保存为.geo文件,但如果没有,请立即保存。然后在文本编辑器中打开.geo文件。将Physical Surfaces重命名为将在OpenFOAM中使用的名称作为边界名称。您还可以将内部曲面指定给物理曲面,以在几何体中创建内部墙。例如(数字可能不同):
Physical Surface("front") = {28};
Physical Surface("back") = {6};
Physical Surface("bottom") = {27};
Physical Surface("left") = {15};
Physical Surface("top") = {19};
Physical Surface("right") = {23};对于体应该同样处理:
Physical Volume("internal") = {1};7.在.geo文件中,必须修改Extrude语句来使得网格是单层的,然后应reconbined。 通过将Layers{1}和Recombine命令添加到Extrude命令来执行此操作。 这确保了网格块仅在2D中创建,然后扩展到3D,而不是在第3轴中划分。 例如:
Extrude {0, 0, 10} {
Surface{6};
Layers{1};
Recombine;
}8.将.geo文件保存在文本编辑器中,然后使用Geometry菜单下的Reload在GMSH中重新加载。 GMSH不应产生任何错误。
下面是一个简单方形的2D网格.geo文件的示例:
Point(1) = {-100, 100, 0, 1e+22};
Point(2) = {100, 100, 0, 1e+22};
Point(3) = {100, -100, 0, 1e+22};
Point(4) = {-100, -100, 0, 1e+22};
Line(1) = {1, 2};
Line(2) = {2, 3};
Line(3) = {3, 4};
Line(4) = {4, 1};
Line Loop(6) = {4, 1, 2, 3};
Plane Surface(6) = {6};
Physical Volume("internal") = {1};
Extrude {0, 0, 10} {
Surface{6};
Layers{1};
Recombine;
}
Physical Surface("front") = {28};
Physical Surface("back") = {6};
Physical Surface("bottom") = {27};
Physical Surface("left") = {15};
Physical Surface("top") = {19};
Physical Surface("right") = {23};9.通过从“网格”菜单中选择3D,在GMSH中创建网格。 您也可以从命令行执行此操作:gmsh -3
可以通过在Options窗口中的Mesh下设置Element Size Factor来控制网格元素的大小(从主菜单中选择Tools->Options)。 数字越小,网格尺寸越小。 要进行单元大小因子的更改,只需返回Geometry,Reload,然后返回Mesh并单击3D。
10.通过从Mesh菜单中选择“保存”来保存网格。 这将使用与.geo文件相同的名称创建一个文件,但以.msh结尾。 这将由OpenFOAM附带的OpenFOAM实用程序gmshToFoam使用。
1.2从头开始创建* .geo
您也可以在任何编辑器中从头开始创建* .geo文件,而不是通过GUI创建几何体。(因为gmesh自带后台脚本,你也可以不用用鼠标在GUI界面点点点可以直接通过把脚本写好生成几何图形
1.在您选择的编辑器中,创建一个带.geo文件扩展名的新文件。
2.使用以下语法定义2D几何体。
Point() = {, , , };
Line() = {, };
Line Loop() = {(+/-), (+/-), ...};
Plane Surface() = {}; 请注意,Line Loop功能需要排序输入。 相邻线的末端和起点必须匹配,方向(例如顺时针)必须一致。 线的方向可以用减号反转。
请注意,线环中线条的出现顺序将在挤出后再次使用。
3.拉伸面可使用:
surfaceVector[] = Extrude {, , } {
Surface{};
Layers{1}; // create only one layer of elements in the direction of extrusion
Recombine;}; // recombine triangular mesh to quadrangular mesh layers{1}里的1是指在拉伸方向只拉伸一层;reconmbine是将三角网格变成四边网格
其中surfaceVector[]是一个vector容器
surfaceVector [0] =相对平面的surfaceNumber
surfaceVector [1] = volume Volume的数量
surfaceVector [...] =表面周围表面的数量,与行循环中的顺序相同
4.使用以下语法定义物理以供以后用作边界
Physical Surface("") = {}
Physical Surface("") = surfaceVector[];
Physical Volume("") = surfaceVector[1]; 5.为参数化网格定义变量
squareSide = 200; //m
meshThickness = squareSide / 10;
gridsize = squareSide / 20;6. * .geo文件现在应该与此示例类似
// Inputs
squareSide = 200; //m
meshThickness = squareSide / 10;
gridsize = squareSide / 20;
// All numbering counterclockwise from bottom-left corner
Point(1) = {-squareSide/2, -squareSide/2, 0, gridsize};
Point(2) = {squareSide/2, -squareSide/2, 0, gridsize};
Point(3) = {squareSide/2, squareSide/2, 0, gridsize};
Point(4) = {-squareSide/2, squareSide/2, 0, gridsize};
Line(1) = {1, 2}; // bottom line
Line(2) = {2, 3}; // right line
Line(3) = {3, 4}; // top line
Line(4) = {4, 1}; // left line
Line Loop(5) = {1, 2, 3, 4};
// the order of lines in Line Loop is used again in surfaceVector[]
Plane Surface(6) = {5};
surfaceVector[] = Extrude {0, 0, meshThickness} {
Surface{6};
Layers{1};
Recombine;
};
/* surfaceVector contains in the following order:
[0] - front surface (opposed to source surface)
[1] - extruded volume
[2] - bottom surface (belonging to 1st line in "Line Loop (6)")
[3] - right surface (belonging to 2nd line in "Line Loop (6)")
[4] - top surface (belonging to 3rd line in "Line Loop (6)")
[5] - left surface (belonging to 4th line in "Line Loop (6)") */
Physical Surface("front") = surfaceVector[0];
Physical Volume("internal") = surfaceVector[1];
Physical Surface("bottom") = surfaceVector[2];
Physical Surface("right") = surfaceVector[3];
Physical Surface("top") = surfaceVector[4];
Physical Surface("left") = surfaceVector[5];
Physical Surface("back") = {6}; // from Plane Surface (6) ...
/* On my PC, the file must end with a free line to avoid errors which might come from different control characters in UNIX, Mac and Windows! Just to be save, insert one line below this comment!*/7.使用GUI或命令行对* .geo-File进行网格化,如上一章所示。
1.3可选:结构化网格
有几种方法可以在GMSH中获得结构化网格。 简单几何的一种简单方法是添加:
Transfinite Surface{}={, , ...};
// forces later meshing to contain structured triangles
// e.g. Transfinite Surface{6} = {1,2,3,4};
Recombine Surface{};
//combine triangles to quadrangles
// e.g.Recombine Surface{6}; 就在* .geo文件中的extrusion命令之前。
例如:
// Inputs
squareSide = 200; //m
meshThickness = squareSide / 10;
gridsize = squareSide / 10;
// Geometry
Point(1) = {-squareSide/2, -squareSide/2, 0, gridsize};
Point(2) = {squareSide/2, -squareSide/2, 0, gridsize};
Point(3) = {squareSide/2, squareSide/2, 0, gridsize};
Point(4) = {-squareSide/2, squareSide/2, 0, gridsize};
Line(1) = {1, 2}; // bottom line
Line(2) = {2, 3}; // right line
Line(3) = {3, 4}; // top line
Line(4) = {4, 1}; // left line
Line Loop(5) = {1, 2, 3, 4};
Plane Surface(6) = {5};
//Transfinite surface:
Transfinite Surface {6};
Recombine Surface {6};
surfaceVector[] = Extrude {0, 0, meshThickness} {
Surface{6};
Layers{1};
Recombine;
};
surfaceVector contains in the following order:
[0] - front surface (opposed to source surface)
[1] - extruded volume
[2] - bottom surface (belonging to 1st line in "Line Loop (6)")
[3] - right surface (belonging to 2nd line in "Line Loop (6)")
[4] - top surface (belonging to 3rd line in "Line Loop (6)")
[5] - left surface (belonging to 4th line in "Line Loop (6)")
Physical Surface("front") = surfaceVector[0];
Physical Volume("internal") = surfaceVector[1];
Physical Surface("bottom") = surfaceVector[2];
Physical Surface("right") = surfaceVector[3];
Physical Surface("top") = surfaceVector[4];
Physical Surface("left") = surfaceVector[5];
Physical Surface("back") = {6};2将网格转换为OpenFOAM
1.必须已经创建了一个带有controlDict文件的OpenFOAM案例目录。 将.msh文件复制到案例目录中。
2.打开命令控制台并转到案例目录,然后输入gmshToFoam
gmshToFoam square.msh
这将在constant/ polyMesh目录下创建OpenFOAM使用的网格。 如果有任何错误,请确保设置了正确的案例目录(请参阅OpenFOAM文档,或使用预先发布的案例目录,如icoFoam或simpleFoam)。 如果错误表明不存在3D元素,或者存在其他网格问题,请确保在本教程的GMSH部分中遵循所有步骤。
3.通过从控制台运行checkMesh,检查网格是否符合OpenFOAM标准。
4.要确认boundary是否为OpenFOAM网格,请在constant
/ polyMesh下的case目录中打开边界文件。 每个边界都在这里定义。 对于沿第3维的面,将类型设置为“空”。 您还可以使用Contrib modifyPatches来自动执行该操作。 例如:
back
{
type empty;
nFaces 2858;
startFace 4217;
}
front
{
type empty;
nFaces 2858;
startFace 7075;
}这将向OpenFOAM表明这是2D案例。 确保存在GMSH .geo文件中定义的所有其他边界作为物理表面。 也可能有一个defaultFaces边界应该有nFaces = 0(不清楚如果nFaces不为0会发生什么):
defaultFaces
{
type patch;
nFaces 0;
startFace 10073;
}或者,您可以在shell或shell脚本中使用awk命令编辑constant/ polyMesh / boundary字典。
$ awk -v RS="\0" -v ORS="" '{ gsub(/(patch name 1)\n {\n type patch/, "(patch name 1)\n {\n type (geometric patch type)"); print }' constant/polyMesh/boundary > tmp
$ mv tmp constant/polyMesh/boundary
$ awk -v RS="\0" -v ORS="" '{ gsub(/(patch name 2)\n {\n type patch/, "(patch name 2)\n {\n type (geometric patch type)"); print }' constant/polyMesh/boundary > tmp
$ mv tmp constant/polyMesh/boundary
...
$ awk -v RS="\0" -v ORS="" '{ gsub(/(patch name n)\n {\n type patch/, "(patch name n)\n {\n type (geometric patch type)"); print }' constant/polyMesh/boundary > tmp
$ mv tmp constant/polyMesh/boundary请注意,空格或制表符(\ t符号)的数量对于gsub(输入,输出)很重要,以查找必须更改的内容。 您还可以使用后缀命名所有相同类型的边界(例如surf1_wall,surf2_wall,surf3_empty ......),并且awk将替换找到此模式(例如_wall,_empty,_symmetry ...)的所有部分。
5.要生成internal wall,您需要从“constant / polyMesh / boundary”中删除零大小的patches,并在文件末尾添加两个零大小的patch并命名为internalWallMaster和internalWallSlave。并更新patch的总数(您可以使用 Contrib modifyPatches自动化)然后使用splitMesh在internalWall处剪切网格。 如果您有多个internal wall,请使用splitMeshWithSets。 在导入具有intenalWall的流畅网格时可以找到更多细节。
6.现在,OpenFOAM可以使用2D网格。 确保初始条件文件中的边界名称(例如p,U等等)与边界文件中的边界名称相匹配。 对于empty faces(第三维),在这些文件中将边界类型设置为empty。
7.如果一切顺利,OpenFOAM应该能够将新网格用于2D情况。 如果事情进展不顺利...... OpenFOAM会告诉你。(翻到这里我有点难受。。。
3个网格示例
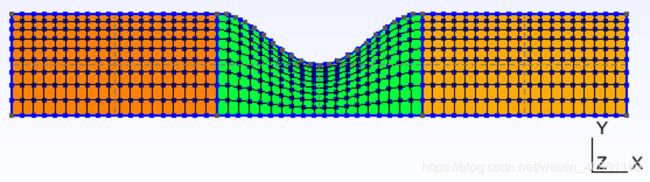
3.1 2D平面对称性狭道
/*
Profile of the axisymmetric stenosis following a cosine
function dependent on the axial coordinate x [1].
f(x) = R * (1 - f0/2 *(1 + Cos(2.0*Pi * (x-x0)/L) )
-- x0 maximum stenosis position.
-- L stenosis length.
-- R vessel radius
-- f0 obstruction fraction, ranging 0--1.
References:
[1] Varghese, S. S., Frankel, S. H., Fischer, P. F., 'Direct numerical simulation of steotic flows. Part 1. Steady flow', Journal of Fluid Mechanics, vol. 582, pp. 253 - 280.
*/
ls = 5;
Xi = 100; // um
Xo = 100; // um
L = 100.0; // um
x0 = Xi + L/2.0;
R = 50.0; // um
f0 = 0.5; // 0--1
Z = 5;
Point(1) = {0, 0, 0, ls};
Point(2) = {Xi, 0, 0, ls};
Point(3) = {Xi, R, 0, ls};
Point(4) = {0, R, 0, ls};
Point(5) = {Xi + L, 0, 0, ls};
Point(6) = {Xi + L + Xo, 0, 0, ls};
Point(7) = {Xi + L + Xo, R, 0, ls};
Point(8) = {Xi + L, R, 0, ls};
Line(1) = {1, 2};
Line(2) = {2, 3};
Line(3) = {3, 4};
Line(4) = {4, 1};
Line(5) = {5, 6};
Line(6) = {6, 7};
Line(7) = {7, 8};
Line(8) = {8, 5};
Line(9) = {2, 5};
pList[0] = 3; // First point label
nPoints = 21; // Number of discretization points (top-right point of the inlet region)
For i In {1 : nPoints}
x = Xi + L*i/(nPoints + 1);
pList[i] = newp;
Point(pList[i]) = {x,
( R * (1 - f0/2 *(1 + Cos(2.0*Pi * (x-x0)/L) ) )),
0,
ls};
EndFor
pList[nPoints+1] = 8; // Last point label (top-left point of the outlet region)
Spline(newl) = pList[];
Transfinite Line {9, 10} = Ceil(L/ls) Using Progression 1;
Transfinite Line {4, -2, 8, -6} = Ceil(R/ls) Using Progression 1.1;
Transfinite Line {1, 3} = Ceil(Xi/ls) Using Progression 1;
Transfinite Line {5, 7} = Ceil(Xo/ls) Using Progression 1;
Line Loop(11) = {4, 1, 2, 3};
Plane Surface(12) = {11};
Line Loop(13) = {2, 10, 8, -9};
Plane Surface(14) = {13};
Line Loop(15) = {8, 5, 6, 7};
Plane Surface(16) = {15};
Transfinite Surface {14,12,16};
Recombine Surface {14,12,16};
Extrude {0,0,Z} {
Surface{14,12,16}; Layers{1}; Recombine;
}
Coherence;
Physical Surface("symmetryLine") = {51, 37, 73};
Physical Surface("frontAndBack") = {60, 38, 82, 16, 14, 12};
Physical Surface("wall") = {59, 29, 81};
Physical Surface("inlet") = {47};
Physical Surface("outlet") = {77};
Physical Volume("volume") = {2, 1, 3};