Qt图形化界面—迷宫最短路径问题

这段时间为了日后的工作需要，遵循霍亚飞老师的《Qt Creator快速入门（第三版）》学了第一大章基础篇的知识，并根据所学的知识尝试性地将之前的迷宫最短路径问题进行了图形化界面的设计。由于本人学艺不精，暂时只能基本实现原函数的基本功能，日后若有时间再慢慢增补吧。

1. 基本介绍

目前这个程序的功能主要有五个：
（1）输入迷宫的尺寸：为便于调试，目前设计的为正方形的迷宫，即长宽尺寸相同。用户只需要输入一个数字，然后按下回车即可完成输入过程。
（2）显示迷宫：我将其快捷键（Ctrl+1）与加速键（Alt+1）均设计为1，这样便于操作，以下的两个键同理。其用于在TextEdit部件中将生成的迷宫，以图形化的界面显示出来。同时，在计算完最短路径后，用于显示迷宫的寻路过程与最短路径。
（3）计算最短路径：通过BFS的方式，在生成的迷宫中查找最短路径，在查找完成后，将其路径数据储存在一个QList容器中，用于之后的使用。
（4）显示最短路径：用于将储存的最短路径以文字的形式表述出来，其中包括沿途的所有节点的坐标，以及其运动方向。
（5）Reset：其对应左上角工具栏的返回按钮，以及菜单栏操作中的一个选项（目前只有这一个选项）。其用于重置当前程序中所有的与迷宫相关的变量，防止旧迷宫的数据对新迷宫的结果造成干扰。
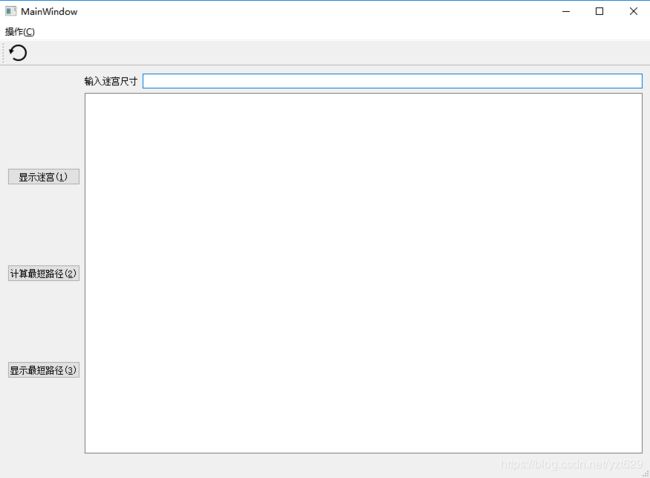
以下为本程序的界面图（可见很简陋，因为我也不知道怎么把它变得好看起来(⊙o⊙)…）

2. 代码实现

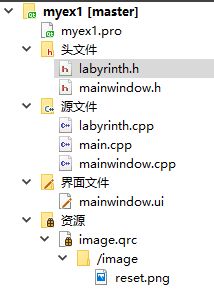
下面是本项目的文件树，其整体构成较为简单，主要是先前的迷宫程序labyrinth.h和labyrinth.cpp，以及本项目的主窗口程序mainwindow.h和mainwindow.cpp，以及自带生成的主程序main.cpp。

2.1 迷宫程序labyrinth

迷宫的实现代码基本上根据上一篇博客修改得来的，为了方便我就直接将所有的声明与定义都放在了头文件里（当然这是不对的，只是因为我太懒而已）。
（1）具体的迷宫实现仍然是借用邓老师的程序，对laby数组进行随机状态分配从而得到迷宫整体，此处由于没有了主函数，所以在随机生成迷宫的开头添加了qsrand函数来根据时间重置随机种子；
（2）最短路径的实现过程仍然是BFS的步步遍历；
（3）最短路径的再现过程仍是通过终点的数据不断反推，不过这次我删除了其中的边推边输出的情况，而是将最短路径储存到了新的shortpath列表中，便于之后的再利用。
同时，我删除了之前的迷宫显示函数，因为这次是需要在ui中直接输出了，为了简便起见，我将输出的过程都转移到了“显示迷宫”的按钮信号槽中（这种方式似乎并不是很棒，但是可以有效地解决问题）。
以下为labyrinth.h文件，labyrinth.cpp文件我嫌麻烦没有将定义转过去。

#ifndef LABYRINTH_H
#define LABYRINTH_H

#include 
#include 
#include 
#include 
#include 
using namespace std;

//这是最小路径的实现函数，通过BFS方式步步遍历的到；如果使用DFS算法，需要穷尽所有的到达终点的路径，最后取最短的

/*迷宫寻径主流的三大算法：广度/深度优先搜素算法，以及A*算法*/
/*相对而言，深度优先搜索是最适合迷宫最短路径寻径的，通过一轮一轮的扁铝，找到的第一条路径也就是最短的路径*/
typedef enum { AVAILABLE, ROUTE, BACKTRACKED, WALL } Status;
typedef enum { UNKNOWN, EAST, SOUTH, WEST, NORTH, NO_WAY } ESWN;
inline ESWN nextESWN(ESWN eswn) { return ESWN(eswn + 1); }
int labySize;  //此处借用dascpp中邓公的随机迷宫生成程序

struct Cell
{
    int x, y = 0;
    Status status = AVAILABLE;  //xy的坐标与类型
    ESWN incoming, outgoing = UNKNOWN;  //进入的方向与出去的方向
    Cell *prev;				  //运行BFS时建立前缀，用于建图形成反推
};

#define LABY_MAX 40
Cell laby[LABY_MAX][LABY_MAX];
int ncheck, nback, length;
Cell* startCell;
Cell* goalCell;

inline Cell *neighbor(Cell *cell) //移动的探测，即得到当前cell的邻居，根据outgoing确定方向
{
    switch (cell->outgoing)
    {
    case EAST:return cell + LABY_MAX;
    case SOUTH:return cell + 1;
    case WEST:return cell - LABY_MAX;
    case NORTH:return cell - 1;
    default:exit(-1); //如果不是这四个方向，即UNKNOWN和NO_WAY，则直接退出这个switch循环
    }
}

inline Cell* advance(Cell* cell)  //实质性的移动，根据cell的incoming移动当前cell到对应的cell
{
    Cell *next;
    switch (cell->outgoing)
    {
    case EAST:next = cell + LABY_MAX; next->incoming = WEST; next->x = cell->x + 1; break;  //这里的操作意思是，现节点的进入为西，即相当于原节点的出是东
    case SOUTH:next = cell + 1;		  next->incoming = NORTH; next->y = cell->y + 1; break;
    case WEST:next = cell - LABY_MAX; next->incoming = EAST; next->x = cell->x - 1; break;
    case NORTH:next = cell - 1;		  next->incoming = SOUTH; next->y = cell->y - 1; break;
    default: exit(-1);
    }
    return next;
}

QList<Cell*> shortestpath;
void inline shortest_path()  //此函数用于根据传递到终点goalCell的数据，来进行路径反推
{
    Cell *c = goalCell;
    c->status = ROUTE;   //所有反推的路径全部将状态改为ROUTE，便于显示路径
    shortestpath.push_front(c);
    while (c->incoming)  //一直反推到最短路径的初始点，即起点，起点的incoming是=0的
    {
        length++;        //length开始循环计数
        auto in = c->incoming;
        c = c->prev;
        switch (in)		 //根据上一个cell的incoming，来反推出当前cell的outgoing，相对取反即可
        {
        case EAST:  c->outgoing = WEST;   break;
        case SOUTH: c->outgoing = NORTH;   break;
        case WEST: c->outgoing = EAST;   break;
        case NORTH: c->outgoing = SOUTH;   break;
        default: exit(-1);
        }
        c->status = ROUTE;
        shortestpath.push_front(c);
    }
    //cout << "shortest path's long is " << length + 1 << endl;  //由于终点是在循环外面做的，所以此处需要加1
}

bool bfs(Cell Laby[LABY_MAX][LABY_MAX], Cell *s, Cell *t)
{
    if ((AVAILABLE != s->status) || (AVAILABLE != t->status)) return false;  //首先，起点和终点必须是能访问的
    deque<Cell*> bfs_path;   //采用BFS算法，所以这里改为使用队列结构
    s->incoming = UNKNOWN; s->status = ROUTE; bfs_path.push_back(s);  //将起点的进入点设为无，然后状态设为在路径上，最后入队列
    do
    {
        Cell *c = bfs_path.front();
        bfs_path.pop_front();
        if (c == t)
        {
            t = c;    //当达到终点时，将此时的c传递给goalCell，因为其中储存了其所有的prev前缀
            return true;
        }
        while (NO_WAY != (c->outgoing = nextESWN(c->outgoing)))   //此处改为遍历当前cell的所有方向一次
        {
            if (AVAILABLE == neighbor(c)->status)  //只要cell的一个方向可以，就将其入队
            {
                Cell* temp = advance(c);
                temp->outgoing = UNKNOWN; temp->status = ROUTE;
                temp->prev = c;					   //每个从当前cell出去的cell，都将原cell设为前缀，由此实现当前图（树）结构的实现
                bfs_path.push_back(temp);
                ncheck++;
            }
        }
        c->status = BACKTRACKED;  //而被bfs过的cell，借用BACKTRACKED状态，表示其已经被扫描过但没有到达终点
    } while (!bfs_path.empty());
    return false;
}

void randLaby(int size)    //根据输入的size生成随机的迷宫
{
    qsrand(QTime(0,0,0).secsTo((QTime::currentTime())));
    labySize = size;  //生成一个输入size的迷宫
    for (int i = 0; i < labySize; i++)
        for (int j = 0; j < labySize; j++)
        {
            laby[i][j].x = i;
            laby[i][j].y = j;
            laby[i][j].incoming =
                laby[i][j].outgoing = UNKNOWN;
            laby[i][j].status = WALL; //边界格点必须是墙
        }
    for (int i = 1; i < labySize - 1; i++)
        for (int j = 1; j < labySize - 1; j++)
            if (rand() % 3) laby[i][j].status = AVAILABLE; //75%的格点为空可用，增加迷宫难度在此酌情修改
    startCell = &laby[rand() % (labySize - 2) + 1][rand() % (labySize - 2) + 1];
    goalCell = &laby[rand() % (labySize - 2) + 1][rand() % (labySize - 2) + 1];
    startCell->status = goalCell->status = AVAILABLE; //起始格点必须可用
}

#endif // LABYRINTH_H

2.2 主窗口程序mainwindow

主窗口程序，主要是在ui中拉出了各个输入框、按钮以及按键等等，在其中主要做的工作是定义各个按钮的信号到槽的链接，并定义了两个私有变量整数size和reset函数，分别用于存储用户输入的size数值，与实现整体的重置工作。
以下为mainwindow.h的代码

#ifndef MAINWINDOW_H
#define MAINWINDOW_H

#include 
#include 

namespace Ui {
class MainWindow;
}

class MainWindow : public QMainWindow
{
    Q_OBJECT

public:
    explicit MainWindow(QWidget *parent = 0);
    ~MainWindow();

private slots:
    void on_lineEdit_returnPressed();

    void on_pushButton_clicked();

    void on_pushButton_2_clicked();

    void on_pushButton_3_clicked();

    void on_actionReset_triggered();

private:
    Ui::MainWindow *ui;
    int size;
    void reset();
};

#endif // MAINWINDOW_H

以下为mainwindow.cpp的代码，其定义了头文件中声明的五个信号槽函数，以及一个重置reset函数。
（1）reset函数：对应迷宫寻路过程中的shortpath最短路径，中心部件TextEdit，以及最短路径长度length，均将其重置。同时对应于迷宫构成数组laby，设置空Cell单元将其全部赋值，从而实现重置过程。
（2）on_pushButton_clicked函数：与按钮1（显示迷宫）点击信号关联的槽函数，其基本沿用了原displaylaby函数的整体类型。但同时也对其做了适当的优化：由于Qt 的TextEdit特殊字符似乎无法显示的问题，我将原函数的显示符号均改成了常规符号，这样导致本次的图形化界面没有之前的好看（我也很无奈。。）；同时将行号与列号具体地显示出来；添加了起点的符号显示，不再只有终点的特殊符号。
（3）on_pushButton_clicked2函数：与按钮2（计算最短路径）点击信号关联的槽函数，其基本沿用了原算法的主函数板块，主要是调用bfs函数计算最短路径后使用shortpath来储存。如果可以计算出最短路径，则在中心部件上打出起点终点以及最短路径的长度。否则说明从起点无法走到终点（即路径都不存在）。
（4）on_pushButton_clicked2函数：与按钮3（显示最短路径）点击信号关联的槽函数。其通过遍历shortpath中存储的每个节点，根据“进入方向-> 节点坐标 -> 离开方向”的形式来输出最短路径上的各个节点。
（5）on_actionReset_triggered函数：其对应的是主界面中的动作Reset，主要就是调用已经定义的reset函数来实现对程序的整体重置。

#include "mainwindow.h"
#include "ui_mainwindow.h"
#include "labyrinth.h"
#include 

MainWindow::MainWindow(QWidget *parent) :
    QMainWindow(parent),
    ui(new Ui::MainWindow)
{
    ui->setupUi(this);
}

MainWindow::~MainWindow()
{
    delete ui;
}

void MainWindow::reset()
{
    ui->textEdit->clear();
    shortestpath.clear();
    length = 0;
    Cell zero;
    startCell = &zero;
    goalCell = &zero;
    for(int i =0; i<LABY_MAX;i++)
        for(int j =0; j<LABY_MAX;j++)
            laby[i][j]=zero;
}

void MainWindow::on_lineEdit_returnPressed()
{
    size = ui->lineEdit->text().toInt();
    randLaby(size);
    ui->textEdit->textCursor().insertText(tr("This laby's size is %1 \n").arg(size));

    //重置最短路径
    shortestpath.clear();
    length = 0;
}

void MainWindow::on_pushButton_clicked()
{
    static char* pattern[5][5] =
    {
        " +", " +", " +", " +", " +",
        " +", "  ", " =", " -", " =",
        " +", " =", "  ", " =", " |",
        " +", " -", " =", "  ", " =",
        " +", " =", " |", " =", "  "
    };
    ui->textEdit->textCursor().insertText("  ");
    for (int j = 0; j < labySize; j++)
        (j < 10) ? ui->textEdit->textCursor().insertText(tr(" %1").arg(j)) : ui->textEdit->textCursor().insertText(tr("%1").arg(j));
    ui->textEdit->textCursor().insertText("\n");
    for (int j = 0; j < labySize; j++)
    {
        (j < 10) ? ui->textEdit->textCursor().insertText(tr(" %1").arg(j)) : ui->textEdit->textCursor().insertText(tr("%1").arg(j));
        for (int i = 0; i < labySize; i++)
        {
            if ((goalCell == &laby[i][j])||(startCell == &laby[i][j]))
            {
                if (goalCell == &laby[i][j])
                    ui->textEdit->textCursor().insertText(" $");
                else
                    ui->textEdit->textCursor().insertText(" #");
            }
            else
                switch (laby[i][j].status)
                {
                case WALL:  ui->textEdit->textCursor().insertText("[]");   break;
                case BACKTRACKED: ui->textEdit->textCursor().insertText("<>");   break;
                case AVAILABLE: ui->textEdit->textCursor().insertText("  ");   break;
                default: ui->textEdit->textCursor().insertText(tr("%1").arg(pattern[laby[i][j].outgoing][laby[i][j].incoming]));  break;
                //老师这里的代码%s后面没有空格，需要加上，不然迷宫会乱掉
                }
        }
        ui->textEdit->textCursor().insertText("\n");
    }
}

void MainWindow::on_pushButton_2_clicked()
{
    if (bfs(laby, startCell, goalCell))  //判断当前迷宫能否从起点走到终点，如果行的话，输出如下
    {
        qDebug() << "true";
        ui->textEdit->textCursor().insertText(tr("This laby's start point is (%1,%2), end point is (%3,%4)\n")
                                              .arg(startCell->x).arg(startCell->y).arg(goalCell->x).arg(goalCell->y));
        shortest_path();//输出当前迷宫从起点到终点的最短路径与长度
        ui->textEdit->textCursor().insertText(tr("The shortest path's distance is %1 \n").arg(length+1));
    }
    else
    {
        qDebug() << "false";
        ui->textEdit->textCursor().insertText(tr("This laby can't go out \n"));
    }
}

void MainWindow::on_pushButton_3_clicked()
{
    foreach (Cell* c, shortestpath)
    {
        ui->textEdit->textCursor().insertText(tr("%1 -> (%2, %3) -> %4 \n")
                                              .arg(c->incoming).arg(c->x).arg(c->y).arg(c->outgoing));
    }
}

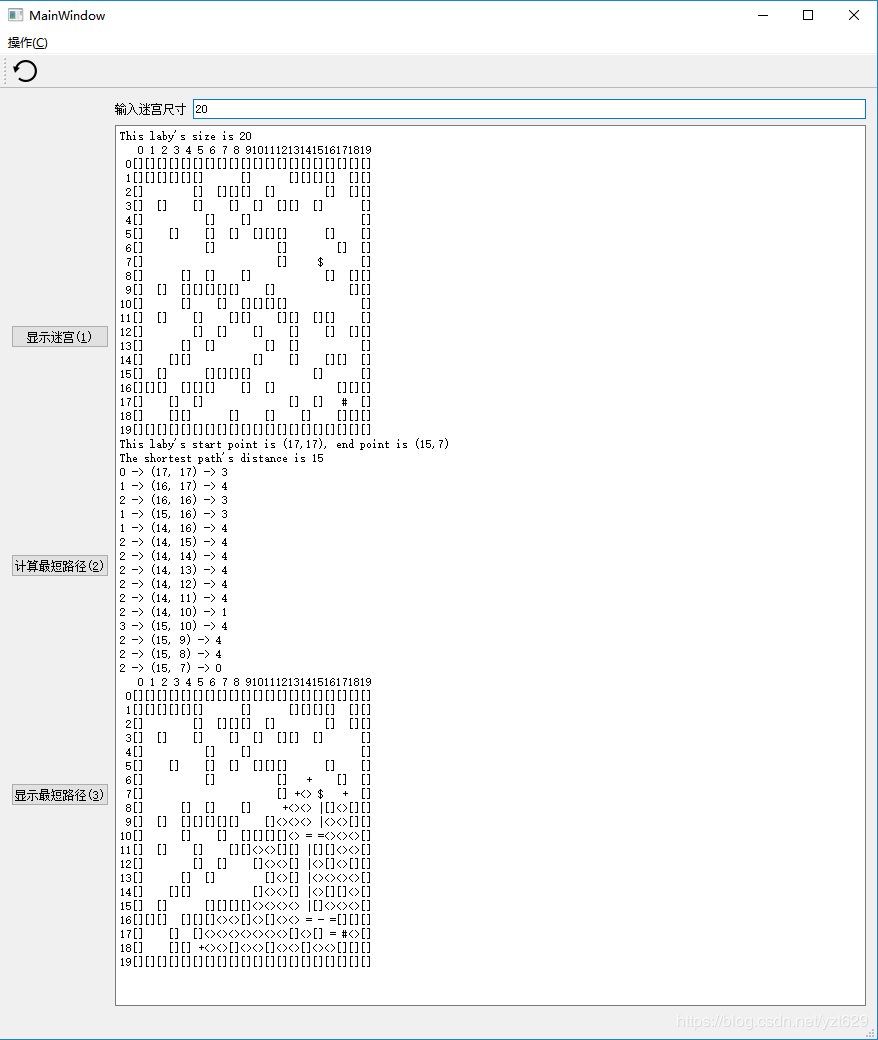
void MainWindow::on_actionReset_triggered()
{
    reset();
}

3. 程序的运行实况

如下图所示为本程序的运行情况，通过“输入尺寸”—“显示迷宫”—“计算最短路径”—“显示最短路径”—“显示迷宫”的操作之后，我们得到的程序界面如图所示。可见其基本实现了原迷宫程序的基本功能，同时根据重置功能与不断更新随机数生成不同的迷宫，实现无数个迷宫的最短路径图形化界面的探寻过程。