动手学习深度学习|卷积神经网络
一 卷积神经网络基础
二维卷积层,常用于处理图像数据。
1 二维互相关运算
二维互相关(cross-correlation)运算的输入是一个二维输入数组和一个二维核(kernel)数组,输出也是一个二维数组,其中核数组通常称为卷积核或过滤器(filter)。卷积核的尺寸通常小于输入数组,卷积核在输入数组上滑动,在每个位置上,卷积核与该位置处的输入子数组按元素相乘并求和,得到输出数组中相应位置的元素
2 二维卷积层
二维卷积层将输入和卷积核做互相关运算,并加上一个标量偏置来得到输出。卷积层的模型参数包括卷积核和标量偏置。
3 互相关运算与卷积运算
卷积层得名于卷积运算,但卷积层中用到的并非卷积运算而是互相关运算。我们将核数组上下翻转、左右翻转,再与输入数组做互相关运算,这一过程就是卷积运算。由于卷积层的核数组是可学习的,所以使用互相关运算与使用卷积运算并无本质区别。
4 特征图与感受野
二维卷积层输出的二维数组可以看作是输入在空间维度(宽和高)上某一级的表征,也叫特征图(feature map)。影响元素 x 的前向计算的所有可能输入区域(可能大于输入的实际尺寸)叫做 x 的感受野(receptive field)。可以通过更深的卷积神经网络使特征图中单个元素的感受野变得更加广阔,从而捕捉输入上更大尺寸的特征。
5 填充和步幅
它们可以对给定形状的输入和卷积核改变输出形状。
填充(padding)是指在输入高和宽的两侧填充元素(通常是0元素),在互相关运算中,卷积核在输入数组上滑动,每次滑动的行数与列数即是步幅(stride)。
6 多输入通道和多输出通道
卷积层的输入和输出可以包含多个通道
7 1x1卷积层
形状为1*1的卷积核,通常称这样的卷积运算为1*1卷积,称包含这种1*1卷积核的卷积层为1*1卷积层.
1*1卷积核可在不改变高宽的情况下,调整通道数。1*1卷积核不识别高和宽维度上相邻元素构成的模式,其主要计算发生在通道维上。假设我们将通道维当作特征维,将高和宽维度上的元素当成数据样本,那么1*1卷积层的作用与全连接层等价。
8 卷积层与全连接层的对比
二维卷积层经常用于处理图像,与此前的全连接层相比,它主要有两个优势:
一是全连接层把图像展平成一个向量,在输入图像上相邻的元素可能因为展平操作不再相邻,网络难以捕捉局部信息。而卷积层的设计,天然地具有提取局部信息的能力。
二是卷积层的参数量更少。
9 池化
二维池化层
池化层主要用于缓解卷积层对位置的过度敏感性。同卷积层一样,池化层每次对输入数据的一个固定形状窗口(又称池化窗口)中的元素计算输出,池化层直接计算池化窗口内元素的最大值或者平均值,该运算也分别叫做最大池化或平均池化。
在处理多通道输入数据时,池化层对每个输入通道分别池化,但不会像卷积层那样将各通道的结果按通道相加。这意味着池化层的输出通道数与输入通道数相等。
二 卷积神经网络进阶
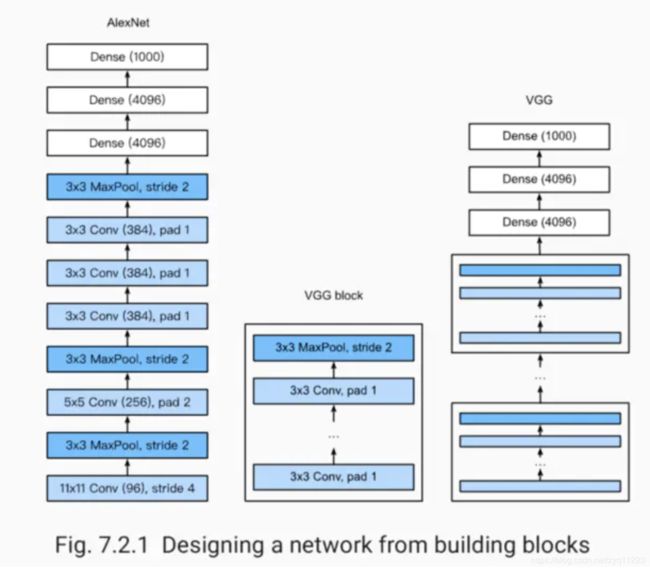
1 深度卷积神经网络(AlexNet)AlexNet
首次证明了学习到的特征可以超越⼿⼯设计的特征,从而⼀举打破计算机视觉研究的前状。
特征:
8层变换,其中有5层卷积和2层全连接隐藏层,以及1个全连接输出层。
将sigmoid激活函数改成了更加简单的ReLU激活函数。
用Dropout来控制全连接层的模型复杂度。
引入数据增强,如翻转、裁剪和颜色变化,从而进一步扩大数据集来缓解过拟合。
2 使用重复元素的网络(VGG)
VGG:通过重复使⽤简单的基础块来构建深度模型。
Block:数个相同的填充为1、窗口形状为3*3
的卷积层,接上一个步幅为2、窗口形状为2*2的最大池化层。
卷积层保持输入的高和宽不变,而池化层则对其减半。
3 ⽹络中的⽹络(NiN)
LeNet、AlexNet和VGG:先以由卷积层构成的模块充分抽取 空间特征,再以由全连接层构成的模块来输出分类结果。
NiN:串联多个由卷积层和“全连接”层构成的小⽹络来构建⼀个深层⽹络。
⽤了输出通道数等于标签类别数的NiN块,然后使⽤全局平均池化层对每个通道中所有元素求平均并直接⽤于分类。
1×1卷积核作用
1.放缩通道数:通过控制卷积核的数量达到通道数的放缩。
2.增加非线性。1×1卷积核的卷积过程相当于全连接层的计算过程,并且还加入了非线性激活函数,从而可以增加网络的非线性。
3.计算参数少
NiN重复使⽤由卷积层和代替全连接层的1×1卷积层构成的NiN块来构建深层⽹络。
NiN去除了容易造成过拟合的全连接输出层,而是将其替换成输出通道数等于标签类别数 的NiN块和全局平均池化层。
NiN的以上设计思想影响了后⾯⼀系列卷积神经⽹络的设计。
4 GoogLeNet
由Inception基础块组成。
Inception块相当于⼀个有4条线路的⼦⽹络。它通过不同窗口形状的卷积层和最⼤池化层来并⾏抽取信息,并使⽤1×1卷积层减少通道数从而降低模型复杂度。
可以⾃定义的超参数是每个层的输出通道数,我们以此来控制模型复杂度。
GoogLeNet模型
完整模型结构