【面试】网易游戏面试题目整理及答案(4)
网易游戏面试题目整理及答案(4)
- 算法部分
算法部分
- 什么是二叉堆?
答:二叉堆本质上是一种完全二叉树,它分为两个类型:最大堆和最小堆。
最大堆:最大堆任何一个父节点的值,都大于等于它左右孩子节点的值。
最小堆:最小堆任何一个父节点的值,都小于等于它左右孩子节点的值。
二叉堆的根节点叫做堆顶。最大堆和最小堆的特点,决定了在最大堆的堆顶是整个堆中的最大元素;最小堆的堆顶是整个堆中最小元素。
问题1:如何构建一个堆呢?
答:这需要依靠二叉堆的自我调整。堆的自我调整过程如下:
对于二叉堆,有几种操作:①插入节点;②删除节点;③构建二叉堆。这几种操作都是基于堆的自我调整。以最小堆为例:
①插入节点
二叉树的节点插入,插入位置是完全二叉树的最后一个位置。比如插入一个新的节点,值是0.

这个时候,让节点0和它的父节点5做比较,如果0小于5,则让新节点“上浮”,和父节点交换位置。
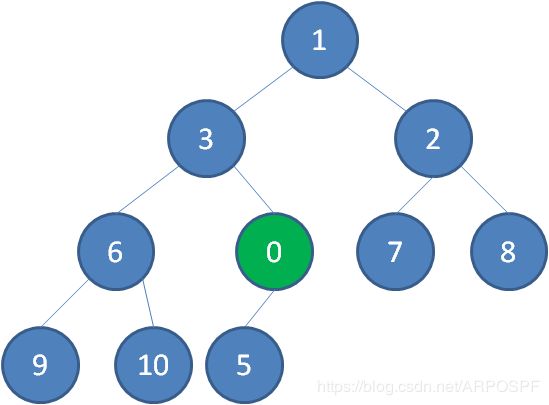
继续用节点0和父节点3做比较,如果0小于3,则让新节点继续“上浮”.
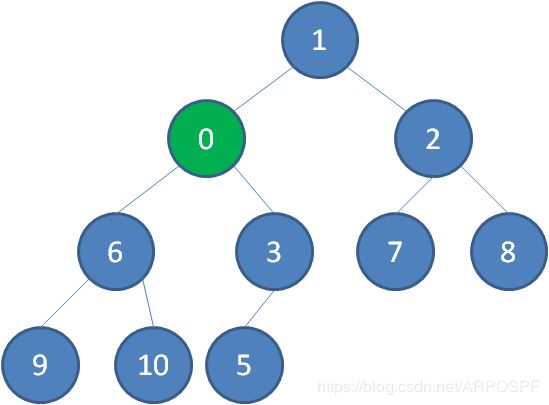
继续比较,最终让新节点0上浮到了堆顶位置。
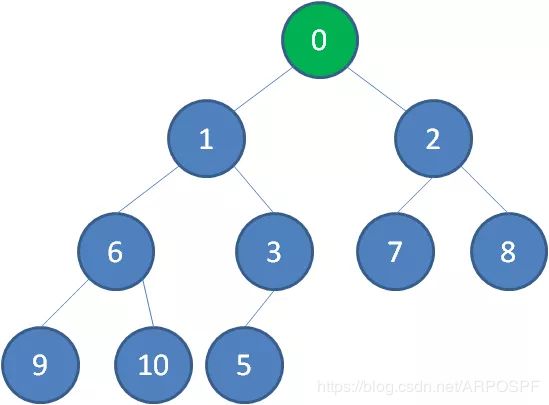
②删除节点
二叉堆的节点删除过程和插入过程正好相反,所删除的是处于堆顶的节点。比如我们删除最小堆的堆顶节点1。

这个时候,为了维持完全二叉树的结构,把堆的最后一个节点10补到原本堆顶的位置。
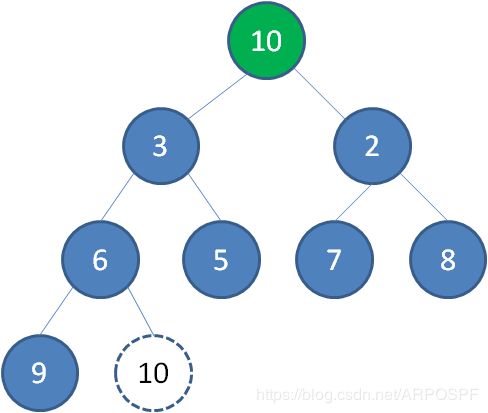
接下来,让移动到堆顶的节点10和它的左右孩子进行比较,如果左右孩子中最小的一个节点(显然是节点2)比节点10小,那么让节点10“下沉”。
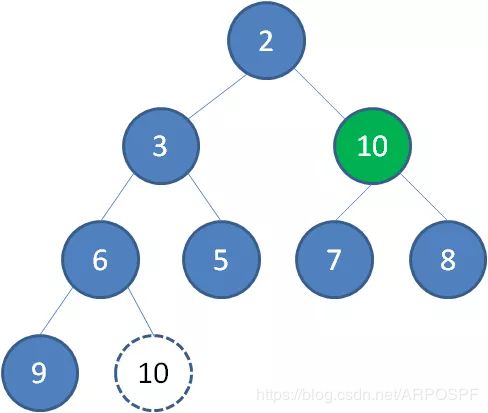
继续让节点10和它的左右孩子做比较,左右孩子中最小的是节点7,由于10大于7,让节点10继续“下沉”.
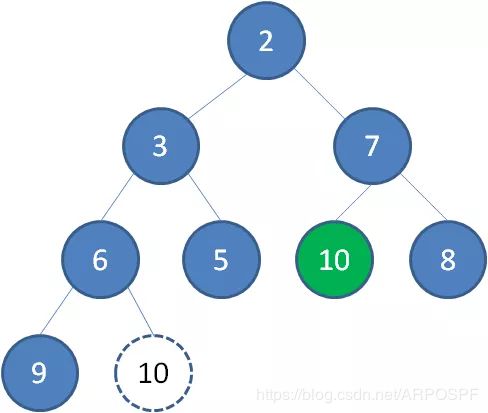
这样一来,二叉堆重新得到了调整。
③构建二叉堆
构建二叉堆,也就是把一个无序的完全二叉树调整为二叉堆,本质上就是让所有非叶子节点依次下沉。例如,如下是一个无序的完全二叉树:
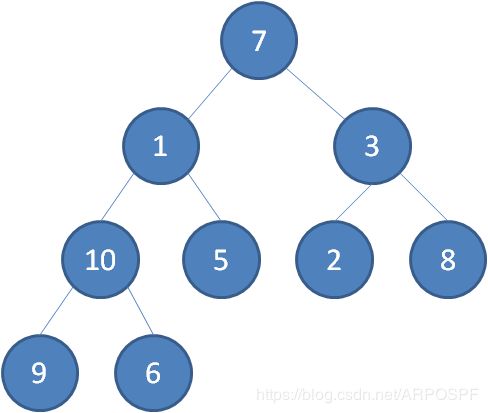
首先从最后一个非叶子节点开始,也就是从节点10开始。如果节点10大于它的左右孩子中最小的一个,则节点10下沉。

接下来,轮到节点3,如果节点3大于它左右孩子中最小的一个,则节点3下沉。
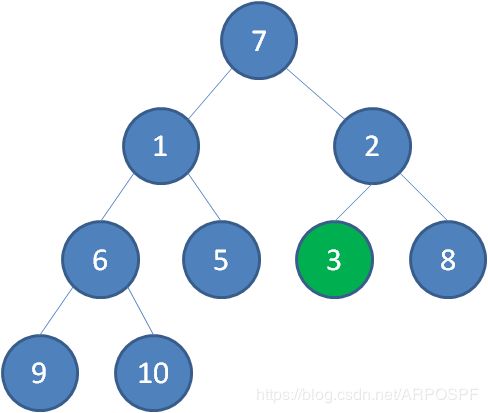
接下来轮到节点1,如果节点1大于它左右孩子中最小的一个,则节点1下沉。事实上节点1小于它的左右孩子,所以不用改变。
接下来轮到节点7,如果节点7大于它左右孩子中最小的一个,则节点7下沉。
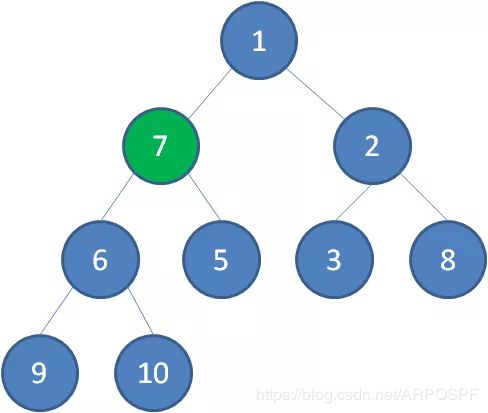
节点7继续比较,继续下沉。
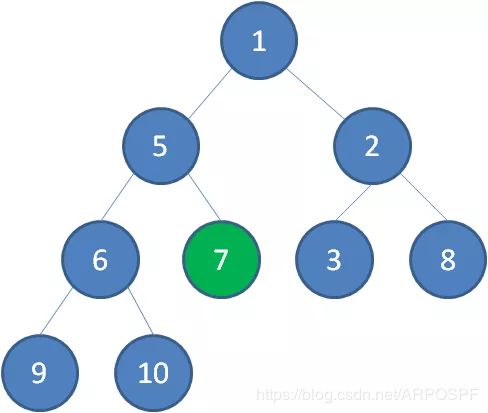
这样一来,一颗无序的完全二叉树就构建成了一个最小堆。
堆的代码实现:
需要明确的是:二叉堆虽然是一颗完全二叉树,但它的存储方式并不是链式存储,而是顺序存储。即二叉堆的所有节点都存储在数组当中。

问题是:在数组中,在没有左右指针的情况下,如何定位到一个父节点的左孩子和右孩子呢?
答:像图中那样,可以依靠数组下标来计算。
假设父节点的下标是parent,那么它的左孩子下标就是2*parent+1;它的右孩子下标就是2*parent+2。
比如上面的例子中,节点6包含9和10两个孩子,节点6在数组中的下标是3,节点9在数组中的下标是7,节点10在数组中的下标是8。
7 = 3 ∗ 2 + 1 7=3*2+1 7=3∗2+1
8 = 3 ∗ 2 + 2 8=3*2+2 8=3∗2+2
刚好符合规律。代码如下:
import java.util.Arrays;
public class HeapOperator {
/**
* 上浮调整
*
* @param array 待调整的堆
*/
public static void upAdjust(int[] array) {
int childIndex = array.length - 1; // 插入的节点一定是左孩子,即lChild=2*parent+1
int parentIndex = (childIndex - 1) / 2;
// temp保存插入的叶子节点值,用于最后的赋值
int temp = array[childIndex];
while (childIndex > 0 && temp < array[parentIndex]) {
//无需真正交换,单向赋值即可
array[childIndex] = array[parentIndex];
childIndex = parentIndex;
parentIndex = (parentIndex - 1) / 2; // ??
}
array[childIndex] = temp;
}
/**
* 下沉调整
*
* @param array 待调整的堆
* @param parentIndex 要下沉的父节点
* @param length 堆的有效大小
*/
public static void downAdjust(int[] array, int parentIndex, int length) {
// temp 保存父节点的值,用于最后的赋值
int temp = array[parentIndex];
int childIndex = 2 * parentIndex + 1;
while (childIndex < length) {
//如果有右孩子,且右孩子小于左孩子的值,则定位到右孩子
if (childIndex + 1 < length && array[childIndex + 1] < array[childIndex]) {
childIndex++;
}
//如果父节点小于任何一个孩子的值,直接跳出
if (temp <= array[childIndex])
break;
//无需真正交换,单向赋值即可
array[parentIndex] = array[childIndex];
parentIndex = childIndex;
childIndex = 2 * parentIndex + 1;
}
array[parentIndex] = temp;
}
/**
* 构建堆
*
* @param array 待调整的堆
*/
public static void buildHeap(int[] array) {
//从最后一个非叶子节点开始,依次下沉调整
for (int i = array.length / 2; i >= 0; i--) {
downAdjust(array, i, array.length - 1);
}
}
public static void main(String[] args) {
int[] array = new int[]{1, 3, 2, 6, 5, 7, 8, 9, 10, 0};
upAdjust(array);
System.out.println(Arrays.toString(array));
array = new int[]{7, 1, 3, 10, 5, 2, 6, 8, 9};
buildHeap(array);
System.out.println(Arrays.toString(array));
}
}
代码中有一个优化的点,就是父节点和孩子节点做连续交换时,并不一定要真的交换,只需要先把交换一方的值存入temp变量,做单向覆盖,循环结束后,再把temp的值存入交换后的最终位置。
二叉堆的用处:是实现堆排序以及优先级队列的基础。
- 什么是堆排序?
答:首先回顾二叉堆和最大堆的特性:①二叉堆本质上是一种完全二叉树;②最大堆的堆顶是整个堆中的最大元素。当我们删除一个最大堆的堆顶(并不是完全删除,而是替换到最后面),经过自我调节,第二大的元素就会被交换上来,成为最大堆的新堆顶。
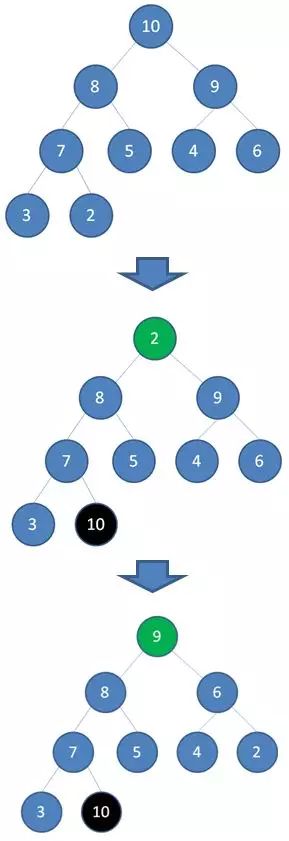
正如上图所示,当我们删除值为10的堆顶节点,经过调整,值为9的新节点就会顶替上来,当我们删除值为9的堆顶节点,经过调节,值为8的新节点就会顶替上来…
由于二叉堆的这个特性,我们每一次删除旧堆顶,调整后的新堆顶都是大小仅次于旧堆顶的节点。那么我们只要反复删除堆顶,反复调节二叉堆,所得到的集合就成为了一个有序集合,过程如下:
1)删除节点9,节点8成为新堆顶:
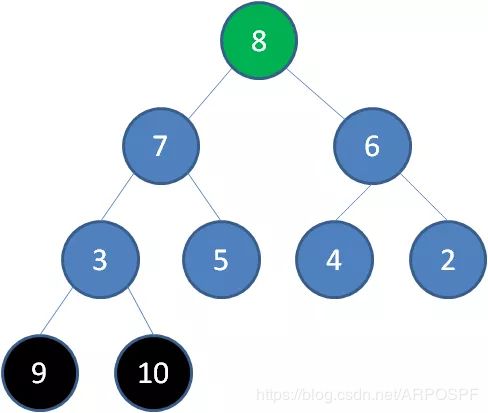
2)删除节点8,节点7成为新堆顶:
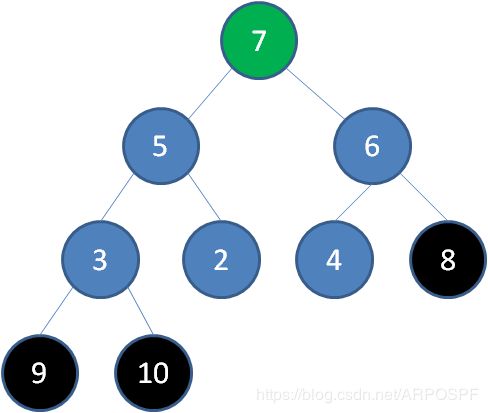
3)删除节点7,节点6成为新堆顶

4)删除节点6,节点5成为新堆顶:
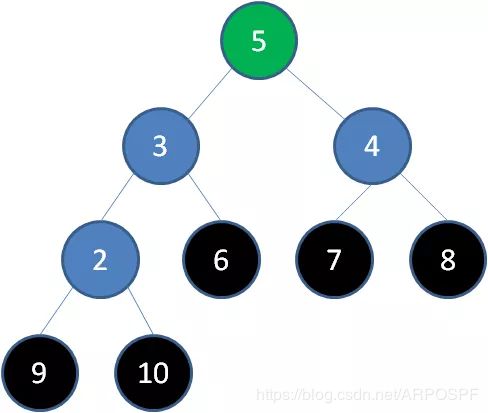
5)删除节点5,节点4成为新堆顶:
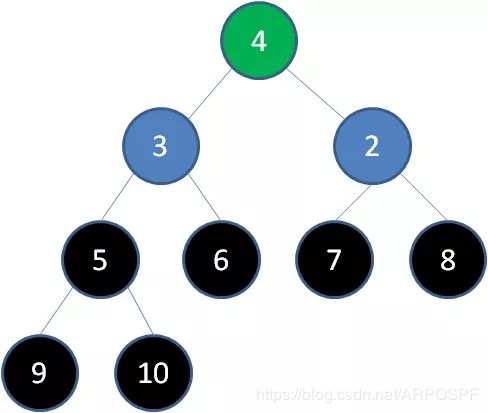
6)删除节点4,节点3成为新堆顶:
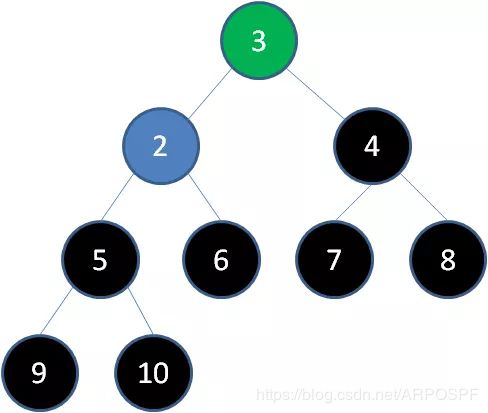
7)删除节点3,节点2成为新堆顶:
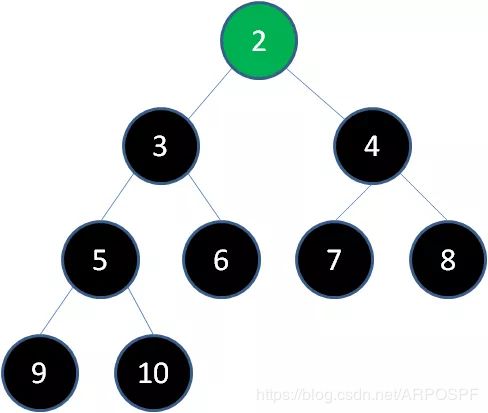
到此为止,我们原本的最大堆已经变成了一个从小到达的有序集合。之前说过二叉堆实际存储再数组当中,数组中的元素排列如下:

由此,可以归纳出堆排序算法的步骤:
①把无序数组构建成二叉堆
②循环删除堆顶元素,移到集合尾部,调节堆产生新的堆顶。
代码如下:
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
int[] arr = new int[]{1, 3, 2, 6, 5, 7, 8, 9, 10, 0};
heapSort(arr);
System.out.println(Arrays.toString(arr));
}
/**
* 堆排序
*
* @param array 待调整的堆
*/
private static void heapSort(int[] array) {
// 1. 把无序数组构建成二叉堆
for (int i = (array.length - 2) / 2; i >= 0; i--) {
downAdjust(array, i, array.length);
}
System.out.println(Arrays.toString(array));
// 2. 循环删除堆顶元素,移到集合尾部,调整堆产生新的堆顶。
for (int i = array.length - 1; i > 0; i--) {
// 最后一个元素和第一个元素交换
int temp = array[i];
array[i] = array[0];
array[0] = temp;
//下沉调整最大堆
downAdjust(array, 0, i);
}
}
/**
* 下沉调整
*
* @param array 待调整的堆
* @param parentIndex 要下沉的父节点
* @param length 堆的有效大小
*/
private static void downAdjust(int[] array, int parentIndex, int length) {
// temp保存父节点值,用于最后的赋值
int temp = array[parentIndex];
int childIndex = 2 * parentIndex + 1;
while (childIndex < length) {
//如果有右孩子,且右孩子大于左孩子的值,则定位到右孩子
if (childIndex + 1 < length && array[childIndex + 1] > array[childIndex]) {
childIndex++;
}
//如果父节点大于任何一个孩子的值,直接跳出
if (temp >= array[childIndex])
break;
//无需真正交换,单向赋值即可
array[parentIndex] = array[childIndex];
parentIndex = childIndex;
childIndex = 2 * childIndex + 1;
}
array[parentIndex] = temp;
}
}
- 求二叉树深度
答:对于一颗二叉树,从根节点到叶节点依次经过的节点(含根、叶节点)行程树的一条路径,最长路径的长度为树的深度。
思路:递归思路,根的高度等于(左子树的高度和右子树的高度中高度较高的那一个高度)+1。
代码如下:
class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
public class TreeDepth {
public int treeDepth(TreeNode root) {
if (root == null) {
return 0;
}
if (root.left == null && root.right == null) {
return 1;
}
//左右子树高度中取较高的那一个高度+1
return treeDepth(root.left) > treeDepth(root.right) ? treeDepth(root.left) + 1 : treeDepth(root.right) + 1;
}
}
- Top k问题
答:对于该问题有四种解题思路:
1)最直接的方法:排序
既然是要前 K 大的数,那么最直接的当然就是排序了,通过如快排等效率较高的排序算法,可以在平均 O(nlogn)的时间复杂度找到结果。这种方式在数据量不大的时候简单可行,但固然不是最优的方法。
2)O(n) 时间复杂度的方法
刚刚提到了快排,熟悉算法题的小伙伴应该知道,快排的 partition 划分思想可以用于计算某个位置的数值等问题,例如用来计算中位数;显然,也适用于计算 TopK 问题
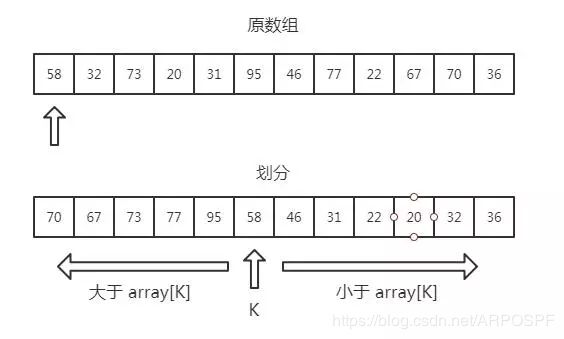
每次经过划分,如果中间值等于K,那么其左边的数就是Top K的数据;当然,如果不等于,只要递归处理左边或者右边的数即可。
该方法的时间复杂度是 O(n) ,简单分析就是第一次划分时遍历数组需要花费 n,而往后每一次都折半(当然不是准确地折半),粗略地计算就是 n + n/2 + n/4 +… < 2n,因此显然时间复杂度是 O(n)。
对比第一个方法显然快了不少,随着数据量的增大,两个方法的时间差距会越来越大
缺点:虽然时间复杂度是 O(n) ,但是缺点也很明显,最主要的就是内存问题,在海量数据的情况下,我们很有可能没办法一次性将数据全部加载入内存,这个时候这个方法就无法完成使命了;还有一点就是这种思路需要我们修改输入的数组,这也是值得考虑的一点。
3)利用分布式思想处理海量数据
面对海量数据,我们就可以放分布式的方向去思考了。我们可以将数据分散在多台机器中,然后每台机器并行计算各自的 TopK 数据,最后汇总,再计算得到最终的 TopK 数据。这种数据分片的分布式思想在面试中非常值得一提,在实际项目中也十分常见。
4)利用最经典的方法,一台机器也能处理海量数据
其实提到 Top K 问题,最经典的解法还是利用堆。维护一个大小为 K 的小顶堆,依次将数据放入堆中,当堆的大小满了的时候,只需要将堆顶元素与下一个数比较:如果大于堆顶元素,则将当前的堆顶元素抛弃,并将该元素插入堆中。遍历完全部数据,Top K 的元素也自然都在堆里面了。

将数据插入堆
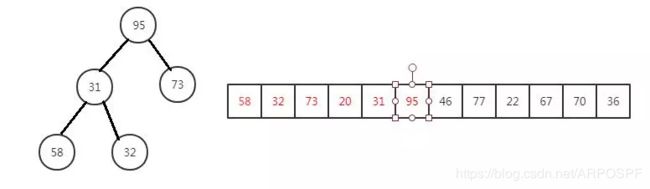
95大于20,进行替换
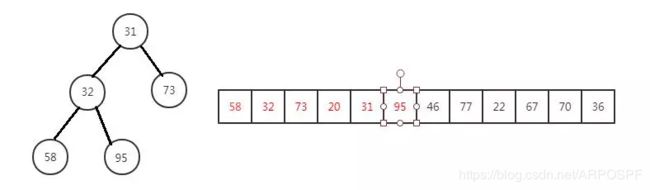
95下沉,维持小顶堆
对于海量数据,我们不需要一次性将全部数据取出来,可以一次只取一部分,因为我们只需要将数据一个个拿来与堆顶比较。
另外还有一个优势就是对于动态数组,我们可以一直都维护一个 K 大小的小顶堆,当有数据被添加到集合中时,我们就直接拿它与堆顶的元素对比。这样,无论任何时候需要查询当前的前 K 大数据,我们都可以里立刻返回给他。
整个操作中,遍历数组需要 O(n) 的时间复杂度,一次堆化操作需要 O(logK),加起来就是 O(nlogK) 的复杂度,换个角度来看,如果 K 远小于 n 的话, O(nlogK) 其实就接近于 O(n) 了,甚至会更快,因此也是十分高效的。
最后,对于 Java,我们可以直接使用优先队列 PriorityQueue 来实现一个小顶堆,这里给个代码:
import java.util.ArrayList;
import java.util.List;
import java.util.PriorityQueue;
import java.util.Queue;
public class TopK {
public static List<Integer> solutionByHeap(int[] input, int k) {
List<Integer> list = new ArrayList<>();
if (k > input.length || k == 0) {
return list;
}
Queue<Integer> queue = new PriorityQueue<>();
for (int num : input) {
if (queue.size() < k) {
queue.add(num);
} else if (queue.peek() < num) {
queue.poll();
queue.add(num);
}
}
while (k-- > 0) {
list.add(queue.poll());
}
return list;
}
}
当然,如果是求前 K 个最小的数,只需要改为大顶堆即可
- 请完成一个函数,输入一颗二叉树,请函数输出它的镜像,如下所示
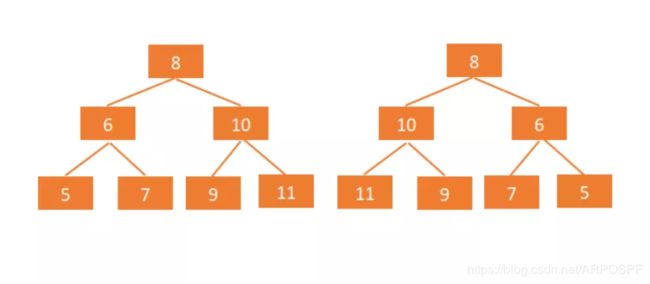
答:求出一个二叉树的镜像,首先要知道什么是二叉树的镜像,通过上图可以得出,镜像就是二叉树的每层节点的左右子树进行相互交换。说白了就是除根节点外,所有的结点中的左子节点的镜像是右子节点,右子节点的镜像变成了左子节点。
因为每个具有非空节点的节点的左右子节点都要进行交换,所以我们可以用递归来解决。
首先,使用递归要找到递归的终止条件,当我们遇到叶子节点的时候,就不用进行递归交换了。所以递归条件就是当前递归的节点是否为空。
if(root==null){
return;
}
然后声明一个临时变量用来存储两个节点交换的值,然后进行左右子树交换。
//进行节点交换
Let tempNode = root.left;
root.left = root.right;
root.right = tempNode;
交换之后,直接递归剩下的节点进行交换就OK。然后返回递归后的树的根节点。
//递归遍历剩余的子节点
insert(root.left)
insert(root.right)
//返回根节点
return root;
完整代码如下:
public class TreeMirror {
public static void mirror(TreeNode root) {
//如果根节点为空,无需处理
if (root == null) {
return;
}
//左子节点和右子节点都为空,无需处理
if (root.left == null && root.right == null) {
return;
}
//左子节点不为空,则对该子节点做镜像处理
if (root.left != null) {
mirror(root.left);
}
//右子节点不为空,则对该子节点做镜像处理
if (root.right != null) {
mirror(root.right);
}
//交换当前节点的左右子节点位置
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
}
}
- 有一个单向链表,如何判断链表有没有环?
答:方法描述如下:
方法1:首先从头节点开始,依次遍历单链表的每一个节点。每遍历到一个新节点,就从头节点重新遍历新节点之前的所有节点,用新节点ID与此节点之前的所有节点ID依次比较。如果发现新节点之前的所有节点当中存在相同节点ID,则说明该节点被遍历过两次,链表有环;如果之前的所有节点当中不存在相同的节点,就继续遍历下一个新节点,继续重复刚才的操作。
例如这样的链表:A->B->C->D->B->C->D, 当遍历到节点D的时候,我们需要比较的是之前的节点A、B、C,不存在相同节点。这时候要遍历的下一个新节点是B,B之前的节点A、B、C、D中恰好也存在B,因此B出现了两次,判断出链表有环。
假设从链表头节点到入环点的距离是D,链表的环长是S。那么算法的时间复杂度是0+1+2+3+…+(D+S-1) = (D+S-1)(D+S)/2 , 可以简单地理解成 **O(NN)**。而此算法没有创建额外存储空间,空间复杂度可以简单地理解成为O(1)。
方法2:首先创建一个以节点ID为键的HashSet集合,用来存储曾经遍历过的节点。然后同样是从头节点开始,依次遍历单链表的每一个节点。每遍历到一个新节点,就用新节点和HashSet集合当中存储的节点作比较,如果发现HashSet当中存在相同节点ID,则说明链表有环;如果HashSet当中不存在相同的节点ID,就把这个新节点的ID存入HashSet,之后进入下一个节点,继续重复刚才的操作。
这个方法在流程上和方法一类似,本质的区别是使用了HashSet作为额外的缓存。
假设从链表头节点到入环点的距离是D,链表的环长是S。而每一次HashSet查找元素的时间复杂度是O(1), 所以总体的时间复杂度是1*(D+S)=D+S,可以简单理解为O(N)。而算法的空间复杂度还是D+S-1,可以简单地理解成O(N)。
方法3:首先创建两个指针1和2(在java里就是两个对象的引用),同时指向这个链表的头节点,然后开始一个大循环,在循环体中,让指针1每次向下移动一个节点,让指针2每次向下移动两个节点,然后比较两个指针指向的节点是否相同,如果相同,则判断出链表有环,如果不同,则继续下一次循环。
例如链表A->B->C->D->B->C->D,两个指针最初都指向节点A,进入第一轮循环,指针1移动到了节点B,指针2移动到了C。第二轮循环,指针1移动到了节点C,指针2移动到了节点B。第三轮循环,指针1移动到了节点D,指针2移动到了节点D,此时两指针指向同一节点,判断出链表有环。
此方法也可以用一个更生动的例子来形容:在一个环形跑道上,两个运动员在同一地点起跑,一个运动员速度快,一个运动员速度慢。当两人跑了一段时间,速度快的运动员必然会从速度慢的运动员身后再次追上并超过,原因很简单,因为跑道是环形的。
假设从链表头节点到入环点的距离是D,链表的环长是S。那么循环会进行S次(为什么是S次,有心的同学可以自己揣摩下),可以简单理解为O(N)。除了两个指针以外,没有使用任何额外存储空间,所以空间复杂度是O(1)。
|--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
补充问题:
问题1:判断两个单向链表是否相交,如果相交,求出交点。
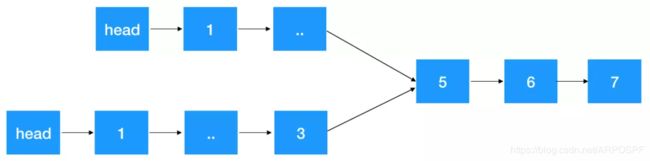
答:注意相交的定义基于节点的引用,而不是基于节点的值。换句话说,如果一个链表的第k个节点与另一个链表的第j个节点是同一节点(引用完全相同),则这两个链表相交。
由于链表本身的性质,如果有一个结点相交,那么相交结点之后的所有结点都是这两个链表共用的,也就是说两个链表的长度主要相差在相交结点之前的结点长度,于是我们有以下思路:
1)如果链表没有长度,则我们先遍历这两个链表拿到两个链表长度,假设分别为L1,L2(L1>=L2),定义p1,p2指针分别指向各自链表head结点,然后p1先往前走L1-L2步。这一步保证了p1,p2指向的指针与相交节点(如果有的话)一样近。
2)然后 p1,p2 不断往后遍历,每次走一步,边遍历边判断相应结点是否相等,如果相等即为这两个链表的相交结点。
问题2:在一个有环链表中,如何找出链表的入环点?
答:继续用快慢指针来解决,如下所示:
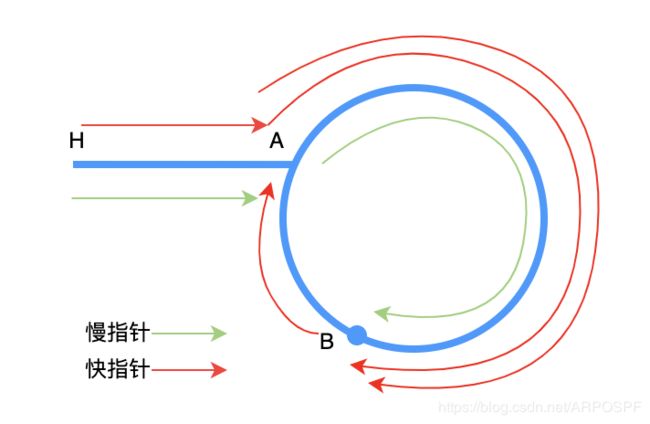
H: 链表头; A: 入环点 ;B: 快慢指针相交点
先做如下约定:
LHA: 链表头H到入环点A的距离;
LAB: 链表节点A顺时针到节点B的距离;
LBA: 链表节点B顺时针到节点A的距离;
根据移动距离,可知:
2慢指针移动距离 = 快指针移动距离,即2(LHA + LAB) = LHA + LAB + LBA + LAB;
最后推导出:LHA = LBA
所以,只要从相交点和头节点同时遍历到的相同节点就能找到入环点.
代码如下:
import java.util.HashSet;
import java.util.Set;
public class CycleListNode {
static class ListNode {
int val;
ListNode next;
public ListNode(int data) {
this.val = data;
}
}
/**
* 快慢指针
*/
public static boolean hasCycleByPoint(ListNode head) {
boolean hasCycle = true;
ListNode fastIndex = head;
ListNode slowIndex = head;
do {
if (fastIndex == null) {
hasCycle = false;
break;
}
if (fastIndex.next == null) {
hasCycle = false;
break;
}
fastIndex = fastIndex.next.next;
slowIndex = slowIndex.next;
} while (fastIndex != slowIndex);
return hasCycle;
}
/**
* hash
*/
public static boolean hasCycleByHash(ListNode head) {
boolean hasCycle = false;
Set set = new HashSet();
while (head != null) {
if (set.contains(head)) {
hasCycle = true;
break;
}
set.add(head);
head = head.next;
}
return hasCycle;
}
/**
* 单链表第一个相交点
* @param head1
* @param head2
* @return
*/
public static ListNode getFirstCommonNode(ListNode head1, ListNode head2) {
int length1 = 0; //链表1的长度
int length2 = 0; //链表2的长度
ListNode p1 = head1;
ListNode p2 = head2;
while (p1.next != null) {
length1++;
p1 = p1.next;
}
while (p2.next != null) {
length2++;
p2 = p2.next;
}
p1 = head1;
p2 = head2;
//p1或p2前进|length1-length2|步
if (length1 >= length2) {
int diffLen = length1 - length2;
while (diffLen > 0) {
p1 = p1.next;
diffLen--;
}
} else {
int diffLen = length2 - length1;
while (diffLen > 0) {
p2 = p2.next;
diffLen--;
}
}
//p1,p2分别往后遍历,边遍历边比较,如果相等,即为第一个相交节点
while (p1 != null && p2.next != null) {
p1 = p1.next;
p2 = p2.next;
if (p1.val == p2.val) {
//p1,p2都为相交节点,返回p1或p2
return p1;
}
}
//如果没有相交节点,返回空指针
return null;
}
/**
* 环形相交点
* F:头结点到入环结点距离
* B:入环结点到快慢指针相交结点距离
* C:快慢指针相交结点到入环结点距离
* 2*慢指针移动距离=快指针移动距离
* 2(F+B)=F+B+B+C
* F = C
*
* @param head
* @return
*/
public static ListNode getEntranceNode(ListNode head) {
ListNode fastIndex = head;
ListNode slowIndex = head;
do {
if (fastIndex == null) {
break;
}
if (fastIndex.next == null) {
fastIndex = fastIndex.next;
break;
}
fastIndex = fastIndex.next.next;
slowIndex = slowIndex.next;
} while (fastIndex != slowIndex);
if (fastIndex == null) {
return null;
}
ListNode headIndex = head;
while (fastIndex != headIndex) {
fastIndex = fastIndex.next;
headIndex = headIndex.next;
}
return fastIndex;
}
public static void main(String[] args) {
test1();
test2();
test3();
}
private static void test1() {
ListNode n1 = new ListNode(1);
ListNode n2 = new ListNode(2);
ListNode n3 = new ListNode(3);
ListNode n4 = new ListNode(4);
ListNode n5 = new ListNode(5);
n1.next = n2;
n2.next = n3;
n3.next = n4;
n4.next = n5;
n5.next = n2;
System.out.println(hasCycleByPoint(n1));
assert getEntranceNode(n1) != null;
System.out.println(getEntranceNode(n1).val);
}
private static void test2() {
ListNode n1 = new ListNode(1);
ListNode n2 = new ListNode(2);
ListNode n3 = new ListNode(3);
ListNode n4 = new ListNode(4);
ListNode n5 = new ListNode(5);
n1.next = n2;
n2.next = n3;
n3.next = n4;
n4.next = n5;
System.out.println(hasCycleByPoint(n1));
System.out.println(getEntranceNode(n1));
}
private static void test3() {
ListNode n1 = new ListNode(1);
ListNode n2 = new ListNode(2);
ListNode n3 = new ListNode(3);
ListNode n4 = new ListNode(4);
ListNode n5 = new ListNode(5);
n1.next = n2;
n2.next = n3;
n3.next = n4;
n4.next = n5;
System.out.println(getFirstCommonNode(n1, n2).val);
}
}
|--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
- 递归翻转链表
答:什么是链表的翻转:给定链表 head–>4—>3–>2–>1,将其翻转成 head–>1–>2–>3–>4 。
首先我们要查看翻转链表是否符合递归规律:问题可以分解成具有相同解决思路的子问题,子子问题…,直到最终的子问题再也无法分解。
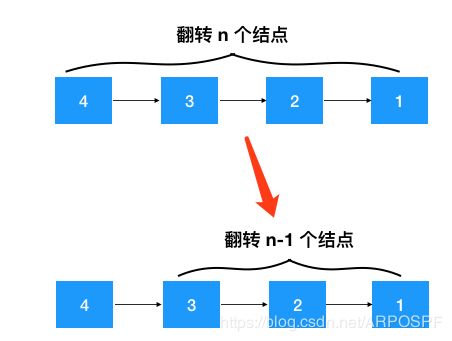
要翻转 head—>4—>3–>2–>1 链表,不考虑 head 结点,分析 4—>3–>2–>1,仔细观察我们发现只要先把 3–>2–>1 翻转成 3<----2<----1,之后再把 3 指向 4 即可(如下图示)

图:翻转链表主要三步骤
只要按以上步骤定义好这个翻转函数的功能即可, 这样由于子问题与最初的问题具有相同的解决思路,拆分后的子问题持续调用这个翻转函数即可达到目的。
注意看上面的步骤1,问题的规模是不是缩小了(如下图),从翻转整个链表变成了只翻转部分链表!问题与子问题都是从某个结点开始翻转,具有相同的解决思路,另外当缩小到只翻转一个结点时,显然是终止条件,符合递归的条件!之后的翻转 3–>2–>1, 2–>1 持续调用这个定义好的递归函数即可!
注意翻转之后 head 的后继节点变了,需要重新设置!别忘了这一步
1、定义递归函数,明确函数的功能。根据以上分析,这个递归函数的功能显然是翻转某个节点开始的链表,然后返回新的头节点。
2、寻找递推公式。上文中已经详细画出了翻转链表的步骤,简单总结一下递推步骤如下:
- 针对节点node(值为4),先翻转node之后的结点,invert(node->next),翻转之后4->3->2->1变成了4->3<-2<-1
- 再把node节点的下个节点(3)指向node,node的后继节点设置为空(避免形成环),此时变成了4<-3<-2<-1
- 返回新的头结点,因为此时新的头节点从原来的4变成了1,需要重新设置一下head
3、将递推公式代入第一步定义好的函数中(invertLinkedList)
4、计算时间/空间复杂度。由于递归调用了n次invertLinkedList函数,所以时间复杂度虽然是O(n)。空间复杂度呢?没有用到额外的空间,但是由于递归调用了n次invertLinkedList函数,压了n次栈,所以空间复杂度也是O(n)。
递归一定要从函数的功能去理解,从函数的功能看,定义的递归函数清晰易懂,定义好了之后,由于问题与被拆分的子问题具有相同的解决思路,所以子问题只要持续调用定义好的功能函数即可,切勿层层展开子问题!

补充:非递归翻转链表(迭代解法)
递归比较容易造成栈溢出,所以如果有其他时间/空间复杂度相近或更好的算法,应该优先选择非递归的解法,对于该问题,主要思路如下:
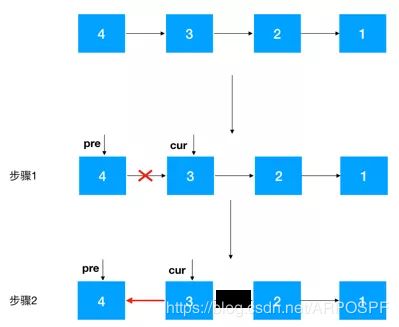
步骤1,定义两个结点,pre,cur,其中cur是pre的后继结点,如果是首次定义,需要把pre指向cur的指针去掉,否则由于之后链表翻转,cur会指向pre,就进行了一个环(如下),这一点需要注意:
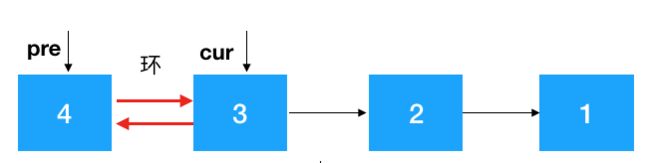
步骤2,知道了cur和pre,翻转就容易了,把cur指向pre即可,之后把cur设置为pre,cur的后继结点设置为cur一直往前重复此步骤即可。注意:同递归翻转一样,迭代翻转完了之后 head 的后继结点从 4 变成了 1,记得重新设置一下。
/**
* 迭代翻转
*/
public void iterationInvertLinkedList() {
// 步骤 1
Node pre = head.next;
Node cur = pre.next;
pre.next = null;
while (cur != null) {
/**
* 务必注意:在 cur 指向 pre 之前一定要先保留 cur 的后继结点,不然 cur 指向 pre 后就再也找不到后继结点了
* 也就无法对 cur 后继之后的结点进行翻转了
*/
Node next = cur.next;
cur.next = pre;
pre = cur;
cur = next;
}
// 此时 pre 为头结点的后继结点
head.next = pre;
}
用迭代的思路来做由于循环了 n 次,显然时间复杂度为 O(n),另外由于没有额外的空间使用,也未像递归那样调用递归函数不断压栈,所以空间复杂度是 O(1),对比递归,显然应该使用迭代的方式来处理!
完整代码如下:
public class LinkedList {
int length = 0; //链表长度,非必须
Node head = new Node(0); //哨兵节点
public void addNode(int val) {
Node tmp = head;
while (tmp.next != null) {
tmp = tmp.next;
}
tmp.next = new Node(val);
length++;
}
public void printList() {
head = this.head.next;
do {
System.out.println(head.data);
head = this.head.next;
} while (this.head != null);
}
public void headInsert(int val) {
// 1. 构造新节点
Node newNode = new Node(val);
//2. 新节点指向头节点之后的节点
newNode.next = head.next;
// 3. 头节点指向新节点
head.next = newNode;
length++;
}
/**
* 删除指定的结点
*
* @param deletedNode
*/
public void removeSelectedNode(Node deletedNode) {
// 如果此结点是尾结点,我们还是要从头节点遍历到尾结点的前继结点,再将尾结点删除
if (deletedNode.next == null) {
Node tmp = head;
while (tmp.next != deletedNode) {
tmp = tmp.next;
}
//找到尾结点的前继结点
tmp.next = null;
} else {
Node nextNode = deletedNode.next;
//将删除结点的后继节点的值赋给被删除结点
deletedNode.data = nextNode.data;
//将nextNode结点删除
deletedNode.next = nextNode.next;
nextNode.next = null;
}
}
/**
* 递归翻转结点node开始的链表
*
* @param node
* @return
*/
public Node invertLinkedList(Node node) {
if (node.next == null) {
return node;
}
// 步骤1:先翻转node之后的链表
Node newHead = invertLinkedList(node.next);
// 步骤2:再把原node节点后继节点的后继节点指向node(4),node的后继节点设置为空(防止形成环)
node.next.next = node;
node.next = null;
// 步骤3:返回翻转后的头节点
return newHead;
}
/**
* 迭代式翻转链表
*/
public void iterationInvertLinkedList() {
// 步骤1
Node pre = head.next;
Node cur = pre.next;
pre.next = null;
while (cur != null) {
//在cur指向pre之前一定要先保留cur和后继结点
Node next = cur.next;
cur.next = pre;
pre = cur;
cur = next;
}
// 此时pre为头结点的后继结点
head.next = pre;
}
public static void main(String[] args) {
LinkedList linkedList = new LinkedList();
int[] arr = {4, 3, 2, 1};
//头插发构造链表
for (int i = 0; i < arr.length; i++) {
linkedList.addNode(arr[i]);
}
Node newHead = linkedList.invertLinkedList(linkedList.head.next);
//翻转后别忘了设置头结点的后继结点
linkedList.head.next = newHead;
//打印链表
linkedList.printList();
}
}
- 如何用两个栈表示一个队列
答:栈的特点是先入后出,出入元素都是在同一端(栈顶):
入栈:

出栈:

队列的特点是先入先出,出入元素是在不同的两端(队头和队尾):
入队:

出队:

既然我们拥有两个栈,那么我们可以让其中一个栈作为队列的入口,负责插入新元素;另一个栈作为队列的出口,负责移除老元素。
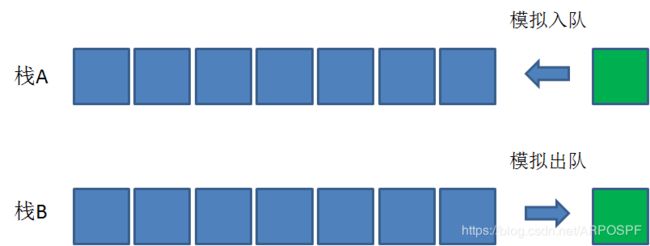
问题:两个栈是各自独立的,怎么能把它们有效关联起来呢?
队列的
主要操作无非有两个:入队和出队
在模拟入队操作时,每一个新元素都被压入到栈A当中。
让元素1“入队”:


让元素2 “入队”:


让元素3“入队”:

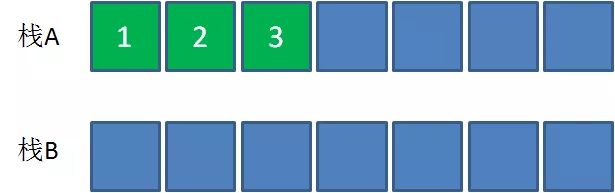
这时候,我们希望最先“入队”的元素1“出队”,需要怎么做呢?
让栈A中的所有元素按顺序出栈,再按照出栈顺序压入栈B。这样一来,元素从栈A弹出并压入栈B的顺序是3,2,1,和当初进入栈A的顺序1,2,3是相反的:
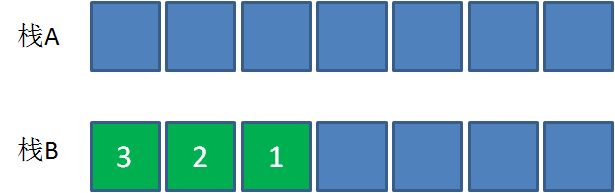
此时让元素1”出队“,也就是让元素1从栈B弹出:

让元素2出栈

这个时候,如果想做入队操作了,只需要重新把新元素压入栈A,此时的出队操作仍然从栈B弹出元素。
如果栈B空了,只要栈A还有元素,就把栈A元素弹出压入栈B。
代码如下:
package DataStructure;
import java.util.Stack;
public class StackforQueue {
private Stack<Integer> stackA = new Stack<>();
private Stack<Integer> stackB = new Stack<>();
/**
* 入队操作
*
* @param element
*/
private void enQueue(int element) {
stackA.push(element);
}
/**
* 出队操作
*
* @return
*/
private Integer deQueue() {
if (stackB.isEmpty()) {
if (stackA.isEmpty()) {
return null;
}
transfer();
}
return stackB.pop();
}
/**
* 将栈A的元素转移到栈B
*/
private void transfer() {
while (!stackA.isEmpty()) {
stackB.push(stackA.pop());
}
}
public static void main(String[] args) {
StackforQueue stackforQueue = new StackforQueue();
stackforQueue.enQueue(1);
stackforQueue.enQueue(2);
stackforQueue.enQueue(3);
System.out.println(stackforQueue.deQueue());
System.out.println(stackforQueue.deQueue());
stackforQueue.enQueue(4);
System.out.println(stackforQueue.deQueue());
System.out.println(stackforQueue.deQueue());
}
}
入队的时间复杂度显然是O(1)。至于出队操作,如果涉及到栈A和栈B的元素迁移,时间复杂度为O(n),如果不用迁移,时间复杂度为O(1)。
- 不用中间元素交换两个元素的方法,(答:使用异或),又问:不使用异或有什么缺点。。
答:这里介绍两个方法,其基本原理就是数的中和。也就是说,通过某种运算(二元运算)将a和b两个数变成一个数,并保存其中一个变量中。然后再通过同样的运算符将a或者b中和掉。这样实际上是利用了a和b本身作为了中间变量。
第一种方法:使用异或,这是利用了异或运算的性质:一个数和两个相同的数异或,值不变。
第二种方法:通过“+”运算符将a和b的运算结果赋给了a(这时a是中间变量)。然后再计算b,这时a的值已经是(a+b)了,因此,a再减b就是原来的a。 而这时b已经是原来的a了,因此,再用运算后的a(实际上是a+b)减运算后的b(实际上是原来的a),就是原来的b了,最后将这个b赋值给a。实际上,我们还可以使用“*”、“/”等符号来实现同样的效果
全部代码如下:
package DataStructure;
public class Exchange {
public static void main(String[] args) {
int numa = -3;
int numb = -9;
int[] num = exchange3(numa, numb);
System.out.println(num[0] + " " + num[1]);
}
/**
* 利用异或交换
* @param numa
* @param numb
* @return
*/
private static int[] exchange1(int numa, int numb) {
int[] num = new int[2];
numa = numa ^ numb;
numb = numa ^ numb;
numa = numa ^ numb;
num[0] = numa;
num[1] = numb;
return num;
}
/**
* 利用加减法交换
* @param numa
* @param numb
* @return
*/
public static int[] exchange2(int numa, int numb) {
int[] num = new int[2];
numa = numa + numb;
numb = numa - numb;
numa = numa - numb;
num[0] = numa;
num[1] = numb;
return num;
}
/**
* 利用乘除法交换
* 注意,除数不能为0
* @param numa
* @param numb
* @return
*/
public static int[] exchange3(int numa, int numb) {
int[] num = new int[2];
numa = numa * numb;
numb = numa / numb;
numa = numa / numb;
num[0] = numa;
num[1] = numb;
return num;
}
/**
* 有符号的数值交换
* @param numa
* @param numb
* @return
*/
public static int[] exchange4(int numa, int numb) {
int[] num = new int[2];
// 不同符号
if (numa * numb <= 0) {
numa = numa + numb;
numb = numa - numb;
numa = numa - numb;
} else {
numa = numa - numb;
numb = numa + numb;
numa = numb - numa;
}
num[0] = numa;
num[1] = numb;
return num;
}
}
另外不使用异或的方法存在一些问题,例如①使用中间变量,这种方法需要利用额外的空间存储变量,②使用加减法或乘除法,可能造成溢出。
补充问题:在一个数组中找出唯一一个与数组内任何元素都不相等的一个元素?
答:可以使用异或运算来达到目的,因为问题的前提是数组内只含有一个不与其他元素重复的元素,那么我们便可以利用异或运算的特点来解决此问题。因为相同的元素经过异或运算的结果是0,那么我们**遍历数组内所有的元素,它们进行异或运算,最终得出的结果便是那个唯一不与其他元素重复的元素。**时间复杂度为O(N)。
- 如何多线程改进K大顶堆或小顶堆?
答:堆排序,是利用堆结构进行排序,一般是利用最大堆,即根节点比左右两个子树的节点都大,具体算法步骤如下。
1、创建堆
首先将数组中的元素调整成堆(对应下面程序中的createHeap(List list)方法)。创建堆就是从树中最后一个非叶子节点(下标为(n-1)/2)开始调整数组中元素的位置,使以这个非叶子节点为根的子树满足堆的结构。即依次将以(n-1)/2、(n-1)/2-1、(n-1)/2-2、…、1、0为根的子树调整为堆。
创建堆主要用了shiftDown操作(对应下面的shiftDown(List list,int parent,int end)方法)。该操作是不断将小元素下调的过程,如果根元素小于左右两个子树的较大者,那么根元素就要跟这个较大者进行交换,直到到达叶子节点为止。siftDown操作每下降一层要比较两次:1)选择左右子树的较大者,2)将较大者跟父结点比较。下降的最大高度即为父节点的高度。由结论:高度为h的满二叉树的所有节点的高度和为n-h-1,高度从0开始,叶子节点高度为0,此结论可由数学归纳法证明,可知最坏情况的比较次数约为2(n-h-1),即创建堆的复杂度度为O(n)。
2、排序
当将数组调整成堆之后,由堆的定义可知,树的根就是最大的元素,这时我们可以将根删除,并将最后一个元素放到根的位置,然后将树重新调整为堆。重新调整为堆之后,根节点又为最大的元素,再删除,再调整,直到元素全部排序。(这里实际上是将最后一个元素和根元素交换,从此以后最后一个元素不在参与树的重新调整,即已经排好序的元素不再参与树的调整)。
shiftDown操作的时间复杂度为O(lgn),即树的高度,排序过程中一共进行了n-1的shiftDown操作,所以可以粗略的推断出堆排序的时间复杂度为O(nlgn)。空间复杂度为O(1)。
3、优化
堆中从根节点到叶节点的一条路径是有序的,最大堆是降序,我们在shiftDown操作时,实际上是在找根节点在某条路径上的一个插入位置,可以借鉴二分的思想,我们可以一次下降到当前高度h的一半的位置(在下降的过程中要将沿途的较大的子节点上移,这样在h/2高度形成空位),即h/2,再比较在一半高度h/2的节点与根节点的大小,如果比根节点大则继续寻找当前一半高度位置的元素即h/4,依次类推,如果当前高度的元素比根节点小,我们就引入shiftUp操作,即将根节点再上移,但由前面的分析可知,上移的次数是有限的,这样就将shiftDown的复杂度变为O(lglgn),堆排序的总体复杂度变为O(n*lglgn)。
代码如下:
import java.util.Arrays;
import java.util.List;
/**
* 创建最大堆,并进行排序
*/
public class HeapSortAdvance {
public static void main(String[] args) {
HeapSortAdvance hsa = new HeapSortAdvance();
List<Integer> list = null;
list = Arrays.asList(3, 0, 23, 6, 5, 43, 23, 566, 67, 34, 2, 56, 98, 42, 49);
hsa.createHeap(list);
hsa.sort(list);
for (int i = 0; i < list.size(); i++) {
System.out.println(list.get(i) + " ");
}
}
/**
* 创建堆,从第一个非孩子结点开始调整,创建一个最大堆
*
* @param list
*/
private List<Integer> createHeap(List<Integer> list) {
int n = list.size();
for (int k = (n - 1) / 2; k >= 0; k--) {
shiftDown(list, k, n - 1);
}
return list;
}
/**
* 将以parent为根节点的二叉树调整为堆
*
* @param list
* @param parent
* @param end
*/
private void shiftDown(List<Integer> list, int parent, int end) {
boolean flag = true;
while (parent * 2 + 1 <= end && flag) { // 如果存在左孩子就进行调整
int lchild = parent * 2 + 1;
int max = 0;
if (lchild + 1 <= end) { //表示存在右孩子
int rchild = lchild + 1;
max = list.get(lchild) > list.get(rchild) ? lchild : rchild;
} else {
max = lchild;
}
if (list.get(max) > list.get(parent)) { //有孩子比父亲大
swap(list, max, parent);
parent = max;
} else {
flag = false; //表示孩子都比父亲大,不需要调整了
}
}
}
private void swap(List<Integer> list, int m, int n) {
int temp = list.get(n);
list.set(n, list.get(m));
list.set(m, temp);
}
public void sort(List<Integer> heap) { //排序主过程
int n = heap.size();
int rmd = n - 1;
while (rmd > 0) {
swap(heap, 0, rmd);
shiftDown(heap, 0, rmd - 1);
rmd--;
}
}
}
- 多个有序数组合并为一个
答:首先考虑合并两个有序数组的情况。基本思路如下:
1)如果其中一个数组的元素均大于另一个数组的元素,则可以直接组合,不用拆分。
即:其中一个数组的第一个元素大于或者小于另一个数组的最后一个元素
2)若不满足1)中的情况,则表明数组需要拆分,拆分的方法如下:
①拆分前,默认两个数组以及最终输出数组的索引均为0;
② 两个数组对应索引下的元素进行比较,小的一方放入最终数组中的当前索引下的位置,并使小的一方数组的索引+1;
③检查是否有数组已经遍历完毕,若有(即该数组的元素已经完全分配到结果数组中),则将另一个数组的剩余元素依次放入最终数组中,直接输出即可。
④最终数组的索引+1,并重复②,直到两个数组均完成索引任务。
代码如下:
public class MyClass {
public static void main(String[] args) {
int[] num1 = new int[]{1, 2, 4, 6, 7, 123, 411, 5334, 1414141, 1314141414};
int[] num2 = new int[]{0, 2, 5, 7, 89, 113, 5623, 6353, 134134};
//变量用于存储两个集合应该被比较的索引(存入新集合就加一)
int a = 0;
int b = 0;
int[] num3 = new int[num1.length + num2.length];
for (int i = 0; i < num3.length; i++) {
if (a < num1.length && b < num2.length) { //两数组都未遍历完,相互比较后加入
if (num1[a] > num2[b]) {
num3[i] = num2[b];
b++;
} else {
num3[i] = num1[a];
a++;
}
} else if (a < num1.length) { //num2已经遍历完,无需比较,直接将剩余num1加入
num3[i] = num1[a];
a++;
} else if (b < num2.length) { //num1已经遍历完,无需比较,直接将剩余num2加入
num3[i] = num2[b];
b++;
}
}
System.out.println("排序后:" + Arrays.toString(num3));
}
}
然后,我们考虑如何合并K个有序数组。最简单的方法是创建一个N大小的数组,然后把所有的数字拷贝进去,然后在进行时间复杂度为O(NlogN)的排序算法,这样总体时间复杂度为O(NlogN)。除此之外,可以利用最小堆完成。时间复杂度为O(NlogK),具体过程如下:
①创建一个大小为N的数组保存最后的结果
②数组本身已经是从大到小的排序,所以我们只需要创建一个大小为K 的最小堆,堆中的初始元素为K个数组中的每个数组的第一个元素,每次从堆中取出最小元素(堆顶元素),并将其存入输出数组中,将堆顶元素所在行的下一个元素加入堆,重新排列堆顶元素,时间复杂度为logK,总计N个元素,所以总体时间复杂度是NlogK
在O(NlogK)的时间复杂度内完成:
- N是所有数组包含的整数个数
- k是数组的个数
除此之外,还可以使用**分治法下的归并。**合并两个有序数组直接使用merge即可,而合并k个可以将其看作两部分,左边合并后的结果与后边合并后的结果,然后再merge。递归的出口是lr,代表只有一个有序数组直接返回,l+1r,代表刚好有两个有序数组直接merge。
代码如下:
package DataStructure;
import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Queue;
class Element {
public int row, col, val;
Element(int row, int col, int val) {
this.row = row;
this.col = col;
this.val = val;
}
}
public class MergeTwoArray {
public static void main(String[] args) {
//定义K个一维数组
int[][] array = {{1, 4, 7, 8, 12, 16, 20}, {2, 5, 7, 9, 10, 25}, {3, 6, 11, 13, 17, 18}};
int[] merged = mergedKSortedArray(array); // 使用最小堆
int[] merged2 = mergedKSortedArray2(array); //使用归并法
System.out.println(Arrays.toString(merged));
System.out.println(Arrays.toString(merged2));
}
/**
* 方法1:使用最小堆
* @param array
* @return
*/
private static int[] mergedKSortedArray(int[][] array) {
if (array == null) {
return new int[0];
}
int totalSize = 0;
//默认由小到大排序
Queue<Element> queue = new PriorityQueue<Element>(array.length, ElementComparator);
//初始化
//把每一行的第一个元素加入PriorityQueue
//统计元素总量
for (int i = 0; i < array.length; i++) {
//当前行长度不为0
if (array[i].length > 0) {
Element element = new Element(i, 0, array[i][0]);
queue.add(element);
totalSize += array[i].length;
}
}
int[] result = new int[totalSize];
int index = 0;
while (!queue.isEmpty()) {
Element element = queue.poll();
result[index++] = element.val;
//当前结点被PriorityQueue跑出来后,当前行的第二个结点加入PriorityQueue
if (element.col + 1 < array[element.row].length) {
element.col += 1;
element.val = array[element.row][element.col];
queue.add(element);
}
}
return result;
}
private static Comparator<Element> ElementComparator = new Comparator<Element>() {
@Override
public int compare(Element left, Element right) {
return left.val - right.val;
}
};
/**
* 方法2:使用分治法下的归并
* @param array
* @return
*/
private static int[] mergedKSortedArray2(int[][] array) {
if (array == null) {
return new int[0];
}
return helper(array, 0, array.length - 1);
}
private static int[] helper(int[][] array, int l, int r) {
if (l == r) {
return array[l];
}
if (l + 1 == r) {
return merged2Array(array[l], array[r]);
}
int mid = l + (r - l) / 2;
int[] left = helper(array, l, mid);
int[] right = helper(array, mid + 1, r);
return merged2Array(left, right);
}
private static int[] merged2Array(int[] a, int[] b) {
int[] res = new int[a.length + b.length];
int i = 0, j = 0;
for (int k = 0; k < res.length; k++) {
if (i >= a.length) {
res[k] = b[j++];
} else if (j >= b.length) {
res[k] = a[i++];
} else if (a[i] < b[j]) {
res[k] = a[i++];
} else {
res[k] = b[j++];
}
}
return res;
}
}
- 顺时针打印数组
答:顺时针打印,分为四个步骤:从左到右,从上到下,从右到左,从下到上。问题的关键在于如果打印中矩阵只剩下一个数字,只有一行,只有一列的情况,该如何控制?这里设置四个参数:left、right、top、buttom,边界处理过程如下:
①从左到右,第一步是需要的,判断left是否小于right;
②从上到下,终止行要大于起始行,即buttom>top
③从右到左,至少有两行两列才会执行,也就是right>left&&buttom>top
④从下到上,至少有三行两列才会执行第四步;即right>left&&buttom-1>top.
代码如下:
package DataStructure;
import java.util.Arrays;
public class SortPringMatrix {
public static void main(String[] args) {
int[][] matrix = {
{57, 50, 59, 18, 31, 13},
{67, 86, 93, 86, 4, 9},
{38, 98, 83, 56, 82, 90},
{66, 50, 67, 11, 7, 69},
{20, 58, 55, 24, 66, 10},
{43, 26, 65, 0, 64, 28},
{62, 86, 38, 19, 37, 98}
};
int[] res = printMatrix(matrix);
System.out.println(Arrays.toString(res));
}
private static int[] printMatrix(int[][] matrix) {
int rows = matrix.length;
int cols = matrix[0].length;
if (matrix == null || rows == 0 || cols == 0) {
System.out.println("");
}
int left = 0;
int right = cols - 1;
int top = 0;
int buttom = rows - 1;
int index = 0;
int[] result = new int[rows * cols];
while (left <= right && top <= buttom) {
// 从左到右
if (left <= right) {
for (int i = left; i <= right; i++) {
//System.out.println(matrix[top][i]);
result[index++] = matrix[top][i];
}
}
//从上到下
if (buttom > top) {
for (int i = top + 1; i <= buttom; i++) {
//System.out.println(matrix[i][right]);
result[index++] = matrix[i][right];
}
}
//从右到左
if (right > left && buttom > top) {
for (int i = right - 1; i >= left; i--) {
//System.out.println(matrix[buttom][i]);
result[index++] = matrix[buttom][i];
}
}
//从下到上
if (buttom - 1 > top && right > left) {
for (int i = buttom - 1; i > top; i--) {
//System.out.println(matrix[i][left]);
result[index++] = matrix[i][left];
}
}
left++;
right--;
top++;
buttom--;
}
return result;
}
}
- 写一个二分查找算法。对于一个有序数组,我们通常采用二分查找的方式来定位某一元素,请编写二分查找的算法,在数组中查找指定元素。
给定一个整数数组A及它的大小n,同时给定要查找的元素val,请返回它在数组中的位置(从0开始),若不存在该元素,返回-1。若该元素出现多次,请返回第一次出现的位置。
测试样例:
[1,3,5,7,9],5,3
返回:1
答:代码如下:
package DataStructure;
public class BinarySearch {
public static void main(String[] args) {
int[] A = {4,4,10,21};
int n = 4;
int val = 4;
int res = binarySearch(A,n,val);
System.out.println(res);
}
private static int binarySearch(int[] A, int n, int val) {
int index = -1;
if (n<=0||A==null){
return index;
}
int mid = 0, left = 0, right = n-1;
while (left<=right){
mid = (left+right)/2;
if (A[mid]>val){
right = mid-1;
}else if (A[mid]<val){
left = mid+1;
}else { // 找到第一个匹配的值
while (mid>=0&&A[mid]==val){
mid--;
}
index = mid+1; //当不满足时跳出循环,因此mid+1
break;
}
}
return index;
}
}
相关问题:LeetCode278:第一个错误的版本
你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, …, n],你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
示例:
给定 n = 5,并且 version = 4 是第一个错误的版本。
调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true
所以,4 是第一个错误的版本。
答:在二分查找中,选取mid的方法一般为mid=[(left+mid)/2]。如果使用的编程语言有整数溢出的情况(例如C++,Java),那么可以用mid=left+[right-left]/2代替前者。
代码如下:
private static int firstBadVersion(int n){
int left = 1;
int right = n;
while (left<right){
int mid = left+(right-left)/2;
if (isBadVersion(mid)){
right = mid;
}else {
left = mid+1;
}
}
return left;
}
注意,这里更好的写法是int mid = (left+right)>>>1;
补充问题:1) 为什么要left+(right-left)/2(答怕溢出);2) int 的最大值是?( 2 31 − 1 = 2147483647 2^{31}-1=2147483647 231−1=2147483647);3) (right-left)/2会不会出现浮点数?(不会);4) 二分查找有什么要求,数组有序,升序降序都可以吗?(要求数组/序列满足一定的有序性);5) 能不能写个代码让升序降序都满足?
答:首先判断数组是否有序:升序或降序,然后根据判断结果执行二分查找。
代码如下:
package DataStructure;
public class BinarySearch {
public static void main(String[] args) {
int val = 4;
int n = 9;
// 升序
int[] A = {1, 2, 4, 4, 9, 10, 15, 17, 21};
System.out.println(binarySearch(A, val));
// 降序
int[] B = {21, 17, 15, 10, 9, 4, 4, 3, 2};
System.out.println(binarySearch(B, val));
// 无序
int[] C = {17, 21, 10, 15, 7, 9, 5, 6, 4};
System.out.println(binarySearch(C, val));
}
/**
* 二分查找
*
* @param array :被查找的数组,默认有序
* @param val:要查找的数
* @return int: 下标位置
*/
private static int binarySearch(int[] array, int val) {
// 1.参数合法性判断
if (null == array || array.length == 0) {
return -1;
}
// 2.判断是否有序,以及升序或者降序
boolean flag1 = false, flag2 = false;
for (int i = 0; i < array.length - 1; i++) {
if (array[i] == Math.min(array[i], array[i + 1])) { //升序
flag1 = true;
} else {
flag1 = false;
break;
}
}
if (!flag1) {
for (int i = 0; i < array.length - 1; i++) {
if (array[i] == Math.max(array[i], array[i + 1])) { //降序
flag2 = true;
} else {
flag2 = false;
break;
}
}
}
if (flag1 || flag2) {
return binarySearch(array, array.length, val, flag1);
}
return -1;
}
private static int binarySearch(int[] array, int n, int val, boolean up) {
int index = -1;
int mid = 0, left = 0, right = n - 1;
while (left <= right) {
mid = left + (right - left) / 2;
if (array[mid] > val) {
if (up) {
right = mid - 1; //升序左移
} else {
left = mid + 1; //降序右移
}
} else if (array[mid] < val) {
if (up) {
left = mid + 1;// 升序右移
} else {
right = mid - 1; //降序右移
}
} else { // 找到第一个匹配的值
while (mid >= 0 && array[mid] == val) {
mid--;
}
index = mid + 1;
break;
}
}
return index;
}
}