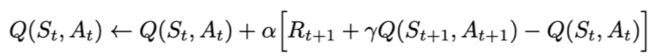强化学习课程学习(5)——基于Q表格的方式求解RL之Model-Free类型的方法
在上一章节主要是阐述了基于模型的方法来求解强化学习的预测问题和控制问题,但是由于动态规划法需要在每一次回溯更新某一个状态的价值时,回溯到该状态的所有可能的后续状态。导致对于复杂问题计算量很大。同时很多时候,我们连环境的状态转化模型 P P P都无法知道,这时动态规划法根本没法使用。这时候我们如何求解强化学习问题呢?由此,model-free类型的方法就产生了,其中常见的方法是:蒙特卡罗(Monte-Calo, MC)、SARSA、Q-learning.
蒙特卡洛(MC)求解
蒙特卡洛法是一种通过采样近似求解问题的方法,即通过采样若干经历完整的状态序列来估计状态的真实价值。所谓的经历完整就是这个序列必须是达到终点的。比如下棋问题分输赢、驾车问题会成功达到终点或者失败。但这种方法和动态规划相比,它有两个特点:
- 不需要依赖模型状态转化概率;
- 需要经历完整的序列学习,完整的经历越多,学习效果越好。
强化学习预测问题的求解
通过蒙特卡洛求解强化学习预测问题的方法实际上也是一种策略评估方法,即给定策略 π \pi π的完整有 T T T状态的状态序列如下:
S 1 , A 1 , R 2 , S 2 , ⋅ ⋅ ⋅ , S t , A t , R t + 1 , ⋅ ⋅ ⋅ R T , S T S_1,A_1,R_2,S_2, \cdot \cdot \cdot,S_t,A_t,R_{t+1},\cdot \cdot \cdot R_T,S_T S1,A1,R2,S2,⋅⋅⋅,St,At,Rt+1,⋅⋅⋅RT,ST
根据价值函数可知:
v π ( s ) = E π ( G t ∣ S t = s ) = E π ( R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋅ ⋅ ⋅ ∣ S t = s ) v_{\pi}(s) = E_{\pi}(G_t|S_t=s) = E_{\pi}(R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}+\cdot \cdot \cdot | S_t = s) vπ(s)=Eπ(Gt∣St=s)=Eπ(Rt+1+γRt+2+γ2Rt+3+⋅⋅⋅∣St=s)
由此可以看出,每个价值函数等于该状态收获的期望,同时这个收获是通过后续奖励与对应的衰减乘积求和得到,那么对于蒙特卡罗法来说,如果要求某一个状态的状态价值,只需要求出所有完整序列中该状态出现时候的收获再取平均值即可近似求解,即:
G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋅ ⋅ ⋅ γ T − t − 1 R T v π ( s ) ≈ a v e r a g e ( G t ) , s . t . S t = s G_t = R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}+\cdot \cdot \cdot \gamma^{T-t-1}R_T \\ v_{\pi}(s) \approx average(G_t), s.t. S_t = s Gt=Rt+1+γRt+2+γ2Rt+3+⋅⋅⋅γT−t−1RTvπ(s)≈average(Gt),s.t.St=s
其优化的点主要体现在以下两个方面:
- 如果同一个状态可能在一个完整序列中出现多次,那么这个状态可以使用两种策略来优化——第一种仅把序列中第一次出现该状态的时收获值纳入平均值计算中;另一种是针对一个状态序列中每次出现的该状态,都计算着对应的收获值并纳入到收获平均值中。正好对应蒙特卡罗法的:
首次访问(first visit)和每次访问(every visit). - 累积更新平均值。average需要保存所有该状态的收获值和最后取平均,这样比较浪费空间,可以在每次迭代计算收获值,每次保存上一轮迭代得到的收获值与次数,当计算当前轮数的收获值时,即可以计算当前收获均值和次数。
强化学习控制问题的求解
蒙特卡洛法求解控制问题的思路和求解动态规划的思路类似,即每次迭代先做策略评估,计算出价值 v k ( s ) v_k(s) vk(s),然后基于贪心法更新当前的策略 π \pi π,最后得到最优价值函数 v ∗ v_{*} v∗和最优策略 π \pi π。
但是也有不同的地方,体现在以下三点:
- 预测问题的策略评估不同;
- 蒙特卡洛法一般是优化最优化动作价值函数,而不是价值状态函数;
- 动态规划一般是基于贪心法更新策略,而MC采取 ϵ \epsilon ϵ-贪心法策略来更新。
基于MC算法的思路求解强化学习问题,求解方法虽然很灵活,但是需要所有采样序列的完整状态序列,在实际应用中,仍然存在很多的实际问题中确实没有完整的状态序列,那么在这种场景下,MC算法就无法求解。
在线控制策略和离线控制策略
对此,研究学者们提出了时序差分(TD)的求解思路,其思路主要分成off-policy和on-policy。两者主要是的区别在于在线控制一般只有一个策略(常见的是 ϵ \epsilon ϵ-贪心法),而离线控制一般有两个策略,一个负责选择新的动作,另一个用于更新新的价值函数。此处主要是阐述时序差分的在线控制算法SARSA和时序差分的离线控制的Q-learning。

SARSA算法求解强化学习问题
SARSA算法是一种时序差分求解强化学习控制问题的方法,这种方法是基于model-free的,不需要环境状态转化模型,和蒙特卡罗法类似,都是价值迭代,即通过价值函数更新,来更新当前的策略,再根据策略来产生新的状态和即时奖励,进而更新价值函数,直到价值函数和策略函数都收敛。
Sarsa全称是state-action-reward-state'-action',目的是学习特定的state下,特定action的价值Q,最终建立和优化一个Q表格,以state为行,action为列,根据与环境交互得到的reward来更新Q表格,更新公式为:
Sarsa在训练中为了更好的探索环境,采用ε-greedy方式来训练,有一定概率随机选择动作输出。
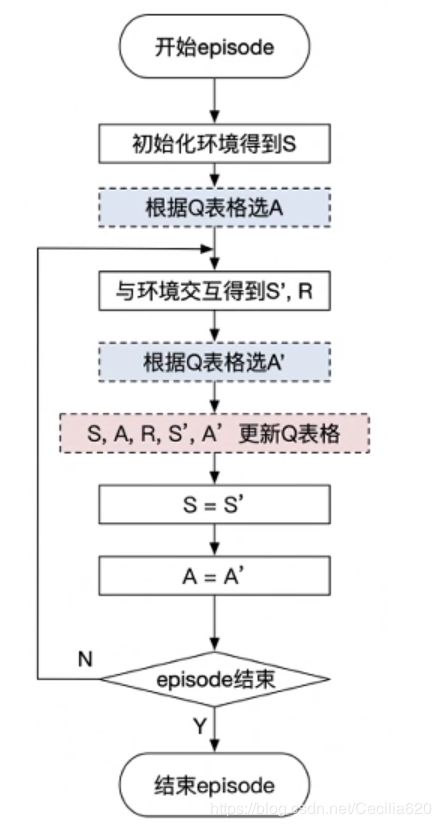
算法流程
SARSA算法实例——悬崖案例
使用Sarsa解决悬崖问题,找到绕过悬崖通往终点的路径————————————————————————————————————
导入依赖后,可以构造Agent
Agent是和环境environment交互的主体。predict()方法:输入观察值observation(或者说状态state),输出动作值sample()方法:再predict()方法基础上使用ε-greedy增加探索learn()方法:输入训练数据,完成一轮Q表格的更新
核心代码如下:
# agent.py
class SarsaAgent(object):
def __init__(self, obs_n, act_n, learning_rate=0.01, gamma=0.9, e_greed=0.1):
self.act_n = act_n # 动作维度,有几个动作可选
self.lr = learning_rate # 学习率
self.gamma = gamma # reward的衰减率
self.epsilon = e_greed # 按一定概率随机选动作
self.Q = np.zeros((obs_n, act_n))
# 根据输入观察值,采样输出的动作值,带探索
def sample(self, obs):
if np.random.uniform(0, 1) < (1.0 - self.epsilon): #根据table的Q值选动作
action = self.predict(obs)
else:
action = np.random.choice(self.act_n) #有一定概率随机探索选取一个动作
return action
# 根据输入观察值,预测输出的动作值
def predict(self, obs):
Q_list = self.Q[obs, :]
maxQ = np.max(Q_list)
action_list = np.where(Q_list == maxQ)[0] # maxQ可能对应多个action
action = np.random.choice(action_list)
return action
# 学习方法,也就是更新Q-table的方法
def learn(self, obs, action, reward, next_obs, next_action, done):
""" on-policy
obs: 交互前的obs, s_t
action: 本次交互选择的action, a_t
reward: 本次动作获得的奖励r
next_obs: 本次交互后的obs, s_t+1
next_action: 根据当前Q表格, 针对next_obs会选择的动作, a_t+1
done: episode是否结束
"""
predict_Q = self.Q[obs, action]
if done:
target_Q = reward # 没有下一个状态了
else:
target_Q = reward + self.gamma * self.Q[next_obs, next_action] # Sarsa
self.Q[obs, action] += self.lr * (target_Q - predict_Q) # 修正q
# 保存Q表格数据到文件
def save(self):
npy_file = './q_table.npy'
np.save(npy_file, self.Q)
print(npy_file + ' saved.')
# 从文件中读取Q值到Q表格中
def restore(self, npy_file='./q_table.npy'):
self.Q = np.load(npy_file)
print(npy_file + ' loaded.')
训练和测试
run_episode():agent在一个episode中训练的过程,使用agent.sample()与环境交互,使用agent.learn()训练Q表格。test_episode():agent在一个episode中测试效果,评估目前的agent能在一个episode中拿到多少总reward。
def run_episode(env, agent, render=False):
total_steps = 0 # 记录每个episode走了多少step
total_reward = 0
obs = env.reset() # 重置环境, 重新开一局(即开始新的一个episode)
action = agent.sample(obs) # 根据算法选择一个动作
while True:
next_obs, reward, done, _ = env.step(action) # 与环境进行一个交互
next_action = agent.sample(next_obs) # 根据算法选择一个动作
# 训练 Sarsa 算法
agent.learn(obs, action, reward, next_obs, next_action, done)
action = next_action
obs = next_obs # 存储上一个观察值
total_reward += reward
total_steps += 1 # 计算step数
if render:
env.render() #渲染新的一帧图形
if done:
break
return total_reward, total_steps
def test_episode(env, agent):
total_reward = 0
obs = env.reset()
while True:
action = agent.predict(obs) # greedy
next_obs, reward, done, _ = env.step(action)
total_reward += reward
obs = next_obs
# time.sleep(0.5)
# env.render()
if done:
break
return total_reward
创建环境和Agent,启动训练
# 使用gym创建悬崖环境
env = gym.make("CliffWalking-v0") # 0 up, 1 right, 2 down, 3 left
# 创建一个agent实例,输入超参数
agent = SarsaAgent(
obs_n=env.observation_space.n,
act_n=env.action_space.n,
learning_rate=0.1,
gamma=0.9,
e_greed=0.1)
# 训练500个episode,打印每个episode的分数
for episode in range(500):
ep_reward, ep_steps = run_episode(env, agent, False)
print('Episode %s: steps = %s , reward = %.1f' % (episode, ep_steps, ep_reward))
# 全部训练结束,查看算法效果
test_reward = test_episode(env, agent)
print('test reward = %.1f' % (test_reward))
SARSA算法和动态规划法比起来,不需要环境的状态转换模型,和蒙特卡罗法比起来,不需要完整的状态序列,因此比较灵活。在传统的强化学习方法中使用比较广泛。但是SARSA算法也有一个传统强化学习方法共有的问题,就是无法求解太复杂的问题。在SARSA算法中, Q ( S , A ) Q(S,A) Q(S,A) 的值使用一张大表来存储的,如果我们的状态和动作都达到百万乃至千万级,需要在内存里保存的这张大表会超级大,甚至溢出,因此不是很适合解决规模很大的问题。当然,对于不是特别复杂的问题,使用SARSA还是很不错的一种强化学习问题求解方法。
Q-learning算法求解强化学习问题
Q-learning也是采用Q表格的方式存储Q值(状态动作价值),决策部分与Sarsa是一样的,采用ε-greedy方式增加探索。Q-learning跟Sarsa不一样的地方是更新Q表格的方式。Sarsa是on-policy的更新方式,先做出动作再更新。Q-learning是off-policy的更新方式,更新learn()时无需获取下一步实际做出的动作next_action,并假设下一步动作是取最大Q值的动作。
Q-learning的更新公式为:
算法流程
Q-learning算法实例——悬崖问题
使用Q-learning解决悬崖问题,找到绕过悬崖通往终端的最短路径,仍然和上述的算法场景类似。
代码大致类似,主要差别在于:
# 学习方法,也就是更新Q-table的方法
def learn(self, obs, action, reward, next_obs, done):
""" off-policy
obs: 交互前的obs, s_t
action: 本次交互选择的action, a_t
reward: 本次动作获得的奖励r
next_obs: 本次交互后的obs, s_t+1
done: episode是否结束
"""
predict_Q = self.Q[obs, action]
if done:
target_Q = reward # 没有下一个状态了
else:
target_Q = reward + self.gamma * np.max(self.Q[next_obs, :]) # Q-learning
self.Q[obs, action] += self.lr * (target_Q - predict_Q) # 修正q
以上所有版本的代码都是基于百度开发的
paddlepaddle和parl框架实现的,版本是paddlepaddle=1.6.3和parl=1.3.1!
感谢百度AI studio提供学习资料和平台,感谢科科老师的讲解!