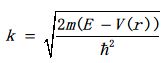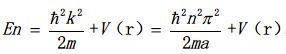固体量子理论初步之能带理论

本文原创，转载需博主同意并注明出处
grin2-固体量子理论初步之能带理论

能带理论讨论晶体状态和载流子运动，是固体性质的最重要的理论基础，也是半导体物理分析必不可少的部分。本文从三个方面探讨固体量子理论的能带理论，了解能带的形成，并了解允带与禁带，导带与价带的相关概念，之后分析具体三种材料的能带结构，最后探讨晶体材料的k空间能带图，了解能量与动量的关系，并了解直接间隙半导体材料和简介间隙半导体材料。

1.能带的形成与相关概念

前面我们利用单电子原子模型学习了量子数和量子态的相关概念，并给出了单电子原子的径向概率密度函数的相关概念。这一小节我们将从单电子原子模型延申，学习能带的形成，允带和禁带的概念，导带和价带的概念以及禁带宽度Eg的概念。

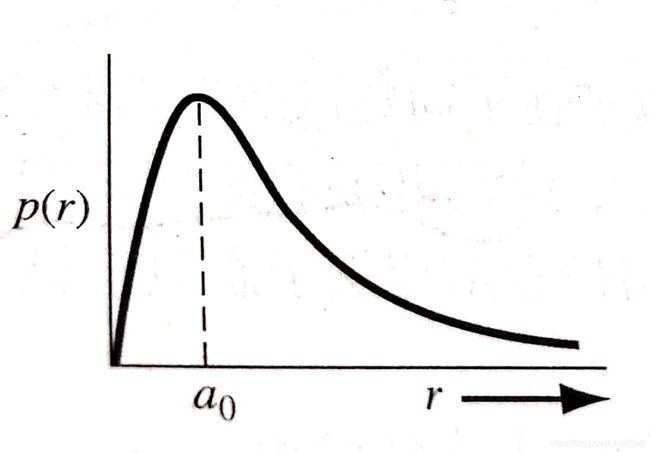
单电子原子的径向概率密度函数如图1所示，在r=a0处，径向概率密度最大，意味着在距离原子核a0的距离处，电子出现的概率最大。我们知道，在单电子原子的讨论中，核外电子处于束缚态（V（r）不为0，而是球型的)

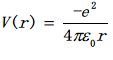
通过计算发现电子能量是量子化的，n是量子态对应的主量子数,能量为

图1 单电子原子的概率密度函数

单电子原子的情况如上所述，下面我们考虑两个单电子原子接近的情况。两个原子接近时，两个原子的势函数相互影响，对三维与时间无关的薛定谔波动方程

V（r）的改变，会影响电子的径向概率密度函数，也就是说对应n=n0的情况下，径向概率密度最大处对应有两个r位置，两个单电子原子相互靠近时的径向概率密度函数相互交叠如图2所示。

图2 两个单电子原子接近时概率密度函数交叠

类比一维情况下的矩形势垒。一维的薛定谔方程

，在外围V=0处，

,边界条件要求波函数而势垒之内波函数连续，有

对应地

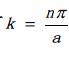
由此得出能量表达式

那么对应势垒之内势函数不为零的部分有：

对应量子化能量

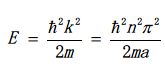
以上推导说明了电子的能量受到势函数影响。因此当两个单电子原子相互靠近时，对应的势函数发生变化，

对应

也就是能量En偏离原来的En0位置。同时，由径向概率密度函数知，n= 对应的径向概率密度最大值有两处，意味着对应的En也有两处

于是出现了所谓的能级分裂。当无数多的电子相互靠近时，对应某个能级（n）就会分化出许多的能量状态En，这些En都是在En0附近分裂出来的，并且差别很小，是准连续的，因此可以认为在这个范围内的能量处都有电子存在，这个能量范围就是能量的允带,如图3所示。其他部分就是能量的禁带，不可能有电子存在。若平衡状态原子间距r0，在此处允带就被禁带隔离开了。

图3 能级分裂

以上分析的是单电子原子相互靠近的情况，多电子原子相互靠近的情况也可以类比分析,下面我们分析多电子原子相互靠近的情况，只考虑原子与原子之间的能级分裂问题，不考虑原子内部的能级分裂问题。大多数原子都有多个能级（n）,对应每个能级又有不同的量子态（nlmms）。我们知道，原子核外电子处在不同的壳层，对应的电子处在不同的能级，具有不同的能量，并且距离核越远的地方,能量越高。当两个原子相互靠近时，最外层的电子会先受到另一个原子的势场的影响（这里指的是一定大小的影响），从而发生能级分裂，原子继续靠近，使内层电子的势场也发生变化，从而内层能级也发生分裂。若平衡状态原子间距r0，那么对应受影响的能级发生分裂形成能带，其他地方不允许能量存在，在r0处能量的允带就被禁带隔离开了，如图4所示。

图4 平衡处r0能带分裂结果

由于原子内部有些能级间距较小，当最外层能级受到其他原子的势场影响形成能带之后，允带宽度增加，可能会与内层能级发生交叠，从而发生交互作用。接下来以Si原子为例，介绍原子内部能级发生交叠从而发生能级杂化的情况。Si原子的元素表示法为：

两个Si原子接近时，其中一个原子的核外电子层受其他电子势场的影响，其3P轨道会发生能带分裂，能量降低，逐渐接近3S轨道直至3S轨道与3P轨道交叠，此时对应的8个量子态处于同一能带中，有4个量子态被电子占据，其他4个量子态为空状态。根据能量最低原理，T=0K时，电子总是有限占据能量低的量子态以使系统能量最低保持系统稳定，因此较低的4个能态被电子占据，组成的能带为价带；4个高能态为空状态，组成的能带为导带，价带顶和导带底之间的能量差就是禁带宽度Eg，如图5所示。

图5 Si外层能级杂化

理解了以上的过程，那么下面给出的概念定义也就很容易理解和辨析了。
能带： 能级分裂形成能带
允带： 允许电子存在的能量范围
禁带： 禁止电子存在的能量范围
价带： T=0K，量子态全部被电子填满的允带
导带： T=0K，量子态全部为空状态的允带
禁带宽度Eg: 允带与允带之间的能量差，即价带顶和导带底的能量差。

2.绝缘体、半导体、金属的能带

不同的材料具有不同的能带结构，不同的能带对应材料的电学特性也不同，这一节我们考虑绝缘体、半导体、金属三种材料的能带情况。
允带中电子的含量决定了材料的导电性。我们知道，材料中电流的形成是因为电荷的定向移动考虑以下五种情况：
（1） 允带中没有电子存在，这种情况下，没有电荷移动，无法形成电流，因此几乎不导电
（2） 允带中有少量电子存在，电子含量少，因此具有一定的导电性，但仍然较小
（3） 允带中有许多电子，由于电子含量高，导电率也较高
（4） 允带中有大量电子，量子态几乎全被占满，这种情况下，电子的移动等价于允带中少量空穴移动，导电率也较低
（5） 允带全被占满，此时电子无法移动，无法形成电流，几乎不导电

室温下，绝缘体导电率十分低，意味着允带中没有能形成电流的电子。根据能带的点穴特性分析，推测出绝缘体的能带情况应该是处于第（1）（5）中情况，也就是外层允带全空（导带全空），内层允带全满（价带全满）,如图6所示

图6 绝缘体价带示意图

室温下，半导体具有一定的导电性，其能带应该满足（2）（4）中的情况，外层允带几乎全空（导带几乎全空），内层允带几乎全满（价带几乎全满）,如图7所示

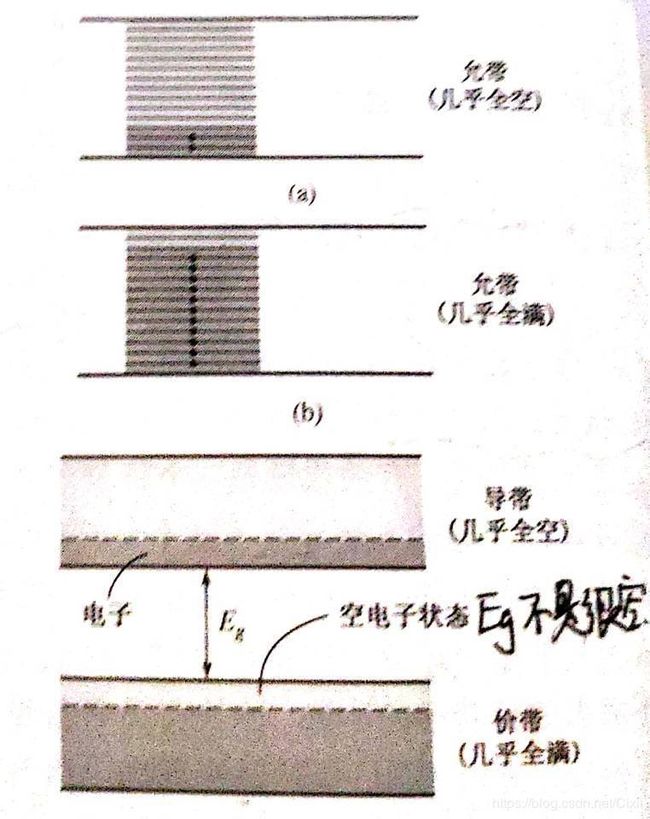
图7 半导体价带示意图

室温下，金属具有良好的导电性，其能带应该满足（3）中的情况，外层允带部分量子态被电子占据（导带半满），内层允带全满（价带全满）如图8所示。若考虑高能带与低能带交叠的情况，那么金属材料的低能带（价带）填充的电子，其能量可能达到高能带（导带）的能量，电子就容易从价带跑到导带上导电,能带交叠的情况主要出现在某些具有金属导电性的氧化物中,如图9所示

图8 金属价带部分填满示意图

图9 金属价带交叠示意图

3.k空间能带图

半导体中晶体分为单晶和多晶，其中多晶也是由许多单晶区域构成，因此我们考虑单晶材料能带的形成，并从数学角度证明。

Kronig-Penny模型通过近似的手段给出了一维单晶的周期性势函数，并对薛定谔方程进行求解，最终给出了方程的求解条件：


下面讨论自由态和束缚态粒子的E-k关系。

故E-k或者E-p为抛物线，如图10所示

图10 自由粒子的E-k关系抛物线曲线

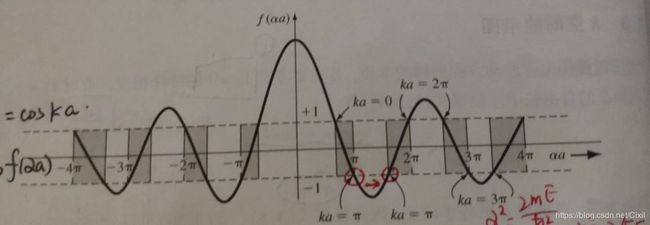
图11 f函数

对应的E-k关系如图12所示

图12 束缚态E-k关系

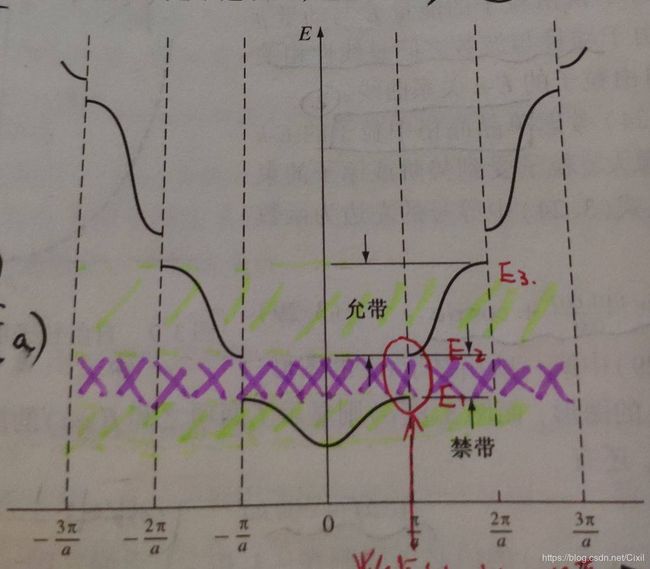
由于单晶材料具有周期性，将不同曲线以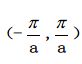
为周期进行平移，该范围内即为E-k的最小正周期，称该范围内的为E-k关系为简约布里渊区，表示简约k空间曲线，如图13所示。

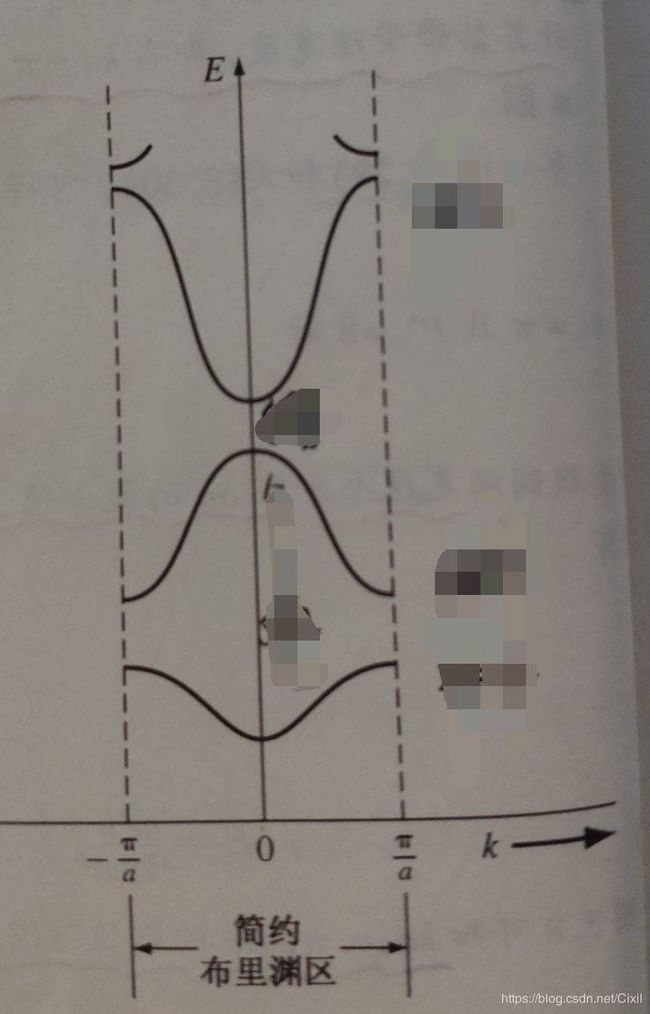
图13 简约布里渊区

图13表示的是同一个晶向的k空间关系图。我们知道，在晶体结构中存在这不同的晶向，不同晶向的原子密度不同，对应的E-k关系也不同。将不同晶向的E-k关系表示在同一张图中，发现价带顶和导带底可能对应为同一个k值(如GaAs)，也可能对应不同的k值（如Si），如图14所示。

图14 GaAs和Si的不同晶向的能带结构

我们知道，

因此，k和p具有线性关系

k值不同就意味着动量不同，E-k关系就类似于E-p关系。价带最大能量处和导带最低能量处具有相同的k坐标，说明材料的电子从价带顶跃迁到导带底时，动量没有发生变化，称这种材料为直接间隙半导体。价带最大能量处和导带最低能量处具有不同的k坐标，说明材料的电子从价带顶跃迁到导带底时，动量发生了变化，且遵守动量守恒定律，称这种材料为间接间隙半导体。