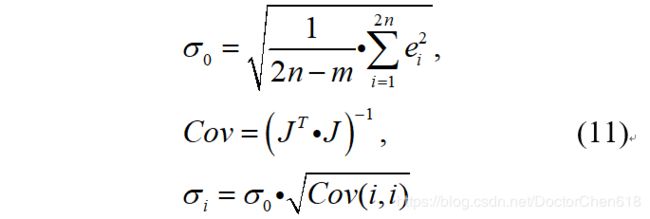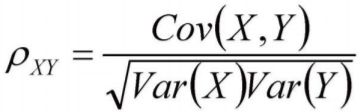光束法平差(BA)之最小二乘求解及协方差矩阵(Covariance)
一.非线性最小二乘优化
1. Introduction
最小值问题(局部或全局)![]()
要求目标函数连续可倒有极值,不是极值问题的要抽象成极值,比如取平方。
极值问题=>求驻点,即![]()
线性问题直接求解,但对于非线性问题因为存在泰勒级数展开时的近似,只能采取从初值x0逐步迭代逼近的方法,即求每一步迭代的改正h。
2.一般形式的
![]()
1)最速下降法(speed descent):在initial stage线性化比较好
![]()
2)Newton法:
在final stage线性化展开,![]()
so,![]()
3)实际问题中常常使用line search或者置信域(trust region)
line search 系数:![]()
3、非线性最小二乘优化形式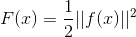
通常f(x)的形式没有极值,需要平方构造得到有驻点的目标函数。主要f(x)与目标方程的区别。最小二乘形式只是一种特殊的形式,如正太分布函数形式也是有驻点的目标函数。
![]()
注意:g和H是F的一阶梯度和海森矩阵,J是f的雅克比Jockey矩阵,H区别与f的海森矩阵。
1)最速下降同上
![]()
2)Gauss-Newton 可以认为newton法在最小二成中的具体化,推导过程相同
![]()
3) LM(Levenberg-Marquardt);通常认为LM比Gauss-Newton更robust。
![]()
4 example: 非线性优化开方
https://blog.csdn.net/songyunli1111/article/details/90474836
#include
using namespace std;
// f(x)=x^2-y
// F(X)=(1/2)f(x)^2
double sqrt_speed_descent_line_search(double y)
{
double x,h;
x = 1.0; //初值
h = 1.0;
double step = 0.01;
// g=F'(X)=f(x)*f'(x)=2x(x^2-y)
while (abs(h) > 0.000001)
{
h = -2 * x *(x*x-y);
x += step*h;
}
return x;
}
double sqrt_GaussNewton_line_search(double y)
{
double x, h;
x = 1.0; //初值
h = 1.0;
double step = 0.01;
// J=f'(x)=2x
// h=-(JTf)/(JTJ)=-f(x)/2x=-(x^2-y)/2x
while (abs(h) > 0.000001)
{
h = -(x*x - y)/(2*x);
x += step*h;
}
return x;
}
int main()
{
double y;
cout << "输入y:" << endl;
while (cin >>y)
{
//double x = sqrt_speed_descent_line_search(y);
double x = sqrt_GaussNewton_line_search(y);
cout << "开方:" << x << endl;
cout << "输入y:" << endl;
}
} 5. NDT求解问题
1)原始算法及PCL 用的Newton法+线搜索(line search);
2)NDT目标方程是非线性优化问题,通常求解不会用最basic的Newton法,常常 是Newton法+line search,或者Newton法+置信域(trust region),可以让该同学加上line search 或者 trust region试试,理论上会提高;
3)目标方程是非线性优化,但不是非线性最小二乘优化形式,并不能直接用 Gauss-Newton+line serch 或者 LM(Levenberg-Marquardt);通常认为LM比Gauss-Newton更robust。但似乎可以改造目标函数使之成为最小二乘问题。
2. 对于NDT求解其实早前我就比较感兴趣的,能否提供给一些比velodyne更稠密精确的TLS、ALS、MLS数据(尽管可以仿真,真实数据效果更方便),我也想做一些更深入的尝试。
3. 附件文档介绍了相关数学知识,清晰明了,可以参考。NDT PCL就对应这个文档的Newton法+(line search)。
二、法方程系数阵\海森矩阵\信息矩阵 H
H*dx=-g
H=JTJ
H的条件数cond(H)决定了方程病态与否。如果H的条件数大,b的微小改变就能引起解x较大的改变,数值稳定性差。如果H的条件数小,b有微小的改变,x的改变也很微小,数值稳定性好
正交矩阵条件数cond(H)=最大特征值/最小特征值。
通常也认为,条件数越大,参数相关性越强,越病态。
三.协方差
1、如何求Covariance
协方差矩阵等于法方程系数阵(H,信息矩阵,海森矩阵)的逆,![]()
参考ceres covariance estimation
2、有什么作用
1)精度评定:待估参数的标准差
analyzing the standard deviation of the estimated parameters with the covariance of the solution is one way to assess the quality of the solution that is returned by a nonlinear least squares solver. Under the assumption that measurement errors are normally distributed, the standard deviation of the i-th estimated parameter is defined as follows [32]:
where represents the root mean squared error that is defined by n, which is the number of control points; m is the number of estimated parameters (3 rotations and 3 translations); and e is the residual of the nonlinear objective function. is called the variance factor and is the unit weight variance or the prior variance factor. represents the Jacobian matrix of the last LM-algorithm iteration, and is the covariance matrix of the estimated parameters.
2)相关系数阵 correlation
四.信息矩阵 information matrix
![]()
在多传感器融合平差处理时,因为不同传感器的精度水平有差异,我们需要根据各传感器的不确定度来设置各误差方程的权重. 这里引入信息矩阵Ω,其值等于协方差矩阵Σ(传感器不确定度)的逆, 协方差的斜对角各项一般为传感器的的标准差. 标准差越小,不确定度越小,越信任,权重越重.