数据结构与算法分析(C语言描述) -- 学习&理解 二叉树

1、树的概念

由根和0个或多个子树构成，子树与跟之间通过线来连接，每一棵子树的父节点叫做根的子节点，可以类似于倒着生长的树的感觉；一般的树可以由多个结点组合，每个结点也可以生成多个子节点，一棵树总共有N个节点和N-1条边构成，因为每个结点总有一条边指向它，root结点不会有边指向；没有儿子结点的称为树叶；由任意结点到根节点的最短路径的描述可以称为深度，一棵树的深度为最深的树叶的深度；

常用的目录结构即为树的应用的一种，可以用c语言结构体描述，包含本节点的描述、本节点的子节点和本节点的下一个兄弟节点；

2、二叉树

二叉树是每一个节点的儿子不能多于两个的树；对于一些特殊类型的树可以称为二叉查找树，平均深度为O(lgN)，即查找的算法平均为O(lgN)，当然这在树的深度很平均的时候，但是有些树的看起来可能就类似于链表的形式，这样树的最大深度为N-1；后面可以通过一些方式来避免这钟情况出现，使树随时保持"平衡"；由于最多只能有两个子节点，所以可称为左结点、右结点和根结点，或者左子树右子树；

 

树的三种遍历方式：

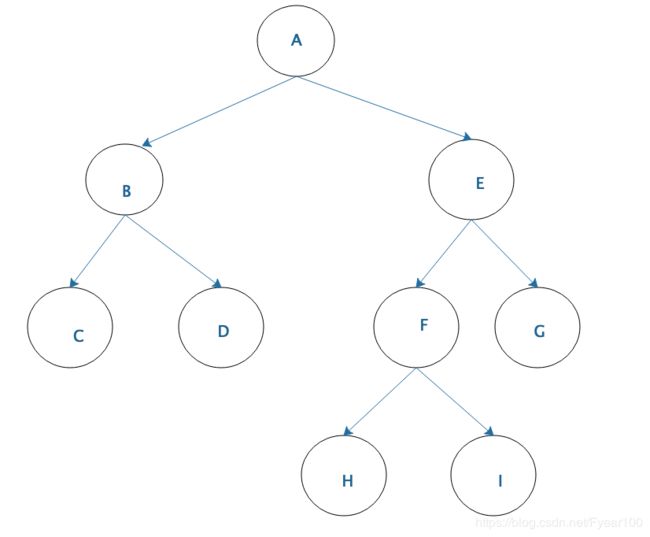
前序遍历：先根结点，再左结点，最后右结点；按照上图的遍历顺序为：ABCDEFHIG

中序遍历：先左结点，再根结点，最后右结点；按照上图的遍历顺序为：CBDAHFIEG

后序遍历：先左结点，再右结点，最后根结点；按照上图的遍历顺序为：CDBHIFGEA

记忆的话就是前中后表示遍历根节点的位置，从左到右，比如前序遍历，就是先根节点再左右结点；

3、二叉查找树

性质1：左结点比根节点小，根节点比右结点大；

那么这样可以很方便的通过通过中序遍历打印出已经排序好的数列；插入和查找操作基本上都是通过element对比找到相应的插入和查找的结点；关于删除的操作会稍微复杂一些，当需要删除的结点是叶子结点时，直接删除即可；

删除叶子结点：

当需要删除的结点有左右子树的时候，虽然有几种方法可行，但是最好用能够使树的深度减少的算法，比如找到需要删除的结点的右子树中最小的数的结点，使当前删除的几点元素值赋值为最小结点的元素值，再删除右子树的最小结点，相当于第一种的删除方式，因为最小结点一定不会有左子树；有些抽象，还是画图直接一点；

删除有左右子树的结点：

    

二叉查找树结构体定义

struct SearchTree
{
	int element;
	struct SearchTree *left;
	struct SearchTree *right;
};

二叉查找树代码示例：

#include 
#include 


struct SearchTree
{
	int element;
	struct SearchTree *left;
	struct SearchTree *right;
};

struct SearchTree *make_empty(struct SearchTree *tree)
{
	if (tree != NULL)
	{
		make_empty(tree->left);
		make_empty(tree->right);
		free(tree);
	}

	return NULL;
}

struct SearchTree *insert_node(struct SearchTree *tree, int element)
{
	if (tree == NULL)
	{
		tree = (struct SearchTree *)malloc(sizeof(struct SearchTree));
		if (tree == NULL)
		{
			printf("malloc failed!\n");
			return NULL;
		}
		else
		{
			tree->element = element;
			tree->left = NULL;
			tree->right = NULL;
			printf("add element : %d success\n", element);
		}
	}
	else if (element < tree->element)
	{
		//printf("element %d < tree->element %d\n", element, tree->element);
		tree->left = insert_node(tree->left, element);
	}
	else if (element > tree->element)
	{
		//printf("element %d > tree->element %d\n", element, tree->element);
		tree->right = insert_node(tree->right, element);
	}
	
	return tree;
}

struct SearchTree *find_node(struct SearchTree *tree, int element)
{
	if (tree == NULL)
	{
		printf("can't find element %d\n", element);
		return NULL;
	}
	else if (element < tree->element)
	{
		//printf("element %d < tree->element %d\n", element, tree->element);
		return find_node(tree->left, element);
	}
	else if (element > tree->element)
	{
		//printf("element %d > tree->element %d\n", element, tree->element);
		return find_node(tree->right, element);
	}
    else if (element == tree->element)
    {
        printf("find element : %d success\n", element);
    }
	
	return tree;
}

struct SearchTree *find_min_node(struct SearchTree *tree)
{
	if (tree == NULL)
	{
		printf("find min node Tree is NULL!\n");
		return NULL;
	}

	if (tree->left == NULL)
	{					
		return tree;	
	}
	else
	{
	
		return find_min_node(tree->left);
	}
}


struct SearchTree *delete_node(struct SearchTree *tree, int element)
{
	struct SearchTree *tree_tmp;
	if (tree == NULL)
	{		
		printf("Tree is NULL\n");	
		return NULL;	
	}
	else if (element < tree->element)
	{
		//printf("element %d < tree->element %d\n", element, tree->element);
		tree->left = delete_node(tree->left, element);
	}
	else if (element > tree->element)
	{
		//printf("element %d > tree->element %d\n", element, tree->element);
		tree->right = delete_node(tree->right, element);
	}
	else
	{
		//two children
		if (tree->right != NULL && tree->left != NULL)
		{
			tree_tmp = find_min_node(tree->right);
			tree->element = tree_tmp->element;
			tree->right = delete_node(tree->right, tree->element);
		}
		//one or zero children
		else
		{
			tree_tmp = tree;
			if (tree->right == NULL)
			{
				tree = tree->left;
			}
			else if (tree->left == NULL)
			{
				tree = tree->right;
			}

			free(tree_tmp);
		}
	}
	
	return tree;
}

int printf_tree_inorder_traversal(struct SearchTree *tree)
{
	if (tree == NULL)
	{
		return 0;
	}

	if (tree->left != NULL)
	{
		printf_tree_inorder_traversal(tree->left);
	}

	printf("%d ", tree->element);

	if (tree->right != NULL)
	{
		printf_tree_inorder_traversal(tree->right);
	}

	return 0;
}

int main(void)
{
	struct SearchTree tree;
    struct SearchTree *tmp_node = NULL;
    
	int num[10] = {3, 4, 1, 10, 8, 6, 9, 15, 12, 14};
	int i;
	
	tree.element = 5;
	tree.left = NULL;
	tree.right = NULL;

	printf("root element : %d\n", tree.element);
	for (i = 0; i < 10; i++)
	{
		insert_node(&tree, num[i]);
	}

	printf_tree_inorder_traversal(&tree);
	printf("\n");

    tmp_node = find_node(&tree, 9);

    if (tmp_node != NULL)
    {
        printf("find element : %d\n", tmp_node->element);
    }

    delete_node(&tree, 10);

    printf_tree_inorder_traversal(&tree);
	printf("\n");

	delete_node(&tree, 9);

    printf_tree_inorder_traversal(&tree);
	printf("\n");


	return 0;
}

当出现相同的元素的时候，可以在node结构体中添加一个count计数，用以表示当前结点代表的数个数；

这样，在删除有代表多个相同element元素的结点时，只需要count--即可，而不用free删除结点的内存空间；