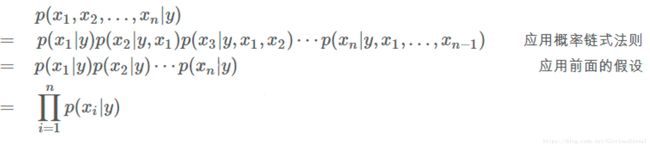2018.09.26朴素贝叶斯算法研究日志

2018.09.26朴素贝叶斯算法研究日志

前些天研究的遗传算法遇到瓶颈，所以转而研究朴素贝叶斯，同时也让自己休息一下，多查询遗传算法的文档然后进一步研究。朴素贝叶斯算法是最简单的一种贝叶斯算法。本文仍然使用Java作为主要语言。

首先给出例题：

算法问题描述：打网球

一个热爱锻炼的人统计了自己打网球与天气等因素的数据，统计表如下，
问：那么他在晴天、凉爽、高湿度和大风的天气时会不会打网球？

Day	Outlook	Temperature	Humidity	Wind	Play Tennis
D1	Sunny	Hot	High	Weak	No
D2	Sunny	Hot	High	Strong	No
D3	Overcast	Hot	High	Weak	Yes
D4	Rain	Mind	High	Weak	Yes
D5	Rain	Cool	Normal	Weak	Yes
D6	Rain	Cool	Normal	Strong	No
D7	Overcast	Cool	Normal	String	Yes
D8	Sunny	Mild	High	Weak	No
D9	Sunny	Cool	Normal	Weak	Yes
D10	Rain	Mild	Normal	Weak	Yes
D11	Sunny	Mild	Normal	Strong	Yes
D12	Overcast	Mild	High	Strong	Yes
D13	Overcast	Hot	Normal	Weak	Yes
D14	Rain	Mild	High	Strong	No

贝叶斯公式

我们给出贝叶斯公式如下：

$$P(Y|X_1,X_2,\cdots ,X_n)=\frac{P(X_1,X_2,\cdots ,X_n|Y)P(Y)}{P(X_1,X_2,\cdots ,X_n)}$$

其中，

• $P(X_1,X_2,\cdots ,X_n|Y)$：似然概率Likelihood
• $P(Y)$：先验概率Prior
• $P(X_1,X_2,\cdots ,X_n)$：归一化常数Normalization Constant

该算法就是根据上述公式预测事件发生的可能性。

朴素贝叶斯

假设前提:

• 各个特征是相互独立的，各个特征出现与其出现的顺序无关，如对于给定的Y和$X_i$之间条件独立；
• 各个特征地位同等重要。

即保证下式成立：

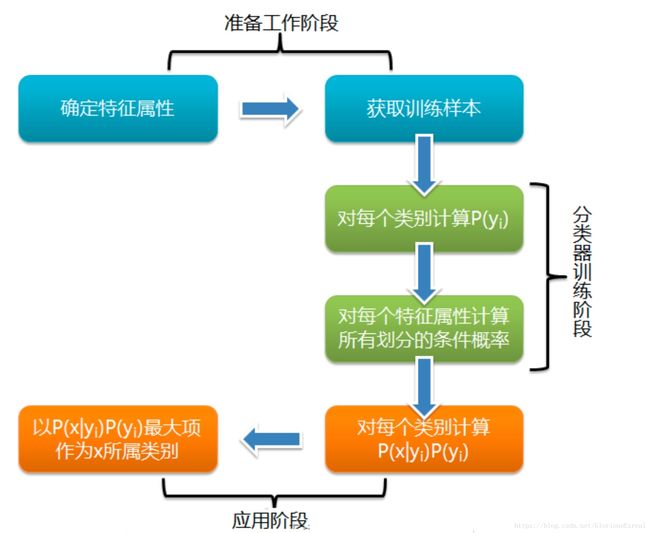
贝叶斯分类过程：

算法描述

确定特征属性、录入训练样本

【Sample.java】

public class Sample {
    /**
     * 数组第一列：
     * 0：Sunny  1：Overcast  2：Rain
     * 数组第二列：
     * 0：Hot    1：Cool  2：Mild
     * 数组第三列：
     * 0：High   1：Normal
     * 数组第四列：
     * 0：Weak   1：Strong
     * 数组第五列：
     * 0：不打球    1：打球
     */
    //int sample[][]={{0,0,0,0,0},{0,0,0,1,0},{1,0,0,0,1},{}};
    int samples[][]={{0,0,1,2,2,2,1,0,0,2,0,1,1,2},
            {0,0,0,2,1,1,1,2,1,2,2,2,0,2},
            {0,0,0,0,1,1,1,0,1,1,1,0,1,0},
            {0,1,0,0,0,1,1,0,0,0,1,1,0,1},
            {0,0,1,1,1,0,1,0,1,1,1,1,1,0}};

    public double[] Prior(){
        Count count = new Count();
        //计算先验概率
        for(int i=0;i<14;i++){
            if (samples[4][i] == 0){
                count.NoPlay++;
            }else{
                count.Play++;
            }
        }
        double[] pPlay=new double[2];
        pPlay[1]=count.Play/14.0;
        pPlay[0]=count.NoPlay/14.0;
        return pPlay;
    }

    public double[][][] Likelihood(){
        Count count = new Count();
        double[][][] likelihood = new double[4][3][2];
        int yes=0,no=0;
        for (int i=0;i<4;i++){
            for (int k=0;k<3;k++){
                for (int j=0;j<14;j++){
                    if (samples[i][j]==k & samples[4][j]==1){
                        yes++;
                    }else if(samples[i][j]==k & samples[4][j]==0){
                        no++;
                    }
                }
                likelihood[i][k][0]=(double)no/count.NoPlay;
                likelihood[i][k][1]=(double)yes/count.Play;
                yes=0;no=0;     //置0
            }
        }
        return likelihood;
    }
}

class Count{
    public int NoPlay,Play;
    Count(){NoPlay=0;Play=0;}
}

【Main.java】

import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        System.out.print("输入第一个条件：");
        int outlook = sc.nextInt();
        System.out.print("输入第二个条件：");
        int temperature = sc.nextInt();
        System.out.print("输入第三个条件：");
        int humidity = sc.nextInt();
        System.out.print("输入第四个条件：");
        int wind = sc.nextInt();

        Sample sample = new Sample();
        double prior[] = new double[2];
        prior = sample.Prior();
        double[][][] likelihood  = new double[4][3][2];
        likelihood = sample.Likelihood();

        double p_Play=prior[1];
        double p_noPlay=prior[0];
        int kind[] = {outlook,temperature,humidity,wind};
        for (int i = 0;i<4;i++){
            for (int j=0;j<4;j++)
                p_Play *= likelihood[i][kind[j]][1];
        }
        for (int i = 0;i<4;i++){
            for (int j=0;j<4;j++)
                p_noPlay *= likelihood[i][kind[j]][0];
        }
        System.out.println("打球的概率为："+p_Play);
        System.out.println("不打球的概率为："+p_noPlay);
        if (p_Play>=p_noPlay){
            System.out.println("这个人今天会打球！");
        }else{
            System.out.println("这个人今天不会打球。");
        }
    }
}