LinearRegression
目录
- 1. 线性回归算法简介
- 2. 机器学习算法的一些概念
- 2.1 目标函数
- 2.2 损失函数
- 2.3 代价函数
- 3. 简单线性回归算法思想
- 3.1 损失函数
- 3.1.1 确定损失函数
- 3.1.2 求损失函数最小化时候的θ参数的方法
- 3.1.3 代价函数(损失函数+正则项)
- 3.2 公式推导
- 4. 多元线性回归思想
- 4.1公式推导(多元线性回归的正规方程解)
- 5. 梯度下降法
- 5.1 梯度下降法简介
- 5.2 梯度下降法求解(使损失函数尽可能小)
- 5.3 三种梯度下降法(BGD、SGD、MBGD)
- 6. 数据集存在多个特征
- 6.1在三维平面,数据集的特征有两个的情况
- 6.2 注意
- 6.3 解决方案
- 7. 线性回归模型评价标准:
- 8. 线性回归推广
- 8.1多项式回归
- 8.2 广义线性回归
- 9. sklearn参数详解
- 10. 问题
- 11. 实现代码
- 12. 参考资料
1. 线性回归算法简介
- 解决回归问题
- 思想简单,容易实现
- 许多强大的非线性模型的基础
- 结果具有很好的可解释性
- 蕴含机器学习中很多重要的思想
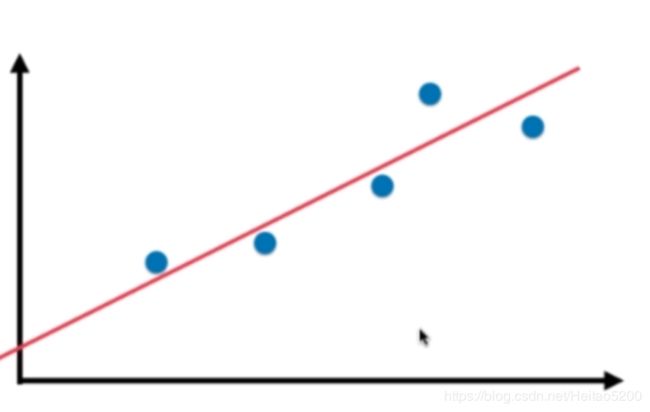
样本特征只有一个的线性回归问题,为简单线性回归。
样本特征有多个的线性回归问题,为多元线性回归。(由此可见,线性并不代表直线)
线性回归算法将无数的训练集数据放在一个坐标系中,以坐标系的一个维度作为label,其他维度作为特征,
最终会发现他们是沿着一条直线分布。线性回归算法的最终目的就是寻找出一条直线、一个面或者体(根据数据的维度而定),最大程度上"拟合"样本特征和输出label之间的关系。
- 特征是一维时,线性模型在二维空间构成一条直线
- 特征是二维时,线性模型在三维空间中构成一个平面
- 特征是三维时,则最终模型在四维空间中构成一个体
- 以此类推…
2. 机器学习算法的一些概念
2.1 目标函数
损失函数(Loss Function )是定义在单个样本上的,算的是一个样本的误差。
2.2 损失函数
代价函数(Cost Function )是定义在整个训练集上的,是所有样本误差的平均,也就是损失函数的平均。
2.3 代价函数
目标函数(Object Function)定义为:最终需要优化的函数。等于经验风险+结构风险(也就是Cost Function + 正则化项)。
注意:
有的地方将损失函数和代价函数没有细分也就是两者等同的。
本文中损失函数=代价函数,目标函数是一个与他们相关但更广的概念,
对于目标函数来说在有约束条件下的最小化就是损失函数(loss function)详情参见
3. 简单线性回归算法思想
在简单线性回归中,我们将训练集特征作为横坐标,训练集label作为纵坐标,那么我们的最终目的就是
寻找出一条直线 y = a x i + b y = ax_i +b y=axi+b当给出新的特征时,我们希望能够带入到 y = a x i + b y = ax_i +b y=axi+b中,求出预测值。
3.1 损失函数
3.1.1 确定损失函数
- 均方误差作为损失函数
3.1.2 求损失函数最小化时候的θ参数的方法
- 最小二乘法
- 最大似然估计
- 梯度下降法
- 牛顿法、拟牛顿法
- 坐标轴下降法
- 最小角回归法
3.1.3 代价函数(损失函数+正则项)
-
L1正则化(L1范数)
L1 正则化通常称为 Lasso 回归,它和一般线性回归的区别是在损失函数上增加了一个 L1 正则化的项,L1 正则化的项有一个常数系数 α 来调节损失函数的均方差项和正则化项的权重,具体 Lasso 回归的损失函数表达式如下:
J ( θ ) = 1 2 n ( X θ − Y ) T ( X θ − Y ) + α ∥ θ ∥ 1 J(\theta) = \frac{1}{2n}(X\theta-Y)^T(X\theta-Y)+\alpha \begin{Vmatrix} \theta \end{Vmatrix}_1 J(θ)=2n1(Xθ−Y)T(Xθ−Y)+α∥∥θ∥∥1其中 n 为样本个数,α 为常数系数,需要进行调优。 ∣ ∣ θ ∣ ∣ 1 ||\theta||_1 ∣∣θ∣∣1 为 L1 范数。
Lasso 回归可以使得一些特征的系数变小,甚至还是一些绝对值较小的系数直接变为 0。增强模型的泛化能力。
Lasso 回归的求解办法一般有坐标轴下降法(coordinate descent)和最小角回归法( Least Angle Regression) -
L2正则化(L2范数)
线性回归的 L2 正则化通常称为 Ridge 回归,它和一般线性回归的区别是在损失函数上增加了一个 L2 正则化的项,和 Lasso 回归的区别是 Ridge 回归的正则化项是 L2 范数,而 Lasso 回归的正则化项是 L1 范数。具体 Ridge 回归的损失函数表达式如下: J ( θ ) = 1 2 n ( X θ − Y ) T ( X θ − Y ) + 1 2 α ∥ θ ∥ 2 2 J(\theta) = \frac{1}{2n}(X\theta-Y)^T(X\theta-Y)+\frac{1}{2}\alpha \begin{Vmatrix} \theta \end{Vmatrix}_2^2 J(θ)=2n1(Xθ−Y)T(Xθ−Y)+21α∥∥θ∥∥22其中 α 为常数系数,需要进行调优 ∣ ∣ θ ∣ ∣ 2 ||\theta||_2 ∣∣θ∣∣2为 L2 范数。
Ridge 回归在不抛弃任何一个特征的情况下,缩小了回归系数,使得模型相对而言比较的稳定,但和 Lasso 回归比,这会使得模型的特征留的特别多,模型解释性差。
Ridge 回归的求解比较简单,一般用最小二乘法。
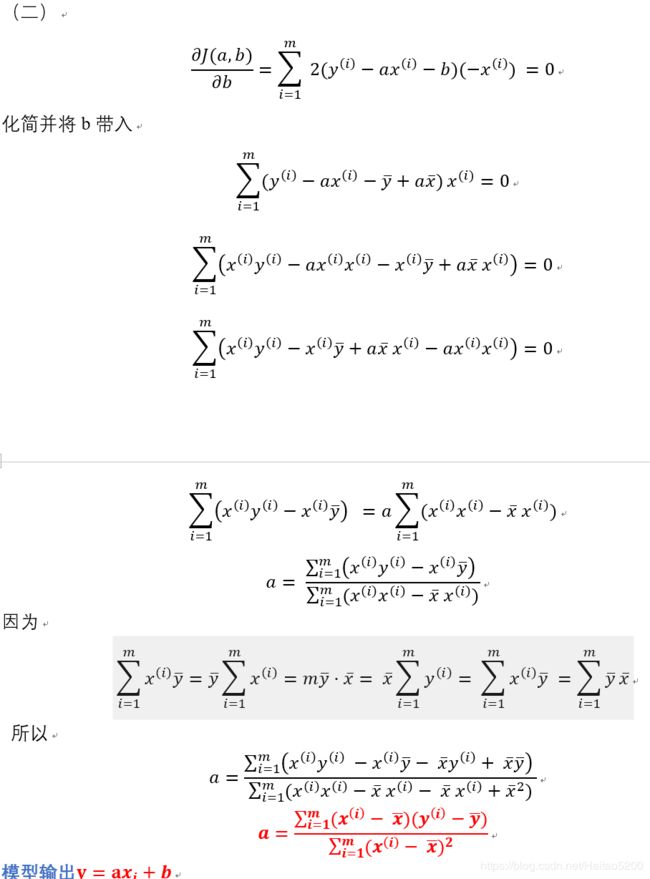
3.2 公式推导
找到a和b使得 ∑ i = 1 m ( y ( i ) − a x ( i ) − b ) 2 \sum_{i=1}^{m} (y^{(i) }- ax^{(i)} -b)^2 ∑i=1m(y(i)−ax(i)−b)2 尽可能小,
这是一个典型的最小二乘法问题:最小化误差的平方
损失函数是计算期望值和预测值的差值,期望其差值(也就是损失)越来越小
4. 多元线性回归思想
在多元线性回归中,我们已经不能再简单地将训练集特征作为横坐标,训练集label作为纵坐标了,
但是我们的最终目的依旧是找到函数找到a和b使得 y ^ ( i ) = X b θ \hat y^{(i)} = X_b \theta y^(i)=Xbθ尽可能小,
当给出新的特征时,我们希望能够带入到 y ^ ( i ) = X b θ \hat y^{(i)} = X_b \theta y^(i)=Xbθ中,
求出预测值。
4.1公式推导(多元线性回归的正规方程解)
5. 梯度下降法
- 梯度下降法不是一个机器学习算法
- 是一种基于搜索的最优化方法(优化目标函数)
- 作用:求目标函数的最小值
- 在求解机器学习算法的模型参数,即无约束优化问题时, 梯度下降(Gradient Descent)是最常采用的方法之一, 另一种常用的方法是最小二乘法
5.1 梯度下降法简介
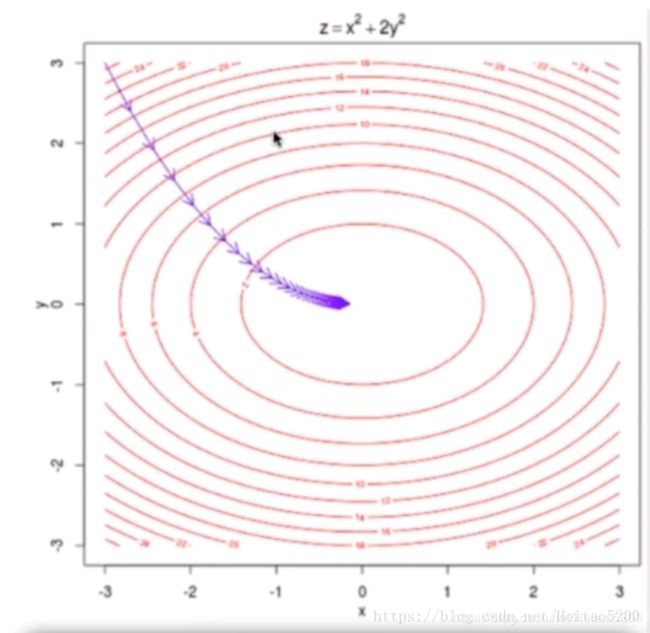
以下是定义了一个损失函数以后,参数 theta 对应的损失函数 J 的值对应的示例图,
我们需要找到使得损失函数值 J 取得最小值对应的 theta(这里是二维平面,也就是说数据集的特征只有一个), 在直线方程中,导数代表斜率; 在曲线方程中,导数代表切线斜率。这里导数即为梯度。

η \eta η称为学习率,它是梯度下降法的一个超参数,它的取值反映获得最优解的速度,取值不合适时甚至得不到最优解。
5.2 梯度下降法求解(使损失函数尽可能小)
-
数据集处理
每个样本增加一个特征 x 0 = 1 x_0 =1 x0=1
( ( x 1 0 ) ( x 2 0 ) ⋯ ( x 4 0 ) ( y 0 ) ( x 1 1 ) ( x 2 1 ) ⋯ ( x 4 1 ) ( y 1 ) ⋯ ( x 1 n ) ( x 2 n ) ⋯ ( x 4 n ) ( y n ) ) ⇒ ( ( x 0 0 ) ( x 1 0 ) ( x 2 0 ) ⋯ ( x 4 0 ) ( y 0 ) ( x 0 1 ) ( x 1 1 ) ( x 2 1 ) ⋯ ( x 4 1 ) ( y 1 ) ⋯ ( x 0 n ) ( x 1 n ) ( x 2 n ) ⋯ ( x 4 n ) ( y n ) ) \begin{pmatrix} &(x_1^0) &(x_2^0) &\cdots &(x_4^0) &(y^0)\\ &(x_1^1) &(x_2^1) &\cdots &(x_4^1) &(y^1)\\ & \cdots \\ &(x_1^n) &(x_2^n) &\cdots &(x_4^n) &(y^n) \end{pmatrix} \Rightarrow \begin{pmatrix} &(x_0^0) &(x_1^0) &(x_2^0) &\cdots &(x_4^0) &(y^0)\\ &(x_0^1) &(x_1^1) &(x_2^1) &\cdots &(x_4^1) &(y^1)\\ & \cdots \\ &(x_0^n) &(x_1^n) &(x_2^n) &\cdots &(x_4^n) &(y^n) \end{pmatrix} ⎝⎜⎜⎛(x10)(x11)⋯(x1n)(x20)(x21)(x2n)⋯⋯⋯(x40)(x41)(x4n)(y0)(y1)(yn)⎠⎟⎟⎞⇒⎝⎜⎜⎛(x00)(x01)⋯(x0n)(x10)(x11)(x1n)(x20)(x21)(x2n)⋯⋯⋯(x40)(x41)(x4n)(y0)(y1)(yn)⎠⎟⎟⎞
有 y ^ ( i ) = θ 0 x 0 ( i ) + θ 1 x 1 ( i ) + θ 2 x 2 ( i ) + ⋯ + θ n x n ( i ) \hat y^{(i)} = \theta _0 x_0^{(i)}+ \theta_1 x_1^{(i)}+ \theta_2 x_2^{(i)}+\cdots + \theta_n x_n^{(i)} y^(i)=θ0x0(i)+θ1x1(i)+θ2x2(i)+⋯+θnxn(i)
-
求解方法
- 代数法
- 矩阵法(向量法)
二者步骤一样:
1.确定损失函数,求其梯度表达式
损失函数:
J ( θ 0 , θ 1 , ⋯ , θ n ) = 1 2 m ∑ i = 1 m ( y ( i ) − y ^ ( i ) ) 2 J(\theta _0,\theta _1,\cdots , \theta _n) = \frac{1}{2m} \sum_{i=1}^{m}(y^{(i)} - \hat y^{(i)})^{2} J(θ0,θ1,⋯,θn)=2m1i=1∑m(y(i)−y^(i))2
= 1 2 m ∑ i = 1 m ( y ( i ) − ( θ 0 x 0 ( i ) + θ 1 x 1 ( i ) + θ 2 x 2 ( i ) + ⋯ + θ n x n ( i ) ) ) 2 = \frac{1}{2m} \sum_{i=1}^{m}(y^{(i)} - (\theta _0 x_0^{(i)}+ \theta_1 x_1^{(i)}+ \theta_2 x_2^{(i)}+\cdots + \theta_n x_n^{(i)} ))^2 =2m1i=1∑m(y(i)−(θ0x0(i)+θ1x1(i)+θ2x2(i)+⋯+θnxn(i)))2
系数 1 2 m \frac{1}{2m} 2m1 是为了方便求偏导
梯度表达式:
∂ J ( θ 0 , θ 1 , ⋯ , θ n ) ∂ θ j = 1 m ∑ i = 1 m ( y ( i ) − y ^ ( i ) ) 2 x j i \frac{\partial J(\theta _0,\theta _1,\cdots , \theta _n)}{\partial \theta _j} = \frac{1}{m}\sum_{i=1}^{m}(y^{(i)} - \hat y^{(i)})^{2}x_j^i ∂θj∂J(θ0,θ1,⋯,θn)=m1i=1∑m(y(i)−y^(i))2xji
2.学习率乘以损失函数的梯度,得到当前位置下降的距离
3.确定是否对于所有的 梯度下降的距离都小于 ,如果小于 则算法终止,当前所有的 即为所求。
4.更新 ,其更新表达式如下。更新完毕后继续转入步骤 1.
-
机器学习算法的一种思路
通过分析问题,确定问题的损失函数,优化损失函数,获得机器学习的模型
5.3 三种梯度下降法(BGD、SGD、MBGD)
-
批量梯度下降法(Batch Gradient Descent)
批量梯度下降法,是梯度下降法最常用的形式,具体做法也就是在更新参数时使用所有的样本来进行更新
更新公式:
-
随机梯度下降法(Stochastic Gradient Descent)
求梯度时没有用所有的 m 个样本的数据,而是仅仅选取一个样本 i 来求梯度
更新公式:
-
小批量梯度下降法(Mini-batch Gradient Descent)
小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷,也就是对于 m 个样本, 采用 x 个样本来迭代,1
**更新公式:**
6. 数据集存在多个特征
6.1在三维平面,数据集的特征有两个的情况
6.2 注意
并不是所有的损失函数用梯度下降法都能够找到全局的最优解,有可能是一个局部最优解。 当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。
6.3 解决方案
- 多次运行,随机化初始点
- 梯度下降法的初始点也是一个超参数
- 设置合适的学习率。一般为0.01
7. 线性回归模型评价标准:
回归评价指标 MSE、RMSE、MAE、R-Squared
skearn中使用的是R-Squared评价
GridSearchCV网格搜索出来的最优超参数使用的评价标准是GridSearchCV里面的score评分,并不是sklearn里面的score评分,sklearn采用的R_Squared评分
8. 线性回归推广
8.1多项式回归
我们之前讨论的线性回归模型 y = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n y=\theta_0 + \theta_1x_1 + \theta_2x_2+\cdots +\theta_nx_n y=θ0+θ1x1+θ2x2+⋯+θnxn
都是x的一次方,如果增加二次方,那么模型就变成了多项式回归。这里写一个只有两个特征的 p 次方多项式回归的模型: y = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 2 + θ 4 x 2 2 + θ 5 x 1 x 2 y=\theta_0 + \theta_1x_1 + \theta_2x_2+ \theta_3x_1^2+\theta_4x_2^2+ \theta_5x_1x_2 y=θ0+θ1x1+θ2x2+θ3x12+θ4x22+θ5x1x2
令 x 0 = 1 , x 1 = x 1 , x 2 = x 2 , x 3 = x 1 2 , x 4 = x 2 2 , x 5 = x 1 x 2 x_0=1,x_1=x_1,x_2=x_2,x_3=x_1^2,x_4=x_2^2,x5=x_1x_2 x0=1,x1=x1,x2=x2,x3=x12,x4=x22,x5=x1x2
得: y = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + θ 4 x 4 + θ 5 x 5 y=\theta_0 + \theta_1x_1 + \theta_2x_2+ \theta_3x_3+\theta_4x_4+ \theta_5x_5 y=θ0+θ1x1+θ2x2+θ3x3+θ4x4+θ5x5
这样我们就将不是线性回归的函数变成了线性回归的函数,这是一个五元一次线性回归。
8.2 广义线性回归
我们的输出 Y 不满足和 X 的线性关系,但是 lnY 和 X 满足线性关系,模型函数如下 l n Y = X θ lnY=X\theta lnY=Xθ
这样对与每个样本的输入 y,我们用 lny 去对应, 从而仍然可以用线性回归的算法去处理这个问题。我们把 Iny 一般化,假设这个函数是单调可微函数 g(.), 则一般化的广义线性回归形式是: g ( Y ) = X ( θ ) 或 者 Y = g − 1 ( X θ ) g(Y)=X(\theta)或者Y=g^{-1}(X\theta) g(Y)=X(θ)或者Y=g−1(Xθ),这个函数 g(.) 我们通常称为联系函数。
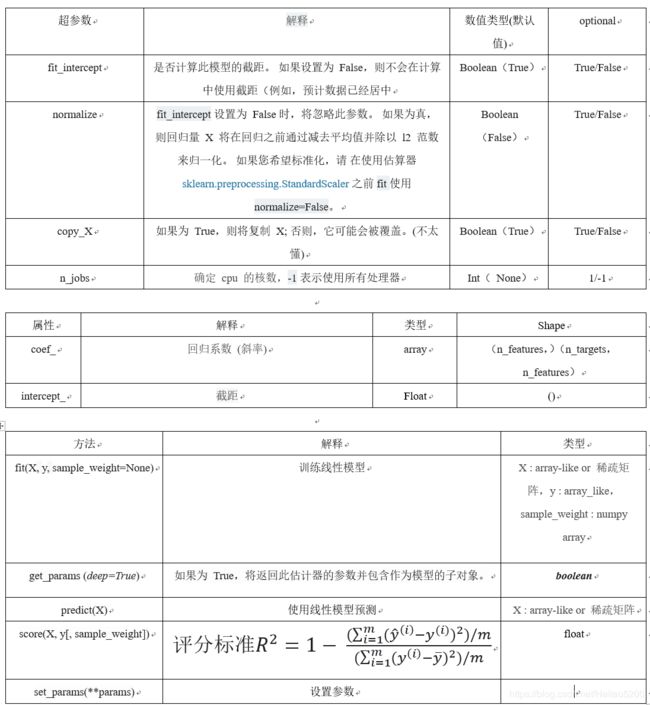
9. sklearn参数详解
10. 问题
- 个人感觉,线性回归的可解释性比较好,大家会把他用作特征选择时的参考吗?具体怎么实现?
sklearn.LinearRegression().coef_属性结果是每个特征的系数,反应正负相关程度
-
线性回归、Ridge回归(L2范式)、Lasso 回归(L1范式)的区别和适用条件;
-
最小二乘法的算法复杂度怎么分析?
在这次整理笔记中收获比较大的是清楚理解了3个问题:——布朗
1.定义损失函数的两种方法:最小二乘和极大似然;
* 最小二乘:真实值和观测值的误差平方和
* 极大似然:我们有一组样本(X,Y),需要估计一个参数theta,让出现(X,Y) 的概率最大; 这种情况下同样能推导出要求误差平方和最小
2.求解代价函数有正规方程和梯度下降,二者比较明显的区别,正规方程是一次计算出结果,当特征量比较大的时候, 矩阵的逆计算量会很大, 这种时候梯度下降也能适合;
3.为什么L1正则化可以产生稀疏模型(L1是怎么让系数等于零的),为什么L2正则化可以防止过拟合?
对代价函数加入L1 和L2 相当于在正则化约束下求出代价函数取最小值的解;
对于L1, 在二维平面上理解为一个矩形, 代价函数与矩形的顶点相交的概率比较大,所以w等于零的概率比较大,产生稀疏矩阵,特征选择
代价函数加入L2, 在梯度下降的时候求得的w会比不加L2小,w越小越能避免出现过拟合情况
11. 实现代码
线性回归算法Demo
12. 参考资料
sklearn-GridSearchCV,CV 调节超参使用方法
Latex公式编辑手册1
Latex在线编辑公式
机器学习算法 - 线性回归————Datawhale
机器学习算法 - 线性回归————爖
numpy.array的基本操作
numpy.hstack和numpy.vstack操作
机器学习算法-线性回归——布朗