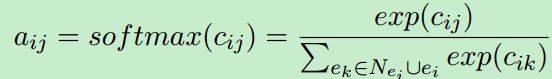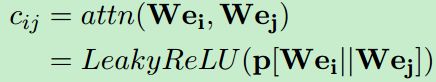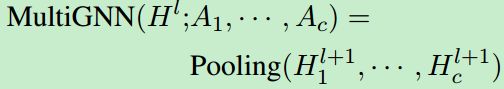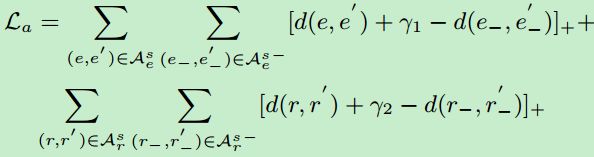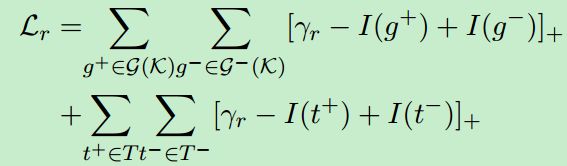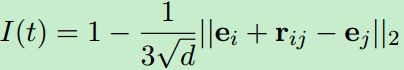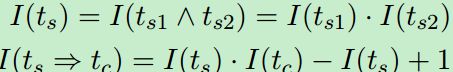Multi-Channel Graph Neural Network for Entity Alignment
原文地址:https://arxiv.org/pdf/1908.09898v1.pdf
0摘要
实体对齐往往受结构异质性及有限的种子对的约束。本文提出多通道图神经网络MUGNN来学习面向对齐的知识图谱嵌入,通过多个通道鲁棒地编码两个知识图谱。每个通道通过不同的关系权重模式来编码KG,以同时完成两个任务:基于自注意力的KG补全和跨语言注意力的实体修剪。另外,还在两个KG中进行规则知识的推理和转移。
1简介
知识图谱以有向图的形式存储知识,节点表示实体,边表示关系。从知识图谱的概念提出以来,很多知识图谱被提出来为不同的应用和语言提供结构化的知识。这些KG往往包含互补的内容,很多学者试着将这些互补的KG融合到一起以更好地服务于知识驱动的下游任务,如信息抽取和推荐系统。
对齐两个KG并不是件容易的事,因为它们有不同的表面形式,这使得基于符号的方法往往效果不好。另外,最近的工作利用一般的知识图谱嵌入方法并基于一些种子对将实体嵌入到同一空间。这一方法的假设是,实体与其等价实体应该有相似的结构从而有相似的嵌入。然而目前的对齐性能并不如人意,主要是有以下挑战:
1)结构的异质性: 不同的KG往往在很多方面都不一样,可能会从根本上错失了表示学习和对齐信息。
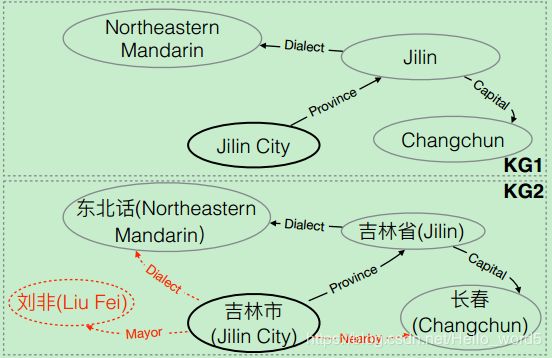
例如下图中的实体‘Jilin City’,这两个图分别表示从中文和英文维基百科中抽取的关于它的子图。由于它是个中国城市,所以KG2比KG1包含更多关于它的信息。
现有的基于一般嵌入方法的对齐模型严重依赖于种子对齐做为训练数据,而种子对往往数量有限。GCN 通过建模结构特征能加强实体嵌入,但是没有考虑结构异质性。
为了解决这一问题,本文提出同时执行知识推理和对齐,以显式地调节不同KG的结构差异,并医用基于图的模型来充分利用对齐信息。结构调节的基本思想是,补全缺失的关系并修剪多余的实体。如上图所示,为了调节 Jinlin City 的结构差异性,首先补全KG1中缺失的关系‘Dialect’和‘Nearby’,并过滤掉KG2中的额外实体‘Liu Fei’. KG不完整的天然属性和构建的目的共同导致了不对称的实体和关系。
本文提出多通道图神经网络MuGNN,它能同时编码不同的KG来学习面向对齐的嵌入。对于每个KG,MuGNN利用不同的面向KG补全和修剪的通道,以调节两种类型的结构差异:缺失的关系和多余的实体。不同的通道通过池化技术相结合,这样实体嵌入就能被来自不同视角的调节后的结构做增强,提高种子对齐的利用效率。每个通道通过共享参数在两个KG中转移结构知识。
具体而言,对于KG补全,先用AMIE+从每个KG中抽取规则,然后在KG间进行规则传递。类似于GAT,本文利用KG自注意力来对每个GNN通道上的关系进行加权。为了对KG进行修剪,设计跨KG的注意力通过为对于关系分配低的权重来过滤多余的实体。主要贡献总结如下:
1)提出了多通道GNN通过从不同视角(补全和修剪视角)编码图学习面向对齐的嵌入,这样对结构的差异更鲁棒。
2)同时执行KG推理和对齐,这样KG间的异质性能通过补全得到显示的调节,通过跨KG 的注意力得到修剪。
3)在5个数据集上的扩展实验中得到了很好的效果。
2先验知识和框架
规则知识:规则知识![]() 可从KG中诱导出来,比如
可从KG中诱导出来,比如![]()
![]() 说明两个实体如果通过
说明两个实体如果通过![]() 连接,则它们可能也有关系
连接,则它们可能也有关系![]() ,箭头的左边是前提,右边是结论。含有p个前提一个结论的规则记为
,箭头的左边是前提,右边是结论。含有p个前提一个结论的规则记为![]()
![]()
规则证据:指的是找到满足规则中定义的前提-结论关系的合适的三元组。对于规则 k,将它的其中一个证据记做![]() ,它包含p+1个三元组,这些三元组满足
,它包含p+1个三元组,这些三元组满足![]()
![]()
实体对齐:输入两个异质KG,目标是找到尽可能多的对齐![]()
![]() ,通常我们可以很容易得到一些种子实体对和种子关系对。
,通常我们可以很容易得到一些种子实体对和种子关系对。
MuGNN框架:它的目的是学习面向实体对齐的KG嵌入。先引入KG规则推理和规则转移以显式地补全KG,利用不同的关系权重模式:KG自注意力和跨KG的注意力,来鲁棒地编码KG。框架主要由两个步骤,如下图所示:
KG补全:通过补全缺失的关系来调节结构的差异。它不仅通过规则挖掘器AMIE+诱导出规则,还基于KG间的种子对齐关系在不同的KG中转换规则。规则转移是基于这一假设:知识可以泛化到不同的KG,不管KG是何种语言或什么领域。
多通道的图神经网络:通过不同的通道编码每个KG,这些通道从不同视角(面向补全和面向修剪)来加强实体嵌入。MuGNN包含三个主要组件:1)关系加权,根据两种模式(KG自注意力和跨KG的注意力)为每个KG生成关系权重,每个类型的注意力对应一个GNN通道,这些通道在两个KG中共享参数以实现结构知识的转移;2)GNN编码器,建模整个图的特征,通过实体的邻居提高实体的嵌入,这样种子对齐信息就传播到整个图中。通过池化技术结合不同GNN编码器的输出:3)对齐模型,通过将种子实体(或关系)的嵌入push到一起将两个KG嵌入到同一向量空间。
下面是对每个步骤的详细说明
3 KG补全:这一部分介绍如何利用规则显式地补全KG。首先从每个KG中推理出规则,然后基于知识不变量的假设在KG中转移这些知识,最后在每个KG中找规则的证据。
3.1规则推理和转移
用一个比较成熟的规则挖掘系统从大规模的KG中找出霍尔规则。给定两个知识图谱,G和G’,首先分别从一个KG中挖掘规则,得到两个规则集合。两个KG中的规则知识大不相同,因为不同的KG的构建需求不同,除了用各自的规则集补充各自KG外,还在两个KG中进行规则的迁移。给定对齐的关系集合![]() 和规则
和规则![]() ,将规则
,将规则![]()
![]() 中的关系替换为其对应关系。这样就得到了一个新的规则
中的关系替换为其对应关系。这样就得到了一个新的规则![]() ,如果这一新的规则不存在,则将其加入规则集中,即
,如果这一新的规则不存在,则将其加入规则集中,即![]() ,注意当对齐关系集为空时,我们将得不到任何转移规则。
,注意当对齐关系集为空时,我们将得不到任何转移规则。
3.2 规则落地
对规则集中的规则在各自的KG中进行实例化后用于知识补全,补全后的KG不仅增加了知识的稠密性,更利于对齐模型中的知识传播,也增加了更多的约束,帮助学习质量更好的嵌入。
对于知识图谱G,给定规则k,收集可以作为其证据中前提的三元组,把所有的不在KG中的结论三元组加入到KG中,即![]() ,
,![]() ,如图1所示,我们可以从KG2中得到规则
,如图1所示,我们可以从KG2中得到规则![]() ,然后根据对齐的关系‘province’和‘dialect’将这一规则转移到KG1上,在KG1中,我们找到合适的三元组
,然后根据对齐的关系‘province’和‘dialect’将这一规则转移到KG1上,在KG1中,我们找到合适的三元组![]()
![]() ,这些三元组做为前提,能找到结论三元组
,这些三元组做为前提,能找到结论三元组![]()
![]() 。
。
注意,抽取到的规则并不是在所有情况下都成立,可以度量每个证据的置信度(未来工作)。
4 多通道的图神经网络
介绍MuGNN中涉及的三个主要组件:关系权重、多通道GNN编码器、对齐模型,来编码不同的图,学习面向对齐的嵌入。
关系加权:基于图G的结构特征得到加权的邻接矩阵,每个元素表示两个实体间的加权的关系权重。在KG中有两种类型的结构差异:由KG的天然不完全性造成的链接的缺失,和由不同的构建需求造成的实体的多余。利用两个通道编码的GNN编码每个KG,每个通道负责调解一种类型的结构差异性。也就是为每个KG生成两个邻接矩阵:基于自注意力的A1和基于跨KG注意力的A2.
KG自注意力:目的是根据KG的自身结构充分利用对齐的种子。根据当前的实体选择信息量高的邻居并为之设置高权重。类似于GAT,A1中的元素定义为
其中![]() 指加上自循环的
指加上自循环的![]() 的邻居,
的邻居,![]() 是度量邻居的重要性的注意力系数,计算方式如下:
是度量邻居的重要性的注意力系数,计算方式如下:
其中 || 表示向量连接,W和p是可训练的参数。
跨KG的注意力:目的是建模两个KG的公共子图做为结构特征以建模一致性。它能通过为没有对应关系的关系设置较低的权重来修剪掉多余的实体。A2中的元素定义如下:
其中1(.)表示如果存在就为1,不存在就为0. sim(.)是关系类型间的相似性度量,定义为关系的内积。这样A2就能找到两个KG中的最佳匹配,如果对于多余的实体,就没有这样的关系,那么权重就是0.
4.2 多通道的GNN编码器
GNN是处理图结构数据的一种神经网络模型,主要思想类似于传播模型:根据邻居节点来增强节点自身的特征。可以堆叠L层GNN以得到更远的传播。GNN的一个变体是基于谱图的图卷积网络,如GCN,每个GCN编码器以节点表示的隐含状态做为输入,并计算出新的节点表示:
其中A是邻接矩阵,H是当前的节点表示,W是可学习的参数,激活函数选择的是ReLU。受多头注意力的启发,本文利用上述提到的策略来计算邻接矩阵以从不同方面来传播信息。最后用池化方程对它们进行聚合,本文的多通道GNN编码器,通过堆叠多个GNN编码器来构建。
其中,c是通道的个数,![]() 是通道 i 中的邻接矩阵,
是通道 i 中的邻接矩阵,![]() 是第l+1层中第 i 个通道的输出的隐层状态,计算方式如下:
是第l+1层中第 i 个通道的输出的隐层状态,计算方式如下:
其中![]() 是第 i 个通道的加权参数。这里
是第 i 个通道的加权参数。这里![]() 指的是上面提到的两个注意力模式,令
指的是上面提到的两个注意力模式,令![]() 表示随机初始化的实体嵌入。这里的池化选用平均池化。
表示随机初始化的实体嵌入。这里的池化选用平均池化。
用这样的多通道GNN编码器编码每个人KG,得到![]() 表示增强的实体嵌入,其中每个通道中的参数在两个KG中是共享的。
表示增强的实体嵌入,其中每个通道中的参数在两个KG中是共享的。
4.3对齐模型
通过将种子对中的实体push到一起来将两个KG嵌入到一个统一的向量空间中。通过实体(或关系)间的距离来度量其相似度。对齐模型的目标函数是
规则知识约束
由于通过添加了由规则得到的新三元组,这样改变了KG的结构,但为了保证在嵌入空间中规则的有效性,还引入了三元组损失。以G为例,定义如下的损失函数:
其中,g是规则证据![]() 的缩写,
的缩写,![]() 和
和![]() 指所有的规则证据以及所有的三元组,
指所有的规则证据以及所有的三元组,![]() 和
和![]() 是负样本集合。
是负样本集合。![]() 对于三元组来说是三元组t的真值,计算方法为:
对于三元组来说是三元组t的真值,计算方法为:
对于证据![]() 来说计算如下:
来说计算如下:
其中,d是嵌入的维度,同理可得出另一个KG的损失。这样,多通道GNN的整体损失为:
5 实验部分
在DBP15K与DWY100K上进行实验,对于种子关系对,用DBpedia上的官方公布的数据,对于DWY-YG,由于其关系数量小,手动对齐关系。数据统计如下:
对于每个数据集,用AMIE+进行规则挖掘,得到的规则数量统计如表2所示
实验分析部分包括:总体表现,消融实验,种子实体对数量的影响,定性分析
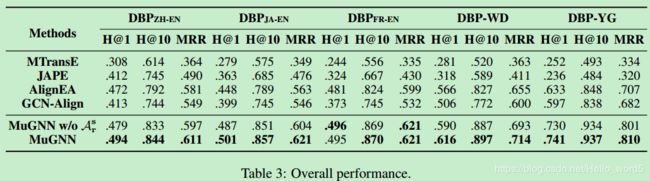
总体表现如表3所示
个人总结:感觉这个方法的亮点在于跨KG的注意力,能去掉一些对对齐来说没用的实体。