4.3 数值微分 和4.4梯度

本章讲解了导数、梯度。由于这些都是很基础的数学概念，所以本篇博客重点在于Python代码实现，而忽视概念。

1. 导数
   利用微小的差分求导数的过程称为数值微分。而基于数学式的推导求导数的过程，则称为“解析性求解”或者“解析性求导”（比如$y=x^2$，则dy/dx=2x，通过这个公式求导得到的是“真的导数”，这个过程叫做“解析性求导”）。
   代码中，参数f是一个函数，x是自变量。
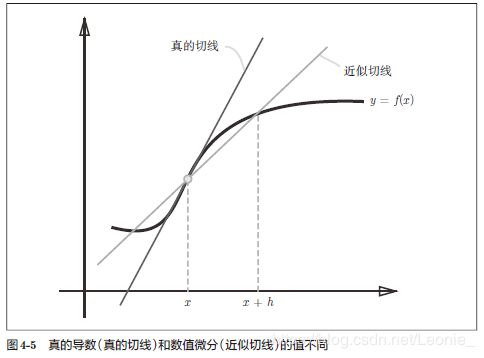
   使用中心差分【f在（x+h）与（x-h）之间的差分】的原因：因为能够减小与实际导数的误差值。（x+h）与x之间的差分称为前向差分，它与实际值的误差更大（如图4-5）

def numerical_diff(f,x):
	h=1e-4 #微小值h取0.0001 ，不能取太小，因为32位浮点数表达不了过小的值（比如1e-50）
	return (f(x+h)-f(x-h))/(2*h)#使用中心差分，能够减小与实际导数的误差值。

2. 偏导数-梯度
由全部变量的偏导数汇总而成的向量称为梯度（gradient）

def numerical_gradient(f,x):#f是函数，x是Numpy数组，该函数对数字x的各个元素求数值微分
	h=1e-4
	grad=np.zeros_like(x) #生成一个和x形状相同、元素全都为0的数组

	for idx in range(x.size):
		tmp_val=x[idx]
		x[idx]=tem_val+h
		fxh1=f(x)

		x[idx]=tmp_val-h
		fxh2=f(x)

		grad[idx]=(fxh1-fxh2)/(2*h)
		x[idx]=tmp_val
		
	return grad

梯度是一个向量，指向各点处的函数值减小最多的方向，因此无法保证梯度所指向的方向就是函数的最小值或者真正应该前进的方向。梯度法：函数的取值从当前位置沿着梯度方向前进一定距离，然后在新的地方重新求梯度，再沿着新梯度方向前进，如此反复，不断地沿梯度方向前进。寻找最小值的梯度法：梯度下降法。寻找最大值的梯度法：梯度上升法。
用数学公式表示梯度法：

或者向量形式的：$(x_0,x_1)=（x_0,x_1）-\eta (\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial x_1})$
其中$\eta$是学习率（learning rate）
使用Python实现梯度下降法：

def gradient_descent(f,init_x,lr=0.01,step_num=100):#f是需要最优化的函数，initx是初始值，lr是学习率，一般设为0.01或0.001，step_num是迭代次数
	x=init_x

	for i in range(step_num):
		grad = numerical_gradient(f,x)
		x- =lr*grad
return x

学习率过大或者过小都不好，过大的话，结果会发散成一个很大的值，过小的话，基本上没怎么更新x就结束了。学习率属于超参数，超参数不同于神经网络的参数（权重和偏置，是通过训练数据和学习算法自动获得的），超参数需要人为设定。

下一篇讲利用“损失函数”“mini-batch”梯度““梯度下降法”实现神经网络