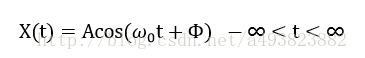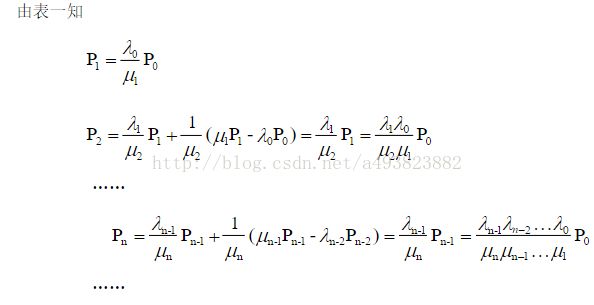排队论简介
一、随机过程(Stochastic Process):
1.定义:
设随机实验的样本空间S={s},如果对于每个s,有对应属于参数集T的参数t的函数X(s,t),那么对于所有的s,得到一组t的函数{X(s,t),t∈T},这个t的函数族称为随机过程,简记为X(s,t)或X(t)。
族中的每个函数称为该过程的一个样本,它是随机过程一次试验的物理实现,是一个确知的时间函数,称为样本函数或样本曲线。
若固定某个观察时刻t,此时X(s,t)是一个取决s的随机变量,称为在t时刻的状态。
2.举例:
给出如下随机过程的三个样本函数:
其中A与w0是正常数,而φ服从在[0,2π]上的均匀分布:
二、马尔科夫过程与生灭过程:
1.马尔科夫过程(Markov Process)与马尔科夫链:
当已知随机过程在时刻ti所处状态的条件下,过程在时刻t(>ti)所处的状态与过程在时刻ti以前的状态无关,而仅与过程在ti所处的状态有关,则称该过程为马尔科夫过程。这种特性称为随机过程的“无后效性”或马尔科夫性。
马尔科夫过程是随机过程的一个子类,其按状态空间G和参数集T是连续还是离散,可分为四类,其中有两种:
T和G都取连续集时,称为马尔科夫过程;
T和G都取离散集时,称为马尔科夫链;
2.生灭过程(Birth and death process):
离散时间的生灭过程:是每一次状态转移都发生在相邻状态之间的齐次马氏链。其状态转移矩阵P是一个夹层的矩阵,对于|i-j|>1有pij=0。
连续时间的生灭过程:一个连续时间,状态空间S={0,1,2...},为可数集的齐次马尔科夫过程{X(t),T>=0},称为连续时间生灭过程。
(可数集:每个元素能与自然数集N的每个元素之间能建立一一对应的集合)
生灭过程是用来处理输入为最简单流(即泊松分布),服务时间为负指数分布这样一类最简单排队模型的方法。
λn——系统处于瞬时状态N(t)时单位时间内顾客的平均到达率
μn——系统处于瞬时状态N(t)时单位时间内顾客的平均离去率(或服务率)
以下为一生灭过程的举例及其推导,其有无限个状态:
三、排队论简述
什么是排队论:
排队论(queueing theory)是专门研究带有随机因素产生拥挤现象的优化理论,是有关于服务设施与被服务者构成的排队服务系统的理论。
亦称随机服务系统理论。因为被服务者到达系统的时间是不确定的。
排队论是计算机通信网络和计算机系统中通信信息量研究的基础理论,信息系统通信问题的定量研究往往要求借助于排队论才能得到解决。
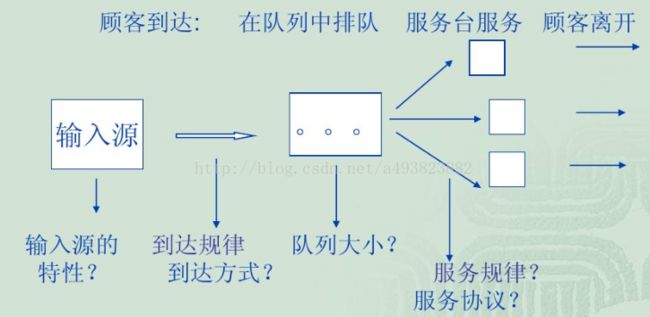
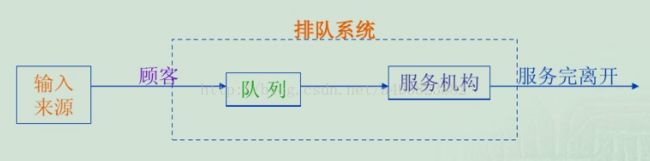
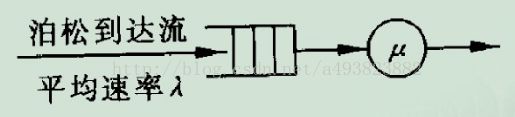
典型排队系统模型:
排队系统的三个基本组成:
输入过程:顾客按照怎样的规律到达;
排队规则:顾客按照什么样的规则排队等待服务;
服务规则:服务机构的设置,服务台的数量,服务的方式,服务时间的分布等。
(1)输入过程:
顾客到达的方式通常是一个给一个到达的,也可能是成批的。顾客到达总是有一定规律,即到达的过程或到达时间间隔符合一定的分布,称到达分布。
顾客到达或到达时间通常假定为相互独立的且遵从同一分布的随机变量。
- 顾客来源:有限/无限
- 顾客数量:有限/无限
- 经常性的顾客来源:顾客到达间隔时间服从某一概率分布
- 顾客的行为假定:在未服务之前不会离开、当看到队列很长的时候离开、从一个队列移到另一个队列
- 队列容量:有限/无限
- 排队方式:单队列、并联式多队列、串联式多队列、杂乱队列
- 服务台数量:单服务台、多服务台、无限服务台
- 服务协议:FCFS、LCFS、RSS、PR、PS、IS
- 服务时间分布:指数、常熟、k阶爱尔朗分布
(a)先来先服务:FCFS(First-Come-First-Served)
(b)后来后服务:LCFS(Last-Come-First-Served)队列是一种堆栈形式,如果队列中有两个以上等待的顾客,则把最后到达的顾客作为下一个服务对象。
(c)随机服务系统:RSS(Random Service System)在服务时从等待顾客中随意抽取一个进行服务。
(d)优先服务和动态优先服务:PR(Priority Service)预先规定优先顺序位的类别,且给到达顾客规定优先顺序位作为标记的优先权。通常按照FCFS服务,优先权分为三类:排队优先权、中断优先权、动态优先权。如计算机中断的优先级。
(e)处理器共享:PS(Processor Sharing)服务台的处理能力被平均分配给队列中的所有顾客,没有排队现象出现,当顾客的数量增加时,只是顾客的服务时间边长。如:网络服务系统。
(f)无限服务台:IS(Infinite Server)在这种情况下,队列中的每个顾客接收完全相同的服务,而且就好像它是唯一的一个顾客一样。好像对于每个顾客都可以“克隆”出一个心得服务台,而且克隆的数目可以无限。
1.排队系统的到达和服务
到达规律的描述
(1)主要描述参数
(a)到达时间:将某一时刻设为t0,顾客一次到达的时刻用..<=t-1<=t0<=t1<=t2<=...表示,若果在时刻tk到达的顾客为Nk,则到达的时点可用(tk,Nk)表示。
(b)平均到达间隔:一个顾客到达时刻之间的时宽为到达间隔。
(c)到达速率:单位时间到达顾客的平均数。
(2)到达规律:顾客到达的规律可用概率来描述,当前到达的顾客数的常见分布是泊松分布。
服务规律的描述
(1)主要描述参数
(a)平均服务时间:设服务时间的分布函数为F(t),则服务时间的平均表示为∫F(t)dt。
(b)服务速率μ:指平均服务速率,单位时间内被服务完的顾客数,即平均服务时间的倒数,μ=1/∫F(t)dt;
(2)服务规律:即服务时间的分布,典型的有指数分布、爱尔郎分布、一般分布。
2.经典排队模型
其格式为: A/B/n/S/Z
A:顾客到达的规律;B:服务时间分布;n:服务台数目;S:队列容量的大小;Z:服务规程
若队列容量大小为∞时,可简化为A/B/n/Z
若还为先来先服务时,可简化为A/B/n
其中A、B的分布可用以下字母表示:
M(Markov):若描述到达(A),则表示泊松到达;若描述服务(B),则指具有指数分布的时间。
G(General):一般分布。
Ek(Erlang):表示到达间隔或服务间隔服从k阶爱尔朗分布
还有D:定长分布(常数间隔)、H:超几何分布、L:H项式分布
典型的Z有:FCFS、LCFS、PR、RSS
3.基本排队关系
由利特尔法则(Little's Law),有以下公式:
(1)Lq=λWq
Wq是一个顾客平均排队等待的时间,λ是顾客平均到达率,所以在Wq时间内有λWq个顾客到达,Lq表示排队等待服务的平均顾客数量,故Lq=λWq。
(2)L=λW
系统中的平均顾客数(L)(包括等待的和正在被服务的顾客)等于顾客的平均到达率(λ)乘以一个顾客在系统中花费的平均时间(W)。
(3)W=Wq+1/μ
一个顾客在系统中花费的时间(W),就是它等待的时间(Wq)加上被服务的时间(1/μ)。
4.队列分析的任务
队列分析的基本任务是:
给出如下输入信息(概率分布):
到达速率(λ)、服务时间(1/μ)
求出如下输出信息(均值、标准差):
等待顾客的数量(Lq)、等待时间(Wq)、系统中顾客的数量(L)、逗留时间(W)
四、几个常用的排队模型
1.排队模型与生灭过程:
※如果用N(t)表示时刻t系统中的顾客数,则{N(t),t>=0}就构成了一个随机过程。如果用“生”表示顾客的到达,“灭”表示顾客的离去,则对许多排队过程来说,{N(t),t>=0}是一类特殊的随机过程——生灭过程。
※服务台忙的时间比率(服务强度):顾客到达速率/服务速率,即ρ=λ/μ.
2.M/M/1模型
(1)生灭过程模型:
为 "二、2.生灭过程”中的模型。
根据连续生灭过程稳定的条件,要求ρ<1。有如下推导:
Pk表示在系统稳定状态下,有k个顾客的概率。
其为服从参数为(1-ρ)的改进型几何分布,根据几何型分布可得其数字特征,即顾客数量的均值与方差:
均值L=E=ρ/(1-ρ),方差D=ρ/(1-ρ)2
根据little定理,顾客平均花费时间W=L/λ=1/(μ(1-ρ))
因为W=Wq+1/μ,Wq=W-1/μ=ρ/(μ(1-ρ))
由little定理,Lq=λWq=ρ2/(1-ρ)
(2)M/M/1系统运行指标:
※系统中平均顾客数:L=ρ/(1-ρ)
※顾客在系统中平均等待时间:W=1/(μ(1-ρ))
※队列中平均顾客数:Lq=ρ2/(1-ρ)
※顾客在队列中平均等待时间:Wq=ρ/(μ(1-ρ))
(3)例题(均为M/M/1系统):
①一条通信线路的带宽是2000bps,该线路用来传一个字符(8位bit),来自应用的要求是12000字符/分
求:等待被传输的平均字符数Lq与每个字符平均传输时间W。
解:设单位时间为秒,则μ=2000/8=250,λ=12000/60=200,则ρ=0.8
Lq=0.64/0.2=3.2,W=0.8/(250*0.2)=16ms
②一个书店平均每分钟有3个顾客到达,正常情况有48个顾客在书店中,求每一个顾客在商店花费的平均时间。
解:设单位时间为分钟,易知λ=3;因为L=48,得ρ=48/49,所以μ=49/16,;所以Wq=(48/49)/((49/16)*(1/49))≈15.6分
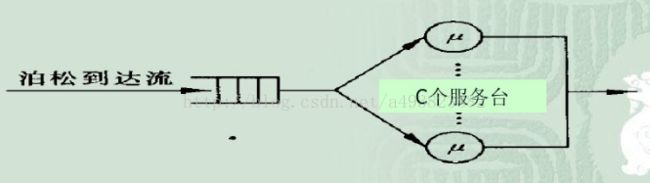
3.M/M/c 队列模型:
该队列系统的顾客到达为泊松流,到达速率为λ,有并列的c个服务台,每个服务台的服务速率为μ,服务规则FCFS。所有服务台共享一个公用的队列。
由于每个服务台工作是相互独立的(无协作)且平均服务率相同,于是整服务系统的平均服务率为cμ(n>=c)或nμ(n
(1)生灭过程模型:
平衡条件:ρ=λ/cμ<1
有如下推导:
(2)运行指标
(3)例题(服从M/M/c)M/M/1与M/M/c的比较:
某银行有3个出纳员,每人平均每小时可服务12人,顾客的到达服从泊松分布,平均每小时到达30个人。求:
①三名出纳员都忙的概率及该银行的主要运行指标;
②若所有的顾客排成3队,平均分摊到达人数(每队每小时到达10人),计算主要运行指标;
③对比①②,得出什么结论?
解: