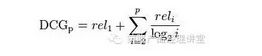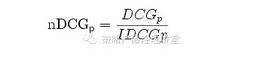【方法】搜索排序评估方法
在策略相关的产品如搜索、排序、推荐等功能的评估中,除了一般性数据分析方法之外,还有有一些特有的且相对比较固定的评估工具,这些评估工具都取之于信息检索科学的常用评估方法。要了解这些首先要了解策略产品的效果评估,我们必须要引入一些必要的信息检索相关的知识。
1.召回率和准确率
信息检索领域两个最基本指标是召回率(Recall Rate)和准确率(Precision Rate),召回率也叫查全率,准确率也叫查准率,概念公式:
召回率(Recall)=检索到的相关内容 / 所有相关的内容总数
准确率(Precision)=检索到的相关内容 / 所有检索到的内容总数
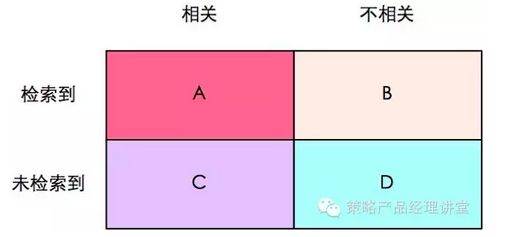
为了直观的描述这两个概念,我们用是否相关和是否被检索到两个维度的指标来对每一次信息检索之后的内容分类。是否相关指内容和检索条件是不是相关,如检索“酒店”,系统中所有的酒店内容就是相关,而“美食”的内容就是不相关的,一般情况下,相关的内容就是理论上需要完全被检索到的内容,这个数值和检索的策略或算法没有关系。是否被检索到是针对检索结果的描述指标,检索完成后我们才能对系统内容做是否被检索到的区分,这个数值和检索策略或算法相关。通过是否相关和是否被检索到两个维度的指标,我们可以将检索完成后的内容分为四类,如下图:
联系图表,召回率就是检索到的相关内容(A)在所有相关内容中的比例(A+C),而准确率就是检索到的相关内容(A)在所有检索到的内容(A+B)中的比例。
但是如何算图1中的A、B、C、D呢?一般,这需要人工标注,人工标注数据需要较多时间且枯燥,如果仅仅是做实验可以用已知的场景来测试,比如我们已知搜索“A酒店”应该出的搜索结果,那么我们就可以通过不同策略在搜索“A酒店”的表现来计算不同策略的A、B、C、D值,这种方式简便易行,能够针对性的解决问题,但是只能解决已知的问题。当然,还有一个办法,找个一个比较成熟的算法作为基准,用该算法的结果作为样本来进行比照,当然这个方法也有点问题,那就是我们无法得知天花板在哪里,也就是无法预知最佳效果如何。
在实际项目中,我们单方面追求准确率和召回率都是不对的。准确率和召回率是互相影响的,理想情况下肯定是做到两者都高,但是一般情况下准确率高、召回率就低;召回率低、准确率高。如果是做搜索,那就是保证一定召回的情况下提升准确率;如果做反垃圾、反作弊,则是保证一定准确率的条件下,提升召回率。
2.F值
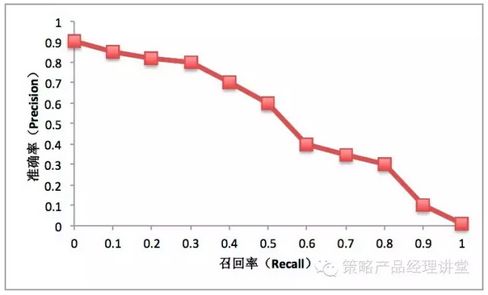
一般情况,对同一个策略模型,用不同的阀值,可以统计出一组不同阀值下的精确率和召回率关系,我们称之为P-R曲线,如下图:
图中横坐标是召回率,用R(Recall)表示;纵坐标是准确率,用P(Precision)表示。有时候,我们在P和R做出平衡,因此我们需要用一个值来体现策略在P值和R值两方面的整体表现。最普通也最容易理解的是F1值,F1值的计算公式如下:
F 1= 2 * P * R / (P + R)
更通用的公式是F=(1+β^2)*P*R/(β^2*P+R)
用F1值来体现准确率和召回率的综合表现非常直观且易于理解,但是也有一个明显的缺陷,F1值的计算中,P和R的权重是一样的,也就是对召回和准确的要求是一样。在大多数情况下,我们在召回率和准确率上有不同的要求,因而我们也常用F2和F0.5来评价策略的效果,F2 = 5P * R / (4P + R),表示更重视召回率,F0.5(F2 = 1.25P * R / (0.25P + R),表示更重视准确率。
3.ROC和AUC
前面给大家介绍了F值,细究不难发现,它只能表示单点的效果而无法表示策略的整理效果,下面介绍的内容,将是一些能评估策略整体效果的评估方法。
ROC的全名叫做Receiver Operating Characteristic,是评价分类器(需要说明)的指标,一般分类识别相关的策略我们使用ROC值来评价。我们用上面第一个图的方式来说明这个值,我们将ABCD稍作变换如下图:
正确正例(True Positive,TP)表示将正例(预测)分为正例的内容;错误正例(False Positive,FP)表示将负例分为正例的内容;错误反例(False Negtive,FN)将正例分为负例的内容;正确负例(True Negtive,TN)表示将负例分为负例的内容。其中,ROC关注两个指标:
正确正例比例True Positive Rate ( TPR ) = TP / [ TP + FN] ,TPR代表能将正例分对的概率
错误正例比例False Positive Rate( FPR ) = FP / [ FP + TN] ,FPR代表将负例错分为正例的概率
ROC的主要分析方法是一个画在ROC空间的曲线(ROC curve):在ROC 空间中,每个点的横坐标是FPR,纵坐标是TPR,这也就描绘了分类器在TP(真正的正例)和FP(错误的正例)间的平衡关系。我们知道,对于二值分类问题,实例的预测值往往是连续值,我们通过设定一个阈值,将实例分类到正类或者负类。比如我们通过数据挖掘计算酒店不接待客户的预测值是一个0-1的分布,然后设定一个阈值0.5,如果大于0.5,我们则认为酒店存在不接待用户的情况。因此我们可以变化阈值,根据不同的阈值进行分类,然后根据分类结果计算的TPR值和FPR值得到ROC空间中相应的点,连接这些点就形成ROC曲线。ROC曲线会经过(0,0)(1,1)两个点,实际上(0, 0)和(1, 1)连线形成的ROC曲线代表的是一个随机分类器。一般情况下,这个曲线都应该处于(0, 0)和(1, 1)连线的上方,否则,分类器的策略就是有问题的。
用ROC curve来表示分类器的效果很直观好用,也能够观测在不同TPR和FPR下分类策略的表现。但是,我们仍然希望能够用一个特定的值来表示分类器策略的好坏,于是Area Under roc Curve(AUC)就出现了。顾名思义,AUC的值就是处于ROC曲线下方的那部分面积的大小。
可以预见的是,AUC的值介于0.5(随机分类器的AUC值)到1.0之间,通常情况下,我们认为较大的AUC代表了较好的效果。
4.Prec@k和MAP(Mean Average Precision@K)
MAP也是评估检索策略效果的方式之一,与AUC不同的是,除了考虑召回结果的整体准确率之外,MAP也考量召回结果条目的顺序。MAP是Mean Average Precision@K的缩写,要了解MAP,我们需要逐步了解Prec@K和AP@K的概念。
Prec@K表示设定一个阈值K,在检索结果到第K个正确召回为止,排序结果的相关度。假设某次的检索结果如下:
注:绿色表示搜索结果与搜索词相关,红色表示不相关。
在这个案例中Prec@1=1、Prec@3=2/3、Prec@5=3/5。也许你已经发现了,Prec@K也只能表示单点的策略效果,为了体现策略的整体效果,我们需要使用AP@K。
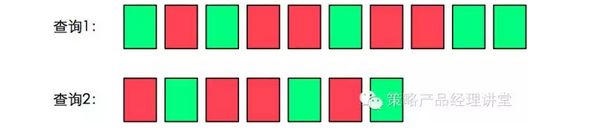
Average Precision@K是指到第K个正确的召回为止,从第一个正确召回到第K个正确召回的平均正确率。下面我们用两个排序案例来理解AP@K。假设存在以下两个排序,我们直观的理解,结果1是优于结果2的,那么这种优劣会如何体现在AP@K值中呢?
对于结果1,AP@K=(1.0+0.67+0.75+0.8+0.83+0.6)/6=0.78,对于结果2,AP@K=(0.5+0.4+0.5+0.57+0.56+0.6)/6=0.52,可以看到,效果优的排序结果的AP@K值大于效果劣的那一组。
对于一次查询,AP@K值可以判断优劣,但是如果涉及到一个策略在多次查询的效果,我们需要引入另一个概念MAP@K(Mean Average Precision@K),简单的说,MAP@K的计算的是搜索查询结果AP@K值的均值。假设某个策略在两个不同查询下的输出结果如下:
在以上案例中,查询1的AP@K=(1.0+0.67+0.5+0.44+0.5)/5=0.62,查询的2的AP@K=(0.5+0.4+0.43)/3=0.44,则我们计算这个策略的MAP@K=(0.62+0.44)/2=0.53。对使用MAP@K进行评估的系统,我们认为MAP@K值较高的策略效果更好。
5.CG、DCG和nDCG
搜索引擎一般采用PI(per item)的方式进行评测。简单地说就是逐条对搜索结果进行分等级的打分,回顾MAP指标,我们对每个条目的值是的评价是用0或1表示,相较于MAP指标,D CG能够让我们让多值指标来评价。
在DCG指标的计算中,假设我们现在在谷歌上搜索一个词,然后得到5个结果。我们可以对这些结果进行3个等级的区分:Good(好)、Fair(一般)、Bad(差),然后赋予他们分值分别为3、2、1,假定通过逐条打分后,得到这5个结果的分值分别为3、2 、1 、3、 2。如果要我们评价这次查询的效果,可以用Cumulative Gain值来评估。
CG是在这个查询输出结果里面所有的结果的等级对应的得分的总和。如一个输出结果页面有P个结果,CG被定义为:
不难看出,CG并不考虑在搜索结果的排序信息,CG得分高只能说明这个结果页面总体的质量比较高并不能说明这个算法做的排序好或差。在上面谷歌的例子中,CG=3+2+1+3+2=11,如果调换第二个结果和第三个结果的位置CG=3+1+2+3+2=11,并没有改变总体的得分。
因此,如果我们要评估返回结果质量还要考量输出排序的话。首先,我们要说明什么是好的排序?一般来说,好的排序要把Good的结果排到Fair结果上面、Fair结果排到Bad结果上面,如果有Bad的结果排在了Good上面,那当然排序就不好了。
在一个搜索结果列表里面,比如有两个结果的打分都是Good,但是有一个是排在第1位,还有一个是排在第40位,虽然这两个结果一样都是Good,但是排在第40位的那个结果因为被用户看到的概率是比较小的,他对这整个搜索结果页面的贡献值是相对排在第一位那个结果来得小的。
为了能够完成评估排序的目的,我们需要采用DCG(Discounted Cumulative Gain)值。
DCG的思想比较容易理解,等级比较高的结果却排到了比较后面,那么在统计分数时,就应该对这个结果的得分有所打折。一个有P(P≥2)个结果的搜索结果页面的DCG定义为:
为什么要用以2为底的对数函数?这个并没有明确的科学依据,大概是根据大量的用户点击与其所点内容的位置信息,模拟出一条衰减的曲线。
那么在上面百度的例子中:DCG=3+(1+1.26+1.5+0.86)=7.62。但是DCG在评估策略效果的过程中,因为不同搜索模型给出的结果有多有少,仍然会造成无法对比两个模型的效果。为了避免这种情况,我们进一步优化这个指标,成为nDCG(normalize DCG),顾名思义,就是将一个策略的效果标准归一化,以方便不同策略的效果对比。公式如下:
公式中的iDCG(ideal DCG)就是理想的DCG。iDCG如何计算?首先要拿到搜索的结果,然后对这些结果进行排序,排到最好的状态后,算出这个排列下的DCG,就是iDCG。因此nDCG是一个0-1的值,nDCG越靠近1,说明策略效果越好,或者说只要nDCG<1,策略就存在优化调整空间。因为nDCG是一个相对比值,那么不同的搜索结果之间就可以通过比较nDCG来决定哪个排序比较好。在上面的例子中,理想的排序应该是3 、3 、2 、2 、1,那么iDCG=3+3+1.26+1+0.43=8.69,nDCG=DCG/iDCG=7.62/8.69=0.88。
以上给大家介绍一些常见的评价方式,但是这几种评估方式并不一定能覆盖所有场景,一般情况下,我们需要根据自己的需要适当的对这些评估方式做些许的改进来更加符合具体场景的要求,比如在nDCG中调整评分的层级或分数,甚至根据自身用户的特征调整衰减函数的计算方式等等。但在所有的评估改进中,一般无法忽略召回率、正确率和排序三个基本维度的效果。我们不能照搬前人成果,活学活用,才是产品经理应该做的事
原文:http://www.woshipm.com/pmd/232014.html