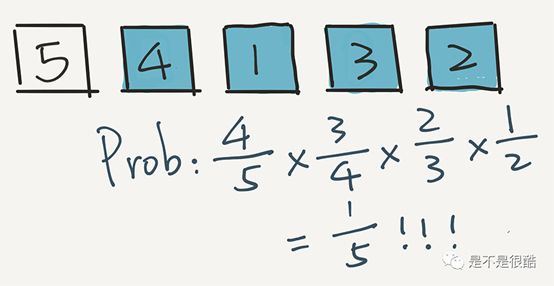首先来思考一个问题:
设计一个公平的洗牌算法
1.
看问题,洗牌,显然是一个随机算法了。随机算法还不简单?随机呗。把所有牌放到一个数组中,每次取两张牌交换位置,随机 k 次即可。
如果你的答案是这样,通常面试官会进一步问一下,k 应该取多少?100?1000?10000?
很显然,取一个固定的值不合理。如果数组中有 1000000 个元素,随机 100 次太少;如果数组中只有 10 个元素,随机 10000 次又太多。一个合理的选择是,随机次数和数组中元素大小相关。比如数组有多少个元素,我们就随机多少次。
这个答案已经好很多了。但其实,连这个问题的本质都没有触及到。此时,面试官一定会狡黠地一笑:这个算法公平吗?
我们再看问题:设计一个公平的洗牌算法。
问题来了,对于一个洗牌算法来说,什么叫“公平”?这其实是这个问题的实质,我们必须定义清楚:什么叫公平。
一旦你开始思考这个问题,才触及到了这个问题的核心。在我看来,不管你能不能最终给出正确的算法,如果你的思路是在思考对于洗牌算法来说,什么是“公平”,我都觉得很优秀。
因为背出一个算法是简单的,但是这种探求问题本源的思考角度,绝不是一日之功。别人告诉你再多次“要定义清楚问题的实质”都没用。这是一种不断面对问题,不断解决问题,逐渐磨炼出来的能力,短时间内无法培训。
这也是我经常说的,面试不是标准化考试,不一定要求你给出正确答案。面试的关键,是看每个人思考问题的能力。
说回我们的洗牌算法,什么叫公平呢?一旦你开始思考这个问题,其实答案不难想到。洗牌的结果是所有元素的一个排列。一副牌如果有 n 个元素,最终排列的可能性一共有 n! 个。公平的洗牌算法,应该能等概率地给出这 n! 个结果中的任意一个。
如思考到这一点,我们就能设计出一个简单的暴力算法了:对于 n 个元素,生成所有的 n! 个排列,然后,随机抽一个。
这个算法绝对是公平的。但问题是,复杂度太高。复杂度是多少呢?O(n!)。因为,n 个元素一共有 n! 种排列,我们求出所有 n! 种排列,至少需要 n! 的时间。
有一些同学对 O(n!) 没有概念。我本科时就闹过笑话,正儿八经地表示 O(n!) 并不是什么大不了不起的复杂度。实际上,这是一个比指数级 O(2^n) 更高的复杂度。因为 2^n 是 n 个 2 相乘;而 n! 也是 n 个数字相乘,但除了 1,其他所有数字都是大于等于 2 的。当 n>=4 开始,n! 以极快的的速度超越 2^n。
O(2^n) 已经被称为指数爆炸了。O(n!) 不可想象。
所以,这个算法确实是公平的,但是,时间不可容忍。
3.
我们再换一个角度思考“公平”这个话题。其实,我们也可以认为,公平是指,对于生成的排列,每一个元素都能等概率地出现在每一个位置。或者反过来,每一个位置都能等概率地放置每个元素。
这个定义和上面的最终洗牌结果,可以等概率地给出这 n! 个排列中的任意一个,是等价的。这个等价性,可以证明出来。并不难。如果正在学习概率论的同学,还比较习惯概率论处理问题的思想,应该能很快搞定:)
基于这个定义,我们就可以给出一个简单的算法了。说这个算法简单,是因为他的逻辑太容易了,就一个循环:
这么简单的一个算法,可以保证上面我所说的,对于生成的排列,每一个元素都能等概率的出现在每一个位置。或者反过来,每一个位置都能等概率的放置每个元素。
大家可以先简单的理解一下这个循环在做什么。其实非常简单,i 从后向前,每次随机一个 [0...i] 之间的下标,然后将 arr[i] 和这个随机的下标元素,也就是 arr[rand() % (i + 1)] 交换位置。
大家注意,由于每次是随机一个 [0...i] 之间的下标,所以,我们的计算方式是 rand() % (i + 1),要对 i + 1 取余,保证随机的索引在 [0...i] 之间。
这个算法就是大名鼎鼎的 Knuth-Shuffle,即 Knuth 洗牌算法。
这个算法的原理,我们稍后再讲。先来看看 Knuth 何许人也?
中文名:高纳德。算法理论的创始人。我们现在所使用的各种算法复杂度分析的符号,就是他发明的。上世纪 60-70 年代计算机算法的黄金时期,近乎就是他一手主导的。他的成就实在太多,有时间单独发文介绍,但是,我觉得一篇文章是不够的,一本书还差不多。
大家最津津乐道的,就是他所写的《The Art of Computer Programming》,简称 TAOCP。这套书准备写七卷本,然后,到今天还没有写完,但已经被《科学美国人》评为可以媲美相对论的巨著。
微软是 IT 界老大的年代,比尔盖茨直接说,如果你看完了这套书的第一卷本,请直接给我发简历。
至于这套书为什么写的这么慢?因为老爷子写到一半,觉得当下的文字排版工具都太烂,于是转而发明出了现在流行的LaTex文字排版系统...
另外,老爷子可能觉得当下的编程语言都不能完美地表现自己的逻辑思想,还发明了一套抽象的逻辑语言,用于这套书中的逻辑表示...
4.
是时候仔细的看一下,这个简单的算法,为什么能做到保证:对于生成的排列,每一个元素都能等概率的出现在每一个位置了。
其实,简单的吓人:)
在这里,我们模拟一下算法的执行过程,同时,对于每一步,计算一下概率值。
我们简单的只是用 5 个数字进行模拟。假设初始的时候,是按照 1,2,3,4,5 进行排列的。
那么,根据这个算法,首先会在这五个元素中选一个元素,和最后一个元素 5 交换位置。假设随机出了 2
下面,我们计算 2 出现在最后一个位置的概率是多少?非常简单,因为是从 5 个元素中选的嘛,就是 1/5。实际上,根据这一步,任意一个元素出现在最后一个位置的概率,都是 1/5。
下面,根据这个算法,我们就已经不用管 2 了,而是在前面 4 个元素中,随机一个元素,放在倒数第二的位置。假设我们随机的是 3。3 和现在倒数第二个位置的元素 4 交换位置。
下面的计算非常重要。3 出现在这个位置的概率是多少?计算方式是这样的:
其实很简单,因为 3 逃出了第一轮的筛选,概率是 4/5,但是 3 没有逃过这一轮的选择。在这一轮,一共有4个元素,所以 3 被选中的概率是 1/4。因此,最终,3 出现在这个倒数第二的位置,概率是 4/5 * 1/4 = 1/5。还是 1/5 !
实际上,用这个方法计算,任意一个元素出现在这个倒数第二位置的概率,都是 1/5。
相信聪明的同学已经了解了。我们再进行下一步,在剩下的三个元素中随机一个元素,放在中间的位置。假设我们随机的是 1。
关键是:1 出现在这个位置的概率是多少?计算方式是这样的:
即 1 首先在第一轮没被选中,概率是 4/5,在第二轮又没被选中,概率是 3/4 ,但是在第三轮被选中了,概率是 1/3。乘在一起,4/5 * 3/4 * 1/3 = 1/5。
用这个方法计算,任意一个元素出现在中间位置的概率,都是 1/5。
这个过程继续,现在,我们只剩下两个元素了,在剩下的两个元素中,随机选一个,比如是4。将4放到第二个位置。
然后,4 出现在这个位置的概率是多少?4 首先在第一轮没被选中,概率是 4/5;在第二轮又没被选中,概率是 3/4;第三轮还没选中,概率是 2/3,但是在第四轮被选中了,概率是 1/2。乘在一起,4/5 * 3/4 * 2/3 * 1/2 = 1/5。
用这个方法计算,任意一个元素出现在第二个位置的概率,都是 1/5。
最后,就剩下元素5了。它只能在第一个位置呆着了。
那么 5 留在第一个位置的概率是多少?即在前 4 轮,5 都没有选中的概率是多少?
在第一轮没被选中,概率是 4/5;在第二轮又没被选中,概率是 3/4;第三轮还没选中,概率是 2/3,在第四轮依然没有被选中,概率是 1/2。乘在一起,4/5 * 3/4 * 2/3 * 1/2 = 1/5。
你看,在整个过程中,每一个元素出现在每一个位置的概率,都是 1/5 !
所以,这个算法是公平的。
当然了,上面只是举例子。这个证明可以很容易地拓展到数组元素个数为 n 的任意数组。整个算法的复杂度是 O(n) 的。