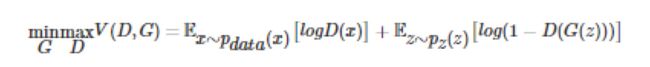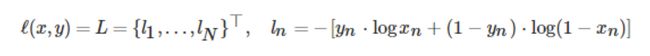DCGAN的PyTorch实现
DCGAN
1.什么是GAN
GAN是一个框架,让深度模型可以学习到数据的分布,从而通过数据的分布生成新的数据(服从同一分布)。
其由一个判别器和一个生成器构成,生成器负责生成“仿造数据”,判别器负责判断“仿造数据”的质量。两者一起进化,导致造假货和识别假货的两个模型G/D都能有超强的造假和识别假货的能力。
最终训练达到类似纳什均衡的平衡状态,就是分辨器已经分辨不出真假,其分别真假的成功率只有50%(和瞎猜没有区别)。
假设原数据分布为x(可以是一张真实图片等多维数据),判别器D(),随机变量Z,生成器为G()。D(x)生成一个标量代表x来自真实分布的概率。Z是一个随机噪声,G(Z)代表随机噪声Z(也称为隐空间向量)到真实分布P_data的映射。G(Z)的生成数据的概率分布记作P_G.
所以D(G(z))就是一个标量代表其生成图片是真实图片的概率
,同时D和G在玩一个你最小(G)我最大(D)的游戏。D想把自己分别真假图片x的成功率最大化
logD(x)
G想把造假图片z和真实图片x的差距最小化
log(1-D(G(x))。
总目标函数(loss function)可以写成:
2.什么是DCGAN
DCGAN是GAN的一个扩展,卷积网络做判别器,反卷积做生成器。
判别器通过大幅步的卷积网络、批量正则化、LeakyRelu激活函数构成。输入一个3*64 *64的图片,输出一个真假概率值。
生成器由一个反卷积网络、批量正则化、Relu激活函数构成,通过输入一个隐变量z(如标准正态分布)。同时输出一个3*64 *64的图片。
同时《 Unsupervised Representation Learning With Deep Convolutional Generative Adversarial Networks》的原作者还给出如何设置优化器(optimizers),如何计算损失函数,如何初始化模型weights等技巧。
初始导入代码如下:
from __future__ import print_function
#%matplotlib inline
import argparse
import os
import random
import torch
import torch.nn as nn
import torch.nn.parallel
import torch.backends.cudnn as cudnn
import torch.optim as optim
import torch.utils.data
import torchvision.datasets as dset
import torchvision.transforms as transforms
import torchvision.utils as vutils
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML
# Set random seed for reproducibility
manualSeed = 999
#manualSeed = random.randint(1, 10000) # use if you want new results
print("Random Seed: ", manualSeed)
random.seed(manualSeed)
torch.manual_seed(manualSeed)
3.输入设置
输入参数设置
- dataroot - the path to the root of the dataset folder. We will talk more about the dataset in the next section
- workers - the number of worker threads for loading the data with the DataLoader
- batch_size - the batch size used in training. The DCGAN paper uses a batch size of 128
- image_size - the spatial size of the images used for training. This implementation defaults to 64x64. If another size is desired, the structures of D and G must be changed.
- nc - number of color channels in the input images. For color images this is 3
- nz - length of latent vector
- ngf - relates to the depth of feature maps carried through the generator
- ndf - sets the depth of feature maps propagated through the discriminator
- num_epochs - number of training epochs to run. Training for longer will probably lead to better results but will also take much longer
- lr - learning rate for training. As described in the DCGAN paper, this number should be 0.0002
- beta1 - beta1 hyperparameter for Adam optimizers. As described in paper, this number should be 0.5
- ngpu - number of GPUs available. If this is 0, code will run in CPU mode. If this number is greater than 0 it will run on that number of GPUs
# Root directory for dataset
dataroot = "data/celeba"
# Number of workers for dataloader
workers = 2
# Batch size during training
batch_size = 128
# Spatial size of training images. All images will be resized to this
# size using a transformer.
image_size = 64
# Number of channels in the training images. For color images this is 3
nc = 3
# Size of z latent vector (i.e. size of generator input)
nz = 100
# Size of feature maps in generator
ngf = 64
# Size of feature maps in discriminator
ndf = 64
# Number of training epochs
num_epochs = 5
# Learning rate for optimizers
lr = 0.0002
# Beta1 hyperparam for Adam optimizers
beta1 = 0.5
# Number of GPUs available. Use 0 for CPU mode.
ngpu = 1
4.数据
数据集用的是港中文的Celeb-A
# We can use an image folder dataset the way we have it setup.
# Create the dataset
dataset = dset.ImageFolder(root=dataroot,
transform=transforms.Compose([
transforms.Resize(image_size),
transforms.CenterCrop(image_size),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
]))
# Create the dataloader
dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size,
shuffle=True, num_workers=workers)
# Decide which device we want to run on
device = torch.device("cuda:0" if (torch.cuda.is_available() and ngpu > 0) else "cpu")
# Plot some training images
real_batch = next(iter(dataloader))
#real_batch是一个列表
#第一个元素real_batch[0]是[128,3,64,64]的tensor,就是标准的一个batch的4D结构:128张图,3个通道,64长,64宽
#第二个元素real_batch[1]是第一个元素的标签,有128个label值全为0
plt.figure(figsize=(8,8))
plt.axis("off")
plt.title("Training Images")
plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(device)[:64], padding=2, normalize=True).cpu(),(1,2,0)))
#这个函数能让图片显示
#plt.show()
5.实现(Implementation)
5.1 参数初始化(Weight Initialization)
w初始化为均值为0,标准差为0.02的正态分布
# custom weights initialization called on netG and netD
def weights_init(m):
classname = m.__class__.__name__
if classname.find('Conv') != -1:
nn.init.normal_(m.weight.data, 0.0, 0.02)
elif classname.find('BatchNorm') != -1:
nn.init.normal_(m.weight.data, 1.0, 0.02)
nn.init.constant_(m.bias.data, 0)
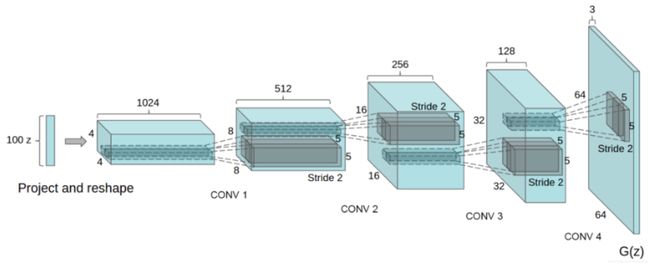
5.2 生成器(Generator)
生成器G是构造一个由向量Z(隐空间)到真实数据空间的映射(map)
-
nz=100,z输入时的长度
-
nc=3,输出时的chanel,彩色是RGB三通道
-
ngf=64,指的是生成的特征为64*64
-
反卷积的函数为:
ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1)
参数为:1.输入、2.输出、3.核函数、4.卷积核步数、5.输入边填充、6.输出边填充、7.group、8.偏置、9.膨胀
class Generator(nn.Module):
def __init__(self, ngpu):
super(Generator, self).__init__()
self.ngpu = ngpu
self.main = nn.Sequential(
# input is Z, going into a convolution
nn.ConvTranspose2d( nz, ngf * 8, 4, 1, 0, bias=False),
#输入100,输出64*8,核函数是4*4
nn.BatchNorm2d(ngf * 8),
nn.ReLU(True),
# state size. (ngf*8) x 4 x 4
nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
nn.BatchNorm2d(ngf * 4),
nn.ReLU(True),
# state size. (ngf*4) x 8 x 8
nn.ConvTranspose2d( ngf * 4, ngf * 2, 4, 2, 1, bias=False),
nn.BatchNorm2d(ngf * 2),
nn.ReLU(True),
# state size. (ngf*2) x 16 x 16
nn.ConvTranspose2d( ngf * 2, ngf, 4, 2, 1, bias=False),
nn.BatchNorm2d(ngf),
nn.ReLU(True),
# state size. (ngf) x 32 x 32
nn.ConvTranspose2d( ngf, nc, 4, 2, 1, bias=False),
nn.Tanh()
# state size. (nc) x 64 x 64
)
def forward(self, input):
return self.main(input)
实例化生成器,初始化参数w
# Create the generator
netG = Generator(ngpu).to(device)
# Handle multi-gpu if desired
if (device.type == 'cuda') and (ngpu > 1):
netG = nn.DataParallel(netG, list(range(ngpu)))
# Apply the weights_init function to randomly initialize all weights
# to mean=0, stdev=0.2.
netG.apply(weights_init)
# Print the model
print(netG)
out:
Generator(
(main): Sequential(
(0): ConvTranspose2d(100, 512, kernel_size=(4, 4), stride=(1, 1), bias=False)
(1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): ConvTranspose2d(512, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(4): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(5): ReLU(inplace=True)
(6): ConvTranspose2d(256, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(7): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(8): ReLU(inplace=True)
(9): ConvTranspose2d(128, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(10): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(11): ReLU(inplace=True)
(12): ConvTranspose2d(64, 3, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(13): Tanh()
)
)
5.3 判别器(Discriminator)
判别器D是一个二元分类器,判别输入的图片真假。通过输入图片进入一连串的卷积层中,经过卷积(Strided Convolution)、批量正则(BatchNorm)、LeakyReLu激活,最终通过Sigmoid激活函数输出一个概率选择。
以上的结构如有必要可以扩展更多的层,不过DCGAN的设计者通过实验发现调整步幅的卷积层比池化的下采样效果要好,因为通过卷积网络可以学习到自己的池化函数。同时批量正则化和leakly relu函数都可以提高梯度下降的质量,这些效果在同时训练G和D时显得更为突出。
class Discriminator(nn.Module):
def __init__(self, ngpu):
super(Discriminator, self).__init__()
self.ngpu = ngpu
self.main = nn.Sequential(
# input is (nc) x 64 x 64
nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
nn.LeakyReLU(0.2, inplace=True),
# state size. (ndf) x 32 x 32
nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
nn.BatchNorm2d(ndf * 2),
nn.LeakyReLU(0.2, inplace=True),
# state size. (ndf*2) x 16 x 16
nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
nn.BatchNorm2d(ndf * 4),
nn.LeakyReLU(0.2, inplace=True),
# state size. (ndf*4) x 8 x 8
nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
nn.BatchNorm2d(ndf * 8),
nn.LeakyReLU(0.2, inplace=True),
# state size. (ndf*8) x 4 x 4
nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
nn.Sigmoid()
)
def forward(self, input):
return self.main(input)
构建D,并初始化w方程,并且输出模型的结构。
# Create the Discriminator
netD = Discriminator(ngpu).to(device)
# Handle multi-gpu if desired
if (device.type == 'cuda') and (ngpu > 1):
netD = nn.DataParallel(netD, list(range(ngpu)))
# Apply the weights_init function to randomly initialize all weights
# to mean=0, stdev=0.2.
netD.apply(weights_init)
# Print the model
print(netD)
out:
Discriminator(
(main): Sequential(
(0): Conv2d(3, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(1): LeakyReLU(negative_slope=0.2, inplace=True)
(2): Conv2d(64, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(3): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(4): LeakyReLU(negative_slope=0.2, inplace=True)
(5): Conv2d(128, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(6): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(7): LeakyReLU(negative_slope=0.2, inplace=True)
(8): Conv2d(256, 512, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(9): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(10): LeakyReLU(negative_slope=0.2, inplace=True)
(11): Conv2d(512, 1, kernel_size=(4, 4), stride=(1, 1), bias=False)
(12): Sigmoid()
)
)
5.4 损失函数&优化器(loss&optimizer)
用Pytorch自带的损失函数Binary Corss Entropy(BCELoss),其定义如下:
我们定义真图片real为1,假图片fake为0。同时设置两个优化器optimizer。在本例中
都是adam优化器,其学习率是0.0002且Beta1=0.5。为了保持生成学习的过程,我们从一个高斯分布中生成一个修正的批量数据。同时在训练过程中,我们定期放入修正的噪音给生成器G以提高拟合能力。
# Initialize BCELoss function
criterion = nn.BCELoss()
# Create batch of latent vectors that we will use to visualize
# the progression of the generator
fixed_noise = torch.randn(64, nz, 1, 1, device=device)
# Establish convention for real and fake labels during training
real_label = 1
fake_label = 0
# Setup Adam optimizers for both G and D
optimizerD = optim.Adam(netD.parameters(), lr=lr, betas=(beta1, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr=lr, betas=(beta1, 0.999))
5.5 训练
训练GAN是一种艺术,用不好超参数容易造成模式崩溃。我们通过D建立不同批次图片的真假差异,以及构建生成G函数以最大化logD(G(z))。
5.5.1 判别器D
训练判别器D的目的是让D能最大化识别真假图片的概率,通过随机梯度上升(ascending its stochastic gradient SGD)更新判别器。在实践中就是最大化log(D(x))+log(1-D(G(z)))。
以上步骤分为两步实现,第一步是从训练数据集中拿出一批真实图片作为样本,通过模型D,计算其loss即损失函数log(D(x)),然后再通过反向传播计算梯度更新损失函数。
第二步是通过生成器建立一批假样本,也通过D进行前向传播得到另一半loss值。即损失函数log(1-D(G(z))的值,同时也通过反向传播更新loss,通过1个batches的迭代更新,我们称为一次D的优化(optimizer)
5.5.2 生成器G
在GAN原始版本中G的实现是通过最小化log(1-D(G(z)))以增加更好的造假能力。值得注意的是原始版本并没有提供足够的梯度更新策略,特别在早期的训练学习过程中。作为修正,我们用最大化log(D(G(z)))来替代原先的策略。其中关键名词如下:
- Loss_D
计算所以批次的真假图片的判别函数,即loss= log(D(x))+log(D(G(Z))
- Loss_G
生成图片的损失函数即log(D(G(z)))
- D(x)
输出真样本批次的为真概率,从一开始的1到理论上的拟合至0.5(即G训练好的时候)
- D(G(z))
判别输出生成图片为真的概率,从一开始的0到理论上拟合至0.5(同为G训练好的时候)
训练时间和训练整体样本的次数(epoch),和样本的大小有关,代码如下:
# Training Loop
# Lists to keep track of progress
img_list = []
G_losses = []
D_losses = []
iters = 0
print("Starting Training Loop...")
# For each epoch
for epoch in range(num_epochs):
# For each batch in the dataloader
for i, data in enumerate(dataloader, 0):
############################
# (1) Update D network: maximize log(D(x)) + log(1 - D(G(z)))
###########################
## Train with all-real batch
netD.zero_grad()
# Format batch
real_cpu = data[0].to(device)
b_size = real_cpu.size(0)
label = torch.full((b_size,), real_label, device=device)
# Forward pass real batch through D
output = netD(real_cpu).view(-1)
# Calculate loss on all-real batch
errD_real = criterion(output, label)
# Calculate gradients for D in backward pass
errD_real.backward()
D_x = output.mean().item()
## Train with all-fake batch
# Generate batch of latent vectors
noise = torch.randn(b_size, nz, 1, 1, device=device)
# Generate fake image batch with G
fake = netG(noise)
label.fill_(fake_label)
# Classify all fake batch with D
output = netD(fake.detach()).view(-1)
# Calculate D's loss on the all-fake batch
errD_fake = criterion(output, label)
# Calculate the gradients for this batch
errD_fake.backward()
D_G_z1 = output.mean().item()
# Add the gradients from the all-real and all-fake batches
errD = errD_real + errD_fake
# Update D
optimizerD.step()
############################
# (2) Update G network: maximize log(D(G(z)))
###########################
netG.zero_grad()
label.fill_(real_label) # fake labels are real for generator cost
# Since we just updated D, perform another forward pass of all-fake batch through D
output = netD(fake).view(-1)
# Calculate G's loss based on this output
errG = criterion(output, label)
# Calculate gradients for G
errG.backward()
D_G_z2 = output.mean().item()
# Update G
optimizerG.step()
# Output training stats
if i % 50 == 0:
print('[%d/%d][%d/%d]\tLoss_D: %.4f\tLoss_G: %.4f\tD(x): %.4f\tD(G(z)): %.4f / %.4f'
% (epoch, num_epochs, i, len(dataloader),
errD.item(), errG.item(), D_x, D_G_z1, D_G_z2))
# Save Losses for plotting later
G_losses.append(errG.item())
D_losses.append(errD.item())
# Check how the generator is doing by saving G's output on fixed_noise
if (iters % 500 == 0) or ((epoch == num_epochs-1) and (i == len(dataloader)-1)):
with torch.no_grad():
fake = netG(fixed_noise).detach().cpu()
img_list.append(vutils.make_grid(fake, padding=2, normalize=True))
iters += 1
out:
Starting Training Loop...
[0/5][0/1583] Loss_D: 2.0937 Loss_G: 5.2060 D(x): 0.5704 D(G(z)): 0.6680 / 0.0090
[0/5][50/1583] Loss_D: 0.1916 Loss_G: 9.5846 D(x): 0.9472 D(G(z)): 0.0364 / 0.0002
[0/5][100/1583] Loss_D: 4.0207 Loss_G: 21.2494 D(x): 0.2445 D(G(z)): 0.0000 / 0.0000
[0/5][150/1583] Loss_D: 0.5569 Loss_G: 3.1977 D(x): 0.7294 D(G(z)): 0.0974 / 0.0609
[0/5][200/1583] Loss_D: 0.2320 Loss_G: 3.3187 D(x): 0.9009 D(G(z)): 0.0805 / 0.0659
[0/5][250/1583] Loss_D: 0.7203 Loss_G: 5.9229 D(x): 0.8500 D(G(z)): 0.3485 / 0.0062
[0/5][300/1583] Loss_D: 0.6775 Loss_G: 4.0545 D(x): 0.8330 D(G(z)): 0.3379 / 0.0353
[0/5][350/1583] Loss_D: 0.7549 Loss_G: 5.9064 D(x): 0.9227 D(G(z)): 0.4109 / 0.0084
[0/5][400/1583] Loss_D: 1.0655 Loss_G: 2.5097 D(x): 0.4933 D(G(z)): 0.0269 / 0.1286
[0/5][450/1583] Loss_D: 0.6321 Loss_G: 2.7811 D(x): 0.6453 D(G(z)): 0.0610 / 0.1026
[0/5][500/1583] Loss_D: 0.5064 Loss_G: 4.1399 D(x): 0.9475 D(G(z)): 0.3009 / 0.0350
[0/5][550/1583] Loss_D: 0.3838 Loss_G: 4.0321 D(x): 0.8221 D(G(z)): 0.1218 / 0.0331
[0/5][600/1583] Loss_D: 0.5549 Loss_G: 4.6055 D(x): 0.8230 D(G(z)): 0.2049 / 0.0171
[0/5][650/1583] Loss_D: 0.2821 Loss_G: 6.8137 D(x): 0.8276 D(G(z)): 0.0164 / 0.0027
[0/5][700/1583] Loss_D: 0.6422 Loss_G: 5.0119 D(x): 0.8267 D(G(z)): 0.2827 / 0.0146
[0/5][750/1583] Loss_D: 0.4332 Loss_G: 4.3659 D(x): 0.9239 D(G(z)): 0.2307 / 0.0291
[0/5][800/1583] Loss_D: 0.5344 Loss_G: 3.4145 D(x): 0.7208 D(G(z)): 0.0891 / 0.0744
[0/5][850/1583] Loss_D: 0.8094 Loss_G: 2.9318 D(x): 0.5903 D(G(z)): 0.0602 / 0.0979
[0/5][900/1583] Loss_D: 0.1598 Loss_G: 6.4141 D(x): 0.9228 D(G(z)): 0.0630 / 0.0046
[0/5][950/1583] Loss_D: 0.5083 Loss_G: 5.5467 D(x): 0.9226 D(G(z)): 0.2916 / 0.0112
[0/5][1000/1583] Loss_D: 0.6738 Loss_G: 3.9958 D(x): 0.7622 D(G(z)): 0.2480 / 0.0410
[0/5][1050/1583] Loss_D: 0.2155 Loss_G: 3.8838 D(x): 0.9092 D(G(z)): 0.0819 / 0.0432
[0/5][1100/1583] Loss_D: 1.1708 Loss_G: 1.9610 D(x): 0.4709 D(G(z)): 0.0064 / 0.2448
[0/5][1150/1583] Loss_D: 0.7506 Loss_G: 6.9292 D(x): 0.8797 D(G(z)): 0.3728 / 0.0019
[0/5][1200/1583] Loss_D: 0.2133 Loss_G: 5.5082 D(x): 0.9436 D(G(z)): 0.1272 / 0.0102
[0/5][1250/1583] Loss_D: 0.5156 Loss_G: 3.8660 D(x): 0.8073 D(G(z)): 0.1993 / 0.0357
[0/5][1300/1583] Loss_D: 0.4848 Loss_G: 5.0770 D(x): 0.9170 D(G(z)): 0.2847 / 0.0109
[0/5][1350/1583] Loss_D: 0.6596 Loss_G: 4.7626 D(x): 0.8414 D(G(z)): 0.3232 / 0.0145
[0/5][1400/1583] Loss_D: 0.2799 Loss_G: 5.1604 D(x): 0.9154 D(G(z)): 0.1494 / 0.0156
[0/5][1450/1583] Loss_D: 0.4756 Loss_G: 2.9344 D(x): 0.8164 D(G(z)): 0.1785 / 0.0955
[0/5][1500/1583] Loss_D: 0.3904 Loss_G: 2.3755 D(x): 0.7652 D(G(z)): 0.0587 / 0.1328
[0/5][1550/1583] Loss_D: 1.2817 Loss_G: 1.2689 D(x): 0.3769 D(G(z)): 0.0221 / 0.3693
[1/5][0/1583] Loss_D: 0.5365 Loss_G: 3.0092 D(x): 0.7437 D(G(z)): 0.1574 / 0.0836
[1/5][50/1583] Loss_D: 0.4959 Loss_G: 5.4086 D(x): 0.9422 D(G(z)): 0.2960 / 0.0086
[1/5][100/1583] Loss_D: 0.2685 Loss_G: 3.6553 D(x): 0.8455 D(G(z)): 0.0640 / 0.0457
[1/5][150/1583] Loss_D: 0.6243 Loss_G: 4.6128 D(x): 0.8467 D(G(z)): 0.2878 / 0.0203
[1/5][200/1583] Loss_D: 0.4369 Loss_G: 2.8268 D(x): 0.7591 D(G(z)): 0.0871 / 0.0871
[1/5][250/1583] Loss_D: 0.4244 Loss_G: 3.7669 D(x): 0.8641 D(G(z)): 0.1952 / 0.0369
[1/5][300/1583] Loss_D: 0.7487 Loss_G: 2.5417 D(x): 0.6388 D(G(z)): 0.0948 / 0.1263
[1/5][350/1583] Loss_D: 0.5359 Loss_G: 2.9435 D(x): 0.6996 D(G(z)): 0.0836 / 0.0864
[1/5][400/1583] Loss_D: 0.3469 Loss_G: 2.7581 D(x): 0.8046 D(G(z)): 0.0755 / 0.1036
[1/5][450/1583] Loss_D: 0.5065 Loss_G: 2.8547 D(x): 0.7491 D(G(z)): 0.1494 / 0.0879
[1/5][500/1583] Loss_D: 0.3959 Loss_G: 3.3236 D(x): 0.8292 D(G(z)): 0.1328 / 0.0554
[1/5][550/1583] Loss_D: 0.6679 Loss_G: 5.8782 D(x): 0.9178 D(G(z)): 0.3802 / 0.0075
[1/5][600/1583] Loss_D: 0.8844 Loss_G: 1.9449 D(x): 0.5367 D(G(z)): 0.0326 / 0.1984
[1/5][650/1583] Loss_D: 0.8474 Loss_G: 2.0978 D(x): 0.6395 D(G(z)): 0.1883 / 0.1803
[1/5][700/1583] Loss_D: 0.4682 Loss_G: 5.1056 D(x): 0.8963 D(G(z)): 0.2520 / 0.0137
[1/5][750/1583] Loss_D: 0.4315 Loss_G: 4.0099 D(x): 0.8957 D(G(z)): 0.2441 / 0.0304
[1/5][800/1583] Loss_D: 0.4492 Loss_G: 4.1587 D(x): 0.9090 D(G(z)): 0.2656 / 0.0231
[1/5][850/1583] Loss_D: 0.7694 Loss_G: 1.2065 D(x): 0.5726 D(G(z)): 0.0254 / 0.3785
[1/5][900/1583] Loss_D: 0.3543 Loss_G: 4.0476 D(x): 0.8919 D(G(z)): 0.1873 / 0.0284
[1/5][950/1583] Loss_D: 0.5111 Loss_G: 2.3574 D(x): 0.7082 D(G(z)): 0.0835 / 0.1288
[1/5][1000/1583] Loss_D: 0.5802 Loss_G: 5.4608 D(x): 0.9395 D(G(z)): 0.3649 / 0.0077
[1/5][1050/1583] Loss_D: 1.0051 Loss_G: 2.4068 D(x): 0.5352 D(G(z)): 0.0322 / 0.1486
[1/5][1100/1583] Loss_D: 0.3509 Loss_G: 3.6524 D(x): 0.9101 D(G(z)): 0.2070 / 0.0387
[1/5][1150/1583] Loss_D: 0.9412 Loss_G: 5.4059 D(x): 0.9597 D(G(z)): 0.5325 / 0.0080
[1/5][1200/1583] Loss_D: 0.5332 Loss_G: 3.1298 D(x): 0.7943 D(G(z)): 0.2138 / 0.0630
[1/5][1250/1583] Loss_D: 0.6025 Loss_G: 3.5758 D(x): 0.8679 D(G(z)): 0.3182 / 0.0428
[1/5][1300/1583] Loss_D: 0.7154 Loss_G: 2.1555 D(x): 0.5657 D(G(z)): 0.0379 / 0.1685
[1/5][1350/1583] Loss_D: 0.4168 Loss_G: 2.1878 D(x): 0.7452 D(G(z)): 0.0645 / 0.1534
[1/5][1400/1583] Loss_D: 0.8991 Loss_G: 5.3523 D(x): 0.9256 D(G(z)): 0.4967 / 0.0074
[1/5][1450/1583] Loss_D: 0.4778 Loss_G: 3.8499 D(x): 0.8844 D(G(z)): 0.2655 / 0.0350
[1/5][1500/1583] Loss_D: 0.5049 Loss_G: 2.5450 D(x): 0.7880 D(G(z)): 0.1906 / 0.1010
[1/5][1550/1583] Loss_D: 1.0468 Loss_G: 1.9007 D(x): 0.4378 D(G(z)): 0.0346 / 0.2260
[2/5][0/1583] Loss_D: 0.5008 Loss_G: 3.5294 D(x): 0.9006 D(G(z)): 0.2844 / 0.0466
[2/5][50/1583] Loss_D: 0.5024 Loss_G: 2.3252 D(x): 0.7413 D(G(z)): 0.1450 / 0.1267
[2/5][100/1583] Loss_D: 0.7520 Loss_G: 2.0230 D(x): 0.5753 D(G(z)): 0.0835 / 0.1797
[2/5][150/1583] Loss_D: 0.3734 Loss_G: 2.7221 D(x): 0.8502 D(G(z)): 0.1689 / 0.0889
[2/5][200/1583] Loss_D: 0.5891 Loss_G: 2.6314 D(x): 0.7453 D(G(z)): 0.2076 / 0.1032
[2/5][250/1583] Loss_D: 1.1471 Loss_G: 3.5814 D(x): 0.8959 D(G(z)): 0.5563 / 0.0545
[2/5][300/1583] Loss_D: 0.5756 Loss_G: 3.1905 D(x): 0.8738 D(G(z)): 0.3128 / 0.0605
[2/5][350/1583] Loss_D: 0.5971 Loss_G: 2.9928 D(x): 0.8177 D(G(z)): 0.2657 / 0.0739
[2/5][400/1583] Loss_D: 0.6856 Loss_G: 3.8514 D(x): 0.8880 D(G(z)): 0.3835 / 0.0298
[2/5][450/1583] Loss_D: 0.6088 Loss_G: 1.7919 D(x): 0.6660 D(G(z)): 0.1227 / 0.2189
[2/5][500/1583] Loss_D: 0.7147 Loss_G: 2.6453 D(x): 0.8321 D(G(z)): 0.3531 / 0.1007
[2/5][550/1583] Loss_D: 0.5759 Loss_G: 2.9074 D(x): 0.8269 D(G(z)): 0.2833 / 0.0738
[2/5][600/1583] Loss_D: 0.5678 Loss_G: 2.6149 D(x): 0.7928 D(G(z)): 0.2516 / 0.0956
[2/5][650/1583] Loss_D: 0.9501 Loss_G: 1.1814 D(x): 0.5916 D(G(z)): 0.2322 / 0.3815
[2/5][700/1583] Loss_D: 0.4551 Loss_G: 2.5074 D(x): 0.8331 D(G(z)): 0.2047 / 0.1129
[2/5][750/1583] Loss_D: 0.4560 Loss_G: 2.3947 D(x): 0.7525 D(G(z)): 0.1240 / 0.1147
[2/5][800/1583] Loss_D: 1.1853 Loss_G: 5.1657 D(x): 0.9202 D(G(z)): 0.6049 / 0.0091
[2/5][850/1583] Loss_D: 0.5514 Loss_G: 3.0085 D(x): 0.8497 D(G(z)): 0.2890 / 0.0685
[2/5][900/1583] Loss_D: 0.6882 Loss_G: 1.8971 D(x): 0.6970 D(G(z)): 0.2332 / 0.1909
[2/5][950/1583] Loss_D: 1.1220 Loss_G: 0.7904 D(x): 0.4095 D(G(z)): 0.0570 / 0.4975
[2/5][1000/1583] Loss_D: 1.3335 Loss_G: 0.3115 D(x): 0.3347 D(G(z)): 0.0262 / 0.7661
[2/5][1050/1583] Loss_D: 1.7281 Loss_G: 0.8212 D(x): 0.2437 D(G(z)): 0.0261 / 0.5179
[2/5][1100/1583] Loss_D: 0.9401 Loss_G: 3.7894 D(x): 0.9033 D(G(z)): 0.5104 / 0.0349
[2/5][1150/1583] Loss_D: 0.8078 Loss_G: 3.9862 D(x): 0.9178 D(G(z)): 0.4608 / 0.0286
[2/5][1200/1583] Loss_D: 0.5182 Loss_G: 3.1859 D(x): 0.8568 D(G(z)): 0.2787 / 0.0554
[2/5][1250/1583] Loss_D: 0.5092 Loss_G: 2.3530 D(x): 0.8015 D(G(z)): 0.2122 / 0.1188
[2/5][1300/1583] Loss_D: 1.2668 Loss_G: 0.5543 D(x): 0.3424 D(G(z)): 0.0165 / 0.6271
[2/5][1350/1583] Loss_D: 0.7197 Loss_G: 3.8595 D(x): 0.9043 D(G(z)): 0.4208 / 0.0299
[2/5][1400/1583] Loss_D: 0.5428 Loss_G: 2.6526 D(x): 0.8873 D(G(z)): 0.3056 / 0.0961
[2/5][1450/1583] Loss_D: 0.6610 Loss_G: 4.2385 D(x): 0.9272 D(G(z)): 0.3985 / 0.0211
[2/5][1500/1583] Loss_D: 0.8172 Loss_G: 3.2164 D(x): 0.8811 D(G(z)): 0.4422 / 0.0612
[2/5][1550/1583] Loss_D: 0.6449 Loss_G: 3.8452 D(x): 0.9130 D(G(z)): 0.3813 / 0.0325
[3/5][0/1583] Loss_D: 0.7677 Loss_G: 1.7745 D(x): 0.5928 D(G(z)): 0.1388 / 0.2182
[3/5][50/1583] Loss_D: 0.7981 Loss_G: 2.9624 D(x): 0.8315 D(G(z)): 0.4131 / 0.0735
[3/5][100/1583] Loss_D: 0.5679 Loss_G: 1.8958 D(x): 0.7173 D(G(z)): 0.1667 / 0.1914
[3/5][150/1583] Loss_D: 0.8576 Loss_G: 1.5904 D(x): 0.5391 D(G(z)): 0.1158 / 0.2699
[3/5][200/1583] Loss_D: 0.8644 Loss_G: 1.6487 D(x): 0.5868 D(G(z)): 0.1933 / 0.2319
[3/5][250/1583] Loss_D: 0.5331 Loss_G: 3.0401 D(x): 0.8831 D(G(z)): 0.3022 / 0.0608
[3/5][300/1583] Loss_D: 1.2449 Loss_G: 2.9489 D(x): 0.8759 D(G(z)): 0.5865 / 0.0828
[3/5][350/1583] Loss_D: 1.7188 Loss_G: 0.5466 D(x): 0.2664 D(G(z)): 0.0539 / 0.6320
[3/5][400/1583] Loss_D: 0.5794 Loss_G: 2.7556 D(x): 0.7984 D(G(z)): 0.2640 / 0.0787
[3/5][450/1583] Loss_D: 0.6916 Loss_G: 3.1434 D(x): 0.8813 D(G(z)): 0.3955 / 0.0578
[3/5][500/1583] Loss_D: 0.8415 Loss_G: 1.9770 D(x): 0.6981 D(G(z)): 0.3120 / 0.1639
[3/5][550/1583] Loss_D: 0.6394 Loss_G: 2.4790 D(x): 0.8093 D(G(z)): 0.2990 / 0.1082
[3/5][600/1583] Loss_D: 0.7545 Loss_G: 1.6259 D(x): 0.6042 D(G(z)): 0.1454 / 0.2401
[3/5][650/1583] Loss_D: 0.5494 Loss_G: 2.1957 D(x): 0.8292 D(G(z)): 0.2727 / 0.1414
[3/5][700/1583] Loss_D: 1.5095 Loss_G: 5.1368 D(x): 0.9269 D(G(z)): 0.6897 / 0.0095
[3/5][750/1583] Loss_D: 0.4714 Loss_G: 2.1401 D(x): 0.8137 D(G(z)): 0.2101 / 0.1501
[3/5][800/1583] Loss_D: 0.7118 Loss_G: 3.2356 D(x): 0.8190 D(G(z)): 0.3579 / 0.0540
[3/5][850/1583] Loss_D: 0.6392 Loss_G: 1.6740 D(x): 0.6650 D(G(z)): 0.1402 / 0.2391
[3/5][900/1583] Loss_D: 0.5303 Loss_G: 2.8854 D(x): 0.7900 D(G(z)): 0.2204 / 0.0740
[3/5][950/1583] Loss_D: 0.6333 Loss_G: 2.1030 D(x): 0.6946 D(G(z)): 0.1882 / 0.1572
[3/5][1000/1583] Loss_D: 0.8715 Loss_G: 1.6630 D(x): 0.5222 D(G(z)): 0.0890 / 0.2590
[3/5][1050/1583] Loss_D: 0.6139 Loss_G: 3.1772 D(x): 0.8609 D(G(z)): 0.3400 / 0.0558
[3/5][1100/1583] Loss_D: 0.6673 Loss_G: 3.4143 D(x): 0.9044 D(G(z)): 0.3910 / 0.0435
[3/5][1150/1583] Loss_D: 0.6554 Loss_G: 3.4282 D(x): 0.8429 D(G(z)): 0.3347 / 0.0484
[3/5][1200/1583] Loss_D: 0.6184 Loss_G: 1.7371 D(x): 0.6531 D(G(z)): 0.1177 / 0.2132
[3/5][1250/1583] Loss_D: 0.8293 Loss_G: 3.1246 D(x): 0.7821 D(G(z)): 0.3883 / 0.0594
[3/5][1300/1583] Loss_D: 0.5211 Loss_G: 2.0112 D(x): 0.7308 D(G(z)): 0.1503 / 0.1637
[3/5][1350/1583] Loss_D: 0.7389 Loss_G: 1.4238 D(x): 0.5854 D(G(z)): 0.1181 / 0.2935
[3/5][1400/1583] Loss_D: 0.6608 Loss_G: 3.1928 D(x): 0.7803 D(G(z)): 0.2922 / 0.0580
[3/5][1450/1583] Loss_D: 0.6381 Loss_G: 3.4123 D(x): 0.8340 D(G(z)): 0.3337 / 0.0450
[3/5][1500/1583] Loss_D: 0.7027 Loss_G: 3.1943 D(x): 0.9058 D(G(z)): 0.4113 / 0.0556
[3/5][1550/1583] Loss_D: 0.6849 Loss_G: 2.9714 D(x): 0.8258 D(G(z)): 0.3499 / 0.0704
[4/5][0/1583] Loss_D: 0.7685 Loss_G: 1.7204 D(x): 0.5788 D(G(z)): 0.1084 / 0.2252
[4/5][50/1583] Loss_D: 0.6194 Loss_G: 1.4702 D(x): 0.6214 D(G(z)): 0.0700 / 0.2812
[4/5][100/1583] Loss_D: 0.5243 Loss_G: 2.4332 D(x): 0.8206 D(G(z)): 0.2515 / 0.1099
[4/5][150/1583] Loss_D: 0.8506 Loss_G: 1.0129 D(x): 0.5094 D(G(z)): 0.0647 / 0.4126
[4/5][200/1583] Loss_D: 1.1715 Loss_G: 2.5120 D(x): 0.5642 D(G(z)): 0.3481 / 0.1214
[4/5][250/1583] Loss_D: 0.4317 Loss_G: 2.7731 D(x): 0.8405 D(G(z)): 0.2088 / 0.0791
[4/5][300/1583] Loss_D: 1.2310 Loss_G: 0.4177 D(x): 0.3812 D(G(z)): 0.0576 / 0.6799
[4/5][350/1583] Loss_D: 0.5565 Loss_G: 2.7405 D(x): 0.8525 D(G(z)): 0.3005 / 0.0810
[4/5][400/1583] Loss_D: 0.4918 Loss_G: 3.5705 D(x): 0.8863 D(G(z)): 0.2833 / 0.0371
[4/5][450/1583] Loss_D: 0.6403 Loss_G: 2.7691 D(x): 0.8543 D(G(z)): 0.3406 / 0.0812
[4/5][500/1583] Loss_D: 0.5944 Loss_G: 1.4696 D(x): 0.6849 D(G(z)): 0.1325 / 0.2682
[4/5][550/1583] Loss_D: 0.8678 Loss_G: 4.1990 D(x): 0.9529 D(G(z)): 0.5105 / 0.0202
[4/5][600/1583] Loss_D: 0.8326 Loss_G: 1.1841 D(x): 0.5175 D(G(z)): 0.0679 / 0.3628
[4/5][650/1583] Loss_D: 0.5198 Loss_G: 2.4393 D(x): 0.7668 D(G(z)): 0.1943 / 0.1148
[4/5][700/1583] Loss_D: 0.8029 Loss_G: 4.0836 D(x): 0.8791 D(G(z)): 0.4448 / 0.0229
[4/5][750/1583] Loss_D: 0.8636 Loss_G: 2.0386 D(x): 0.5234 D(G(z)): 0.0899 / 0.1846
[4/5][800/1583] Loss_D: 0.5041 Loss_G: 3.0354 D(x): 0.8302 D(G(z)): 0.2301 / 0.0609
[4/5][850/1583] Loss_D: 0.7514 Loss_G: 1.2513 D(x): 0.5578 D(G(z)): 0.0899 / 0.3480
[4/5][900/1583] Loss_D: 0.6650 Loss_G: 1.2806 D(x): 0.6675 D(G(z)): 0.1925 / 0.3201
[4/5][950/1583] Loss_D: 0.5754 Loss_G: 3.0898 D(x): 0.8730 D(G(z)): 0.3233 / 0.0597
[4/5][1000/1583] Loss_D: 0.9327 Loss_G: 0.7588 D(x): 0.4674 D(G(z)): 0.0434 / 0.5174
[4/5][1050/1583] Loss_D: 0.9255 Loss_G: 0.9513 D(x): 0.5029 D(G(z)): 0.1161 / 0.4196
[4/5][1100/1583] Loss_D: 0.6573 Loss_G: 3.4663 D(x): 0.8755 D(G(z)): 0.3674 / 0.0403
[4/5][1150/1583] Loss_D: 0.9803 Loss_G: 1.2451 D(x): 0.4602 D(G(z)): 0.0978 / 0.3432
[4/5][1200/1583] Loss_D: 0.5560 Loss_G: 2.5421 D(x): 0.7617 D(G(z)): 0.2097 / 0.1020
[4/5][1250/1583] Loss_D: 0.7573 Loss_G: 1.9034 D(x): 0.6477 D(G(z)): 0.2158 / 0.1890
[4/5][1300/1583] Loss_D: 0.4733 Loss_G: 2.7071 D(x): 0.8271 D(G(z)): 0.2169 / 0.0882
[4/5][1350/1583] Loss_D: 1.0812 Loss_G: 1.1500 D(x): 0.5225 D(G(z)): 0.2278 / 0.3626
[4/5][1400/1583] Loss_D: 1.5454 Loss_G: 5.2881 D(x): 0.9620 D(G(z)): 0.7085 / 0.0089
[4/5][1450/1583] Loss_D: 0.3576 Loss_G: 3.1023 D(x): 0.8687 D(G(z)): 0.1726 / 0.0584
[4/5][1500/1583] Loss_D: 0.5330 Loss_G: 1.9979 D(x): 0.7277 D(G(z)): 0.1597 / 0.1680
[4/5][1550/1583] Loss_D: 0.8927 Loss_G: 4.1379 D(x): 0.9345 D(G(z)): 0.5081 / 0.0224
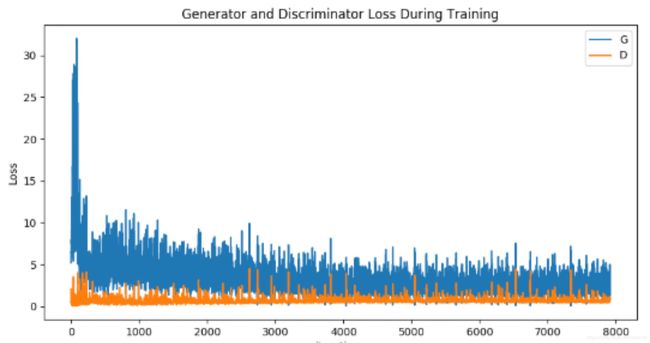
5.6 结果
从三个不同方面看实验结果:
- 看G和D两个损失函数的变化
- 看每轮epoch训练G生成图片的结果
- 对比一批生成图片和一批真实图片(64张)
a.loss变化
plt.figure(figsize=(10,5))
plt.title("Generator and Discriminator Loss During Training")
plt.plot(G_losses,label="G")
plt.plot(D_losses,label="D")
plt.xlabel("iterations")
plt.ylabel("Loss")
plt.legend()
plt.show()
#%%capture
fig = plt.figure(figsize=(8,8))
plt.axis("off")
ims = [[plt.imshow(np.transpose(i,(1,2,0)), animated=True)] for i in img_list]
ani = animation.ArtistAnimation(fig, ims, interval=1000, repeat_delay=1000, blit=True)
HTML(ani.to_jshtml())
c.对比真假图片
# Grab a batch of real images from the dataloader
real_batch = next(iter(dataloader))
# Plot the real images
plt.figure(figsize=(15,15))
plt.subplot(1,2,1)
plt.axis("off")
plt.title("Real Images")
plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(device)[:64], padding=5, normalize=True).cpu(),(1,2,0)))
# Plot the fake images from the last epoch
plt.subplot(1,2,2)
plt.axis("off")
plt.title("Fake Images")
plt.imshow(np.transpose(img_list[-1],(1,2,0)))
plt.show()
6.下一步
- Train for longer to see how good the results get
多训练几次,如增加epoch看效果
- Modify this model to take a different dataset and possibly change the size of the images and the model architecture
换其他数据集、或者调整一些模型结构
- Check out some other cool GAN projects here
试试其他有趣的GAN应用–https://github.com/nashory/gans-awesome-applications
- Create GANs that generate music
用GAN生成音乐
7.参考:
https://pytorch.org/tutorials/beginner/dcgan_faces_tutorial.html#
https://github.com/soumith/ganhacks#authors