【博弈论】博弈论基础知识

本学期选了博弈论的通识课，现将其基础知识点总结一下：

1.博弈论（Game Theory):博弈论也称游戏论、对策论，是研究相互依赖、相互影响的决策主体的理性决策行为以及这些决策的均衡结果的理论。

2.博弈论的基本构成要素：
1.参与者，参与博弈的利益主体叫做参与者（玩家，局中人）。在二人博弈中，有两个参与者；在三人博弈中，有三个参与者；在多人博弈中，有多个参与者；
2.策略，在给定条件博弈中，参与者完整的一套行动计划叫做策略；
3.收益，支付( Pay-off )：博弈结束时，各方得到的收益，参与博弈的多个参与者的收益可以用一个矩阵或框图表示，这样的矩阵或框图就叫做收益矩阵，如下图；
4.信息，是指参与人在作出决策前，所了解的关于得失函数或支付函数的所有知识，包括其他参与人的策略选择给自己带来的收益或损失，以及自己的策略选择给自己带来的收益或损失；
5.均衡，当博弈的所有参与者都不想改换策略时所达到的稳定状态叫做均衡，均衡的结果叫做博弈的解。

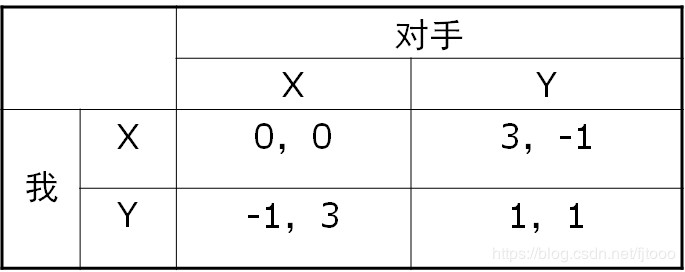
3.零和博弈：即“快乐必须建立在别人的痛苦之上”，意思是博弈中甲方的收益，必然是乙方的损失，即各博弈方得益之和为零。非零和博弈：博弈中各方的收益或损失的总和不是零值。零和博弈是利益对抗程度最高的博弈。

4.严格优势策略（Strictly dominated strategy）：也叫“占优策略”：无论对方作何选择，这一策略是严格优于其他策略。如上图中，无论对手选择X还是Y，我方选择X的收益都要比Y高（0>-1,3>1），那么X就是我的严格优势策略，同理，X是对手的严格优势策略，则这个博弈的解为（X,X）。

5.囚徒困境：两个罪犯被审问时有招供和不招供两种选择，如果对方不招供而自己招供，自己就会得到宽大处理，其收益矩阵如下：

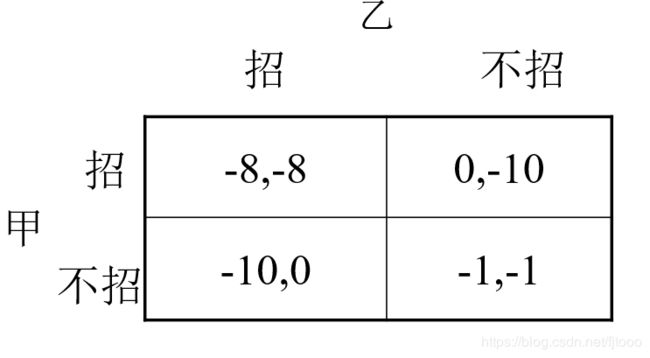
可见，对于甲乙两个囚徒来说，“招”都是各自的严格优势策略，博弈的解是（招，招），所以虽然看起来两者都不招可以两全其美，但是两个理性的囚徒都会选择招，导致两败俱伤。

6.占优策略均衡：在博弈中，由局中人的上策构成的均衡称为占优策略（上策）均衡。上图囚徒困境的解（招，招）就是占优策略均衡。

7.单方占优策略均衡：在一方没有占优策略而另一方有的时候，预期另一方按占优策略行动而选择自己的占优策略。如下图：

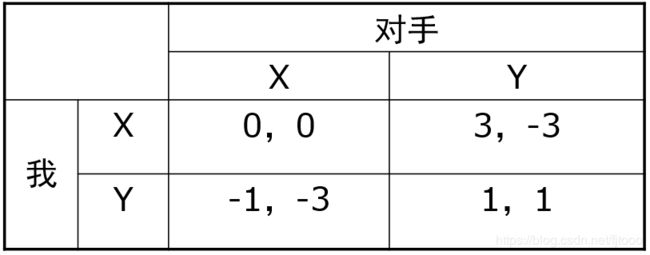
发现我方有严格优势策略：X，而对方没有，那么对方会依据我方选X而选择X（0>-3)，故该博弈的解为（X,X）。

8.智猪博弈：猪圈中有一头大猪和一头小猪，在猪圈的一端有一个踏板，每踩一下，位于猪圈另一端的食槽中就会有10单位的猪食进槽，但每踩一下踏板会耗去相当于2单位猪食的成本。如果大猪踩踏板，则大猪吃到6单位食物，小猪能吃到4单位食物，除去大猪消耗掉的2单位食物，两猪收益4:4，如果两猪一起踩踏板，则大猪吃7单位，小猪吃3单位食物，除去消耗，两猪收益 5:1，如果小猪先踩踏板，大猪吃9单位而小猪吃1单位食物，除去小猪的消耗，两猪收益9:-1，如果都不动，两头猪的收益自然都是0 。每只猪都可以选择“踩”或者“不踩”踏板。其收益矩阵如下：
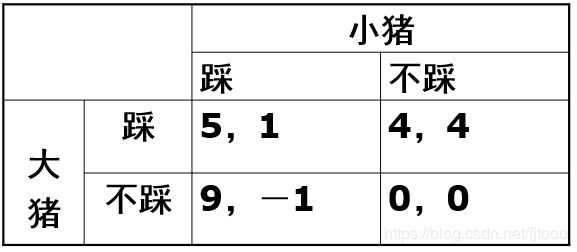经过分析，小猪有严格优势策略“不踩”（1<4，-1<0），而没有严格优势策略的大猪在已知这点后，会选择“踩”（4>0），则该博弈的解为（踩，不踩）。“智猪博弈”告诉我们，谁先去踩踏板，就会造福其他人，但多劳不一定多得。破解智猪博弈的方法之一是：减短食槽到猪的距离，也就是减少取踩踏板的成本，这样小猪不至于由于成本太高而收入太少选择不去踩踏板，大猪小猪都会争相踩踏板，这是一个最好的方案，成本不高，但收获最大。

9.纳什均衡（Nash Equilibrium）：在给定其他参与者策略情况下，没有一个参与者能通过单方面改变自己的策略而使自己的得益提高，从而没有人有积极性打破这种均衡。纳什均衡是满足给定对手的行为，各博弈方所做的是它能做的最好的行为。

10.相对优势策略划线法：划线法是一个求解纳什均衡的方法。纳什均衡是指我所做的是给定你所做的我所能做的最好的，那么求解纳什均衡，就是找出各个相对优势策略，如图：

对于男生来说，女生如果选看足球，自己就选看足球（5>-2）并在相应支付数字下面划线，如果女生选逛街，自己就选逛街（2>-1)，并划线，对女生同理。如果哪个格子里两个数字都被划线，那么这个各自对应的双方相对优势策略的组合，就是一个纳什均衡。所以该博弈的解是（看足球，看足球）和（逛街，逛街）。

11.最大最小策略：是指博弈者所采取的策略是自己能够获得的最小收入最大化。
要达到优势策略均衡或纳什均衡是需要绝对理性的。任何出现了一点错误将可能使博弈者蒙受巨大的损失，因而可能有player会采取比较保守的策略，那就是最大最小策略，即使自己的最小收入最大的策略，如图：

对于该收益矩阵，纳什均衡应是（有新品，无新品）和（无新品，有新品）；如果双方都采取最大最小策略，均衡结果是（无新品，无新品）。

12.古诺模型：古诺模型又称古诺双寡头模型，属于纳什均衡的一个应用。以两厂商产量竞争为例。设q1和q2是厂商1和厂商2的产量，Q是总产量，c1和c2是两个厂商生产产品的单位成本，u1和u2是两厂商的利润，P（Q）是市场需求函数，P是单价。设：

计算利润有：

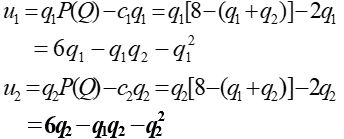
两者都想让自己的利润最大，那么将u1对p1求导，u2对p2求导，求利润的最大值：

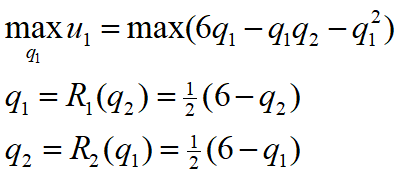
这里的R1 (q2)是企业1的反应函数，它表明企业1对企业2的所有可能产量所作出的最优产量决策，R2（q1）是企业2的反映函数，它表明企业2对企业1的所有可能产量所作出的最优产量决策。

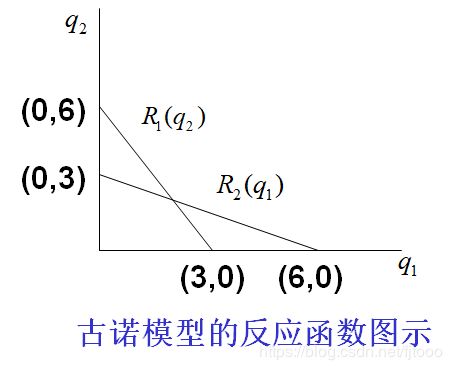也就是说，如果企业1已知企业二的产量为q2，那么将q2带入R1，得到q1就是企业1的最优产量，企业二同理。那么以动态的视角看整个博弈过程，如下图：

整个博弈过程最后的解应该为两个反应函数的交点NE所对应的q1和q2，如何解释呢？我们从A点开始梳理，如果现在厂商1决定不生产产品，即q1=0，那么R2对应的A点所对应的q2即为厂商2目前的最优产量决策；此时厂商1看到厂商2已经最优了（因为均衡点在R2上），那么就会调整自己的产量，现在q2固定，要使q1最大，那么必定是找q2在R1上的点，即B点，同理，接下来厂商2会调整到C点……，最终在NE点达到均衡。其实这个结论很明显，厂商1和厂商2都想让自己的收益最大，那么最后的均衡点一定既在R1上又在R2上，满足条件的只有交点NE。

13.纯策略和混合策略：：纯策略是指参与者在他的策略空间中选取唯一确定的策略。纯策略是参与者一次性选取的，并且坚持他选取的策略；所谓混合策略采取的不是唯一的策略，而是其策略空间上的概率分布。混合策略是参与者在各种备选策略中采取随机方式选取的。

14.混合策略纳什均衡：当自己的策略选择显然有很强烈的倾向性时，可以采用混合策略，使用混合策略达到的纳什均衡称为混合策略纳什均衡。纯策略的纳什均衡只是博弈的一种特例。

15.支付等值法：支付等值法是一种求解混合策略纳什均衡的方法，其思想是求参与者各个选择的收益的期望，并令它们相等。如下图政府与流浪汉的博弈：政府想帮助流浪汉，但前提是后者必须试图寻找工作，否则，不予帮助；而流浪汉若知道政府采用救济策略的话，他就不会寻找工作。他们只有在得不到政府救济时才会寻找工作。他们获得的支付如图所示：

设政府和流浪汉都是用混合策略。

对于流浪汉选择纳什均衡的混合策略，政府不会偏离他的混合策略，因此政府在救济与不救济之间是无差异的，即：

对于政府选择纳什均衡的混合策略，流浪汉不会偏离他的混合策略，因此流浪汉在寻找工作与游闲之间是无差异的，即：

16.动态博弈：如果局中人在进行行动选择时有先后顺序之分，这种博弈叫“序贯博弈”，是“动态博弈”。后行动者可以观察到先行动者做了什么选择，
每个参与人都必须这样思考问题：如果我如此选择，对方将如何应对？如果我是他，我将会如何行动？给定他的应对，什么是我的最优选择？

17.博弈树：在动态博弈过程中，将每一步双方的选择和后果还有收益画成树的形式，称作博弈树。举例：甲在开采一价值4千万元的金矿时缺1千万元资金，而乙正好有1千万元资金可以投资。此时，假设甲想说服乙将这1千万元资金借给自己开矿，并允诺在采到金子后与乙对半分成，乙是否该将钱借给甲呢？该博弈的博弈树为（注意：括号左边写先做决定的参与者的收益，右边写后做决定的参与者的收益）：

18.逆向归纳法(backward induction) ：从动态博弈的最后一个阶段博弈方的行为开始分析，逐步倒推回前一个阶段相应博弈方的行为选择，一直到第一个阶段的分析方法，称为“逆向归纳法”。逆向归纳法是动态博弈分析最重要、基本的方法。比如，在上面的的开金矿博弈中，从最后开始逆向分析，甲会选择不分，因为2<4，而乙知道甲不分而情况下，会选择不借，因为1 >0。

19.子博弈完美纳什均衡：如果动态博弈中各博弈方的策略在动态博弈本身和所有子博弈中都构成一个纳什均衡，则称该策略组合为一个“子博弈完美纳什均衡（Sub-game Perfect Nash Equilibrium，SPNE）”。子博弈完美纳什均衡本身也是纳什均衡，只不过是比纳什均衡更强的一个均衡概念，子博弈完美纳什均衡在动态博弈分析中的地位与纳什均衡在静态博弈分析中一样，是最核心的分析概念，求完美信息动态博弈的子博弈完美纳什均衡最基本的方法是逆向归纳法。