算法和数据结构（Python）——回溯法求排列组合

适用情况

需要找数组中数字的组合或排列

模式概括

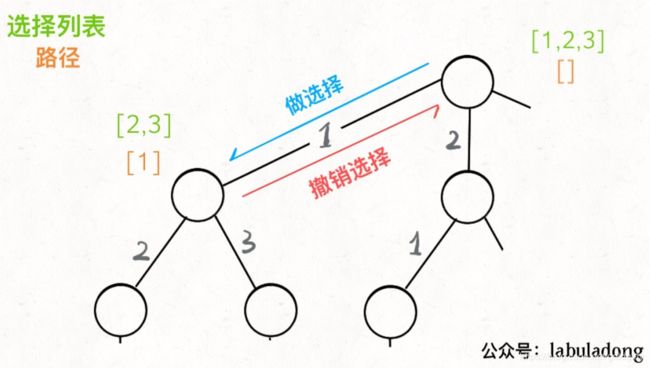
回溯法

res = []
tmp = []
if <1.设置条件：把需要的当前列表加入res>:
	res.append(当前列表)
	return res
for 选择 in 选择列表:
	<2.做选择> 
	<3.递归调用> backtrack(选择列表，当前列表，res)
	<4.撤销选择>

图解

例一 全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。
示例:
Input: [1,3,5]
Output: [1,3,5], [1,5,3], [3,1,5], [3,5,1], [5,1,3], [5,3,1]

解题思路：
结合回溯法的模式，需要特别考虑的是：

1. <满足条件>到达底层的条件就是选择列表nums为空

def permute(self, nums: List[int]) -> List[List[int]]:
        # 函数输入为空时的特殊情况
        if not nums: return nums
        # 参数赋值初始化
        res = []
        tmp = []
        # 调用backtrack函数，在类（class Solution）中要用self调用函数
        self.backtrack(nums, tmp, res)
        return res
    
    def backtrack(self, nums, tmp, res):   # nums是选择列表，tmp是当前选择
        #<满足条件> 到达底层的条件就是选择列表nums为空
        if not nums:
            # 错误写法 result.append(tem_result[]) 这样把地址传入，后面回退的时候会是一堆空列表
            res.append(tmp[:])

        for i in range(len(nums)):
            #<做出选择> 把选择列表中的元素append到当前选择中
            tmp.append(nums[i])
            # 
            # nums[0:i] + nums[i+1:]就是把选了的nums[i]去掉，更新选择列表nums
            self.backtrack(nums[0:i] + nums[i+1:], tmp, res) 
            # <撤销选择> 上面的调用结束即从下一层回溯到这一层，这时要更新当前选择tmp
            tmp.pop()

例二 子集

leetcode 78 （medium）给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

示例:
Input: [1, 5, 3]
Output: [], [1], [5], [3], [1,5], [1,3], [5,3], [1,5,3]

方法一：回溯法，递归

解题思路
结合回溯法模式，需要特别考虑的是：

1. <满足条件>因为所有出现的当前列表都是子集，不用设置条件，把所有tmp加到res中
2. 不能从选择列表中取所有元素，因为找子集只考虑当前元素之后的元素们，不能出现重复元素，所以要设起始点idx排除用过的元素，idx影响的是range的范围（选择列表）。递归调用时，因为 nums 不包含重复元素，并且每一个元素只能使用一次，所以下一次搜索从 i + 1 开始。

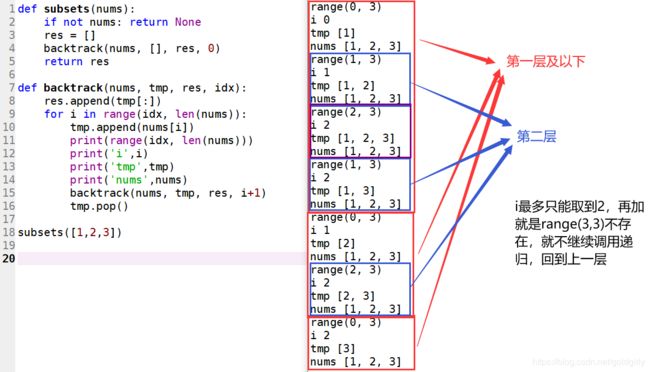
class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        if not nums: return None
        res = []
        self.backtrack(nums, [], res, 0)
        return res

    def backtrack(self, nums, tmp, res, idx):
        # <满足条件>所有出现的当前列表都是子集，不用条件，直接append到res
        res.append(tmp[:])
        # 只考虑当前元素之后的元素们，要设起始点排除用过的元素
        for i in range(idx, len(nums)):
            # <做选择>
            tmp.append(nums[i])
            # <递归调用>
            # 因为 nums 不包含重复元素，并且每一个元素只能使用一次，所以下一次搜索从 i + 1 开始
            self.backtrack(nums, tmp, res, i+1)
            # <撤销选择>
            tmp.pop()

方法二：迭代

解题思路：
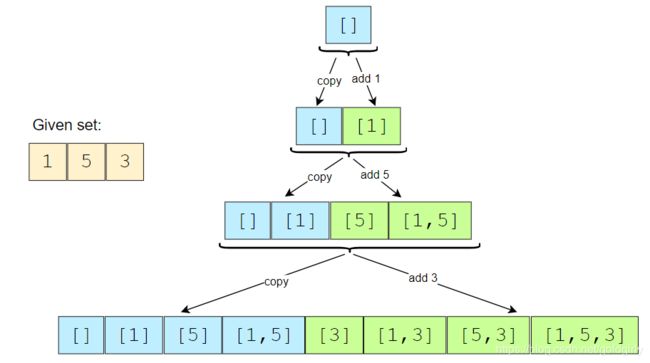
迭代，从空元素开始，循环每加入一个数组中的数值都相当于在上一个数组中的每项加入一个这个数值，再append到这个结果里

def subsets(nums):
    res = []
    res.append([])
    # 大循环，取出数组内的每个元素
    for i in nums:
        #for j in res: #不要直接循环列表，用索引循环
            # a = j.append(i) 这里j是列表，但不能这么写
        # 小循环，取出结果的每个索引
        for j in range(len(res)):
            a = list(res[j])
            # append大循环取出的元素
            a.append(i)   #不要写成b = a.append(a)
            res.append(a)
    return res

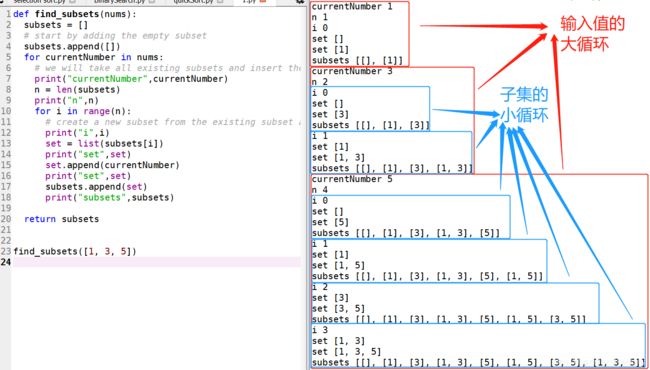
注意每次的小循环是循环subsets表中的元素（如上图第二层里的 [],[1]），取数组中的一个元素（如 5）append到[]里变成[5]，然后再append到subsets表。

例三 组合

leetcode 77 （medium）给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。
输入: n = 4, k = 2
输出: [[2,4], [3,4], [2,3], [1,2], [1,3], [1,4]]

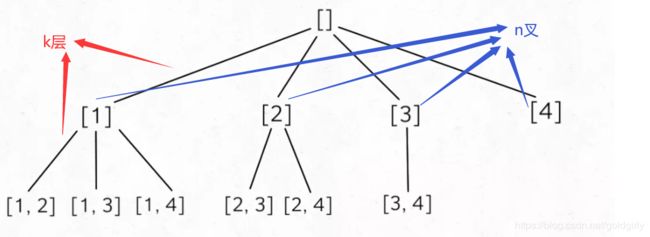
解题思路：

1. 画出n叉树分析
   
   k 限制了树的高度，n 限制了树的宽度，想到k作为<满足条件>，n用来创建<选择列表>
2. 跟子集一样，这里用过的元素不能再出现，要在range选择列表中设置起始点idx排除已经用过的元素

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        if not n or not k:
            return None

        nums = range(1, n+1) 
        res = []
        self.backtrack(nums, [], res, k, 0)
        return res

    def backtrack(self, nums, tmp, res, k, idx):
        # <满足条件> k限制树的高度，达到高度时加上当前列表tmp
        if len(tmp) == k:
            res.append(tmp[:])

        # 参考子集的做法，设置起始点idx用来排除已经用过的元素
        for i in range(idx, len(nums)):
            # <做选择>
            tmp.append(nums[i])
            # <递归调用>
            self.backtrack(nums, tmp, res, k, i+1)
            # <撤销选择>
            tmp.pop()

在框架基础上的一点优化，直接用n限制宽度

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        if not n or not k:
            return None
        res = []
        self.backtrack(n, [], res, k, 1)
        return res

    def backtrack(self, n, tmp, res, k, idx):
        if len(tmp) == k:
            res.append(tmp[:])
        # 优化代码：不用设nums，n就是nums的索引
        for i in range(idx, n+1):  
            tmp.append(i)
            self.backtrack(n, tmp, res, k, i+1)
            tmp.pop()

参考
labuladong的算法小抄