机器学习训练秘籍_学习笔记

本文主要参考“吴恩达deeplearning.ai——机器学习训练秘籍”（https://accepteddoge.github.io/machine-learning-yearning-cn/）进行学习整理的笔记。

一、训练集、开发集、测试集

训练集（training set）用于运行你的学习算法。

开发集（development set）用于调整参数，选择特征，以及对学习算法作出其它决定。有时也称为留出交叉验证集（hold-out cross validation set）。

测试集（test set）用于评估算法的性能，但不会据此决定使用什么学习算法或参数。

机器学习中的，一种常见的启发式策略是将 30% 的数据用作测试集，这适用于数据量规模一般的情况（比如 100 至 10,000 个样本）。但是在大数据时代，实际上开发集和测试集的比例会远低30%。

开发集和测试集应该服从同一分布

举个例子，假设你的团队开发了一套能在开发集上运行性能良好，却在测试集上效果不佳的系统。如果开发集和测试集分布相同，那么你就会非常清楚地知道问题在哪：在开发集上过拟合了（overfit）。解决方案显然就是获得更多的开发集数据。但是如果开发集和测试集来自不同的分布，解决方案就不那么明确了。

在处理第三方基准测试（benchmark）问题时，提供方可能已经指定了服从不同分布的开发集和测试集数据。与数据分布一致的情况相比，此时运气带来的性能影响将超过你所使用的技巧带来的影响。找到能够在某个分布上进行训练，并能够推广到另一个分布的学习算法，是一个重要的研究课题。但如果你想要在特定的机器学习应用上取得进展，而不是搞研究，我建议你尝试选择服从相同分布的开发集和测试集数据，这会让你的团队更有效率。

特例：

比如大型的神经网络，对于猫咪检测器的示例，我们不会将用户上传的所有 10000 个图像放到开发/测试集合中，而是将其中 5000 张放入。 这样的话，训练集中的 205000 个样本的分布将来自现有的开发/测试集，以及 200000 张网络图片。

添加额外的 20000 张图片会产生以下影响：

它给你的神经网络提供了更多关于猫咪外貌的样本。这是很有帮助的，因为互联网图片和用户上传的移动应用图片确实有一些相似之处。你的神经网络可以将从互联网图像中获得的一些知识应用到移动应用图像中。

它迫使神经网络花费部分容量来学习网络图像的特定属性（比如更高的分辨率，不同画面结构图像的分布等等）。如果这些属性与移动应用图像有很大的不同，那么它将“耗尽”神经网络的一些表征能力，导致从移动应用图像的分布识别数据的能力就会降低，而这正是你真正关心的东西。从理论上讲，这可能会损害算法的性能。

训练集：这是算法将学习的数据（例如，互联网图像+移动应用图像）。这并不需要我们从与真正关心的相同分布（开发/测试集分布）的数据中提取。

训练开发集：这些数据来自与训练集相同的分布（例如，互联网图像+移动应用图像）。它通常比训练集要小；它只需要足够大到来评估和跟踪我们的学习算法的进展。

开发集：这是从与测试集相同分布的数据中抽取出来的，它反映了我们最终关心的数据的分布（例如，移动应用图像） 。

测试集：这是从与开发集相同分布的数据中抽取出来的（例如，移动应用图像）。

有了这四个独立的数据集，你现在可以评估：

训练误差，对训练集进行评估。

该算法能够泛化到与训练集相同分布数据的能力，并对训练开发集进行评估。

算法在你实际关心的任务上的性能，通过对开发集 和/或 测试集评估。

开发集的规模应该大到足以区分出你所尝试的不同算法间的性能差异。例如，如果分类器 A 的准确率为 90.0% ，而分类器 B 的准确率为 90.1% ，那么仅有 100 个样本的开发集将无法检测出这 0.1% 的差异。相比我所遇到的机器学习问题，一个样本容量为 100 的开发集的规模是非常小的。通常来说，开发集的规模应该在 1,000 到 10,000 个样本数据之间，而当开发集样本容量为 10,000 时，你将很有可能检测到 0.1% 的性能提升。

从理论上说，还可以检测算法的变化是否会在开发集上造成统计学意义上的显著差异。 然而在实践中，大多数团队并不会为此而烦恼（除非他们正在发表学术研究论文），而且我在检测过程中并没有发现多少有效的统计显著性检验。

用于选择开发集大小的大多数指导原则也适用于训练开发集。

拥有开发集、测试集和单值评估指标可以帮你快速评估一个算法，从而加速迭代过程。

在不同的分布上训练集与开发/测试集的选择？

1. 如果有足够的计算能力来构建一个足够大的神经网络，可以考虑对训练集额外加入不同于开发集/测试集的数据。相反，应该更加关注训练数据，需要与开发/测试集的分布相匹配
2. 考虑对开发/测试集额外加入不同于训练集的数据。例如，假设你的开发/测试集主要包含一些内容是人员、地点、地标、动物的任意图片。同时假设集合里面有大量的历史文档扫描图片，这些文件不包含任何类似猫的东西，它们看起来和开发/测试集的分布完全不同，没有必要将这些数据作为负样本，你的神经网络几乎没有任何东西可以从这些数据中学习，加入它们将会浪费计算资源和神经网络的表征能力。但它们可以应用到开发/测试集中，

二、单值评估指标、优化指标、满意度指标

单值评估指标（single-number evaluation metric）有很多，分类准确率就是其中的一种。相比之下，查准率（Precision，又译作精度）和查全率（Recall，又译作召回率）均不是单值评估指标，可以使用二者的平均值，F1分数（F1 score），加权平均值等指标。

当开发集和评估指标不再能给团队一个正确的导向时，就尽快修改它们：(i) 如果你在开发集上过拟合，则获取更多的开发集数据。(ii) 如果开发集和测试集的数据分布和实际关注的数据分布不同，则获取新的开发集和测试集。 (iii) 如果评估指标不能够对最重要的任务目标进行度量，则需要修改评估指标。

三、误差分析

误差分析（Error Analysis） 指的是检查被算法误分类的开发集样本的过程，以便帮助你找到造成这些误差的原因。这将协助你确定各个项目的优先级并且获得探索新方向的灵感。

假设你已检查了100 个开发集的误分类样本，可以得到下面的表格：

图像                    狗     大猫       模糊       备注

1                         √                                   不常见的美国比特犬

2                                                √

3                                  √           √      狮子；雨天在动物园拍摄的图片

4                                  √                   树木后的美洲豹

…                     …         …         …

占全体比例      8%       43%      61%

查看误分类样本的这一过程称为误差分析。在上面的例子中，如果只有 5% 误分类的图像是狗，那么无论你在狗的问题上做多少的算法改进，最终都不会消除超过原有的 5% 误差 . 也即是说 5% 是该计划项目所能起到帮助的“上限”（最大可能值）。所以如果整个系统当前的精度为 90%（对应误差为 10%），那么这种改进最多能将精度提升到 90.5% （对应误差下降到 9.5% ， 改进了原有 10% 误差其中的 5%）。

相反，如果你发现 50% 的误分类图像是狗，那就可以自信地说这个项目将效果明显，它可以将精度从 90% 提升到 95% （相对误差减少 50%，整体误差由 10% 下降到 5%）。

“误标注”指的是图像在使用算法处理前，已经被负责标注的人员进行了错误的标注，也就是说，某个样本  的分类标签（label） 的值并不正确。例如，一些不是猫的图片被误标注为猫，反之亦然。如果你不确定这些被误标注的图片是否起着关键作用，可以添加一个类别来跟踪记录误标注样本的比例：

图像              狗          大猫       模糊       误标注  备注

…

89                                                                √            标注者忽略了背景中的猫

99                                 √

100                                                               √            猫的画像；非真猫

占全体比例        8%           43%       61%         6%

将开发集明确地分为 Eyeball 和 Blackbox 开发两个子集将很有帮助，它使你了解在人为的误差分析过程中 Eyeball 开发集何时开始发生过拟合。

Eyeball 和 Blackbox 开发集该设置多大？

假设你的分类器有 5% 的错误率。为了确保在 Eyeball 开发集中有约 100 个误分类的样本，样本开发集应该有约 2000 个样本（因为 0.05 * 2000 = 100）。分类器的错误率越低，为了获得足够多的错误样本进行误差分析，需要的 Eyeball 开发集就越大。

Blackbox 开发集有约 1000-10000 个样本是正常的 。完善一下该陈述，一个有 1000-10000 个样本的 Blackbox 开发集通常会为你提供足够的数据去调超参和选择模型，即使数据再多一些也无妨。而含有 100 个样本的 Blackbox 开发集虽然比较小，但仍然是有用的。

在 Eyeball 和 Blackbox 开发集之间，我认为 Eyeball 开发集更加重要（假设你正在研究一个人类能够很好解决的问题，检查这些样本能使得你更有洞悉力）。如果你只有一个 Eyeball 开发集，你可以在这个开发集上进行误差分析、模型选择和超参数调整，缺点是过拟合开发集的风险更大。

四、偏差和方差：误差的两大来源

粗略地说，偏差指的是算法在大型训练集上的错误率；方差指的是算法在测试集上的表现低于训练集的程度。当你使用均方误差（MSE）作为误差度量指标时，你可以写下偏差和方差对应的两个公式，并且证明总误差=偏差+方差。但在处理机器学习问题时，此处给出的偏差和方差的非正式定义已经足够。

最优错误率（“不可避免偏差”）：14%。假设我们决定，即使是世界上最好的语音系统，仍会有 14% 的误差。我们可以将其认为是学习算法的偏差“不可避免”的部分。最优错误率也被称为贝叶斯错误率（Bayes error rate），或贝叶斯率

可避免偏差：1%。即训练错误率和最优误差率之间的差值。

方差：15%。即开发错误和训练错误之间的差值。

如果可避免偏差值是负的，即算法在训练集上的表现比最优错误率要好。这意味着你正在过拟合训练集，并且算法已经过度记忆（over-memorized）训练集。你应该专注于有效降低方差的方法，而不是选择进一步减少偏差的方法。

偏差 = 最佳误差率（“不可避免偏差”）+ 可避免的偏差

加大模型的规模通常可以减少偏差，但也可能会增加方差和过拟合的风险。然而，这种过拟合风险通常只在你不使用正则化技术的时候出现。如果你的算法含有一个精心设计的正则化方法，通常可以安全地加大模型的规模，而不用担心增加过拟合风险。

如果具有较高的可避免偏差，那么加大模型的规模（例如通过添加层/神经元数量来增加神经网络的大小）。

如果具有较高的方差，那么增加训练集的数据量。

假设你正在应用深度学习方法，使用了 L2 正则化和 dropout 技术，并且设置了在开发集上表现最好的正则化参数。此时你加大模型规模，算法的表现往往会保持不变或提升；它不太可能明显地变差。这种情况下，不使用更大模型的唯一原因就是这将使得计算代价变大。

减少可避免偏差的技术

加大模型规模（例如神经元/层的数量）：这项技术能够使算法更好地拟合训练集，从而减少偏差。当你发现这样做会增大方差时，通过加入正则化可以抵消方差的增加。

根据误差分析结果修改输入特征：假设误差分析结果鼓励你增加额外的特征，从而帮助算法消除某个特定类别的误差。（我们会在接下来的章节深入讨论这个话题。）这些新的特征对处理偏差和方差都有所帮助。理论上，添加更多的特征将增大方差；当这种情况发生时，你可以加入正则化来抵消方差的增加。

减少或者去除正则化（L2 正则化，L1 正则化，dropout）：这将减少可避免偏差，但会增大方差。

修改模型架构（比如神经网络架构）使之更适用于你的问题：这将同时影响偏差和方差。

有一种方法并不能奏效：

添加更多的训练数据：这项技术可以帮助解决方差问题，但它对于偏差通常没有明显的影响。

减少方差的技术

添加更多的训练数据：这是最简单最可靠的一种处理方差的策略，只要你有大量的数据和对应的计算能力来处理他们。

加入正则化（L2 正则化，L1 正则化，dropout）：这项技术可以降低方差，但却增大了偏差。

加入提前终止（例如根据开发集误差提前终止梯度下降）：这项技术可以降低方差但却增大了偏差。提前终止（Early stopping）有点像正则化理论，一些学者认为它是正则化技术之一。

通过特征选择减少输入特征的数量和种类：这种技术或许有助于解决方差问题，但也可能增加偏差。稍微减少特征的数量（比如从 1000 个特征减少到 900 个）也许不会对偏差产生很大的影响，但显著地减少它们（比如从 1000 个特征减少到 100 个，10 倍地降低）则很有可能产生很大的影响，你也许排除了太多有用的特征。在现代深度学习研究过程中，当数据充足时，特征选择的比重需要做些调整，现在我们更可能将拥有的所有特征提供给算法，并让算法根据数据来确定哪些特征可以使用。而当你的训练集很小的时候，特征选择是非常有用的。

减小模型规模（比如神经元/层的数量）：谨慎使用。这种技术可以减少方差，同时可能增加偏差。然而我不推荐这种处理方差的方法，添加正则化通常能更好的提升分类性能。 减少模型规模的好处是降低了计算成本，从而加快了你训练模型的速度。如果加速模型训练是有用的，那么无论如何都要考虑减少模型的规模。但如果你的目标是减少方差，且不关心计算成本，那么考虑添加正则化会更好。

下面是两种额外的策略，和解决偏差问题章节所提到的方法重复：

根据误差分析结果修改输入特征：假设误差分析的结果鼓励你创建额外的特征，从而帮助算法消除某个特定类别的误差。这些新的特征对处理偏差和方差都有所帮助。理论上，添加更多的特征将增大方差；当这种情况发生时，加入正则化，这可以消除方差的增加。

修改模型架构（比如神经网络架构）使之更适用于你的问题：这项策略将同时影响偏差和方差。

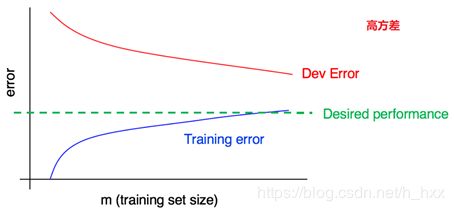
五、绘制学习曲线

存在训练集噪声致使难以正确理解曲线的变化时，有两种解决方案：

与其只使用 10 个样本训练单个模型，不如从你原来的 100 个样本中进行随机有放回抽样，选择几批（比如 3-10 ）不同的 10 个样本进行组合。在这些数据上训练不同的模型，并计算每个模型的训练和开发错误。最终，计算和绘制平均训练集误差和平均开发集误差。

如果你的训练集偏向于一个类，或者它有许多类，那么选择一个“平衡”子集，而不是从 100 个样本中随机抽取 10 个训练样本。例如，你可以确保这些样本中的 2/10是正样本，8/10 是负样本。更常见的做法是，确保每个类的样本比例尽可能地接近原始训练集的总体比例。

在实践中，用有放回抽样和无放回抽样的差异不大，但是前者更为常见。

六、构建机器学习系统

处理人类擅长的任务时：

1、易于从人为标签中获取数据。

2、基于人类直觉进行误差分析。

3、使用人类表现水平来估计最优错误率，并设置可达到的“期望错误率”。

处理人类不擅长的任务时：

1、获取标签数据很难。​

2、人类的直觉难以依靠。

3、最优错误率和合理的期望错误率难以确定。

同时，可以根据这三点对学习系统进行改良。

七、优化验证测试

可以判断出改进学习算法与改进得分函数哪个更重要。

八、端到端的学习

在数据量十分丰富的问题上，端到端系统往往很奏效，但它并不总是一个很好的选择。

什么时候选择流水线？数据可用性，人物简单性。

流水线例子：

假设你正在构建一个暹罗猫检测器。下面是一个纯粹的端到端架构：

与此相反，你可以分成两个步骤来形成流水线：

与仅仅使用标签 0/1 来训练一个纯粹的端到端分类器相比，流水线中的两个组件——猫咪检测器和猫种类分类器——似乎更容易进行学习，而且需要更少的数据。（其中每个组件都是一个相对 “简单” 的功能，因此只需要从少量的数据中学习。）

端到端例子：

这体现了深度学习的高速变化趋势：当你有正确的（输入，输出）标签对的时候，有时可以进行端到端学习，即使输出是一个句子、图像、音频，或者其它的比一个数字更丰富的输出形式。

九、根据组件进行误差分析

非正式：查看每个组件的输出，并看看是否可以决定哪个部分出错了。

正式：对每个组件提供“完美”输入，再判断误差。比如，猫检测器输出了边界框将猫咪切断，用手动标记的边界框替换猫检测器的输出，然后判断猫种类分类器。

组件误差分析与人类水平对比

1、在检测汽车时，汽车检测组件与人类水平表现相差多少？

2、在检测行人时，行人检测组件与人类水平表现相差多少？

3、整个系统的性能与人类表现相差多少？在这里，人类水平的表现假定：人类必须仅根据前两个流水线组件的输出（而不是访问摄像机图像）来规划汽车的路径。

ML 流水线存在缺陷

如果你认为，即使每个组件都具有人类级别的性能（请记住，你要与被给予与组件相同输入的人类进行比较），流水线整体上也不会达到人类水平的性能，则表明流水线有缺陷，应该重新设计。

在前一章中，我们提出了这三个部分组件的表现是否达到人类水平的问题。假设所有三个问题的答案都是肯定的，也即是说：

汽车检测部件（大概）是人类级别的性能，用于从摄像机图像中检测汽车。

行人检测组件（大概）是人类级别的性能，用于从摄像机图像中检测行人。

与仅根据前两个流水线组件的输出（而不是访问摄像机图像）规划汽车路径的人相比，路径规划组件的性能处于类似水平。

然而，你的自动驾驶汽车的整体性能远远低于人类水平。即，能够访问摄像机图像的人可以为汽车规划出明显更好的路径。据此你能得出什么结论？唯一可能的结论是ML 流水线存在缺陷。

十、小技巧_扩大训练集

1、不同分布的训练集和开发/测试集，然后给不同的数据加上不同的权重

例如，训练集包含了互联网图像+移动应用图像，而开发/测试集只包含移动应用图像。只有当你怀疑这些额外的数据（网络图像）与开发/测试集分布不一致，或者额外的数据规模比与相同分布的开发/测试集（手机图像）数据规模大得多时，这种类型的权重加权才需要。

此时需要四个数据子集：

训练集：这是算法将学习的数据（例如，互联网图像+移动应用图像）。这并不需要我们从与真正关心的相同分布（开发/测试集分布）的数据中提取。

训练开发集：这些数据来自与训练集相同的分布（例如，互联网图像+移动应用图像）。它通常比训练集要小；它只需要足够大到来评估和跟踪我们的学习算法的进展。

开发集：这是从与测试集相同分布的数据中抽取出来的，它反映了我们最终关心的数据的分布（例如，移动应用图像） 。

测试集：这是从与开发集相同分布的数据中抽取出来的（例如，移动应用图像）。

有了这四个独立的数据集，你现在可以评估：

训练误差，对训练集进行评估。

该算法能够泛化到与训练集相同分布数据的能力，并对训练开发集进行评估。

算法在你实际关心的任务上的性能，通过对开发集/测试集评估。

评估解读：

假设在猫咪检测任务中，人类获得了近乎完美的性能（0%误差），因此最优错误率大约为 0%。

1% 的训练集误差；5% 的训练开发集误差；5% 的开发集误差——>高方差

10% 的训练集误差；11% 的训练开发集误差；12% 的开发集误差——>高偏差

10% 的训练集误差；11% 的训练开发集误差；20% 的开发集误差——>高偏差、高方差

2、人工合成数据

当你在合成数据时，请考虑一下你是否真的在合成一组具有代表性的样本。尽量避免给出合成数据的属性，防止过拟合。

附件1：中英文对照

机器学习：machine learning

神经网络：NN，neural network

梯度下降：gradient descent

层：layer

隐藏元：hidden units

参数：parameters

标签：label

线性回归：linear regression

对数几率回归/逻辑回归：logistic regression

数据可用性：data availability

计算规模：computational scale

性能表现：performance

学习算法：learning algo

小型：small

中型：medium

大型：large

训练集：training set

开发集：development set

留出交叉验证集：hold-out cross validation set

测试集：test set

分类器：classifier

泛化：generalize

实际分布：actual distribution

过拟合：overfit

过拟合：overfitting

欠拟合：underfitting

基准测试：benchmark

单值评估指标：single-number evaluation metric

查准率/精确度：Precision

查全率/召回率：Recall

想法：idea

代码：code

实验：experiment

误差分析：Error Analysis

被误标注：mislabeled

偏差：bias

方差：variance

学习曲线：Learning curves

优化验证测试：Optimization Verification test

附件2：定义及公式

1、F分数

 分数（  Score），又称平衡F分数（balanced F Score），它被定义为精确率和召回率的调和平均数。

更一般的，我们定义

  分数为

  、 、 分数在统计学中也得到大量的应用

  分数中，召回率的权重高于准确率

 分数中，准确率的权重高于召回率

2、G分数

F分数是准确率和召回率的调和平均数，G分数被定义为准确率和召回率的几何平均数。