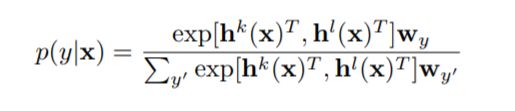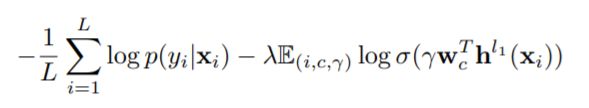文献阅读——Revisiting Semi-Supervised Learning with Graph Embeddings
文献阅读——Revisiting Semi-Supervised Learning with Graph Embeddings
1 背景介绍
半监督学习的目标是利用未标记的数据来提升模型的效果。大量的半监督学习算法共同优化两个训练时的目标函数。包括基于已标记数据的监督学习损失和基于已标记和未标记数据的半监督学习的损失。基于图的半监督学习的损失以一种对于监督学习的损失和图的拉普拉斯正则化项的加权求和的形式来定义。图的拉普拉斯正则化是基于相邻节点之间拥有相同标签的结构的假设来定义的。图的拉普拉斯正则化因为约束了标签在图结构中的一致性,所以该正则化项是有效的。
最近已经提出来的无监督的表示学习方法是学习到用来预测上下文分布的表示。例如,一个词的编码可以用来预测其相邻的上下文。或一个节点的编码可以用来预测图中的相邻节点。通过上下文分布训练出来的节点编码可以被用来提升相关任务的模型效果。例如,通过语言模型训练的词的表示可以被应用的语音识别,分块和命名实体识别。
在本文中,我们考虑的不是词的编码,而是图的编码。已经存在的一些结果反映了图编码在图中的节点分类任务上是有效的。例如,在社交网络中用户行为的预测。然而,图编码的学习经常依赖于一个监督学习的任务。并且不能够利用到在具体任务中的标签信息。因此在某些场景下的图编码是对图拉普拉斯正则的一种补充,这种补充不能够生成有用的信息,并且不能够完全的利用到编码好的图的结构信息。
我们的主要工作是合并了在图的半监督学习的几种学习技巧。我们提出了一个新的半监督的学习框架,Planetoid。一个实例的编码被训练来进行对于类别标签的预测和上下文的预测。然后,我们在分类器的隐层结构中拼接了两个部分的向量,并且将结果送入到softmax中来进行预测。
因为这种编码的学习是基于图结构的,第一种学习方式为转导推理,这种方式意味着我们只能够预测在训练的时候看到的例子。在很多的场景下面,需要使用到第二种学习方式,称为归纳推理,这种学习机制可以用来预测在训练的时候没有在图中出现的例子。为了解决这个问题,我们对我们的框架进行了对于适应于归纳推理的变形。这里我们以一个参数化的函数来定义编码,该函数以特征向量作为输入。例如,编码可以被看做是一个神经网络的隐层。
为了展示我们的模型的有效性。我们使用了五个数据集来完成三个任务,包括文本分类,远距离监督的实体抽取,和实体分类。我们转导推理方法的效果相比于第二名提升了18.7%,并且在准确率上平均提升了7.8%。我们归纳推理和转导推理的最好效果提升了8.5%,并且平均提升了4.1%。
2 相关工作
2.1 半监督学习
令L和U是已标记和未标记的实例。令 X 1 : L X_{1:L} X1:L和 X L + 1 : L + U X_{L+1:L+U} XL+1:L+U表示的是已标记数据和未标记数据的特征向量。其中标签 Y 1 : L Y_{1:L} Y1:L已经给出。基于已标记和未标记的数据,半监督学习的问题被定义为去学习一个分类器 f : x − > y f:x->y f:x−>y。这里有两种学习的范式。包括转导推理和归纳推理。转导推理的目标是将分类器 f f f应用到在训练时被使用当时没有被标记的数据上面。分类器不适用于在训练过程中没有发现的数据。例如:转导支持向量机(TSVM),其基于低维分隔假设来最大化未标记数据直接的距离。而低维分布假设指的是一个好的决策是依赖于一个分隔的特征空间的。另一个方面,归纳推理hi为了学习到一个参数化的分类器 f f f来对于为发现的数据来进行应用。
2.2 基于图的半监督学习
除了已经标记的数据和没有标记的数据,一个图也可以被表示成一个 ( L + U ) ∗ ( L + U ) (L+U)*(L+U) (L+U)∗(L+U)的矩阵A。在矩阵A中,也存在一些半监督的学习方法。首先,在矩阵A中的某一个元素 a i j a_{ij} aij揭示了两个实例i和j之间的相似性。其中两个实例之间可以已标记的实例,也可以是未标记的实例。图矩阵A可以被定义为描述不同实例之间的距离的矩阵,也可以通过一些额外的数据来进行定义。例如,一个知识图谱或者文献引用组成的网络结构。在本文中,图结构是明确被给出的,并且图代表了一些在特征向量中不存在的信息。例如,图的边反应了两个文献之间的引用关系,而不是基于词袋模型的生成的向量表示之间的距离。
基于图的半监督学习是基于相邻节点之间存在相同标签的假设的。一般的,基于图的半监督学习的损失函数定义如下所示:
∑ i = 1 L l ( y i , f ( x i ) ) + λ ∑ a i j ∣ ∣ f ( x i ) − f ( x j ) ∣ ∣ 2 = ∑ i = 1 L l ( y i , f ( x i ) ) + λ f T △ f − − − − − − − − − ( 1 ) ∑_{i=1}^Ll(y_i,f(x_i))+λ∑a_{ij}||f(x_i)-f(x_j)||^2=∑_{i=1}^Ll(y_i,f(x_i))+λf^T△f ---------(1) i=1∑Ll(yi,f(xi))+λ∑aij∣∣f(xi)−f(xj)∣∣2=i=1∑Ll(yi,f(xi))+λfT△f−−−−−−−−−(1)
在上述的损失函数中,可以分成两个部分来看,第一个部分是监督学习的损失,而 l ( . ) l(.) l(.)表示的是具体的损失函数的定义,这种损失函数可以是对数损失,可以是平方损失,可以铰链损失等等函数。第二项是图的拉普拉斯正则化,其表示的是一个大的惩罚项,当具有相同标签的节点被预测为不同的标签的时候,可以利用这一项来施加一个大的惩罚项。图的拉普拉斯矩阵被定义为 △ △ △。其中 △ = A − D △=A-D △=A−D,D是一个对角矩阵,其中的每一个元素表示为 d i i = ∑ j a i j d_{ii} = ∑_ja_{ij} dii=∑jaij,λ是一个常数项。为了简单起见,这里我们只考虑监督学习的损失,以及半监督学习的惩罚项,这里没有给出参数的正则化。大量的基于图的半监督学习定义的损失函数都是基于公式1 的变形。比如,标签传播算法强制分类器 f f f的分类结果和已标记的数据 Y 1 : L Y_{1:L} Y1:L的标签对应。也就是说f对于图中未标记的数据是一个标签查询表,并且可以获得相似形式的解决方案。算法“学习局部和全局的一致性”定义了损失函数l是一个平方损失,并且将f视为一个标签查找表,其不强制f和已标记的数据标签统一。MAD算法是一个标签传播的变形,通过在RKHS空间内将函数f进行参数化,并且将 l l l定义为平方损失或者铰链损失。因为 f f f是参数化,所以主要的正则化是归纳推理,并且可以和自然的应用到处理为发现的实例中去。
半监督的编码扩展了公式1中的正则化项成 ∑ i , j a i j ∣ ∣ g ( x i ) − g ( x j ) ∣ ∣ 2 ∑_{i,j}a_{ij}||g(x_i)-g(x_j)||^2 ∑i,jaij∣∣g(xi)−g(xj)∣∣2,其中g表示的是对于实例的编码表示,这种编码的具体形式可以是神经网络中的输出标签,隐藏层或辅助编码。通过将正则化函数f扩展成g,这种方法对于神经网络增加了更强的约束。迭代分类算法(ICA)使用了一个局部分类器,这种分类器以邻居节点的标签作为输入,并且在估计局部分类器和预测新标签之间增加一个迭代过程。
2.3 编码学习
在关于图编码学习的问题上,已经有了大量的研究。一个概率生成模型被提出,用来在一个图中生成边。一个聚类方法被提出来学习在一个社交网络中学习隐藏的社交状态来预测社交标签。
更近一些,大量的基于SkipGram(一种softmax的变形)的编码学习方式被提出。给定一个实例和其上下文,Skipgram的目标是用来最小化在使用实例的编码来预测上下文的时候所产生的损失。一般情况下,令 { ( i , c ) } \{(i,c)\} {(i,c)}一对实例i和上下文c的集合。其损失函数可以被定义为如下的形式:
− ∑ ( i , c ) l o g ( c ∣ i ) = − ∑ ( i , c ) ( w c T e i − l o g ∑ c ′ ∈ C e x p ( w c ′ T e i ) ) − − − − − − − − − − − ( 2 ) -∑_{(i,c)}log(c|i)=-∑_{(i,c)}(w_c^Te_i-log∑_{c'∈C}exp(w_{c'}^Te_i))-----------(2) −(i,c)∑log(c∣i)=−(i,c)∑(wcTei−logc′∈C∑exp(wc′Tei))−−−−−−−−−−−(2)
其中C是所有可能的上下文的集合。 w ′ w' w′是Skipgram的参数, e i e_i ei是实例i的编码表示。Skipgram第一次被引入是用来学习词向量的表示,比如众所周知的Word2Vec,对于每一个训练对 ( i , c ) (i,c) (i,c),实例i是需要进行进行词汇编码估计的实例,上下文c是实例i周围的一个固定窗口大小的词汇。上下文空间C是语料库的词表。然后,Skipgram被用来学习图的表示。DeepWalk使用一个节点的编码来预测图中的上下文,其中上下文是通过随机游走来实现的。更具体的,每一个每一个训练对 ( i , c ) (i,c) (i,c),实例i是当前需要进行编码的估计的节点。上下文C是在一个固定窗口大小下,通过随机游走来发现的相邻节点。上下文空间C表示的是图中的所有节点。LINE算法通过一阶节点和二阶节点来使得模型拥有更加丰富的上下文空间。
尽管类似于Skipgram的模型收到了很多的关注,但是也存在很多其他的方法,比如TransE模型在图中增加了关系来学习实体的表示。自编码器被用于通过聚类来学习图的编码。
2.4 对比
我们对比了我们的模型和其他的方法在半监督学习和编码学习的表现。不同于我们的模型,一般的图拉普拉斯利用了标签的正则化信息,但是没有学习到向量的表示。半监督的编码方法学习使用使用神经网络来学习编码表示,但是我们的方法与这种方法不同的地方在于不会强加正则化,我们使用编码来预测图中的上下文。图编码的方法将图结构形成编码,但是不同于我们的方法,这些方式是完全无监督的,并且在具体的任务中不会利用到标签的信息。更多的,上述的这些方法都是进行转导推理,其不能直接的对于在训练时未发现的结果进行生成结果。
3 通过图编码的半监督学习
通过上面章节的叙述,我们的方法的输入包括已标记的数据 X 1 : L , Y 1 : L X_{1:L},Y_{1:L} X1:L,Y1:L,以及未标记的数据 X L + 1 : L + U X_{L+1:L+U} XL+1:L+U,和一个表示图的矩阵A。每一个实例i有一个编码表示 e i e_i ei。
我们定义我们的框架是一个基于前向神经网络的结构。给定输入向量x, 神经网络的第k个隐层被表示成 h k h^k hk,其通过一个非线性的函数和前一层的输出来表示,具体为:
h k ( x ) = R e l u ( W k h k − 1 ( x ) + b k ) h^k(x)=Relu(W^kh^{k-1}(x) + b^k) hk(x)=Relu(Wkhk−1(x)+bk)
其中 W k W^k Wk和 b k b^k bk是第k层的参数,其中 h 0 ( x ) = x h^0(x)=x h0(x)=x。我们定义的损失函数也由两个部分组成,其基本表示为:
L s + L u L_s+L_u Ls+Lu
其中 L s L_s Ls是监督学习的损失,而 L u L_u Lu是对于预测图的上下文而产生的无监督的损失。下面,我们首先来介绍如何通过在图中的采样得到上下文,从而对无监督的损失进行定义,并且给出无监督损失的具体形式:
3.1 采样上下文
首先,我们定义的无监督的损失 L u L_u Lu是基于公式2的一个变形。给定一个图A,在我们的方法中,基本的思路是通过采样来生成实例i和上下文c。然后使用类似于公式2中的方式来通过对数函数来定义损失。我们首先来通过负采样的方法来描述 L u L_u Lu的基本形式,然后讨论如何对于实例和上下文对进行采样。
一般情况下,直接对于公式2进行优化是困难的,原因在于对于整个上下文空间的归一化。而负采样被引入来解决这个问题。这种采样通过对于负例的采样来近似的实现归一化项。在我们的问题中,我们从一个分布中采样 ( i , c , γ ) (i,c,γ) (i,c,γ),其中i和c表示实例和其上下文。 γ = + 1 γ=+1 γ=+1意味着(i,c)是一个正例对, γ = − 1 γ=-1 γ=−1表示是一个负例对。给定 ( i , c , γ ) (i,c,γ) (i,c,γ),我们来最小化对于输入对(i,c)的上下文预测二分类交叉熵损失。具体的函数定义如下:
− Ⅱ ( γ = 1 ) l o g σ ( w c T e i ) − Ⅱ ( γ = − 1 ) l o g σ ( − w c T e i ) -Ⅱ(γ=1)logσ(w_c^Te_i)-Ⅱ(γ=-1)logσ(-w_c^Te_i) −Ⅱ(γ=1)logσ(wcTei)−Ⅱ(γ=−1)logσ(−wcTei)
其中σ表示的是sigmiod函数,Ⅱ(.)是一个指示函数,输出的结果当参数为真时为1否则为0。因此,这种通过负采样的无监督损失定义为:
L u = − E ( i , c , γ ) l o g σ ( γ w c T e i ) − − − − − − − − − − − ( 3 ) L_{u}=-E_{(i,c,γ)}logσ(γw_c^Te_i)-----------(3) Lu=−E(i,c,γ)logσ(γwcTei)−−−−−−−−−−−(3)
其中分布 p ( i , c , γ ) p(i,c,γ) p(i,c,γ)是条件依赖于标签 y 1 : L y_{1:L} y1:L和图A。然而,因为我们的输入是固定的,所以在我们的叙述中取消了条件依赖。
我们现在直接使用一个采样过程来定义概率分布 p ( i , c , γ ) p(i,c,γ) p(i,c,γ),其过程如下面的算法所示:
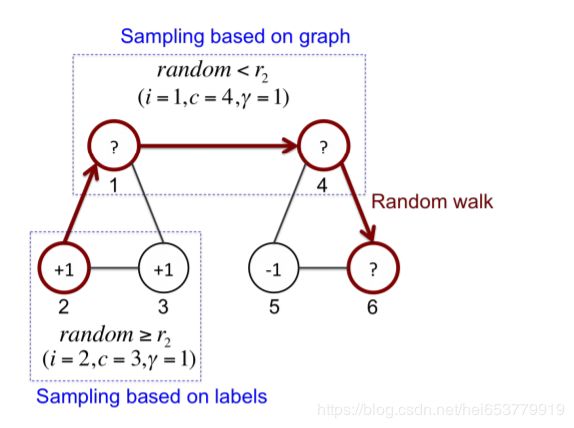
这里有两种上下文需要被采样,第一种是基于图A的上下文采样,其所表示的是编码的结构信息。第二种是基于标签的上下文信息的采样。,这里我们将标签信息注入到编码表示中。我们使用参数 r 1 ∈ ( 0 , 1 ) r_1∈(0,1) r1∈(0,1)来控制正例和负例的比例。并且使用 r 2 ∈ ( 0 , 1 ) r_2∈(0,1) r2∈(0,1)来控制两种类型的上下文的比例。
通过概率 r 2 r_2 r2,我们基于图A来进行采样上下文。首先,我们均匀采样出一个随机游走的序列S。更具体的,我们从集合1:L+U中均匀采样出第一个实例 S 1 S_1 S1,在给定前一个实例 S k − 1 = i S_{k-1}=i Sk−1=i的情况下,下一个实例 S k = j S_k=j Sk=j被采样的概率为 a i j ∑ j ′ = 1 L + U a i j ′ \frac{a_{ij}}{∑_{j'=1}^{L+U}a_{ij'}} ∑j′=1L+Uaij′aij。通过概率 r 1 r_1 r1,我们从一个集合 { ( S j , S k ) : ∣ j − k ∣ < d } \{(S_j,S_k):|j-k|
通过概率 ( 1 − r 2 ) (1-r2) (1−r2),我们基于标签来进行上下文的采样。正例对拥有相同的标签,负例对拥有不同的标签,这里只有实例1:L被采样。
我们随机游走的采样方式是基于Deepwalk上的,与他们的方式相反,我们的方式处理的是真实值的A,合并了负采样和通过概率 ( 1 − r 2 ) (1-r_2) (1−r2)的明确的采样来注入到监督学习的部分中。例如下面γ=1时的采样:
3.2 转导推理
在这一节中,我们提出了推断未标记数据 y L + 1 : L + U y_{L+1:L+U} yL+1:L+U的类别标签的方法,这种方法不会泛化到在训练的时候没有见过的数据。
转导推理的学习方法一般要比归纳推理方法的效果好,因为转导推理在训练的时候利用到了未标记的测试数据。
这里我们在输入向量X上使用一个K层的神经网络结构来获得结果 h k ( x ) h^k(x) hk(x),并且在编码上e使用一个l层的网络结构来获得 h l ( e ) h^l(e) hl(e),其结构如下图所示:

最后,这两个神经网络结构被拼接,然后送入到一个softmax层中来预测类别标签。更具体的,实例的标签为y的概率为:
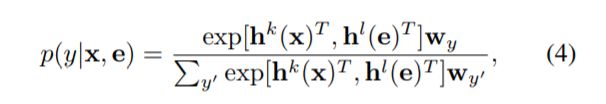
其中[.]表示的是两个行向量的拼接。 h T h^T hT表示向量h的转置。w表示模型的参数。与公式3相比,损失函数被定义为如下的形式:
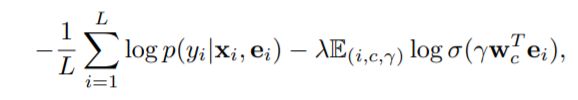
其中第一项是公式4定义的概率损失。λ表示的是一个常数项。第一项是对于类别预测的损失情况,第二项是对于上下文预测的损失情况。这种形式是转导推理的,因为标签y的预测依赖于编码e,而编码e的生成依赖于在训练过程中在图A中发现的实例。
其具体的训练算法描述如下:
3.3 归纳推理的基本形式
当我们考虑上述形式的转导推理的时候,在很多条件下,其可以被描述成一个能够预测在训练过程中未知实例的分类器。尤其是对于大规模的任务。例如,机器阅读系统经常会在Web上遇到没有发现过的实体,并且在半监督学习的过程使用整个Web是不现实的。然而,因为在图结构上学习到编码自然是转导推理生成的。其不能够直接的应用到归纳推理的上面。Perozzi通过重新训练编码来解决这个问题,这样既费时,又无法扩展。
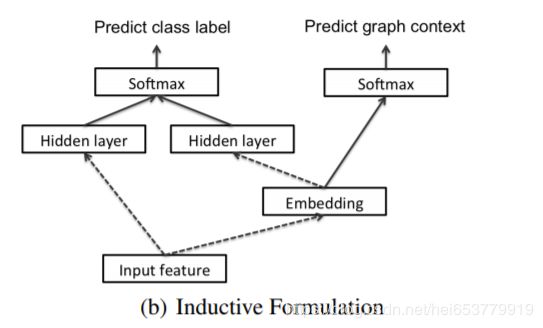
为了使得我们的方法能够进行归纳推理,对于标签y的预测应该依赖于输入的特征向量X。因此,我们定义编码e为一个参数化的关于输入x的函数。整体的处理流程如下:
与转导推理的形式类似,我们使用一个k层的网络来接收输入向量x,生成 h k ( x ) h^k(x) hk(x),然而,与使用一个“自由”的编码不同的是,我们使用一个 l 1 l_1 l1层的神经网络作用在输入x上,将其定义为编码 e = h l 1 ( x ) e=h^{l_1}(x) e=hl1(x)。另一方面,使用 l 2 l_2 l2层的网络结构来应用到 l 1 l_1 l1层网络的结果之上,即 h l 2 ( e ) = h l 2 ( h l 1 ( x ) ) h^{l_2}(e)=h^{l_2}(h^{l_1}(x)) hl2(e)=hl2(hl1(x)),这里将 h l ( x ) h^l(x) hl(x)定义为 l = l 1 + l 2 l=l_1+l_2 l=l1+l2。编码e可以被视为是一个隐藏层,相当于对于x的一个函数。
通过上面的定义形式,标签y仅仅依赖于输入的特征x,更具体的形式如下:
同时,通过使用 h l 1 ( x i ) h^{l_1}(x_i) hl1(xi)公式3中的 e i e_i ei,则对于归纳推理的损失函数的定义形式为:
4 实验
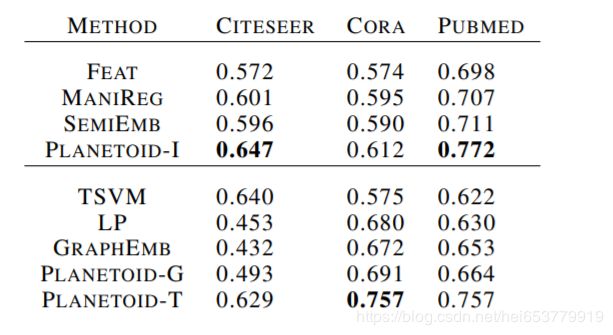
在本文中Planetoid-T和Planetoid-I分别表示的是我们的转导推理和归纳推理的两种方式。我们对比了标签传播方法,半监督的编码算法,多重调节算法(MainReg),TSVM算法以及图编码算法(GraphEmb),同时,我们定义了一个变形Planetoid—G,这个变形学习编码表示加入了标签预测和图上下文预测的任务,但是没有通过有用的特征向量作为输入。
4.1 文本分类任务
我们考虑,三种文本数据集,包括Citeseer,Cora和Pumed。每一个数据包含的是每一个文本的词表表示。我们以词袋的的表示作为特征向量。我们基于论文引用构建了图A。如果论文i引用了j,则我们设置 a i j = a j i = 1 a_{ij}=a_{ji}=1 aij=aji=1,分类目标是将每一篇文本归属于一个类别。我们为每一个类别随机采样了20个样本作为标记数据。1000个样本作为测试数据。剩下的作为未标记的数据。数据集的具体描述如下:
相同的数据被使用不同的方法进行分割,然后,我们计算平均准确率来进行比较。文本分类的结果如下:
4.2 远距离监督实体抽取
我们下一个考虑的数据集是DIEL数据集,其中DIEL数据集包括了预先抽取的在文本中的实体信息。以及将实体映射成坐标的坐标表。其目标是在给定特征向量和图结构之后,从文本中抽取医疗实体。
我们遵循了原始文献中对于实体抽取的试验设置,包括了在不同运行时刻对于数据的分割,实体概念的预处理和分割。并且计算了前k个召回作为评价指标。在下表中罗列了10次运行的平均结果。
5 参考
- Revisiting Semi-Supervised Learning with Graph Embeddings